同步定频微电网无通信二次调压策略

李海龙，赵艳雷，周国良，毕永健，刘 政，丁宏勋

(山东理工大学 电气与电子工程学院，山东 淄博 255000）

0 引言

分布式发电技术可有效解决能源问题[1]。但DG接入分散，大规模分布式电源单机入网会对大电网产生较大冲击，由DG组成微电网可解决上 述 问 题[2]。

微电网控制策略大多依赖通信，由于受地理位置或环境限制，部分微电网不具备通信条件[3]。文献[4]提出了一种基于卫星授时信号的同步定频电流 (Synchronous Fixed-Frequency Current，SFC）控制方法，微电网内的DG无需通信，完全即插即用。但孤岛模式下负荷变化会引起微电网电压波动，因此需要对同步定频微电网电压进行二次调节[5]。二次调压主要有两类控制方式，即集中式控制[6]和分布式控制[7]。集中式控制是由中央控制器采集DG信息并进行二次调整，对通信要求较高。分布式控制的DG只需通过本地控制器进行二次调整，无需通信或需要低速通信，且鲁棒性较强，是目前二次调压研究的热点。文献[8]提出了一种同步定频微电网并网/孤岛切换策略，但未涉及同步定频微电网电压二次调节。文献[9]提出了一种自适应动态调节下垂系数的调压方法，具有良好的动态性能，但是未考虑多台变换器并联的场景。文献[10]应用多智能体一致算法优化微电网电压，但需要一定的通信数据。文献[11]仅通过相邻微源间通信对孤岛微电网电压进行调节，降低了通信的要求，但需要冗余链路以提高系统稳定性，建设成本较高。文献[12]通过提升变换器输出基准电压提升母线电压，但未考虑负载变化的场景。文献[13]提出了基于二次无差调压的改进U-I下垂控制策略，可将电压恢复至额定电压，但并不能保证微网内各DG动作同步。文献[9]～[13]的调压方法不适用于多逆变器、多负载且无通信的同步定频微电网。

本文在SFC控制方法基础上，针对孤岛模式下由负荷变化引起的微电网电压波动较大的问题，基于就地电压信息提出了同步定频微电网调整下垂曲线的无通信二次调压策略，通过调整DG输出电压，使得负载端电压始终在设定的范围内。同时为保证DG动作的同步性，提出了基于卫星授时信号的下垂曲线调整方法，使微电网内各DG同步调整下垂曲线。

1 同步定频微电网基本原理

同步定频微电网即微网内分布式电源以卫星授 时 信 号 秒 脉 冲(One Pulse Per Second，1PPS）为基准，各DG输出的电流相位相同且频率固定[4]。同步定频微电网如图1所示。

图1 同步定频微电网示意图Fig.1 Schematic diagram of synchronous fixed-frequency microgrid

图中：DG为分布式电源；PCC为公共连接点；DG1～DGn通过一个并网开关与大电网连接。并网模式下，各DG采用有功、无功给定控制(PQ控制），输出的有功和无功功率固定；孤岛模式下，DG采用下垂控制策略，DG输出电压和电流随负荷变化，故本文针对孤岛模式下的微电网研究二次调压策略。

2 同步定频微电网无通信二次调压策略

2.1 同步定频微电网DG控制系统结构

同步定频微电网一般由多个DG系统和负载组成，以单个DG系统为例，其控制结构如图2所示。

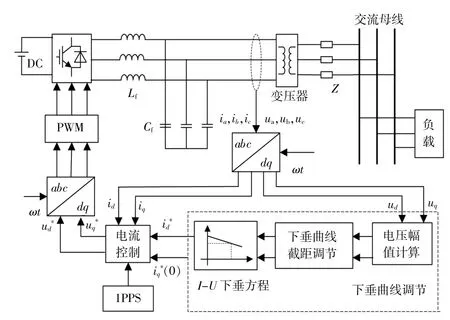
图2 DG控制系统结构Fig.2 DG control system structure

图中：Lf和Cf分别为滤波电感和电容；Z为线路 阻 抗；ia，ib，ic为DG输 出 电 流；ua，ub，uc为DG输出 电 压；id，iq和ud，uq分 别 为DG输 出 电 流 和 输 出电压在旋转坐标系下的dq分量；ud，uq经下垂方程计算出电流参考值id*，iq*设置为零，使得三相输出电流相位与卫星授时信号同步且幅值等于id*。由电流环计算出交流侧参考电压dq分量ud*和uq*，结合参考角度 ωt，转换成abc三相静止坐标系下的三相调制电压信号指令值，实现对DG输出电压的调节。

DG电流环控制结构如图3所示。

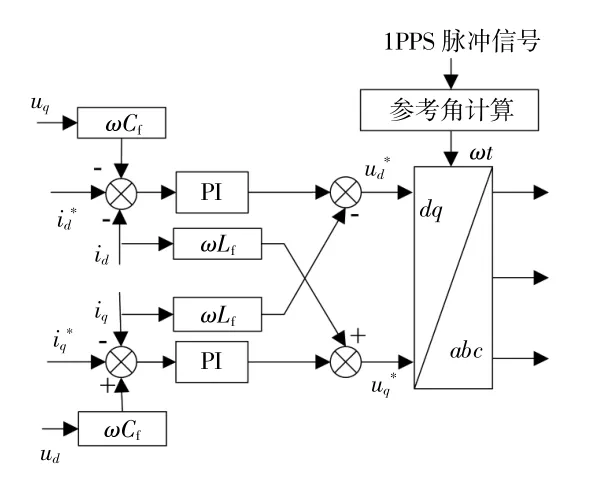
图3 DG电流环控制结构Fig.3 DG current loop control structure

由图3可得电流环控制结构方程为

式中：Kp，Ki分别为比例和积分系数。

电流环PI调节器比例环节可减少DG输出电流与参考电流id*的偏差，积分环节可消除DG输出电流与id*的静差，实现对id*的无差跟踪。目前对于电流环的研究设计已十分充分[14]，本文对I-U下垂控制策略及二次调压原理展开分析。

2.2 同步定频微电网二次调压原理

本文在SFC控制的基础上采用I-U下垂控制策略，其方程为

式中：I为输出电流；Iref为参考电流(也称下垂曲线截距）；K为下垂系数；U为输出电压有效值。

当DG输出功率增加时，DG输出电流增加，输出电压减小；当DG输出功率减小时，DG输出电流减小，输出电压增加。因此，当负荷变化导致电压跌落或电压过高时，需要对各DG进行二次调压，以满足电能质量的要求。

本文根据DG输出电压幅值调节下垂曲线截距，对下垂曲线进行平移调整，其中DG输出电压幅值，平移下垂曲线法如图4所示。

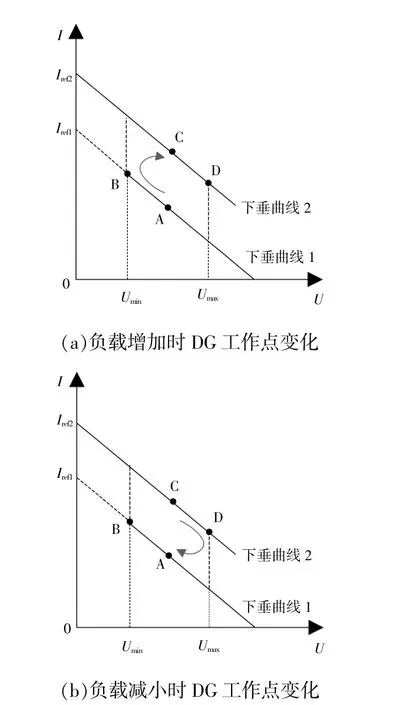
图4 负载功率改变时DG工作点变化Fig.4 Variation diagram of DG operating point when load power changes

图中：Iref1，Iref2分别为下垂曲线1(低档下垂曲线）和下垂曲线2(高档下垂曲线）的截距；B点电压和D点电压分别为最小电压阈值Umin和最大电压阈值Umax。

为防止电压振荡，设置了调整死区。负载增加时，初始状态DG工作点为A点，增加负载后，DG工作点转移到了B点，达到最小电压阈值，此时DG下垂曲线调整为高档下垂曲线，工作点转移到C点，且C点电压小于D点电压。负载减小时，初始状态DG工作点为C点，此时减小负载，DG工作点转移到D点，达到最大电压阈值，则DG下垂曲线调整为低档下垂曲线，工作点又回到了A点，且A点电压大于B点电压。

2.3 下垂曲线截距和电压阈值计算设计

2.3.1下垂曲线截距计算设计

忽略线路阻抗的影响，对下垂曲线截距进行设计，此处采用标幺值进行计算。设定电压最小阈值为Umin，最大阈值为Umax。在低档下垂曲线中，当DG输出电压达到Umin时需要进行调压，此时DG输出电流达到最大值Imax，DG输出功率最大。调压后DG输出电压要小于Umax，否则会出现电压振荡。假定调压后DG输出电压达到Umax，则令：

由式(3）即可计算出Iref2，上述计算忽略了调压后DG输出功率略微增加的情况。

本文所采用的I-U低档下垂曲线为I=11-10U，设 定Umin为0.95 p.u.，Umax为1.05 p.u.，由 式(3）可 得Iref2=11.85 p.u.，考 虑 到 死 区，取Iref2=11.83 p.u.，即高档下垂曲线为I=11.83-10U。

2.3.2电压阈值计算设计

由于不同线路的阻抗不同，需要针对不同线路中DG的电压阈值进行设计。采用I-U下垂控制时，DG输出电压电流是由下垂曲线和代表线路电气特性的曲线共同决定的[15]，线路特性曲线方程为

式中：Zn，Un，In分别为第n台DG所在线路的线路阻抗、DG输出电压和输出电流；UPCC为公共连接点电压(公共母线电压）。

以两台DG为例，线路阻抗与DG输出电压电流关系如图5所示。

图5 线路阻抗与DG输出电压电流关系Fig.5 Relationship between line impedance and DG output voltage and current

图5中Z2>Z1，当DG设置同样下垂曲线时，I1>I2，U1＜U2，为 保 证DG1和DG2灵 敏 度 相 同，需要调整其电压阈值。

联 立 式(2），(4）可 得：

忽略负载与公共母线之间的线路阻抗，则负载电压Uload=UPCC，根据需求设定Uload取值范围后，即可由式(5）计算出不同线路中的DG最小/最大电压阈值。

2.4 二次调压对DG输出功率的影响

在微电网中，各DG并联运行向公共连接点供电，DG并联等效电路如图6所示。

图6 DG并联等效电路图Fig.6 DG parallel equivalent circuit diagram

图 中：Un∠φn为 第n(n=1，2）台DG的 输 出 电压；UPCC∠0 °为公共 连接点电压；In为第n台DG的输出电流；Iload为负载端电流；Zn=Rn+jXn为线路阻抗；Zload为微电网内负荷。

根据图6可知，第n台DG输出的有功功率Pn、无 功 功 率Qn分 别 为

低压微电网中线路呈阻性，线路中的感性分量可忽略。与此同时，DG与PCC点相角差 φn接近 于0(φn＜0），则sin φn≈φn，cos φn≈1。故 结 合 式(6）可得DG输出有功和无功功率为

由式(7）可知，当DG从低档下垂曲线切换到高档下垂曲线时，由于调压作用，DG输出有功功率和无功功率均增加。而调压前后两台DG下垂参数始终一致。因此，本文所提二次调压策略并不会对功率分配造成较大影响，DG功率分配差额主要来源于线路阻抗差异。

3 DG下垂曲线同步调整方法

在无通信的环境下，由于没有中央控制器，各DG只能采集就地信息，无法得知其他DG运行状态，当增加/减小负载时，如果各DG动作不同步，则可能出现各DG工作在不同下垂曲线的情况，引起较大的功率不平衡。为解决此问题，本文提出基于卫星授时信号的下垂曲线同步调整方法。各DG以1PPS秒脉冲信号为基准，在接收到秒脉冲信号时，每隔一段时间检测一次当前电压，如果电压低于最小电压阈值或者高于最大电压阈值，则调整下垂曲线。本文将检测时间间隔设置为10 ms，即每半个周期检测一次当前电压，不管何时增加/减小负载，各DG总是在相同的时刻检测并调整下垂曲线，使得各DG动作同步。电压检测点位置如图7所示。

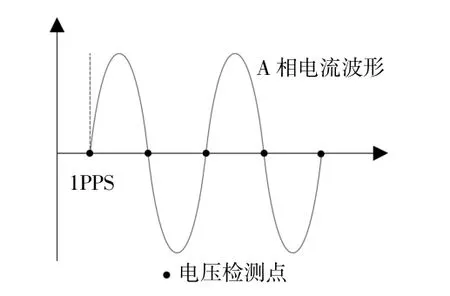
图7 电压检测点相对于1PPS信号位置Fig.7 Voltage detection point relative to 1PPS signal position diagram

由图7可知，DG的A相电流上升沿和1PPS秒脉冲信号计算出的参考相位一致，同时DG每次接收到1PPS脉冲信号都将重新计时，以提高计时的准确性。初始状态下，DG下垂曲线为低档下垂曲线，DG调整下垂曲线过程如图8所示。

图8 DG调整下垂曲线过程Fig.8 Process of DG adjustment droop curve

4 仿真验证

在Matlab/Simulink中搭建微电网模型，系统一次接线图如图9所示。仿真参数如表1所示。

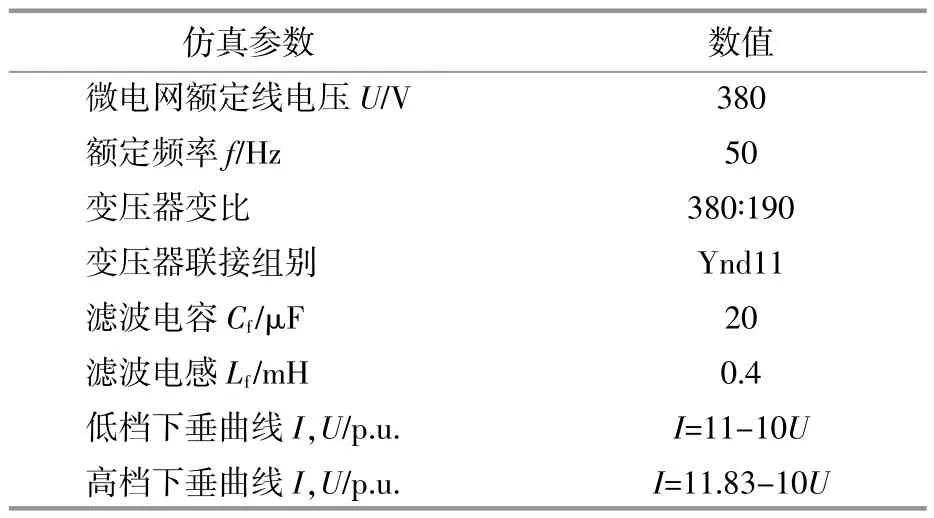
表1 实验仿真参数Table 1 Experimental simulation parameters

图9 微电网仿真及实验一次接线图Fig.9 Microgrid simulation and experiment primary wiring diagram

仿真模型包括两台DG，DG1，DG2容量比为1∶1，两台DG采用相同的下垂曲线参数，DG基准相电流为16 A，基相电压为110 V。为模拟实际情况中线路阻抗不相等的场景，本文设定线路阻抗Z1=(0.1+j0.01）Ω，Z2=(0.4+j0.04）Ω。

4.1 二次调压策略仿真验证

根据系统参数计算各DG电压阈值，计算最小/最大电压阈值时分别设定UPCC为209，231 V，由于线路中Xn较小可近似忽略，根据式(5）可得DG1最小/最大电压阈值为0.955/1.055 p.u.，DG2最小/最大电压阈值为0.969/1.067 p.u.。

初始状态下，两台DG下垂方程均为I=11-10U，负载功率为8 kW，此时负载电压幅值为538.7 V。在0.15 s时，增加8 kW负载功率，即总的负载功率为16 kW，在0.3 s时，再降低8 kW负载功率。

仿真结果如图10所示。

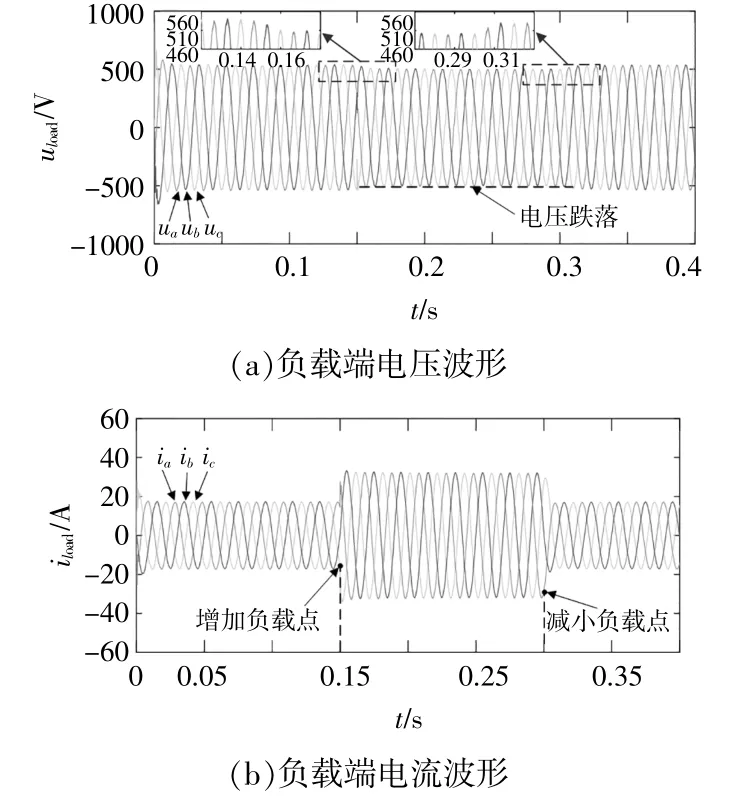
图10 无调压措施负载端电压电流波形Fig.10 Waveform of load terminal voltage and current without voltage regulation measures

由图10可知，在增加8 kW负载功率后，负载端电压降低，而负载电流增加，符合下垂方程特性，负载电压从538.7 V减小到了499.0 V，相比正常电压幅值537 V跌幅为7.08%，电压跌落较严重。由此可见，在没有调压措施的情况下，微电网电压随负荷波动较大，为保证微电网电能质量，需要对微电网电压进行二次调节。

图11为DG增加了调压措施的部分波形。设置初始负载功率为8 kW，在0.15 s时增加8 kW负载功率，在0.3 s时再降低8 kW负载功率。

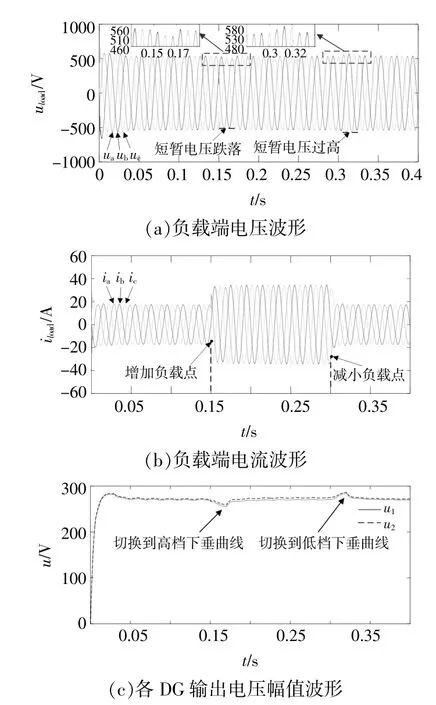
图11 有调压措施微电网波形Fig.11 Waveform of microgrid with voltage regulating measures

表2 为负载功率变化时负载端详细参数。

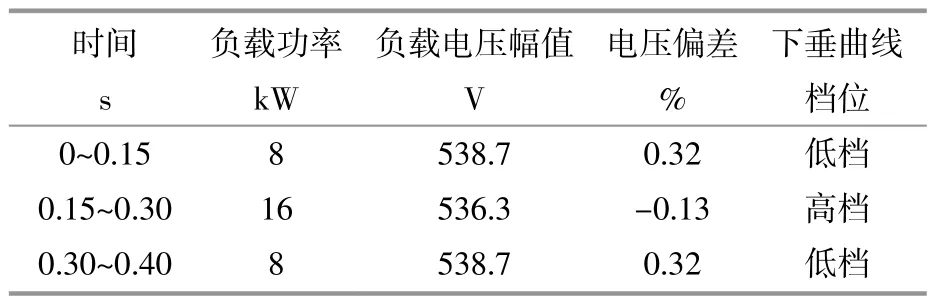
表2 负载端详细参数Table 2 Detailed parameters of the load side

初始时负载端电压处于正常范围，在0.15 s增加负载后，由于下垂特性DG输出电压降低，导致负载端电压迅速跌落，此时DG检测到输出电压小于最小电压阈值，执行二次调压程序，将下垂曲线切换为高档，DG输出电压升高，使负载端电压迅速升高。同理，在0.3 s减小负载后，由于下垂特性DG输出电压升高且达到了最大电压阈值，再次执行二次调压程序，将下垂曲线切换回低档，DG输出电压降低，使负载端电压恢复正常。由表2可知，当负载功率为16 kW时，有调压措施时负载端电压偏差为-0.13%，与无调压措施时-7.08%的电压偏差相比有明显改善。由此可见，在有调压措施的情况下增加或减小负载，微电网电压波动较小，验证了二次调压策略的有效性。在调压过程中，由于DG每10 ms检测一次当前输出电压，因此输出电压幅值会有短暂的低于最小电压阈值或高于最大电压阈值的情况，属于正常现象。由图11(c）可知，在整个投切负载的过程中，DG1和DG2总是同步调整下垂曲线截距，验证了基于卫星授时信号的下垂曲线同步调整方法的有效性。

4.2 二次调压对DG输出功率影响仿真验证

将负载功率设置为4 kVar无功功率和12 kW有功功率，在低档下垂曲线和高档下垂曲线下，DG1和DG2的输出功率如图12所示。

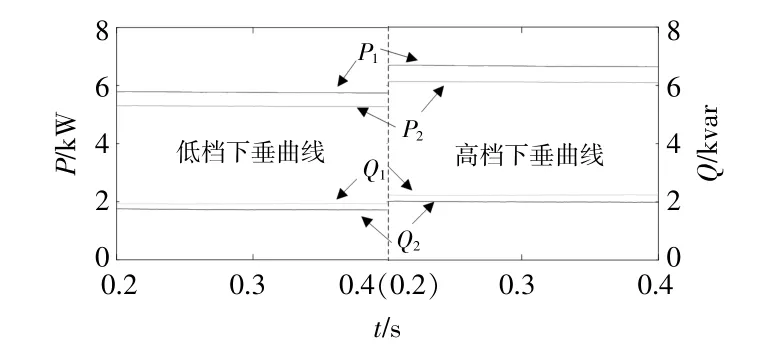
图12 不同下垂曲线下各DG输出功率Fig.12 Output power of each DG under different droop curves

图中：P1和Q1分别为DG1输出有功功率和无功功率；P2和Q2分别为DG2输出有功功率和无功功率。

DG1和DG2在低档和高档下垂曲线输出功率对比如表3所示。

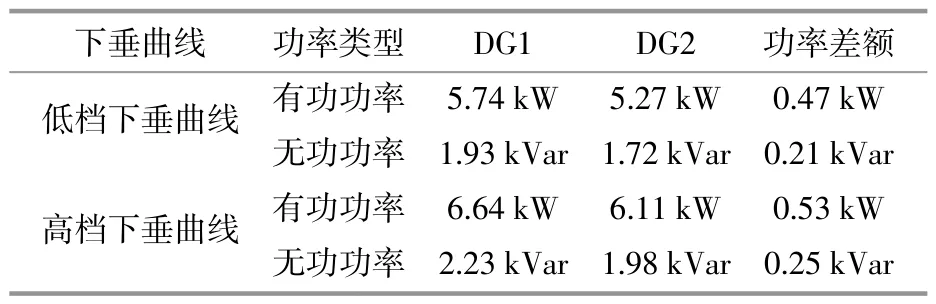
表3 各DG输出功率对比Table 3 Comparison of output power of each DG

由图12和表3可以看出，增加下垂曲线截距对功率分配影响较小，且可以提高DG输出功率，目前有较多DG功率平均分配方法，本文不再针对功率分配进行研究。

5 实验验证

为进一步验证所提策略有效性，搭建了包含两台30 kV•A逆变器和两台20 kV•A负载的微电网，通过DL850E型录波仪采集记录数据。系统一次接线如图9。图13为实验平台照片。实验室内DG1，DG2和负载距离较近，可近似忽略线路阻抗影响，因此DG1与DG2采用相同的下垂参数和电压阈值，I-U下垂曲线低档为I=11-10U，高档为I=11.83-10U，最小电压阈值标幺值为0.96 p.u.，最大电压阈值标幺值为1.06 p.u.，为方便查看实验波形，将实验中同步检测电压时间间隔设定为20 ms。

图13 实验平台照片Fig.13 Photo of the experimental platform

实验中负载1和负载2均为6 kW，初始时仅投入负载1，一段时间后投入负载2，随后再切除负载2。图14为实验波形。

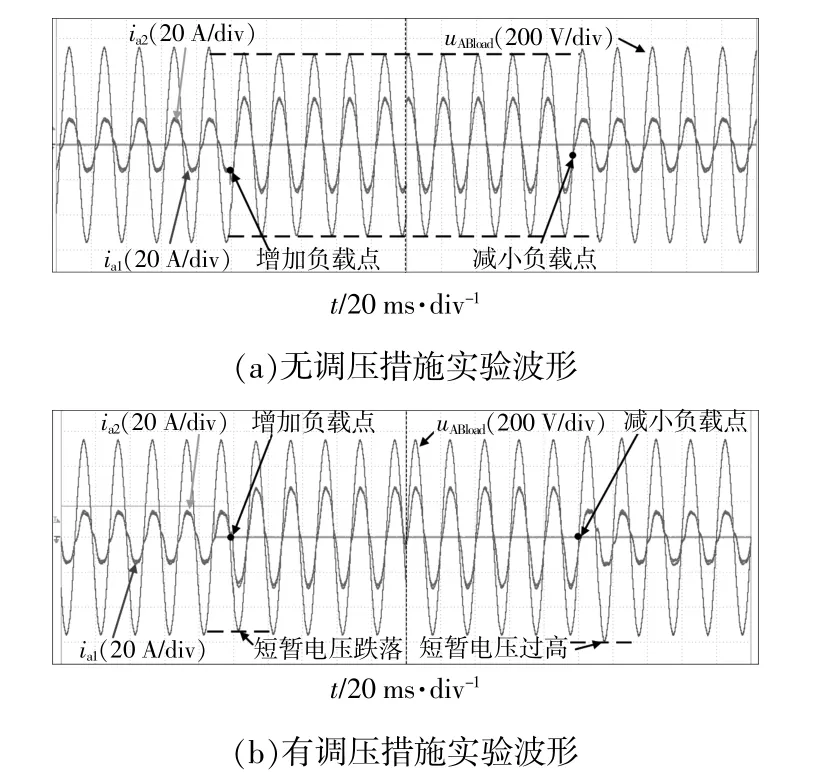
图14 实验波形Fig.14 Experimental waveform

图14(a）为无调压措施实验波形，左侧为投入负载2时实验波形，右侧为切除负载2时实验波形。投入负载2前，负载端电压幅值为546 V，投入负载2后，负载端电压下降到509 V。增加负载会导致负载端电压降低，与仿真现象一致，因此需要进行二次调压。图14(b）为有调压措施实验波形，左侧为投入负载2时实验波形，投入负载2之前负载端电压幅值为546 V，投入负载2后，负载端电压出现短暂的电压下降，DG输出电压达到最小电压阈值，DG切换到高档下垂曲线，使DG输出电压升高，负载端电压恢复至543 V。右侧为切除负载2时实验波形，在切除负载2后，负载端电压出现短暂的电压过高，DG输出电压达到最大电压阈值，DG切换回低档下垂曲线，负载端电压恢复至546 V。实验结果与仿真结果一致，验证了本文所提二次调压策略的有效性。

6 结论

针对同步定频微电网在孤岛运行模式时，负荷变化会引起电压波动，本文提出了一种微电网电压二次调节方法，该方法在无通信的情况下通过检测就地电压幅值调整下垂曲线，实现对同步定频微电网电压的二次调节。基于卫星授时信号提出一种同步调整下垂曲线的方法，使各DG同步调整下垂曲线。本文所提二次调压策略对DG功率分配影响较小，且可以提高DG输出功率。仿真和实验结果表明，在增加/减少负载功率后，本文提出的无通信二次调压方法可以使负载端电压始终处于设定的电压阈值范围内，验证了二次调压策略的有效性。本文所提调压策略易于实施，调压过程迅速且无需通信，有较高的实用价值。