考虑峰谷分时电价的风储联合发电系统跟踪风电计划出力控制策略

2023-12-22罗隆福阳同光杨京渝陈长青

可再生能源 2023年12期

彭丽，罗隆福，阳同光，杨京渝，陈长青

(1.湖南大学电气与信息工程学院，湖南长沙 410000；2.湖南城市学院智慧城市能源感知与边缘计算湖南省重点实验室，湖南益阳 413000）

0 引言

风电是实现能源可持续发展和“双碳”目标的有效途径[1]。然而，风电功率的波动性和间歇性给电网的安全稳定运行带来了巨大的冲击和影响[2]，[3]。依据风电短期预测功率制定发电计划，能够在一定程度上缓解风电并网对系统的冲击，但短期预测功率与实际风电功率之间仍然存在较大偏差[4]。储能技术能够有效弥补风力发电的弊端，为提高风电场跟踪计划出力的精度创造了条件[5]。但只以提高跟踪调度计划出力为单一的工作模式，风电场储能运营主体效益不明显。

国内、外学者在BESS提高跟踪风电计划出力控制策略方面开展了深入的分析和研究[6]～[9]，主要分为事后实时断面控制和实时超前优化控制两大类[10]。事后实时断面控制主要是通过BESS来实时修正各时刻实际风电功率与计划值之间的偏差。文献[11]对BESS的运行控制策略展开研究，提出了BESS分组控制策略，兼顾了风电计划出力跟踪和BESS使用寿命。文献[12]提出了在线滚动优化和有功实时控制相结合的协调优化控制策略，降低了储能充放电转换次数，提高了风储联合系统跟踪计划出力能力。但事后的实时断面控制大多采用及时调节方法，并未考虑BESS未来SOC的变化情况，易出现电池过充、过放以及容量得不到充分利用等问题，影响了风储系统控制效果与经济性。实时超前优化控制主要是结合超短期风电功率预测实现具有前瞻性的超前控制。文献[13]构建了以降低储能SOC波动范围与充放电深度为目标的优化模型。结合风电功率预测信息，提出了采用实时滚动优化方法跟踪发电计划的控制策略，实现了BESS容量的充分利用。文献[14]以储能下令次数最少为优化目标，利用超短期功率预测实现考核周期内的超前滚动优化，提高了风电跟踪计划精度。在此基础上，文献[10]利用卡尔曼滤波算法对超短期风电功率预测数据进行分钟级的增强处理，提升了功率预测的细粒度，并结合超前滚动优化控制策略，实现了风储系统考核电量与储能寿命的精准优化。但实时超前优化控制的效果过度依赖于风电功率的预测精度。

以上研究为风储系统跟踪调度计划出力控制策略提供了丰富的理论支撑，取得了一定的成果。但鲜有文献在满足跟踪风电计划出力的前提下，从提高BESS经济效益的角度制定控制策略。本文综合考虑提高风储系统跟踪计划出力能力以及收益，提出了一种基于MPC和双层模糊控制的BESS跟踪风电计划出力控制策略。首先，基于MPC方法建立了BESS跟踪风力发电计划控制模型，设计了以并网功率与计划出力偏差、BESS剩余容量偏离理想值为最小的目标函数；然后，为了在提高跟踪调度计划能力的同时，提高BESS的峰谷套利收益，提出了一种双层模糊控制策略。当并网功率超过跟踪允许偏差带时，通过采用第一层模糊控制实时调整目标函数中的权重系数，以获得最佳跟踪效果。当并网功在跟踪允许偏差带内时，为进一步提高BESS收益，结合SOC和峰谷分时电价，采用第二层模糊控制规则，对BESS的充放电功率进行修正；最后，以某风电场实际数据为例，在风储联合发电系统实验平台上进行了测试，验证了所提控制策略的可行性和优越性。

1 风储联合发电系统

风储联合发电系统的拓扑结构见图1。该系统主要由风电场、储能站、升压变压器、变流器及能量管理系统等组成，通过输电线路连接至电网。

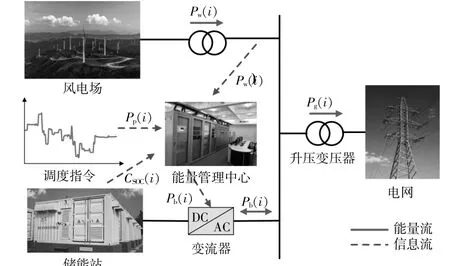
图1 风储联合发电系统结构示意图Fig.1 Structure drawing of wind storage combined power generation system

在电网实际调度运行时，依据风电功率预测值制定发电计划值PP(i）。通过合理的控制策略计算BESS的充放电功率Pb(i），补偿实际风电功率Pw(i）与计划值PP(i）之间的差值，最终得到风储联合系统并网功率Pg(i）。风储联合发电系统功率平衡方程和储能能量状态迭代方程分别为

式中：CSOC(i）为i时刻ESS剩余容量；Tc和Crated分别为BESS控制周期和额定容量；η为BESS转换效率，本文取值为90%。

根据相关规定[15]，中短期预测准确率应大于等于80%，可建立发电计划跟踪允许偏差带，即实际功率和计划出力曲线之间的允许误差范围，其表达式为

式中：Pu(i），Pd(i）分别为允许偏差带上、下限；δ为偏差带设置系数；PP(i）为i时刻风电功率计划值。

根据上述分析，可求得目标功率值Pa(i）为

2 基于MPC储能系统控制模型

基于上述功率平衡方程、能量状态迭代方程，创建MPC系统模型。同时，结合目标功率值，兼顾储能寿命和跟踪能力，建立MPC滚动优化目标函数和约束条件，并将其转化为二次规划问题进行求解。

2.1 基于MPC系统模型

MPC是一类考虑有限时间域内开环最优控制的方法，采用滚动规划、提前控制的思想[16]～[22]。其控制原理如图2所示。

图2 跟踪风电计划出力的MPC框图Fig.2 MPC block diagram for tracking planned wind power output

根据式(1），(2）并结合叠加定理，选取并网功率Pg(i）和BESS剩余容量CSOC(i）构成状态变量，即x(i）=[Pg(i），CSOC(i）]T。以ESS出力Pb(i）作为控制变量，即u(i）=Pb(i）。风电功率Pw(i）作为输入变量，即r(i）=Pw(i）。则风储联合发电系统的状态空间方程为

根据MPC原理，结合状态空间方程(7），可求得未来i+k时刻的输出量为

取u(i+1）为i+1时刻的BESS输出功率，更新并网功率和SOC，进入下一时刻优化过程求解。

2.2 目标函数与约束条件

为延长BESS使用寿命，在满足跟踪计划的同时降低储能输出，通过将储能SOC变化引入优化过程，使SOC趋向于理想值，以提高BESS对未来风电功率变化的适应能力。因此，本文建立以并网功率与计划出力偏差、BESS剩余容量偏离理想值最小的目标函数。

式中：Cideal为BESS剩余容量理想值，取0.5倍额定容量；α，β为权重系数，α+β=1。

在MPC滚动优化目标函数的同时，还需满足以下充放电功率和SOC约束。

①BESS功率约束

式中：Prated为BESS额定功率。

②BESS容量约束

式中：SOCmin，SOCmax分别为BESS荷电状态的下限和上限。

3 基于双层模糊控制的BESS输出功率修正

本文定义MPC滚动优化目标函数，该函数兼顾了并网功率与计划出力之间的偏差、BESS剩余容量偏离理想值为最小的多目标优化。在此基础上，通过设计双层模糊控制器，在不同情况下通过修正BESS的充放电功率，确保计划出力跟踪、BESS收益与安全工作目标的多任务执行。

3.1 权重系数分析

从目标函数(10）可以看出，BESS输出功率受权重系数α的控制。α取值越大，BESS剩余容量越接近理想值，但跟踪计划曲线效果越差；相反，若 α取值越小，则跟踪效果越好，但可能会使SOC越限。因此，本文采用以下方法对 α的取值进行实时动态调整。①在i+1时刻，当实际风电功率值超过计划偏差带上限或下限时，应尽量保证风储联合出力在跟踪允许偏差带内，同时为避免SOC越限，采用第一层模糊控制器对权重系数α进行修正；②在i+1时刻，若实际风电功率预测值在跟踪允许偏差带内，为提高BESS的峰谷套利收益，同时避免SOC越限，采用第二层模糊控制对BESS充放电功率进行修正。

3.2 第一层模糊控制

由于BESS容量和充放电功率具有一定范围，若SOC和充放电功率超过其允许范围，将严重影响BESS使用寿命。基于此，采用第一层模糊控制器调节BESS的充放电功率，维持SOC在允许的工作范围内。将SOC和BESS输出功率作为模糊控制的输入变量，分别定义为X1和X2，权重系数α作为模糊控制器的输出变量。

模糊控制输入、输出隶属函数如图3所示。

图3 第一层模糊控制器隶属度函数Fig.3 Membership function of the first layer fuzzy controller

模糊控制输入变量CSOC(i）论域为[0，1]，模糊集为{VS，S，M，B，VB}，依次表示 “小值”、“偏小值”、“适中”、“偏大值”、“大值”。变量Pb(i）的论域为[-1，1]，模糊集为{NB，NS，Z，PS，PB}，依次表示“负大值”、“负小值”、“零”、“正小值”、“正大值”。模糊控制输出变量 α论域为[0，1]，模糊集为{VS，S，M，B，VB}，依次表示“小值”、“偏小值”、“适中”、“偏大值”、“大值”。

模糊控制规则如表1所示。

表1 第一层模糊控制规则Table 1 Fuzzy control rules of first layer

3.3 第二层模糊控制

为提高BESS峰谷套利收益，对BESS充放电功率再次进行修正，即：

式中：Pb(i+1|i）为i+1时刻BESS修正后的运行指令；Δk为修正系数，取值为[-1，1]。

从式(13）可以看出，BESS充放电功率的修正主要取决于Δk的选取。因此，采用第二层模糊控制对 Δk进行动态调整来修正BESS的充放电功率。将峰谷电价和SOC作为模糊控制的输入变量，分别定义为X3和X4。将BESS的充放电修正系数Δk作为模糊控制的输出变量。模糊控制输入、输出隶属函数如图4所示。

图4 第二层模糊控制器隶属度函数Fig.4 Membership function of the second layer fuzzy controller

模糊控制输入变量X3的模糊集为{L，M，H}，依次表示 “小值”、“适中”、“大值”，论域为[-1，1]。模糊控制输入变量X4的模糊集为{NB，NS，ZE，PS，PB}，依次表示 “极小值”、“偏小值”、“适中”、“偏大值”、“极大值”，论域为[0，1]。模糊控制的输出变量Δk的模糊集为{NB，NM，NS，NV，ZO，PV，PS，PM，PB}，论域为[-1，1]。

基于SOC和峰谷电价的BESS充放电功率修正模糊规则如表2所示。

表2 模糊控制规则Table 2 Fuzzy control rules

采用上述模糊控制规则的BESS充放电功率修正方法，一方面可以避免BESS过度充放电，另一方面可以利用BESS对能量的时空平移能力，提高风电场收益。综上所述，本文所提控制策略的具体流程如图5所示。

图5 控制流程图Fig.5 Control flow chart

4 算例仿真分析

算例场景为一地区某装机容量为50 MW的风电场实测风功率数据，在风储联合发电系统综合控制实验平台上进行了仿真，如图6所示。实验平台拓扑结构、系统功能及二次参数等完全参照实际工程设计，平台主要由储能站EMS系统、风机SCADA系统、无功补偿监控系统、升压站综合自动化系统、AGC/AVC一体化智能监控系统等组成。

图6 控制流程图Fig.6 Simulation experiment platform

风电场和BESS的参数设置如表3所示。

表3 仿真参数Table 3 Sinulation parameters

为说明本文所提控制策略(以下简称策略2）的可行性和优越性，采用以BESS出力最小为优化目标的传统MPC方法(以下简称策略1）进行对比。

4.1 评价指标

为评价控制策略的优劣，分别选取功率预测准确率[15]、最大跟踪偏差、BESS死区时间、BESS出力系数[16]以及峰谷套利收益[17]进行评价。

①功率预测准确率

式中：Pre为功率预测准确率；n为样本个数；Cap为风电场开机容量。

②最大跟踪偏差

式中：Pd.max为最大跟踪偏差。

③BESS死区时间

式中：Td为储能SOC达到设定安全阈值的时间，意味着BESS在一定程度上失去对计划曲线的跟踪能力。

④BESS出力系数

式中：Cb为ESS的输出能力，数值越小，出力能力越大；T为储能出力周期内的采样周期数。

⑤峰谷套利收益

BESS利用电网峰谷电价，通过“低储高发”获得收益。收益I的计算式为

式中：PD.t，PC.t分别为t时段BESS的充电、放电功率；Pprice.t为t时段电网的实时峰谷电价。

峰谷电价如表4所示。

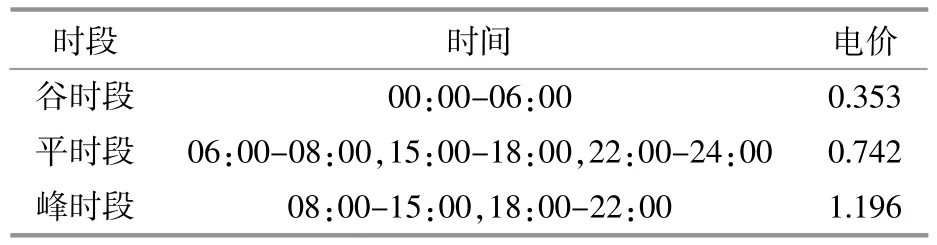
表4 电价Table 4 Electricity price元/(kW•h）

4.2 仿真结果分析

本文选取的风电功率实际值和计划值曲线如图7所示。风储联合出力曲线如图8所示。BESS SOC曲线如图9所示。BESS输出功率如图10所示。各图中采样周期均为5 min，1 d共计288个时间点(0：00-24：00）。表5为不同控制策略评价指标对比。

表5 评价指标对比Table 5 Evaluation index comparison

图7 实际风电功率与计划出力曲线Fig.7 Wind power actual output and planned output curve

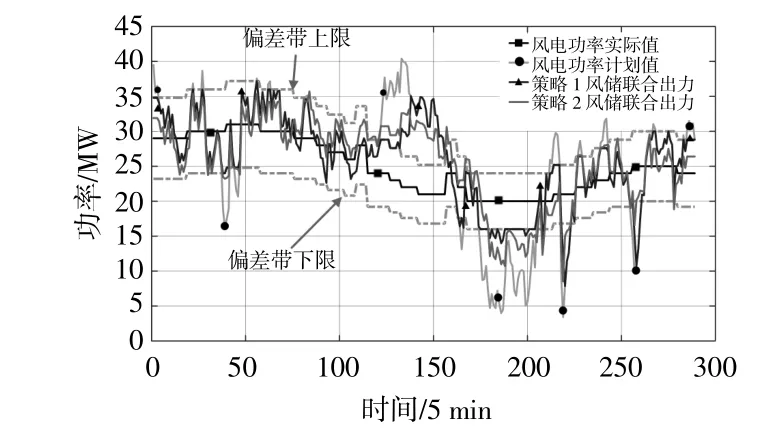
图8 不同控制策略风储联合出力曲线Fig.8 Combined output curves of wind-storage under different control strategy

图9 不同控制策略SOC变化曲线Fig.9 SOC variation curves for different control strategy

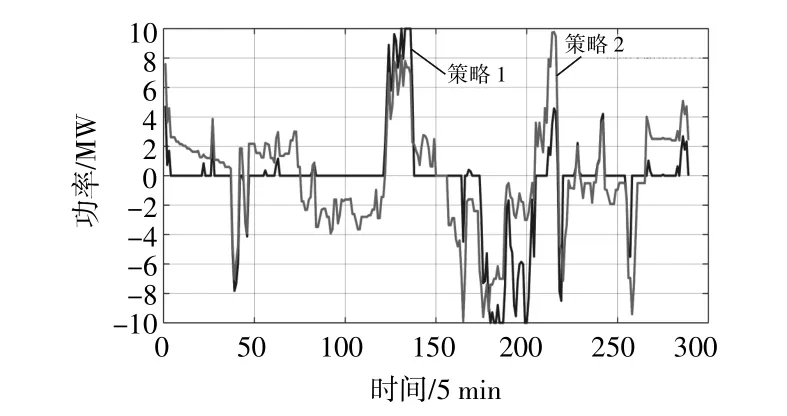
图10 不同策略BESS出力曲线Fig.10 BESS output curves for different control strategy

由图8可以看出，风电场加入BESS可以提高对风电计划曲线的跟踪能力，使并网功率满足允许偏差的时间大幅提升。结合表5可知，相比于未加储能，两种控制策略的预测准确率分别提高了9.65%和14.69%，最大跟踪偏差分别减少了4.13 MW和5.93 MW。相比于控制策略1，策略2预测准确率提高了4.6%，最大跟踪偏差减少了12.9%。从图9储能SOC变化曲线可以看出：在680～815 min，策略1 BESS处于高能量状态，造成其充电能力不足；在1 025～1 055 min，1 095～1 130 min和1 285～1 330 min 3个时间段，存在长期的低能量状态，BESS放电困难。从表5也可以看出，控制策略1 BESS总的越限时间长达255 min，出力系数为2.71；而控制策略2越限时间为0 min，出力系数为1.83。通过对上述数据分析可知，由于控制策略1未考虑当前SOC对未来跟踪能力的影响，当实际风电功率持续超过计划偏差带上限或下限时，会导致BESS越限，增大了BESS的出力系数，从而失去对风电计划出力的跟踪能力，降低预测准确率。而控制策略2采用了以BESS剩余容量偏离理想值最小为优化目标，当储能SOC偏高或者偏低时，通过第一层模糊控制器动态调整目标函数中的权重系数，将SOC逐步向理想值方向调整。因此，策略2增加了对未来跟踪能力的调节，减小了BESS出力系数，避免了BESS越限。相比于传统MPC控制方法，本文所提方法兼顾了对计划出力跟踪和剩余容量的调整，整体上跟踪效果更佳，验证了所提控制策略的优越性。

结合图7和图9可以看出，在250～600 min，风电功率实际值基本处于允许偏差带范围内。此时，控制策略1中BESS几乎不动作，BESS存在部分功率、容量的闲置，故其利用率低、经济效益不佳。因此，为充分利用BESS容量来提高风电场收益，当风电功率在允许偏差带内时，控制策略2综合考虑当前峰谷分时电价和SOC状态，采用第二层模糊控制对BESS的充放电功率进行修正，将谷时段的能量时移至峰时段，以此提高BESS的峰谷套利收益。结合图8～10可以看出，控制策略2在满足跟踪风电计划曲线和BESS不越限的同时，在谷时段尽量多充电，而峰时段多放电。如在360～420 min(谷时段），通过第二层模糊控制器修正系数 Δk提高充电功率，SOC处于上升状态；在480～600 min(峰时段），控制BESS进行放电，SOC处于下降状态；在1 320～1 440 min(平时段），第二层模糊控制器综合考虑当前峰谷分时电价和SOC状态，使SOC曲线逐步向0.5的方向调整，而控制策略1的SOC依旧处于较低值。对全天各时段内BESS的充放电电量进行统计得出：策略1在谷时段释放电量0.793 5 MW•h，在平时段释放电量10.657 MW•h，在峰时段吸收电量4.871 MW•h；策略2在谷时段吸收电量11.975 8 MW•h，在平时段释放电量3.838 1 MW•h，在峰时段释放电量10.120 5 MW•h。以此可知，控制策略1不仅未将谷时段电量时移至峰时段，反而在谷时段和峰时段分别释放和吸收了电量。相比于控制策略1，控制策略2提高了谷时段风电消纳，从表5也可以看出，控制策略2多增加峰谷套利收益8 362.6元。

5 结束语

为提高风储联合发电系统的可调度性和收益，本文提出了一种基于模型预测控制和双层模糊控制的BESS跟踪风电计划出力控制策略。所提控制策略兼顾跟踪风电计划出力和BESS出力能力，能够在提高风电功率计划跟踪能力的同时，显著地减小BESS进入死区的时间。与传统MPC控制方法相比，预测准确率提高了4.6%，BESS出力能力提高了32.5%。设计的双层模糊控制策略综合考虑了计划出力跟踪、BESS收益与安全工作目标的多任务执行。相比于传统MPC控制方法，大幅减少了BESS越限时间，充分利用了BESS容量，在提高风电并网能力的同时，也获得了良好的峰谷套利收益。