基于Vine-Copula和拟蒙特卡罗法的可再生能源电力现货市场风险度量模型

郑 伟，王宣定，梁志远，甘倍瑜，龚昭宇，赖晓文

(1.广东电力交易中心有限责任公司，广东 广州 510080；2.北京清能互联科技有限公司，北京 100080）

0 引言

目前，深度参与电力现货交易的可再生能源通常为水电，风电、光伏等仅在甘肃、蒙西等进入了现货市场。“碳达峰、碳中和”战略目标的背景下，急需评估可再生能源参与电力现货市场的风险。对电价风险的度量通常基于VaR、条件风险价 值(Conditional Value at Risk，CVaR）、期 望 损 失(Expected Shortfall，ES）等[1]，常 见 的 计 算VaR模型方法有历史模拟法、分析法和蒙特卡罗(Monte Carlo，MC）法[2]～[4]。

当前，风电、光伏等可再生能源未广泛、深度参与现货市场，直接采用历史数据度量风险的传统方法(如直接采用电力现货市场中可再生能源的收益）难以应用；另一方面，与传统能源不同，可再生能源出力具有间歇性和波动性，直接采用VaR值作为风险度量值不能反映可再生能源出力不确定性带来的风险。因此，本文基于可再生能源的有效出力和VaR模型，设计了可再生能源的风险度量指标。针对国内电力现货市场数据量少的情况，本文采用MC法计算VaR，假定市场满足一定的模型并通过生成大量数据进行风险度量值的计算[4]。但传统MC法产生的随机数为伪随机数，其群聚效应会影响数据的准确值，导致传统MC法收敛速度过慢，通常需要大量样本才能得到较小误差的结果[5]。因此，本文对传统MC法的VaR模型进行了改进，采用拟蒙特卡罗(Quasi-Monte Carlo，QMC）法，通过生成均匀分布的样本序列，提高模型收敛速度。QMC法在金融计算[6]、期权定价[7]等领域得到了广泛应用，在电力领域也已应用于 可靠 性评 估[8]、潮流 计 算[9]、电压稳定计算[10]等，其快速收敛的特性能允许VaR进行高频计算。在QMC法所模拟的市场模型中，本文建立了市场因子到风险水平的映射关系。市场因子之间的相关性通过Copula函数进行描述[11]，在电力领域中，Copula函数也通常在风速模型中描述自变量的相关性研究[12]，[13]。但对Copula函数的应用通常是刻画二元变量之间的相关性，影响市场风险的市场因子通常有两个以上，包括市场边际条件、电网阻塞情况、市场申报水平等因素，传统二元Copula函数并不能满足电力市场风险因子相关性的描述需求。为此，本文创新性地采用Vine Copula函数进行多个电力市场因子的相关性描述。

本文所提出的模型，为可再生能源未深度参与市场环境下的风险度量提出了解决方案，通过对风险场景进行定义，逐个风险场景、考虑可再生能源有效出力进行风险度量；克服了电力现货市场样本量不足的问题，创新性地采用Vine Copula函数考虑多个电力市场因子间的相关性，拟合市场因子对电价水平的映射关系，通过QMC法生成低差异序列计算VaR，改进了传统MC法计算VaR收敛慢的缺陷。最后结合南方(以广东起步）电力现货市场2020年8月的结算试运行数据和同期海上风电、光伏的仿真数据，对模型进行了算例分析。

1 理论基础

1.1 Copula函数

Copula函数用于分离多变量之间的随机性和耦合性，随机性由变量各自的边缘分布衡量，耦合性则由Copula函数衡量。

假设X1，X2，…，XN为电力市场中N个市场因子，其 各 自 的 边 缘 分 布 分 别 为F1(x1），F2(x2），…，FN(xN），则 存 在Copula函 数C(•），使 得：

对于二元分布模型，运用较多的Copula函数主要为椭圆族Copula函数和阿基米德族Copula函数两类[14]。对于多元联合分布模型，通常采用高斯Copula或Vine Copula刻画多个变量之间的耦合性，其中：高斯Copula把随机变量之间的相关性描述为高斯分布[15]；Vine Copula比高斯Copula更能表征多元联合分布的多样性，建立随机变量之间的树结构，通过二元Copula函数考虑两两节点之间的相依关系[16]。常见的树结构为R-vine(Regular Vine）。

①T1为 具 有N1(1，2，…，n）个 节 点 和E1条 边的树。

②对 于i=2，…，n-1，Ti为 具 有Ni=Ei-1个 节 点和Ei条边的树。

③对 于i=2，…，n-1，{a，b}∊Ei，其 中，a={a1，a2}，b={b1，b2}，且 有#(a∩b）=1，#表 示 集 合 的 势。

即，R-vine每一层的树，其边均在下一层的树变为节点，若两条边共享了一个节点，则下一层的这两条边变成的节点由新的边连接。C-Vine(Canonical Vine）和D-Vine(Drawable Vine）为RVine的两种特殊结构，两者在金融领域有较多应用[17]。C-vine每层树均有一个中心节点，适合存在一个变量与其他变量相关性较强的情况，树结构如图1所示。D-vine每层树均为线性，树结构如图2所示。此前，国内电力市场因子之间的相关性并未有相关研究，无法判断高斯Copula的适用性，因此本文通过Vine-Copula描述多个市场因子之间的相关性。

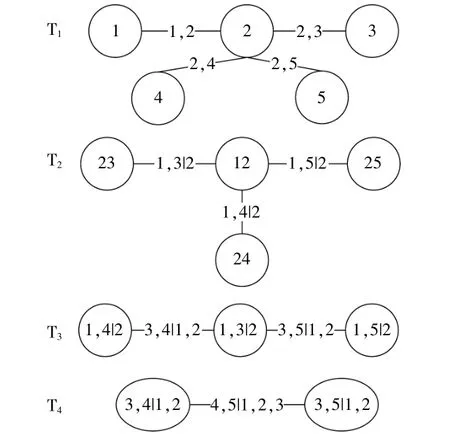
图1 五节点C-Vine结构图Fig.1 Five-node C-vine structure diagram

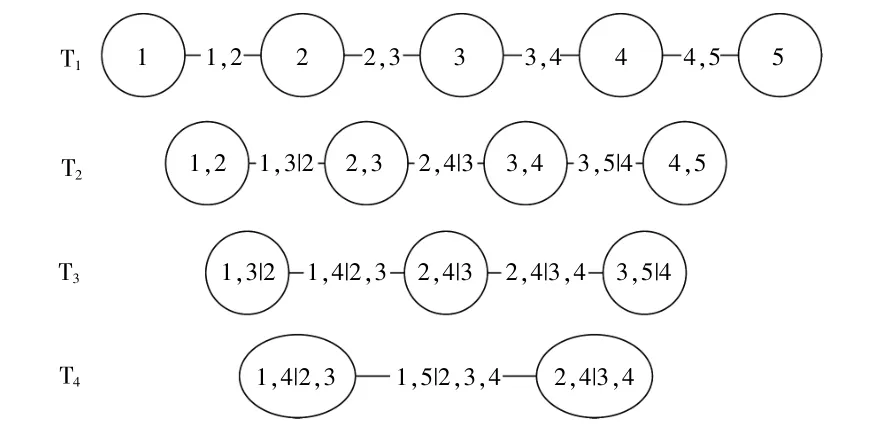
图2 五节点D-Vine结构图Fig.2 Five-node D-vine structure diagram

1.2 拟蒙特卡罗法

电力市场中的风险量化形式为

式 中：f(X）为 电 力 市 场 的 风 险 度 量 函 数；X=[x1，x2，…，xs]为各个市场因子；Ω为f(X）的s维积分空间。

MC法是对X进行均匀抽样的过程，根据强大数定理，MC法的估计误差近似于正态分布，均值为0(MC法的估计为无偏估计），标准差表达式为 [18]

式中：σf为f(X）的样本方差；n为样本数目。

要减少MC法的误差可以增大样本数目或减少样本方差，但样本数目的增加会随之带来计算成本的增加；QMC法是通过构建低差异序列(Low Discrepancy Sequences）代替传统MC法中的伪随机数序列，以达到减少样本方差的目的。低差异序列克服了伪随机数列的群集性，分布更均匀，在随机 点(x，y）=[0，1]2的 采 样 空 间，内 低 差 异 序 列 与 伪随机数列散点图对比如图3所示。

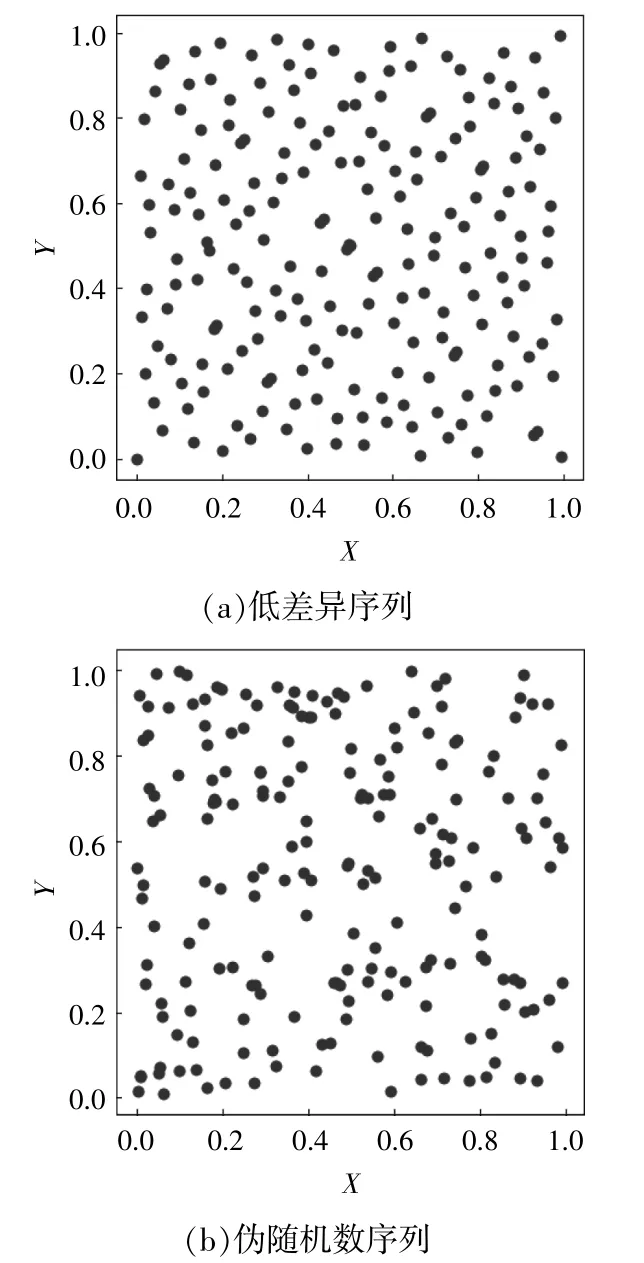
图3 低差异序列与伪随机数列散点图对比Fig.3 Comparison of low difference sequence and pseudorandom number sequence

QMC法中的低差异序列比MC法中的伪随机序列 σf更小，达到同样的精度只需要更少的样本数目n[19]。常见的低差异序列有Ver der Courput序 列、Halton序 列、Sobol序 列 等[20]，其 中Sobol序列以2为底数进行计算，可以进行位运算，计算效率高，因此在数值积分、数理金融等金融工程领域得到了广泛应用[21]。

在方法的效用分析上，通常对MC法和QMC法的收敛性进行检验，评价标准为方差系数[8]等。定义电力市场风险度量的方差系数为

式中：σ，μ分别为QMC样本的样本方差与样本均值。

随着样本数量的增大，MC法和QMC法的结果逐步收敛，方差系数将会下降并稳定在一定水平。

2 基于Vine-Copula和拟蒙特卡罗法的可再生能源风险度量模型

2.1 市场因子分析

市场因子是指在市场环境中影响电力市场价格风险的因素。文献[21]所列出的市场因子包括电力市场结构、市场化程度、网络结构、市场规则、市场装机、负荷、报价策略、历史电价、一次能源价格等。对于市场因子的选择并非一成不变的，而应当根据不同市场实际情况选择影响程度高的数个市场因子。另一方面，考虑到所建立的模型方能为市场主体所用，指导市场主体规避价格风险，应当采用市场公开数据。

基于广东电力现货市场的信息披露情况，结合本文算例中样本的时间窗口，为提高模型灵敏度，不考虑时间窗口内变动范围较小的市场因子，本文选取了下列3个市场因子。

①市场竞价空间

市场竞价空间指的是在国内电力市场双轨制下，扣除市场出清边际条件，在集中出清市场中参与竞价的部分电量。市场出清的边际条件通常包括非市场化机组的出力计划、外送电计划、地方电源出力计划等。对于广东电力现货市场，市场竞价空间s为

式 中：d为 统 调 预 测 负 荷；swest，sH-M，slocal分 别 为 西 电东送计划电量、港澳联络线计划电量、地方电源出力计划。

②节点阻塞

采用阻塞度反映节点的阻塞情况，节点i的阻塞度ci为

式 中：pnode，i，pbase分 别 为 节 点i的 节 点 电 价 和 基 准 电价。

基准电价pbase选取系统边际出清价时，所计算得到的阻塞度ci最准确，但在国内电力现货市场环境下，系统边际出清价通常不是市场公开信息，因此在实证分析中，需选取一个价格每日波动小的节点，假定不容易受到阻塞的影响，以其节点电价作为基准电价pbase。

③量价指数

供需决定价格，而市场主体通过申报反映其供需意愿。对于国内电力现货市场仅发电侧申报的机制，影响市场价格的主要为发电侧的供给意愿和申报水平，可以通过量价指数b来进行量化，计算式为

式 中：pj，k，qj，k分 别 为 第k个 发 电 主 体 的 第j段 申报价格与申报量；J为申报段数目；K为市场中发电主体的数目。

在实际应用分析中，首先需对市场因子的历史数据进行模型分析，判断符合哪类分布；再通过分析得到的分布基于Vine-Copula进行数据生成。

2.2 考虑有效出力的可再生能源风险度量

衡量国内电力现货市场价格风险的VaR定义为，在假定的市场条件下，预计会在一定百分比的时间内呈现的电价水平，其表达式为

式中：P(•）为概率；p为电价水平；a为给定的置信水平；pVaR为给定置信水平a下的VaR，即在置信水平a下，电价水平大于等于pVaR。

假定可再生能源的出力分布是与市场价格无关的独立分布，则可再生能源参与市场的风险可以定义为

式中：Eβ为置信水平 β下的装机容量利用率；Rχ为置信水平χ下的可再生能源收益，且χ=α•β。

Eβ的计算式为

式中：C为机组的装机容量；Oβ为置信水平 β下的机组出力，即机组的有效出力。

2.3 模型概述

基于Vine-Copula和拟蒙特卡罗法的可再生能源电价风险度量模型如图4所示。

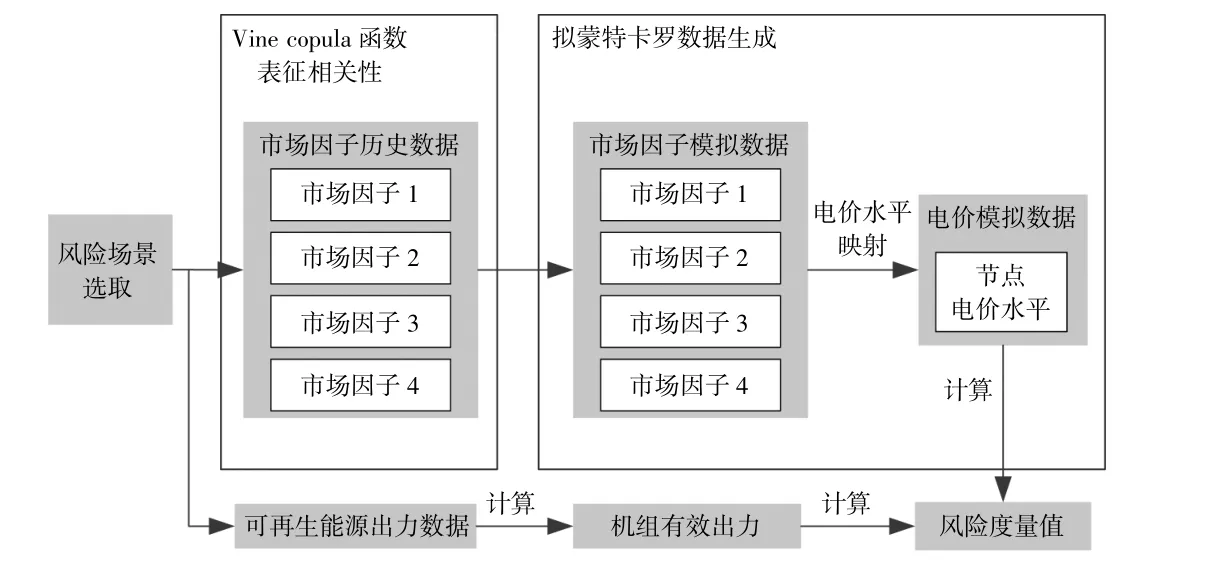
图4 风险度量模型Fig.4 Risk measurement model

模型步骤如下所示。

(1）风险场景选取

通过供需比紧张与否、上游能源价格高低、各类可再生发电的资源是否充足等指标定义不同的风险场景，在实际数据中，分别选取符合条件的市场因子历史数据和可再生能源出力数据，逐个风险场景进行后续的风险度量。

(2）Vine-Copula函数表征相关性

①对每一个市场因子进行分布分析，确定各自的边缘分布。

②建模Vine-Copula。本文算例有3个市场因子，其中C-vine和D-vine的结构是相同的，可直接采用D-vine进行市场因子相关性的表征。

③逐层建Vine-Copula。对每层的每对相邻点，先通过两个变量的kendall秩相关性系数求得不同Copula函数的参数，再将离散范数L2作为与经验Copula(Empirical Copula）的距离度量，选择与经验Copula最近的Copula函数作为最优Copula[22]。对每层的每对相邻边，求取条件累积分布函数并赋值给下一层相应的相邻点。

(3）QMC法数据生成

①通过已构造的Vine-Copula模型进行市场因子模拟数据生成。

②对市场因子的历史数据进行映射关系拟合。考虑到国内电力市场尚处于起步阶段，市场数据较少，而通过市场因子对电价水平的映射关系并非简单的线性关系，因此考虑采用支持向量回归(Support Vector Regression，SVR）的 方 法，以 描述市场因子对电价水平的映射关系。采用随机寻优和交叉验证进行超参数选取，选取拟合优度最高的参数组合作为模型参数。拟合优度衡量的是回归模型整体的拟合度。

③采用所拟合的映射关系生成电价模拟数据。

(4）风险度量计算

①通过出力数据得到机组有效出力。

②计算风险度量值。

3 算例分析

3.1 数据获取

本文选取2020年8月广东电力现货市场结算试运行日前市场的数据作为市场电价水平，并假定在这段时间内市场环境变化不大、属于同一个风险场景。由于8月1日的数据有缺失，仅对8月2-31日共30 d的数据进行分析，选取节点A作为算例分析的节点(由于节点信息敏感，节点名称均采用代号表示），计算风险度量值pVaR。

在该月结算试运行中，市场竞价空间、节点阻塞、量价指数3个市场因子，均能在市场公开信息中获取数据并计算而得。其中，市场主体的申报不分时，为全日每个时段的申报曲线，因此量价指数的数据颗粒度为1 d一个数据，因此对其余3个市场因子的数据颗粒度均求取每小时的算术均值，调整为1 d一个数据的颗粒度。节点电价水平也同样采用分时节点电价的算术均值作为本日的节点电价水平。

节点阻塞度的计算需选取价格每日波动小的节点，以其电价作为基准电价，定义节点n的电价波动率，描述该节点各小时的节点电价标准差的均值为

式 中：pn，h，d为n节 点d天h时 的 日 前 节 点 电 价，pˉn，h为n节点h时日前节点电价的D天均值；对于本实 例 分 析，D=30 d，H=24 h。

剔除平衡节点后，B节点的rSTD，n最 小，为34.37，将B节点的电价设定为基准电价。近年，广东电网的海上风电和光伏装机容量大幅上升，因此同期的可再生能源数据采用海上风电和光伏，假定其均以A节点价格结算。可再生能源部分采用仿真数据，分别以800 MW的Vestas V112 3000 Offshore型海上风电机组[23]和100 MW的光伏机组进行仿真，模型分别采用文献[24]和文献[25]的风机出力和光伏出力模型进行预测。实际的模型应用中应当采用真实的机组出力数据，针对特定的可再生能源机组进行风险度量。

3.2 数据分布分析与预处理

市场竞价空间、量价指数、A节点的阻塞度分布如图5所示。

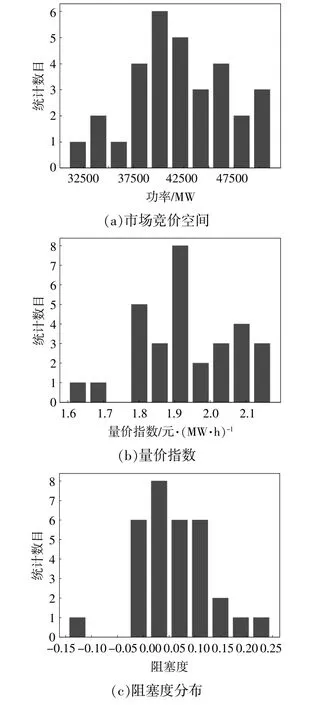
图5 市场因子分布Fig.5 Market factor distribution

考虑到样本数据量少，采用夏皮罗维尔克检验(Shapiro-Wilk test，S-W test）检 测 其 是 否 满 足正态分布，结果如表1所示。S-W检验的p值均大于0.05，3个市场因子的分布符合正态分布的假设，可以被接受。

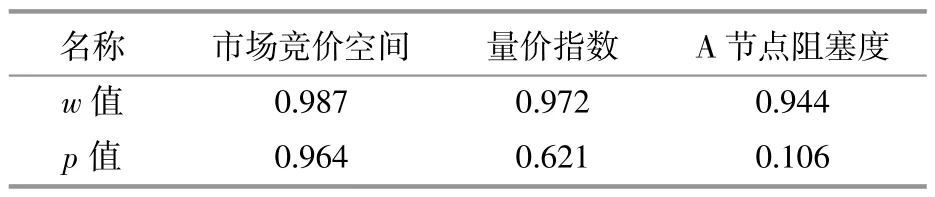
表1 夏皮罗维尔克检验结果Table 1 Result of shapiro-wilk test

不同的市场因子之间量纲不同，方便后续进行电价水平映射，对市场因子分别进行标准化为

式 中：y，y*分 别 为 原 数 据 和 标 准 化 后 的 数 据；yˉ，ystd分别为该市场因子数据的均值和总体标准差。

3.3 模型训练

对市场因子和价格水平的历史数据采用SVR进行映射关系的拟合。SVR的核函数采用KBF核函数和线性核函数，逐步缩小超参数优化的范围，可决系数比对结果如表2所示。

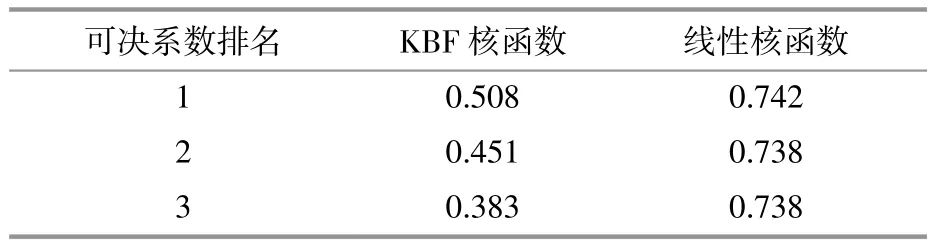
表2 超参数优化结果Table 2 Hyperparameter optimization results

在广东电力现货市场的试运行数据上，线性核函数的表现比KBF核函数优秀，因此采用线性核函数进行电价水平映射关系的拟合。

而后对Vine-Copula进行训练和建模，所得结果如图6所示。

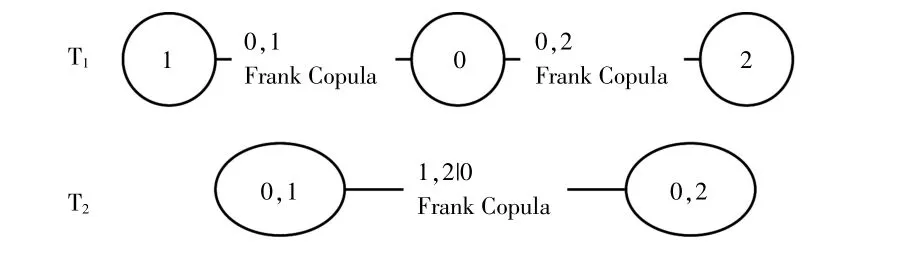
图6 D-Vine建模结果Fig.6 D-Vine modeling results

图 中，T1中 的 节 点0，1，2分 别 表 示 市 场 因子、B类机组竞价空间、量价指数、阻塞度。

3.4 收敛性分析与模型结果

基于上述训练得到的D-Vine Copula和SVR模型，分别采用QMC法和MC法进行市场因子和节点电价水平数据的生成，不同采样次数下样本的方差系数c如图7所示。

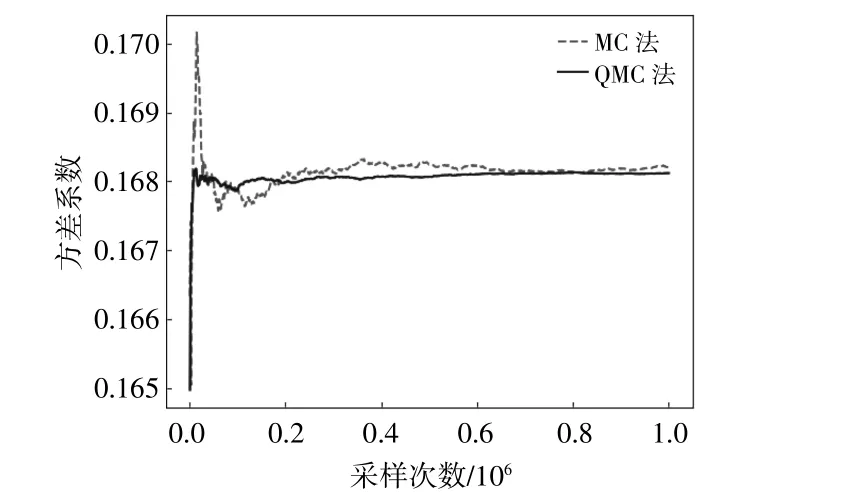
图7 收敛性对比Fig.7 Convergence comparison

由图7可知，QMC法比MC法收敛速度更快，方差系数水平也低。95%置信度下的VaR为130.67元/(MW•h），在 与2020年8月 南 方(以 广东起步）电力现货市场接近的风险环境下，节点A的节点电价在95%的置信度下价格水平将高于130.67元/(MW•h）。结合海上风电和光伏的仿真结果，在95%的置信度下，海上风电和光伏的机组容量利用率分别为0.003 8和0.064 0。以式(11）量化海上风电和光伏参与电力现货市场的风险，在90%的置信度下收益将高于0.50元/MW和8.36元/MW。

4 结论

针对可再生能源未深度参与国内电力现货市场、国内电力现货市场数据量不足的两大问题，本文提出了基于Vine-Copula和拟蒙特卡罗法的可再生能源电力现货市场风险度量模型。模型在每个风险场景下进行风险度量：引入Vine-Copula函数进行多个市场因子依赖关系的表征，解决数据量不足的问题；采用QMC法进行VaR的度量，允许模型适应于逐个风险场景度量风险的高频应用场景。本文基于南方(以广东起步）电力现货市场在2020年8月结算试运行的数据，验证了模型的可行性。