斯里兰卡南部海域次重力波特征研究

2023-12-21沈侃敏郑振钧姜贞强董国海

海洋工程 2023年6期

沈侃敏，郑振钧，王滨，姜贞强，董国海

（1.浙江省深远海风电技术研究重点实验室，浙江杭州 311122；2.中国电建集团华东勘测设计研究院有限公司，浙江杭州 311122；3.大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024；4.中国海洋大学，山东青岛 266100）

海洋中的波浪总是以一定的周期或频率运动。波浪中大部分能量集中在周期为1～30 s 的风浪和涌浪上。风浪由风直接驱动生成，谱峰周期一般在8 s以内。涌浪通常指风浪在离开风区后经过长距离传播形成的波浪，其能量集中在特定的方向和周期附近，周期较大（通常在8 s以上）且传播过程中能量耗散很小，能够影响到非常远的海域。在周期为30～300 s这个范围内的波浪在海洋中也占有很大一部分能量，这类波浪称作次重力波，是由短波群（风流和涌浪）的非线性相互作用生成的。

短波群在非线性作用下会产生约束次重力波（频率为非线性相互作用的两个波浪组分的频率之差，因而也称为差频波，对应周期一般为30～300 s）。约束次重力波随波群传播，相速度等于波群速度，不由色散方程控制［1］。与短波相比，约束次重力波在深海处非常微小，只有几毫米到几厘米。当波浪传播至浅水区域，色散性显著减弱，约束次重力波趋向于满足色散方程，波浪非线性能量传递增强甚至达到“共振”状态［2］，约束次重力波波高会得到显著增长。当短波群在近岸破碎后，约束次重力波会从中释放出来成为自由次重力波，此时波浪传播相速度由色散方程决定［1，3-5］。Symonds 等［6］提出了另一种自由次重力波的产生机理，在波浪开始破碎的过渡区，波浪的破碎点会前后移动，因此在这个区域就会产生一个随时间变化的辐射应力，从而驱动自由次重力波的产生。破碎点移动机制认为短波群破碎后释放出来的自由次重力波很少，而且会在浅水中耗散掉，所以观测到的自由次重力波主要是破碎点移动机制产生的。Schäffer［7］将以上两种机制统一到了一个半解析模型中，认为自由次重力波的产生是这两种机制共同作用的结果。

次重力波在近岸波浪运动过程中起到重要作用，影响到港湾振荡、裂流、泥沙输运、沙丘侵蚀和珊瑚礁水动力等诸多近岸过程［8-11］。因此，次重力波的研究具有重要的科学意义和工程价值。现场观测是研究次重力波的重要方法，可以真实地反映出所有物理过程。但是，该方法往往受到仪器数量的限制，其空间分辨率很差，无法反映出次重力波大范围海域的时空特征。Zheng 等［12］基于海浪谱模型开展了近岸次重力波的大范围海域模拟，但是没有分离出约束次重力波和自由次重力波，因此止步于次重力波总能量的描述，并且没有讨论这两种次重力波与当地短波要素和地形的关系。

介绍了次重力波大范围海域的海浪谱模拟方法。随后，以斯里兰卡南部海域为例，结合现场观测方法和数值模拟方法研究了次重力波的时空特征，阐明了其与当地短波要素和地形的关系，揭示了自由次重力波和约束次重力波的时空特征。文中的研究方法和成果可为次重力波及其对近岸过程影响的相关研究提供参考。

1 波浪现场观测

印度洋具有典型的季风气候，夏季盛行西南季风（6 月至9 月），冬季盛行东北季风（12 月至3 月）。南半球西风带（60°S 至40°S）强风作用下生成的西南向涌浪主导北印度洋全年的涌浪场［13］。特别是在西南季风期间，北印度洋的涌浪高度达到最大值［14］。因此，现场观测在西南季风期进行。

波浪观测仪器按工作原理可分为压力式、声学式、重力式和遥感式等类型［15］。声学多普勒流速剖面仪（acoustic doppler current profler，简称ADCP）是目前应用较为广泛的一种海洋观测设备，基于多普勒原理和矢量合成方法，能够观测波面、波向、海流等信息。挪威Nortek 公司的AWAC（acoustic wave and current）是ADCP 的一款代表产品，采用海底布放方式，避免了海面大风浪或船舶航行对观测系统的影响和破坏，目前在近岸次重力波的观测方面应用广泛［16］，因此选用AWAC进行现场观测。从2019年7月10日持续到9月25日开展观测。由于装置的调整，有些时段（即8 月16 日至17 日）没有数据。每小时进行一次观测，一次34 min，采样频率为2 Hz。

次重力波（0.003 3 Hz ＜f＜ 0.033 3 Hz）波高通过式（1）计算：

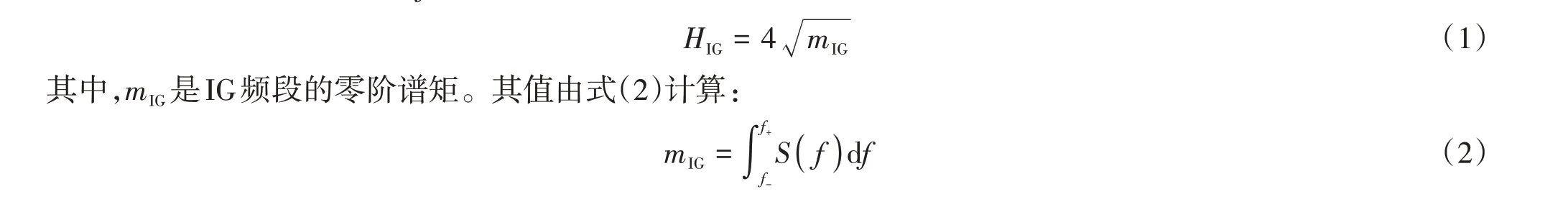
其中，f+和f-是IG频带的上下限，S(f)是波面过程线的谱密度。

2 次重力波的海浪谱模拟理论

大尺度海域的波浪模拟技术已经发展得很成熟，并且被广泛用于近岸区域的波浪预报［17］。大多数波浪模拟技术都是基于第三代的相位平均海浪模型/波浪谱模型开发的，如WAVEWATCH III （简称WW3）［18-19］。然而，一般而言波浪谱模型的三波非线性相互作用局限于各频率组分自我作用产生的倍频项，无法考虑差频项（即约束次重力波）的生成。自由次重力波的传播不依赖于短波的相位。因此，理论上，波浪谱模型可以通过在控制方程中添加自由次重力波源项来模拟其传播和演变。

2.1 WW3自由次重力波源项

在WW3中，球面坐标系下的波作用量平衡方程为：

其中，N=N(k，θ；φ，λ，t)为波浪谱函数，k和θ分别代表波数和波向，φ和λ分别代表经度和纬度，k̇，θ̇g，φ̇和λ̇表示波浪能量在波数、波向和经纬度上的传播速度。方程左侧的第二和第三项描述了波浪能量在平面二维地理空间的传播。第四项代表水深诱导的波数偏移。第五项代表水深诱导的波浪折射。方程右侧代表源项（比如风能输入项）用于描述多种物理过程。

近年来，WW3发展出了许多新特性，比如非结构化网格［20］、近岸植被对波浪的作用［21］、亚网格岛屿阻力源项和自由次重力波模块［22］。WW3在相位平均特性前提下，可以基于简化理论考虑非线性倍频波的产生，但是约束于波群中的差频波（约束次重力波）的生成和传播无法模拟。但是，WW3 理论上可以模拟自由次重力波，因为这部分波浪并不依赖于短波的相位信息。这个数值过程通过以下两个步骤实施：1）只考虑30 s 以内风浪，WW3 计算的频率范围通常是0.03～0.7 Hz，为了覆盖次重力波的频率，WW3 的频率范围应拓展为0.003～0.7 Hz；2）在岸线节点添加自由次重力波源项，之后，自由次重力波可以被约束在大陆架上传播，也可以离岸传播甚至跨越大洋传播。

自由次重力波参数化方案从估计其波高HFIG开始。众多现场观测资料表明，HFIG与当地的短波统计要素（波高、周期）和水深显著相关［23-24］。Ardhuin等［22］基于现场观测资料提出了HFIG的经验公式：

其中，E(f，θ)是WW3 输出的频率方向谱。平均周期Tm0，-2比经验公式中经常采用的谱峰周期更加稳定，并且给予谱的低频部分更多权重［25］。

自由次重力波谱由经验式（6）给出［22］：

其中，g是重力加速度，α1和Δf是经验系数，根据Ardhuin等［22］，一般可取为α1= 0.001 25 s-1和Δf=0.027 9 Hz。cg是频率相关的波群速度，k是波数，k/cg涉及了波浪浅化效应因而该源项可以适应海岸线上不同的水深。根据Ardhuin 等［22］的研究。式（6）决定了自由次重力波谱在f＞ 0.013 Hz 的区域以f-1.0的形式衰减。需要强调的是，式（6）只是自由次重力波谱型的一种经验估计形式，后续研究中可以根据所研究海域的自由次重力波特性制定出更适用的谱形。

进一步假设自由次重力波的能量各向均匀分布，则其方向谱可以表示为［22］：

在WW3 中，自由次重力波源项在岸线反射参数化源项中添加。具体来说，对靠近陆域最近的计算节点，自由次重力波的方向频率谱会取代反射谱中的次重力波频率部分。需要强调的是，岸线反射源项不包含由于非线性相互作用产生的反射次重力波，因而在WW3 计算域中传播的次重力波都是自由次重力波。通过谱积分以及式（1）即可获得自由次重力波波高HFIG。完整的波浪能量谱（包含自由次重力波和约束次重力波）可通过以下两个步骤得到：1）通过二阶非线性理论和WW3的输出谱计算出约束次重力波谱；2）将计算出的约束次重力波谱与WW3 输出谱叠加，即可得到完整的波浪能量谱。二阶非线性约束次重力波谱的计算理论将在下一小节介绍。

2.2 二阶非线性约束长波谱

基于势流理论和以波陡为参数的Stokes摄动展开法，可以求得波浪二阶非线性相互作用产生的约束波，包括差频（约束次重力波）波和和频（高频）波［5，26］，这里只关注差频波。二阶差频耦合系数Db表达式为［26］：

其中，HIG为次重力波总波高。

3 海浪谱模型设置

3.1 大洋模型

大洋模型采用结构化网格建立，计算域如图1所示。图1（a）展示的是外层模型D1，范围为20°E～120°E，60°S～30°N，网格分辨率为0.5°。此外，图1（a）中标记了内层模型D2的范围，并在图1（b）具体展示了D2的信息。内层模型D2 范围为65°E～90°E，0°N～25°N，网格分辨率为0.1°。采用Tolman［27］提出的多重网格法进行两层模型的双向嵌套模拟。使用从0.003 13 Hz到0.071 6 Hz的58个以指数形式增长的频率。D1和D2的方向分辨率分别为15°和10°。

图1 大洋模型计算域示意Fig.1 Computational domain of oceanic models

采用欧洲中尺度天气预报中心（European Centre for Medium-Range Weather Forecasts，简称ECMWF）的再分析风场ERA5（ECMWF Reanalysis v5）驱动风浪生成，空间分辨率为0.25°，时间步长为3 h。从法国海洋开发研究院（IFREMER）全球波浪模拟数据库中提取边界条件施加在外层大洋模型的开边界上。数值时间步长遵循CFL 稳定性准则。按照WW3 的分步法，外部模型D1 中，最大全局时间步长Δtg为1 800 s，对流项的最大CFL 时间步长Δtxy为600 s，谱空间时间步长Δtk为900 s，源项最小时间步长Δts为10 s。在内部模型D2中，上述时间步长分别取600 s、200 s、300 s和10 s。

3.2 近岸模型

图1（b）中标记了近岸模型D3（斯里兰卡南部海域）的范围。图2具体展示了D3的信息。D3计算域包含17 163个三角形单元和8 911个节点。沿岸分辨率约为0.1～0.9 km，近海区域分辨率大概为0.1～2.2 km，这足以分辨海岸线及电子海图中提取的水深数据。频率—方向的离散与上文中大洋模型 D2 保持一致。近岸模型D3 单向嵌套于大洋模型D2 中。在图2 （a）圆圈标记处，从大洋模型D2 提取波浪谱，作为近岸模型D3 外海边界处的边界条件。图2 （b）展示了AWAC 测点的位置（后文简称为G1 测点）。近岸模型D3 同时也受ERA5风场作用（与大洋模型一致）。在进行时间积分时，时间步长分别取Δtg=150 s、Δtxy=50 s、Δtk=75 s和Δts=12.5 s。

图2 近岸波浪模型D3计算域示意Fig.2 Computational grids of the nearshore model

4 斯里兰卡南部海域次重力波特征

4.1 时间序列和谱分析

G1 测点的约束次重力波波高HBIG和自由次重力波波高HFIG的时间序列如图3 所示，为便于分析还展示了短波波高HS和谱峰周期Tp。可以看出，当HS和Tp较大时，HBIG也较大，这实际上与二阶耦合系数的特征有关。以7月11日0时和7月15日22时的数据为例，分别展示短波和根据二阶理论计算的约束次重力波方向—频率谱，见图4和图5。可见短波谱密度较大的区域由南向波浪主导，各波向分量的夹角都在30°以内，并且周期均大于10 s（也即频率均小于0.1 Hz）。7月15日22时短波谱的谱峰频率更低，且谱密度更大。此外，周期越大、夹角越小则二阶耦合作用越强，因此7 月15 日22 时产生的约束次重力波远强于7 月11 日0 时。目前基于短波要素估计次重力波波高的经验公式只考虑了短波波高、周期和水深，没有考虑短波的方向分布集中特性，这可能是经验公式误差的重要诱因。因此，短波的方向分布参数应纳入将来次重力波波高的经验公式中。

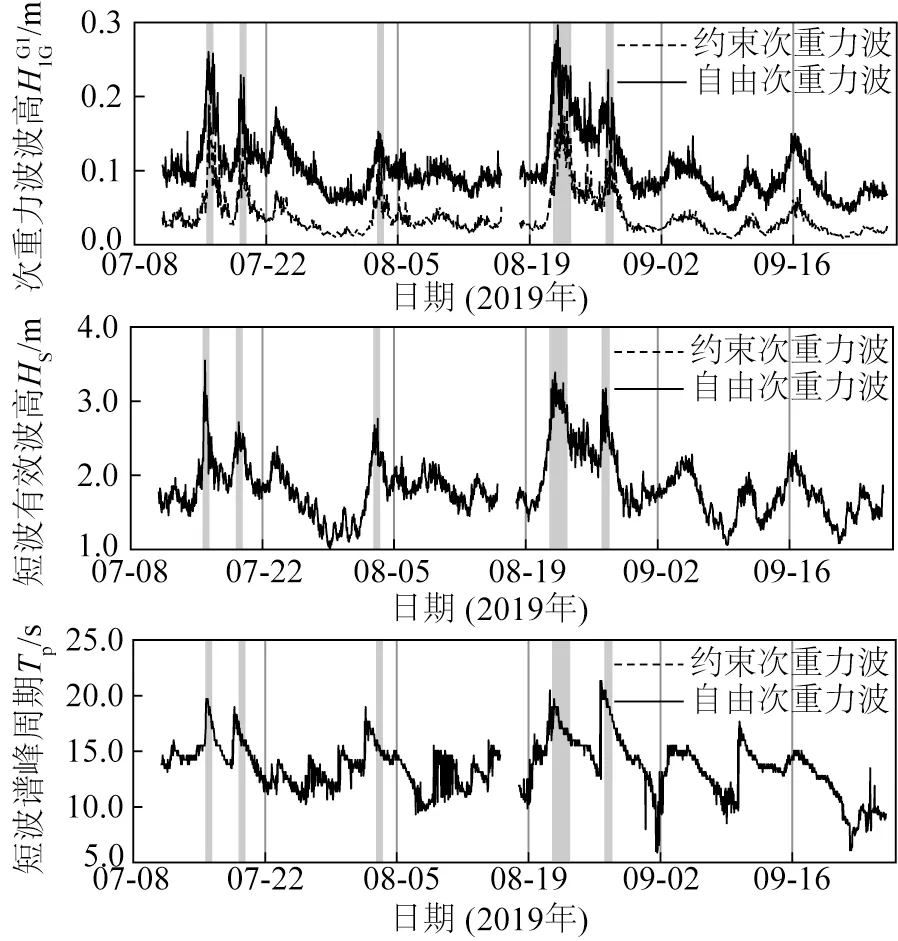
图3 G1测点波要素的时间序列Fig.3 Time series of bulk wave parameters at G1 sensor

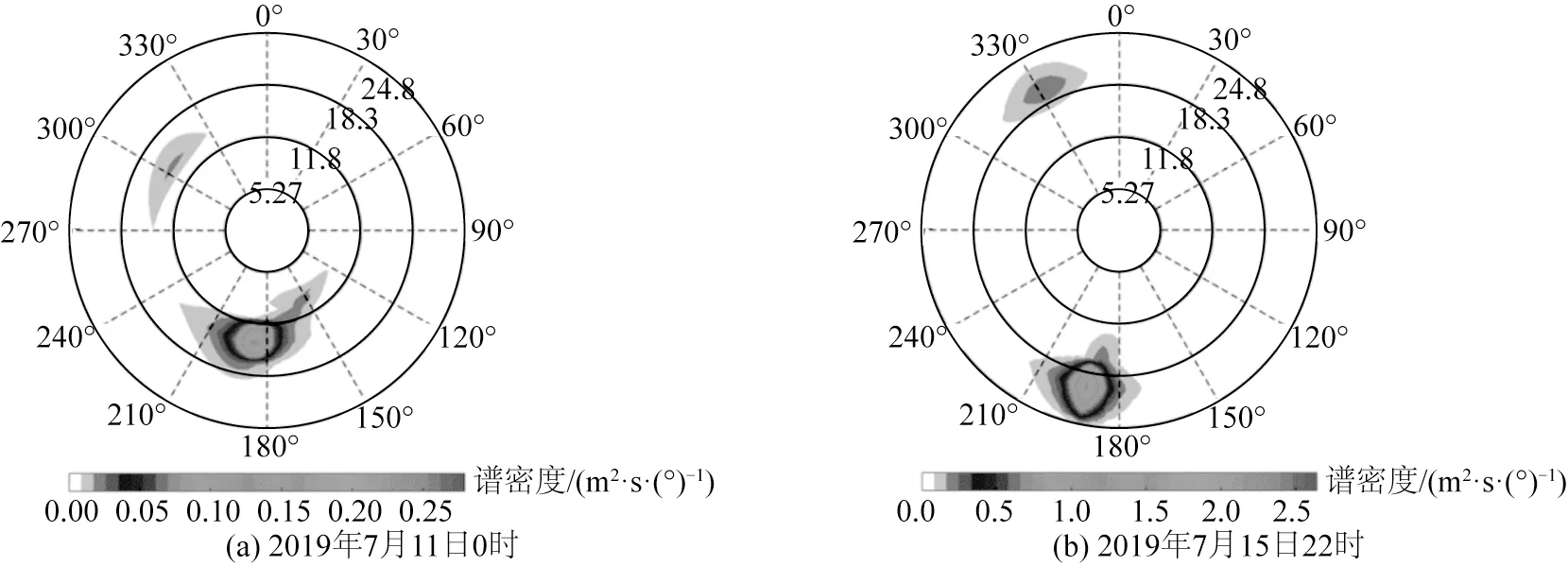
图4 实测的短波方向—频率谱Fig.4 Measured frequency-direction spectra

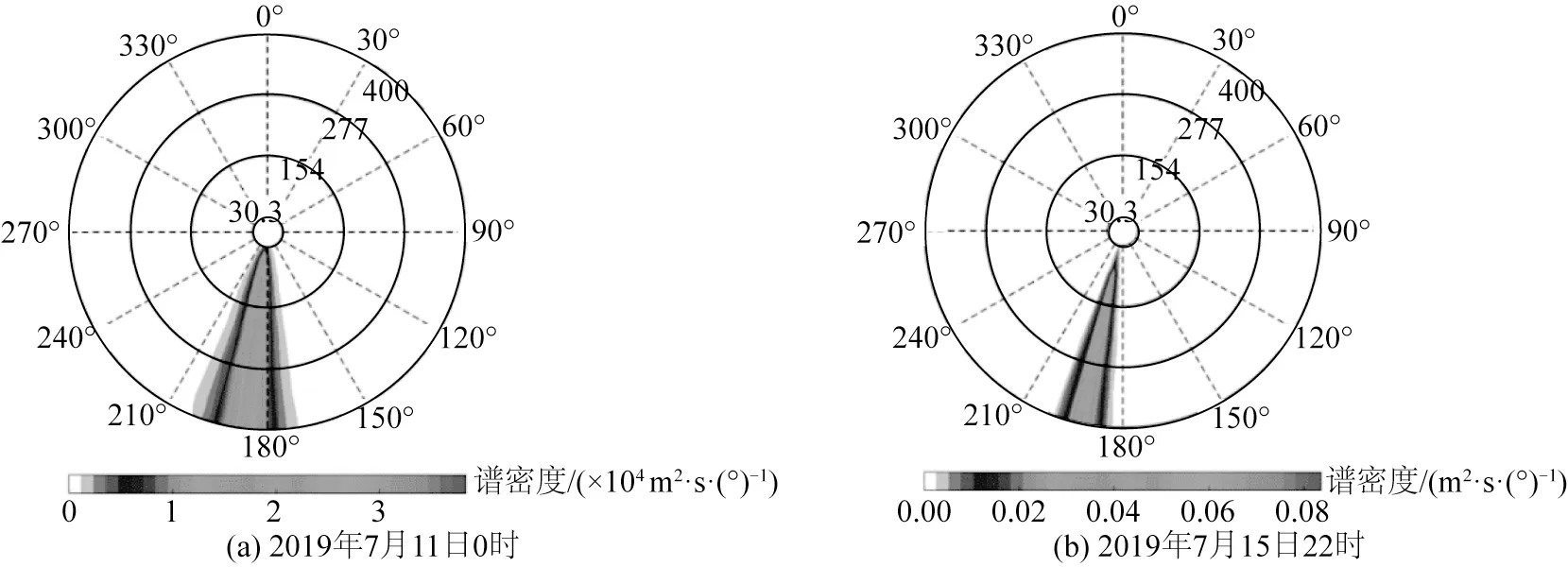
图5 基于二阶理论计算的约束长波方向—频率谱Fig.5 Direction-frequency spectrum of bound long wave based on second order theory

Bowers［23］基于大量现场观测数据，分析了不同海域HBIG和HFIG的特征，结果表明在低强度海况下，HFIG往往数倍于HBIG，但随着总波高的增大，次重力波中约束成分的占比逐渐提升，甚至要略高于自由成分。在图3中也可以发现一致的规律，在大多数时间HFIG大于HBIG，但在强涌浪海况下（见图3灰色区域标记的时期），短波波高和周期均非常显著（短波波高大于2.5 m，周期大于15 s），HBIG逐渐逼近甚至超过HFIG。

据文献数据显示，英国南部海域塔尔伯特港外的HIG为0.025～0.407 m，HIG/HS为0.041～0.117，测点水深为10 m［23］。美国北卡罗莱纳州海域的HIG为0.038～0.49 m，HIG/HS为0.060～0.184，测点水深为8 m［28］。文中研究区域G1测点的HIG范围为0.044～0.31 m，HIG/HS为0.029～0.119，测点水深为18 m。可见，G1测点的HIG以及HIG/HS与文献中典型的次重力波强劲海域的HIG以及HIG/HS是处于一个量级的。需要强调的是，G1测点的水深相比之下要深的多。对于斯里兰卡南部海域水深更浅的区域，非线性作用更强并且更靠近自由次重力波源项释放岸线，因而HIG以及HIG/HS的上限会更大。

HBIG和HFIG与短波波高相关系数分别为0.91 和0.84，后者与短波的相关性相比之下稍弱一些。G1 测点记录到的自由次重力波可能包含4种成分：1）短波在水深更深处释放并向岸传播的自由波；2）短波在岸线破碎产生的离岸传播的自由波；3）沿岸传播的边缘波；4）其他遥远岸线产生并越洋传播而来的自由次重力波。目前无法定量分离出这4种成分，但可以给出定性的推测：第1种和第2种成分与G1测点短波浪场相关性可能是最强的；而边缘波不一定是在G1 测点海域产生的，可能是斯里兰卡南部海域其他岸线，因此边缘波与G1 测点当地短波浪场相关性可能差一些；越洋自由长波与当地短波浪场的相关性是最差的。因此，自由长波和当地短波也有显著的相关性（0.84），但是要稍弱于约束长波与短波的相关性（0.91）。

4.2 次重力波空间特征

WW3数值模拟结果和现场观测结果对比见图6。考虑到波浪周期在次重力波源项中也是重要的参数，因此同时采用有效波高HS和代表性平均周期来解释次重力波结果。次重力波源项中采用了Tm0，-2=代表平均周期，这里的讨论采用类似的但是应用更广泛的量Tm02=m0/m2代表平均周期，其中m0和m2代表谱的零阶矩和二阶矩。可以看出数值模拟结果和现场观测结果整体吻合得很好，WW3 可以较准确给出短波和次重力波的统计结果。

图6 现场观测数据与数值模拟结果的对比Fig.6 Comparison of the in-situ observed values and numerical results

不管是HBIG还是HFIG，其大小实际上都由短波参数决定。对于HBIG，周期越大，二阶作用越强。同时，短波波高越大，二阶作用生成的约束长波越强。对于HFIG，源项强度直接由短波波高和周期决定。因此，从图6 （c）、（d）、（e）可以看出，次重力波波高（HIG、HBIG和HFIG）被低估与短波参数（HS和Tm02）被低估有着很强的相关性，也即两种低估经常在同一日期出现（如图6标注的Period 1和Period 2）。反之亦然，也即在某些时期次重力波波高被数值模拟高估也与短波参数（HS和Tm02）被高估有关系，如图6标注的Period 3和Period 4，此处对HS和Tm02轻微地高估导致了HIG显著大于现场观测值。总体而言，WW3 模拟出的HBIG和HFIG与现场观测值吻合良好。可以进一步采用WW3给出次重力波的空间特征。

图7 展示了HS和HFIG在WW3 模型D3 的空间分布，波高由2019 年7 月11 日至9 月25 日的结果平均而来。外海边界的HS大约为2 m，波浪向岸传播过程中，由于海底摩擦和波浪破碎的作用，HS持续降低直到在岸线节点达到约0.8 m。外海边界的HFIG约为0.02 m（边界水深约为3 000 m），向岸过程中，HFIG快速增长，直到在岸线节点达到约0.2 m（水深约为2 m）。HFIG的离岸衰减由以下两个因素造成：1）自由次重力长波源项布置于岸线，当其离岸传播时，由于波能流守恒，波高会越来越小；2）离岸过程水深越来越大，反浅化作用会使得波高降低（也即能量一定时，波长越长，波高越小）。

图7 波高分布Fig.7 The distribution of wave heights

因为每次由短波谱计算HBIG需要经过4 层循环，若要给出HBIG的空间分布则需要极大的计算量。因此，只选择G1 测点位置到边界位置的一条线段（即图7 所示黑色虚线）定量展示HS、HBIG和HFIG特征，见图8。图8 （a）给出了斯里兰卡水深分布剖面图，可以看出目前剖面的大陆架宽度只有20多千米，而斯里兰卡大陆架宽度一般在5～25 km，可见斯里兰卡大陆架极其狭窄。从图8 （b）可以观察到，波浪进入大陆架后，水深逐渐小于波长，地形对波浪传播产生明显影响，HS降低的趋势增强。随着水深的减小，二阶耦合系数增大，因而约束长波逐渐增大。理论上，HBIG正比于h-5/2。图8 （c）绘制了HBIG和h-5/2曲线，可见两者趋势吻合很好，HBIG在水深小于50 m 后才开始显著增长。自由次重力波是在岸线产生的，向外传播过程中会经历反浅化过程，波高变化遵循h-1/4规则。HFIG和h-1/4曲线绘制于图8 （d）中，可以发现两者趋势吻合良好。总体而言，HBIG对水深更加敏感，在水深极浅区域，HBIG有可能大于HFIG。而随着水深的增大乃至达到深海，HBIG迅速减小，此时是自由次重力波主导长波场。

图8 G1测点位置剖面水深和波高的离岸分布Fig.8 Offshore distribution of topography and wave height of the profile at the measuring point G1

中国大陆架非常宽广（数百公里宽的大陆架十分普遍）且有岛链掩护，涌浪在大陆架上经过长距离的传播将有明显的能量损耗，使得沿海大部分地区的涌浪环境并不显著，因此，规范以风浪为主，很少考虑次重力波及其引发的近岸水动力灾害如港湾振荡。相比之下，斯里兰卡大陆架极其狭窄，对涌浪的能量损耗作用极为有限，使得近岸面对着强劲的涌浪及其伴生的次重力波的侵袭，增大了次重力波引发的近岸水动力灾害的风险。