规不正，不可为圆

郝占峰

“规不正，不可为圆”阐明了遵守规则的重要性，也从侧面反映了规范化解题的积极意义.规范化解题不仅能提升初中生数学解题效率，还能通过规范化审题、解题步骤书写以及解题答案求算等，发展学生的逻辑思维能力，辅助学生建构科学完整的数学解题模型，进一步强化学生知识综合运用能力，以满足素质教育对学生逻辑思维、推理分析等学科思维能力的发展要求.

1 初中数学解题规范化教学的积极意义

1.1 有助于提升学生解题效率

解题规范化教学活动的开展，有助于提升初中生数学解题效率.这主要是因为解题规范化教学活动的开展，使得学生审题、解题更为规范细致，精准掌握数学问题题干所给予的条件以及解题目的，进而掌握解决问题的思路方法，并做到科学严谨地处理数学问题，规范化书写解题步骤，精准求出最终答案.这样学生就能有效避免由于解题不规范而造成的解题错误、失分现象，实现数学解题效率的显著提升.

1.2 有助于翻转师生课堂角色

解题规范化教学活动的开展，有助于巩固强化学生课堂学习的主体地位.相较于传统的应试式解题教学活动，解题规范化教学活动与学生个体联系更为紧密，大多数情况下都是基于不同学生个体的实际情况，针对性开展解题规范化教学活动，旨在个性化提升学生的规范化解题能力，确保所有层次学生都能按照自身的解题习惯，科学提升个人数学解题的规范性，而不是一刀切地完成所布置的解题规范化学习任务.这样无形中便提升了学生在解题规范化教学活动中的主体地位.由此可见，数学解题规范化教学活动的开展，有利于推进数学课堂师生角色地位的翻转.

1.3 有助于转变教师教学思想

解题规范化教学活动的全面落实，能逐步转变教师的解题教学思想.教师作为解题规范化教学活动的引导者，要想更好地推进规范化解题活动，应降低应试教育等传统教育思想观念对个人解题规范化教学指导工作产生的消极影响.教师往往会积极学习素质教育、解题教学规范化等育人理念，掌握规范化解题教学的核心，逐步转变个人的解题教学思想，以实现教育思想转变导向数学解题规范化教育手段改革，最终达到充分发挥教师规范化解题教学指导效能目的.因此，规范化解题活动的开展，有利于逐步转变教师的解题教学思想.

2 初中数学解题规范化教学的具体策略

2.1 传授规范审题方法，辅助学生正确理解题干

审题作为解题的第一个环节，其规范与否直接影响着学生对题目题干条件的理解程度，决定着后面每一个环节解题活动能否顺利开展，故此环节的解题教学规范化影响极为深远.同时，审题规范化技巧的传授，能帮助学生精准高效掌握数学问题的题干核心，弄清数学问题各个条件之间的逻辑关系，为后续问题的深度思考分析提供方向，是学生解题规范化学习参与不可或缺的一环.为此，教师可先在解题规范化教学活动中，传授给学生一些审题的方法技巧，诸如题干重点词下划线、隐含条件的着重分析以及多情境的题干解读等，使得学生掌握更多规范有效的问题题干解读技巧，用于辅助个人后续规范化审题，进而实现科学规范分析数学问题题干要素内涵的目的.

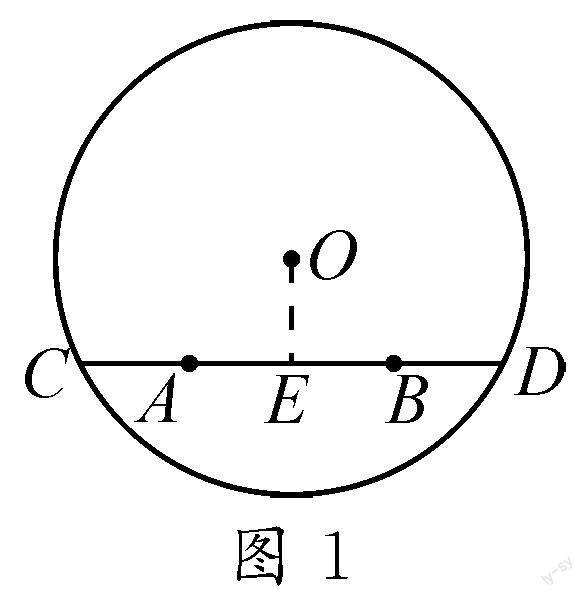
以“圆”的解题教学为例，呈现题目：已知线段AB在圆内，直线AB与圆O相交于C，D两点，并且BD=AC，如图1所示，那么OB=OA吗？

为辅助学生更好地掌握本问题所考查的知识点以及题干核心，教师可着重引导学生运用规范审题技巧，先在条件“BD=AC”以及问题“OB=OA”两个重要题干要素下画上横线.然后让学生尝试过圆心O作AB垂直OE于点E，进而可得DE=CE.而学生后续只需要结合上面规范化审题所圈画的核心题干要素，便可发现因为“BD=AC”，所以可得BE=AE，证明OE为AB的中垂线，并根据圆的垂径定理证明OB=OA.这样，通过规范审题技巧的传授，帮助学生精准掌握与“圆”有关问题题干的重点要素，辅助学生找到解决问题的方向，最终达到提升学生数学审题规范程度的目的.

2.2 规范解题步骤书写，提升学生解题规范程度

科学规范的解题过程，不仅是学生思考数学问题流程的重现，也是学生数学答题素养的重要体现.但是，部分学生为了追求解题效率，大多会跳步或缩写解题的流程，以更为简便的形式书写解题流程.如果在重要步骤或关键步骤处突然出现跳步或缩写，那么批阅者可能弄不清解题的思路方向，因而造成解题失数.对此，初中数学教师解题规范化教学活动开展的第二步，便是要规范学生解题步骤的书写，在精简解题步骤的同时要避免重要步骤的省略，并做到科学使用规范的数学语言，逻辑严密地通过解题步骤展现解题思路，以此来提升教师对学生解题步骤规范性及科学性的认可程度，避免出现不必要的扣分现象.

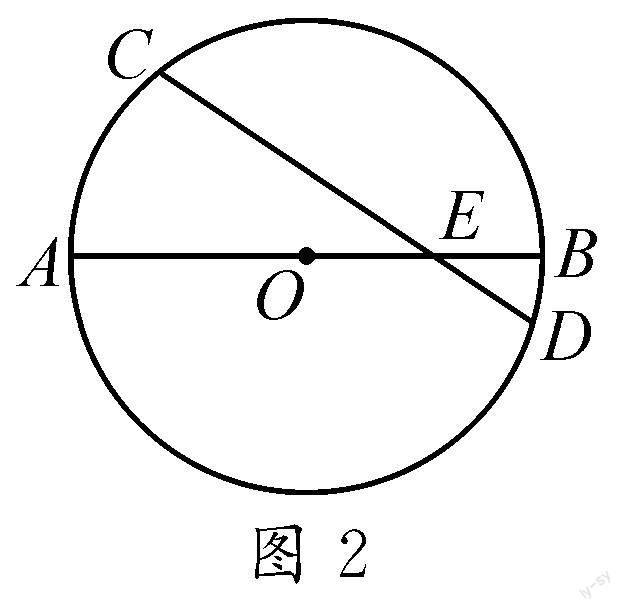
再如：在圆O中，已知弦CD和直径AB相交于点E，∠CEA＝30°，如图2所示，若EB=2 cm，AE=6 cm，请求出CD的长度.

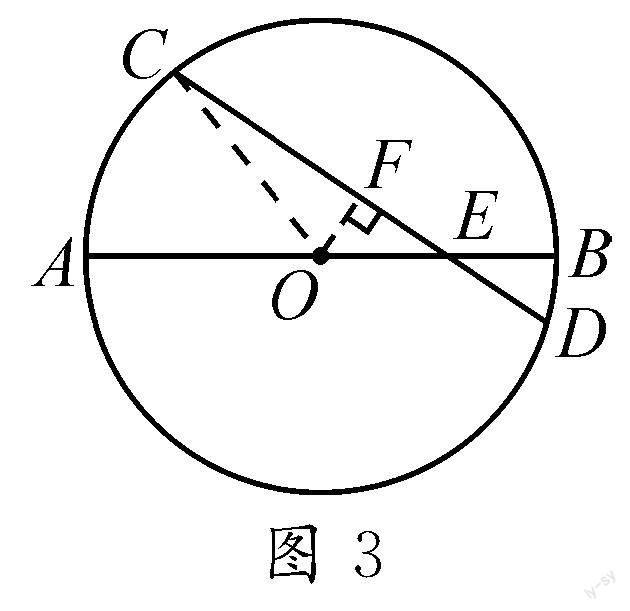
在本问题中，学生可通过构造一个以半弦、半径以及弦心距为三边的直角三角形，如图3

所示，以求出本问题中的未知量.部分学生在完成过圆心O作CD垂直OF于点F，并连接CO后，会忽略“∵EB=2，AE=6”而直接得到“AB=8”，但这样的解题步骤书写并不规范.所以，教师应当严格要求学生按照如下步骤进行书写：

过圆心O作CD垂直OF于点F，并连接CO.

∵EB=2，AE=6，

∴AB=8.

∴OA=4.

∵在Rt△OEF中，∠AEC=30°，

∵Rt△COF中，OF=1，OC=4，

∵CD⊥OF，

∴DF=CF.

这样教师通过规范化解题步骤的演示，帮助学生了解到因果关系解题叙述不明确会失分，日常解题步骤书写应当避免跳步情况的出现，尽可能按照解题思路进行规范化书写，并精简解题步骤，避免赘述情况的发生，最终达到显著提升个人解题步骤书写规范性的目的.

2.3 规范书写解题结果，强化解题答案求算规范

解题答案的书写作为解题规范化教学的最后一环，也是学生日常解题应当关注的重要对象.因为部分学生在完成规范化审题及解题步骤书写后，容易出现懈怠心理，至使所求得的答案并非最简，或者所得到的答案并不符合题干的要求，而这些都是数学解题答案不规范的重要表现.对此，为更好地建构一个科学完整的规范化解题流程，避免学生解题答案出现不规范的现象，教师应积极推进解题答案规范化工作的开展，结合题干的要求，进一步优化所得到的答案.同时，还应要求學生进行答案的二次检验处理，将答案代入到具体数学问题中进行演算求证，以保证所求得的答案真正符合题意.

以“圆”的解题规范化教学为例，教师可引入问题“以等腰三角形的一个腰为直径的圆与底边的交点平分底边”，经过前面规范化审题、规范化解题步骤书写的训练，学生通过设AB，AC为等腰三角形的腰，并且AB为圆O的直径，底边BC与圆O交于点D，证明得到D为线段BC的中点，且AD为△ABC的高，AD垂直于BC，再根据等腰三角形三线合一的性质证明问题.而教师则需在学生完成问题的规范化步骤书写后，要求学生尝试利用“等腰三角形的三线合一性质”进行问题答案的二次求证，检验各个环节的证明步骤是否规范，以保障证明过程的科学性与规范性.这样，教师也借此强化了学生的解题答案规范化思想意识，促使学生关注与重视日常数学解题答案的规范程度，确保所求得的数学问题答案最优、科学合规且符合题目要求，实现数学解题规范化教学的有效闭环，巩固规范审题、规范解题步骤书写的学习成果.

初中数学教师需要针对学生的解题能力发展诉求，通过规范审题、解题过程步骤规范以及解题结果规范等多环节规范化解题教学活动的开展，建构完整的数学规范化解题教学模型，引导学生养成规范化解题的良好习惯，显著减少因解题不规范而造成的失分、丢分现象，最终达到提升解题效率的目的.