基于高空间分辨率BOTDA的土体沉降监测研究

李林海,郭文娟,丁 强,王光辉,高金良,关 鹏,隋景林,张洪英*,刁美玲

(1.哈尔滨理工大学 测控技术与通信工程学院,哈尔滨 150080;2.北京首创生态环保集团股份有限公司,北京100052;3.哈尔滨工业大学 环境学院,哈尔滨 150090;4.鞍山睿科光电技术有限公司,辽宁 鞍山 114000;5.哈尔滨功达给排水技术有限公司,哈尔滨 150028)

地面沉降因其不易被察觉的特性而经常被忽视,从而会导致多种自然灾害,对人类的生命安全造成严重威胁.目前对于地面沉降的监测和安全评估已经成为亟待解决的重要课题.土体沉降的空间分布形态受多种环境因素的影响,刘成禹等人[1]为了能够将地下管道形变对土体沉降的影响可视化,进行了管道破裂诱发沉降的模型预测.

分布式光纤传感技术利用光纤中的散射效应作为传感机制,具有实时性好、灵敏度高、易于组网、受环境影响小、抗电磁干扰等诸多优点[2-3].随着该技术对温度和应变的监测能力进一步提升,已被应用到了土堤沉降[4-5]、管道[6-7]、桥梁[8]、隧道变形[9]等多个领域.分布式光纤传感技术应用于土体沉降监测的关键在于保证光纤本身与被测对象的变形一致性[10-11],Michael Iten等人[12]通过布设光纤来监测岩土体或结构体的变形稳定性,向伏林等人[13]为了研究光纤与土体的变形一致性对二者的协调性进行了离散元数值模拟.对于耦合变形问题,国内外的专家学者均做了有益探索.例如Zhang等人[14]通过光纤在土中的拉拔实验,分析了光纤-土体界面的力学特性,进而提出了两者变形耦合的3个阶段.瑞士学者Hauswirth等人[15]对光纤在大尺度剪切工况下的响应模式进行研究,相关结论对工程应用有一定启发.

在工程实践中,位移量可作为通用的土体稳定性评价指标,因此建立光纤沉降位移与应变之间的关系模型,即可利用分布式光纤传感技术通过测量应变分布实现对土体沉降位移的监测.

分布式布里渊光纤传感技术具有测量范围广、精度高[16]、空间分辨率高[17]等诸多优点,本文利用可实现高空间分辨率的差分脉冲对布里渊光时域分析(Differential Pulse-width Pair Brillouin Optical Time Domain Analysis, DPP-BOTDA)技术对土体沉降进行监测研究.通过搭建土体沉降模拟装置,借助装置内的活塞运动改变土体沉降位移,对监测段光纤的应变分布进行了测量,并通过建立沉降位移与应变之间的关系模型实现了对土体沉降位移的测量.在此基础上,研究了光纤的应变测值与土体纵向位移的关系,对比分析了沉降测量结果与实际沉降之间的关系以及光纤与土体的耦合性能对监测效果的影响,研究结果对利用分布式光纤传感技术进行土体沉降监测具有参考意义.

1 测量技术及原理

1.1 高空间分辨率BOTDA技术

BOTDA技术是基于布里渊散射的分布式光纤传感技术,光纤既是传输介质又是传感元件,利用光波在光纤中的传输特性,可沿光纤长度方向进行连续测量[18].布里渊散射同时受到应变和温度的影响,当光纤沿线的温度发生变化或者存在轴向应变时,光纤中的背向布里渊散射光的频率(称为布里渊频移)将发生漂移,布里渊频移的变化量与光纤应变和温度变化呈线性关系,表达式为:

ΔυB=ΔbT+Δbs=CT·ΔT+CS·Δε

(1)

其中:ΔυB是布里渊频移的变化量;CT和CS分别为光纤布里渊频移的温度系数和应变系数;ΔT和Δε分别是温度和应变的改变量.

如果测量在较短时间内完成,温度变化可忽略不计,则可以通过测量光纤的布里渊频移得到应变情况:

Δε=ΔυB/CS

(2)

在BOTDA系统中,泵浦光的脉宽直接影响信噪比和测量精度,泵浦光的脉宽越窄,空间分辨率越高,但信号强度越弱;泵浦光的脉宽越宽,信号强度越强,但空间分辨率越低.而且当泵浦光脉宽小于10 ns时,会使布里渊增益谱展宽,减弱布里渊散射信号,降低信噪比[17].因此传统BOTDA 技术的空间分辨率最高为1 m,而对于精度要求较高的监测应用而言远远不能满足要求.DPP-BOTDA是利用不同宽度的一对脉冲泵浦光获得两个时域的布里渊增益信号,通过一个小的脉宽差获得远超传统 BOTDA 技术的空间分辨率.本文使用的分布式布里渊温度应变解调仪空间分辨率为5 cm.

1.2 沉降位移测量原理

待测光纤在被测土体中水平布设,当某处土体发生沉降位移时,光纤随之产生形变,如图1所示.图1中L为实验段光纤原长度,A点为光纤的固定夹点,L1为实验段光纤向下位移Y1伸长后的长度,L2为实验段光纤向下位移Y2伸长后的长度.

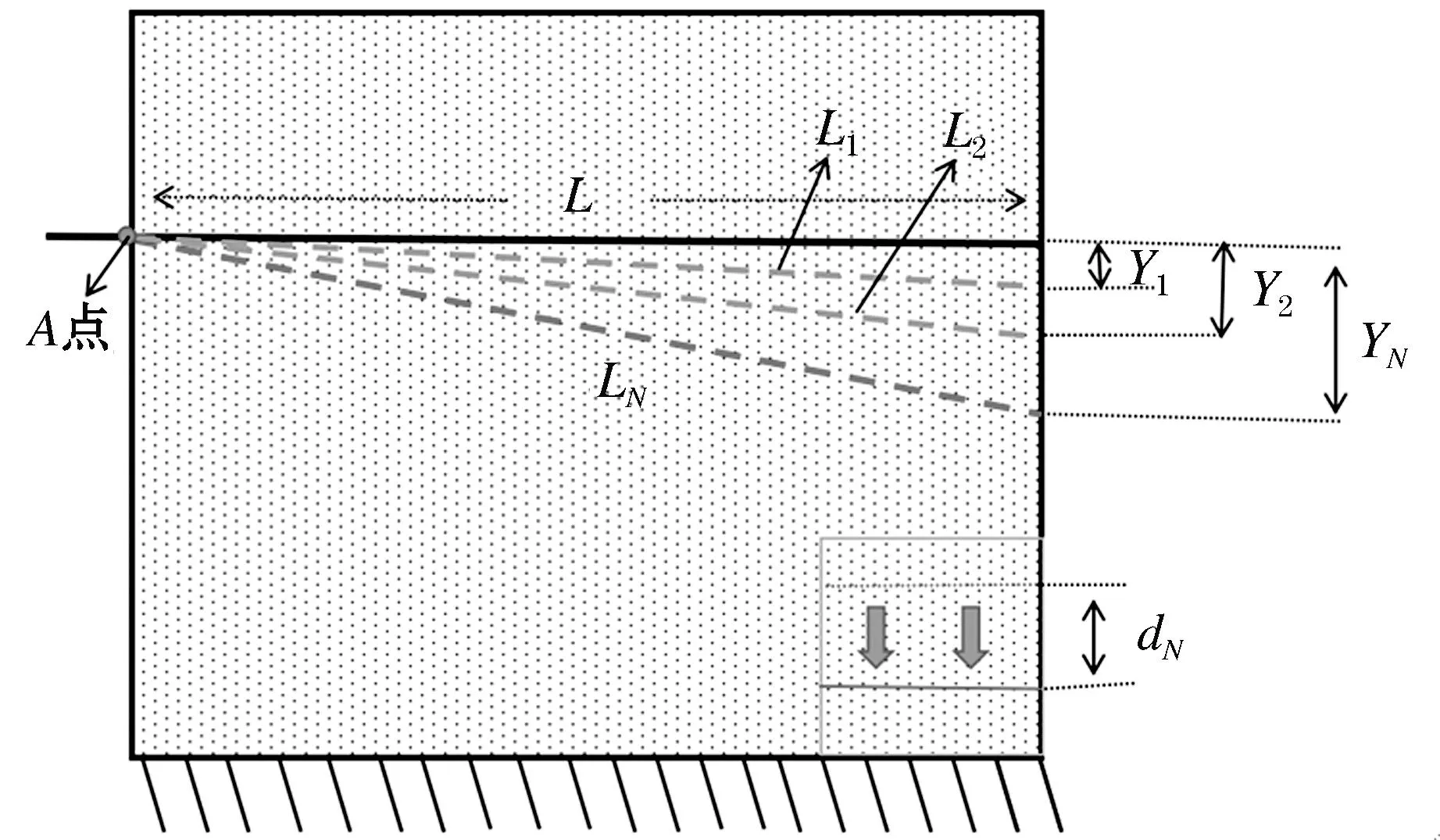
图1 土体纵向沉降剪切面示意图

该段光纤经过沉降分别伸长到L1和L2时发生的应变量ε1和ε2可分别表示为:

ε1=(L1-L)/L

(3)

ε2=(L2-L)/L

(4)

根据图1所示的几何关系以及式(3)、(4)可得对应的沉降位移Y1和Y2,以及当光纤随土体沉降后,由此时测量到的光纤应变值εN可计算出竖向沉降位移YN为:

(5)

(6)

(7)

2 土体沉降实验设计

2.1 实验装置

实验采用的土体沉降模拟装置如图2所示,其中图2(A)为实验装置实物图,图2(B)为实验装置尺寸示意图.本模拟实验箱长220 cm、宽50 cm、高60 cm,填土高度为60 cm,光纤的水平埋设位置距实验箱底部30 cm,两端接入分布式布里渊温度应变解调仪.模拟箱下方安装有升降台,通过改变升降台的高度可以使得实验箱中的土体发生不同的纵向位移,应变传感光纤也会随之受拉变形发生相应的纵向位移.

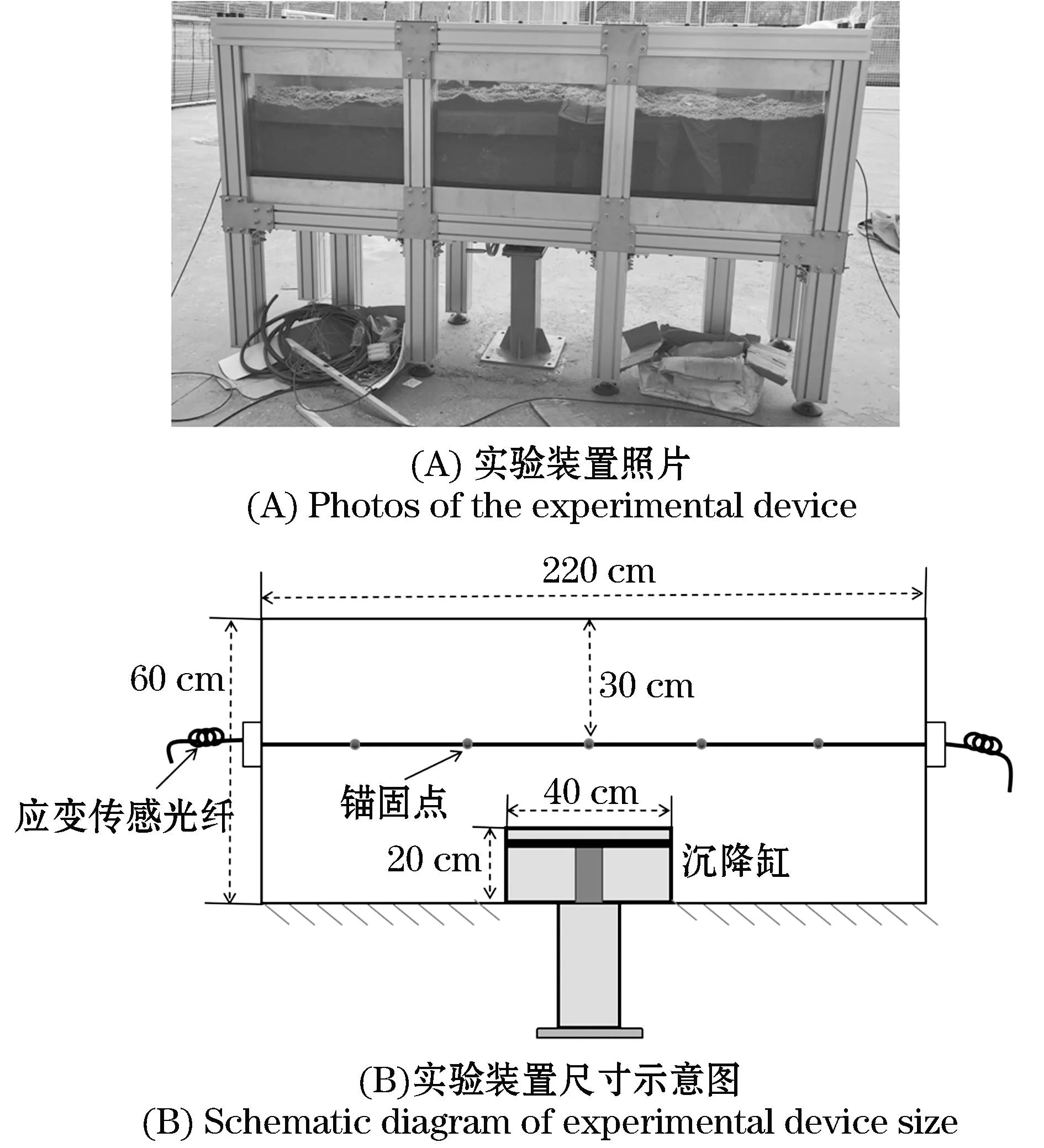
图2 实验装置

沉降实验用土取自鞍山市立山区的砂土,晒干后做实验用.根据土的工程分类标准(GB/T 50145-2007),实验用砂为粗砂,其干密度为1.65 g·cm-3、天然含水率约为5%.实验采用的应变传感光缆型号为RP-S-05-MR,布里渊频移应变系数为0.0482 MHz/με.

2.2 实验方案

在模拟土体沉降实验中,以土体没有沉降时的初始应变测值为基准,在其他实验条件相同的情况下,分为3种不同的工况进行实验,参数如表1所示.其中工况1是在实验箱内无土,将传感光纤用地锚固定在升降台上进行的,用于模拟理想的土体沉降状态.工况2与工况3均为实验箱内有土状态,区别在于有无光纤锚固点,用于对比光纤布设方式对沉降测量结果的影响.

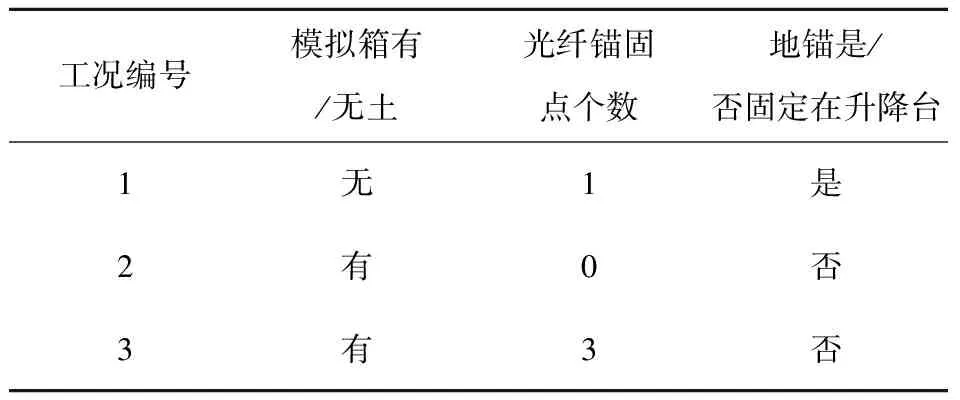
表1 实验的三种工况

3 实验结果分析

3.1 应变-位移数据分析

图3是不同沉降位移下工况1实验段光纤的应变分布图.由图3可知,在实验箱内无土的状态下,光纤沿线的应变分布较为均匀,但是在实验箱两端对光纤进行固定时会给光纤施加夹力,使得光纤两端的应变测值较大.随着升降台每带动实验段光纤向下移动1.3cm,光纤的应变测值递增,当位移为8.3cm时,最大应变测值约为2 700 με.

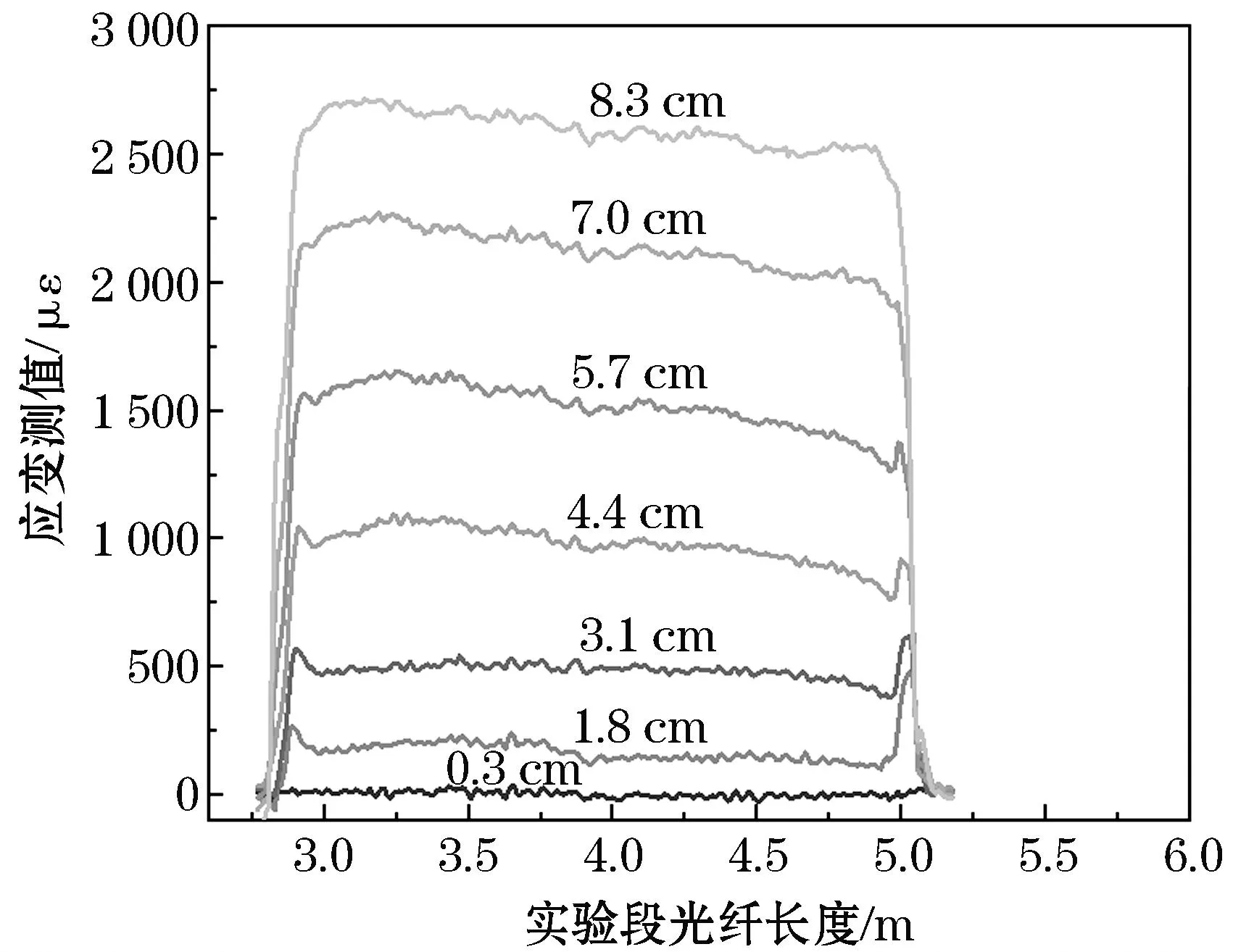
图3 不同沉降位移下工况1实验段光纤应变分布

图4、5分别是不同沉降位移下工况2和工况3实验段光纤的应变分布.由图4、5可知:光纤埋设在土体中因为布设方式的不同和固定光纤时夹力的不确定性,会使光纤的应变测值呈现出不同的分布形状和峰值.如图4所示,在土体带动光纤沉降的初始阶段,工况2光纤周围的围压增大,光纤随着土体的沉降而下降,应变测值整体上随之增大,最大应变值约为1 900 με.只是当光纤沉降达到2.44 cm时,光纤的应变测值约为750 με,土体继续带动光纤沉降到达3.05 cm,此时光纤的应变测值并未发生变化.紧接着土体继续沉降到3.66 cm,此时的应变测值又开始增大,达到约850 με.分析是由于工况2光纤没有任何固定措施直埋于土体中,发生沉降时会发生相对横向滑移,由于土体的不均匀沉降,使得下沉的砂土会移动到光纤下部将其托起,从而导致光纤在沉降到某个位置时应变值不再发生变化.当土体继续沉降时,被托起的光纤会发生弹性形变,从而使应变测值继续增大.工况3条件下光纤上布设有地锚,可以避免光纤发生相对横向滑移,增大光纤与土体的接触面积,减少光纤上方砂土的向下移动,所以光纤的应变随土体沉降位移的增加有规律地增大,如图5所示,当沉降量为7.32 cm时,测得光纤的应变最大值约为3 200 με.

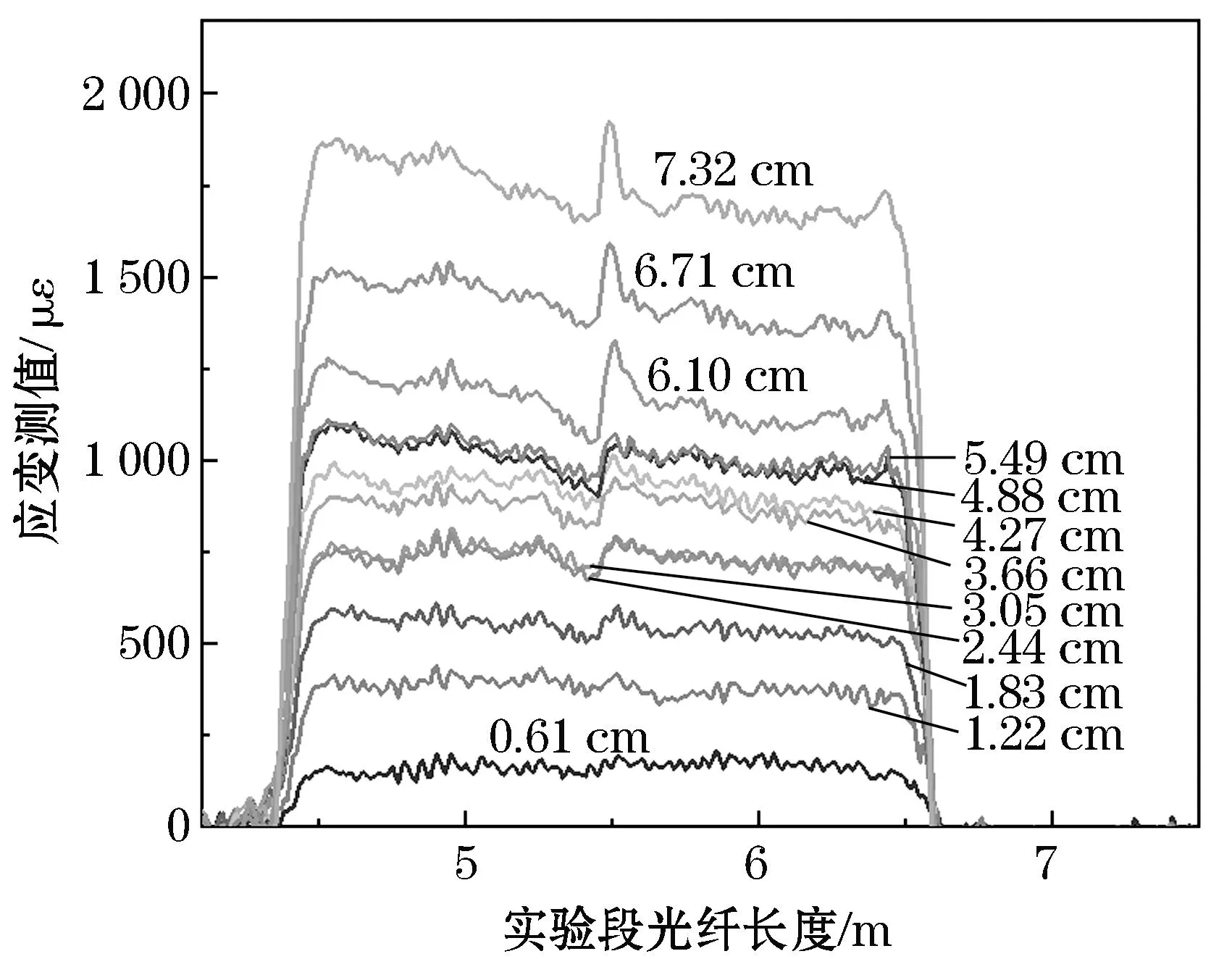
图4 不同沉降位移下工况2实验段光纤应变分布

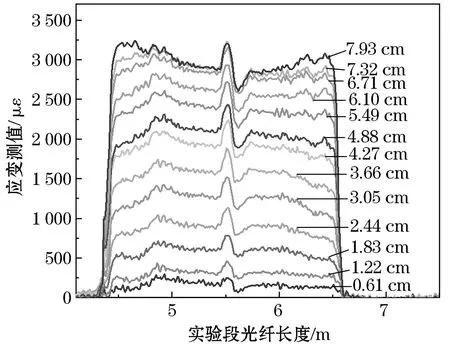
图5 不同沉降位移下工况3实验段光纤应变分布

将图3～5中传感光纤中心位置的应变测值分别代入式 (7)计算得到各工况条件下光纤的沉降位移曲线,与土体实际沉降位移对比如图6所示,图6中横坐标表示升降台位移量,纵坐标表示沉降位移测量值(其中工况2及工况3由于覆土造成沉降时会有固定偏差,故在计算位移时以第一次沉降时的位移作为基准进行位移矫正,默认第一次位移为准确值).由图6可知:工况1条件下光纤的沉降位移测量值与土体的实际沉降位移吻合很好,这说明运用BOTDA系统监测土体沉降具有可行性.工况2和工况3在土体沉降初始阶段沉降测量值都与实际沉降位移符合较好.工况2中当土体沉降达到3.05 cm时,位移测量值与实际位移值发生明显偏离;而工况3实验段光纤因为布设有地锚,接触面积的增大使光纤整体受力增大,当土体沉降到5.49 cm左右时,由于光纤受土体的围压过大,实验箱两端夹具固定不住光纤使其从实验箱两端开始发生滑脱,此时光纤的位移计算值开始偏离实际位移值.由此可以推出光纤在土体中的沉降位移与光纤和土壤间的耦合性存在某种关系,且这种关系可能受土体的不均匀沉降和光纤弹性形变等影响.

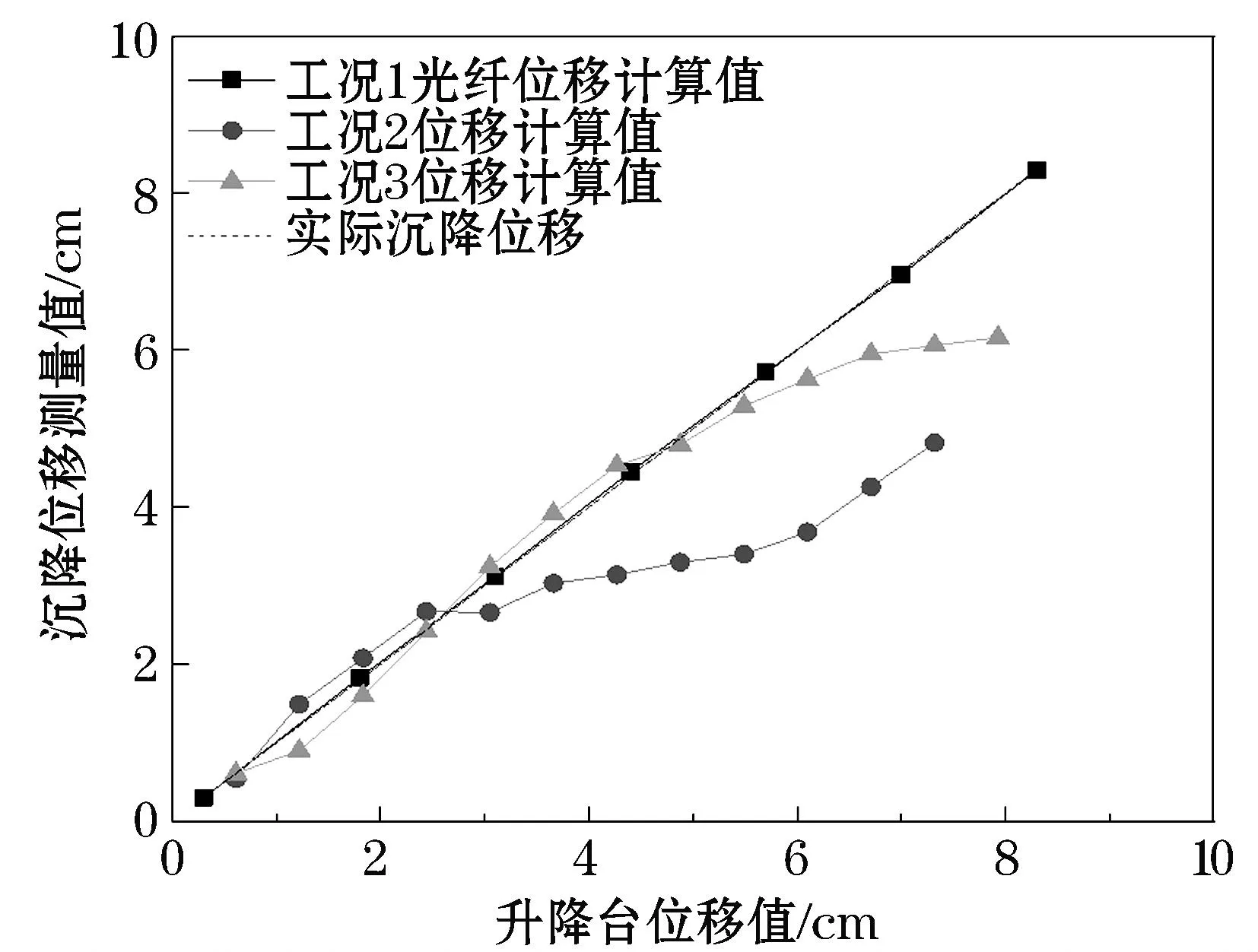
图6 各工况下沉降位移测量值与实际值对比图

3.2 光纤与土体耦合性分析

国内外的相关研究显示,直埋式光纤和周围土体的相互作用是一个相当烦琐的问题,光纤在土体沉降过程中的应变测量值和真实的土体变形之间有一定的应变损失,并且隐藏的影响因素众多,至今没有很好的解决方案.但是通过上述实验结果及分析可知沉降位移测量值与光纤和土体的耦合性相关.为此,本文提出纤-土沉降耦合变形系数K,定义为沉降位移测量值与土体实际位移的比值,用以表征光纤在伴随土体沉降过程中与土体之间的耦合性.结合式(7),K可以表示为:

(8)

其中:dN表示土体的实际沉降位移.

当土体发生沉降时,光纤随之沉降并被拉伸而产生应变.根据式(8)和测得的应变及位移数据,得到三种工况下光纤沉降系数K与实际沉降位移d之间的关系如图7所示.图7中的圆圈为沉降系数K的实验测量结果,K=1的水平实线为理想耦合线,表示沉降位移的测量值与实际沉降值相等.

图7 光纤沉降耦合系数随土体实际沉降位移的变化关系

对图7展开分析如下:

1) 纤-土耦合变形系数K值的大小可以反映出光纤与土体相互作用的效应,也可以用于判断光纤与土体耦合性的好坏.K值越接近于1,光纤与土体的耦合性就越高,监测到的光纤应变值就越准确.为了更好地分析土体纵向沉降位移逐渐增大时光纤与土体的耦合特征,根据耦合系数K值情况将耦合状态划分为纤-土耦合度良好阶段和光纤滑移阶段,如图7所示.其中在光纤与土体耦合度良好阶段,光纤和周围土体的耦合度高,沉降系数测量值与理想耦合线符合较好.在光纤滑移阶段,光纤应变分布受到多种因素的影响,如光纤两端固定点滑脱、土体沉降不均匀等,此时测量得到的沉降位移将不能很好地反映出真实的土体变形.

2) 如图7(A)所示,工况1在土体沉降过程中K值始终在1附近,耦合情况最为理想.对比图7(B)、(C)可以看出,工况2和工况3的K值变化趋势相似,都是前期耦合度良好,当实际沉降达到某一个数值后沉降位移测量值与实际位移值开始产生明显偏差,此时纤-土耦合变形系数骤降.这是由于这两种工况下光纤周围有土压存在,随着沉降位移的增大,光纤会产生滑移.但是可以清楚地看到,工况2在沉降位移d=3.05 cm时其K值就进入了光纤滑移阶段,除了个别点K值较大之外,其余位置明显降低,这是由于工况2中的光纤没有固定地锚,光纤的沉降完全靠土体下沉作用;而工况3由于设置了地锚,土体带动地锚沉降的同时就会带动光纤移动,因此在沉降位移d=5.49 cm时其K值才开始进入光纤滑移阶段,说明地锚增大了光纤与土体之间的耦合面,从而增加了沉降位移的测量范围.

综合以上分析得到了如表2所示的纤-土沉降耦合变形程度划分标准,可以用于定量评价土体沉降过程中光纤与土体的耦合程度.

表2 实验所得纤-土沉降耦合变形程度划分标准

4 结 语

本文利用高空间分辨率BOTDA技术对土体沉降进行了监测研究,综合考虑了土体沉降变形、地锚固定等因素对纤-土沉降耦合变形效应的影响.通过沉降位移监测实验测量了三种不同情况下直埋式光纤的应变分布,结合应变-位移计算模型得到了相应的沉降位移,并将测量结果与实际沉降情况进行了对比分析.

为表征光纤在位移过程中与土体的耦合程度,提出了纤-土沉降耦合变形系数K,并根据其取值情况将土体沉降过程划分成两个阶段.在纤-土耦合度良好阶段,沉降位移的测量值与实际值符合较好.当土体的沉降位移增大到一定程度时,K值显著减小,即光纤和土体之间的耦合度降低,处于光纤滑移阶段(即光纤发生滑脱),此时根据光纤应变测值无法准确计算土体的沉降位移.此外,通过布设地锚能够增强光纤与土体之间的耦合效果,从而增大沉降位移的测量范围.