分数阶CEV模型下亚式期权的显-隐差分格式
2023-12-20孙玉东
龙 敏, 孙玉东
(1.贵州民族大学 数据科学与信息工程学院,贵阳 550025; 2.贵州民族大学 政治与经济管理学院,贵阳 550025)
亚式期权是如今较为流行的金融工具场外交易市场(OTC),它的收益取决于在某个特定时期的某种形式标的股票价格的平均值[1-2].主要是分为两种亚式期权:算术亚式期权和几何亚式期权.目前,算术亚式期权在OTC市场中变得越来越普遍.Kernna和Vorst[3]提出了算术亚式期权定价策略,后续也有很多解决算术亚式期权定价的方法,CEN Z等[4-5]人将有限差分方法作为一种数值方法去考虑亚式期权定价模型,再分析该方法的时间精度和空间精度.大多数已发表的文献都假设标的股票遵循对数正态分布过程,而Black-Scholes的基本假设模型是有一些缺点的.实证研究已经表明股票价格通常不太可能呈对数正态分布,当Black-Scholes模型用于为股票期权定价时会存在一些偏差,比如执行价格偏差和波动率微笑,这两者之间存在负相关股票价格变化和波动性变化.由Cox[6]开发的CEV期权定价模型就包含了这个负相关关系,将CEV模型应用于算术亚式期权是有意义的.
时间分数阶期权定价模型是金融工程中期权定价的一个重要数学模型.近年来,该模型的研究有很多的进展,其中大多数研究是在基于分数阶的情况下去求解各种期权的定价模型[7-9].关于讨论扩散方程的稳定性和收敛性的方法有很多,CHEN等[10-11]人通过傅立叶分析进行了讨论一种具有四阶空间精度的数值方案的稳定性、可解性和收敛性.在扩散方程[12-14]上讨论有限差分法的稳定性和收敛性的方法也很有用.关于B-S模型下股票期权定价时会存在一些偏差,有其他的研究方法是基于CEV模型下对期权进行定价.Peng Bin和Fei Peng[15]讨论了当标的股票遵循常数弹性(CEV)时的算术亚式期权定价过程,建立了一个二叉树方法来估计CEV过程,并用它来定价算术亚式期权.张增林等人[16]做利用二叉树逼近方法得到在CEV过程且有离散红利支付的标准几何亚式期权的定价.杜雪樵等人[17]在标的资产服从CEV模型下,推导出两值期权的定价式.孙玉东等人[18]在CEV风险资产模型下利用了有限差分算法研究触发式理财产品定价问题.彭斌[19]是利用了风险中性定价方法,推导出标的资产服从CEV扩散模型下领子期权的解析定价式.姜晓晴[20]是抽取一些上证50ETF期权交易数据,基于B-S模型与CEV模型,对上证50ETF期权定价.
鉴于此,本文考察时间分数阶CEV模型下算术亚式期权的显-隐和隐-显式差分格式的可行性.首先,用时间分数导数和中心差分离散空间导数得到了高精度的显式差分格式和高精度的隐式差分格式.其次,在这基础上构造显-隐和隐-显式差分格式,利用Fourier方法和数学归纳法验证其差分格式的稳定性和收敛性.最后,通过数值模拟证明了该差分格式对求解时间分数阶CEV模型下算术亚式期权是可行性的.
1 显-隐(E-I)式差分格式的构造及其数值分析
1.1 显-隐(E-I)式差分格式的构造
本节在固定敲定价格的时间分数阶CEV模型下算术平均亚式期权的偏微分方程下,将高精度的显式差分格式和高精度的隐式差分格式进行交叉运用得到本文所研究的显-隐式差分格式[8,13-14].时间分数阶CEV模型下算术平均亚式期权定价U(t,S,I)的偏微分方程[8]为
(1)
其中:r为无风险利率,σ为波动率,T为到期日,E为执行价格,α(0<α<1)是分数阶阶数,a(0≤a≤2)是一个常数因子(弹性因子),I(t)表示路径因子[1](标的资产价格运行总和)

对式(1)中的时间变量和空间变量进行等距网格划分,令
τj=jΔt,j=0,1,2,…,N;
xi=ih,i=0,1,2,…,M.
其中:Δt=T/N和h=X/M分别表示时间步长和空间步长,再对时间变量进行离散,为了提高差分精度选择中心差分格式
时间分数阶在点(τj,xi)的主方程式为
(2)
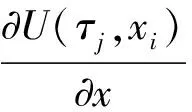
(4)
其中:差分算子为
时间分数阶导数在点(τj,xi)的离散格式为[11]
(5)

(6)
再对式(6)关于x求偏导数并化简有
(7)
(8)

(9)
其中:mk=(k+1)1-α-k1-α同样,将式(5)、(6)代入古典隐式差分格式(4),并进行化简得到高精度的隐式差分格式为
(10)
忽略截断误差,时间分数阶CEV模型下算术亚式期权的显-隐式差分格式构造如下:
求奇数层时,运用高精度的显式差分格式计算:
(11)
求偶数层时,运用高精度的隐式差分格式计算:
(12)
(13)
将上式化为矩阵形式为
(14)
其中:Gi(i=1,2,3,4,5)是(M-1)×(M-1)的矩阵,
1.2 显-隐(E-I)差分格式的稳定性
本节考察所上节得到的显-隐式差分格式(11)~(12)的稳定性[10-11].由式(16)可以得到以下几个结果:当e<0,f>0,g<0且满足e-|f+g|>0时,则矩阵G1是严格对角占优矩阵;当|G1|≠0时,G1是可逆矩阵,则系数矩阵G1为非奇异矩阵.当e′>0,f′<0,g′>0时,且有|G2|≠0,则系数矩阵G2是可逆矩阵,且G2又非奇异矩阵,故格式解是存在唯一解的.
根据文献[12],并结合上述两个结果可得到以下的两个结论,这些结果在之后的证明过程中也会被用到.
引理1时间分数阶CEV模型下算术亚式期权的显-隐式差分格式(11)~(12)的解是存在唯一的.
引理2[12]运用函数m(x)=x1-α(x≥1)的性质,得到如下结论
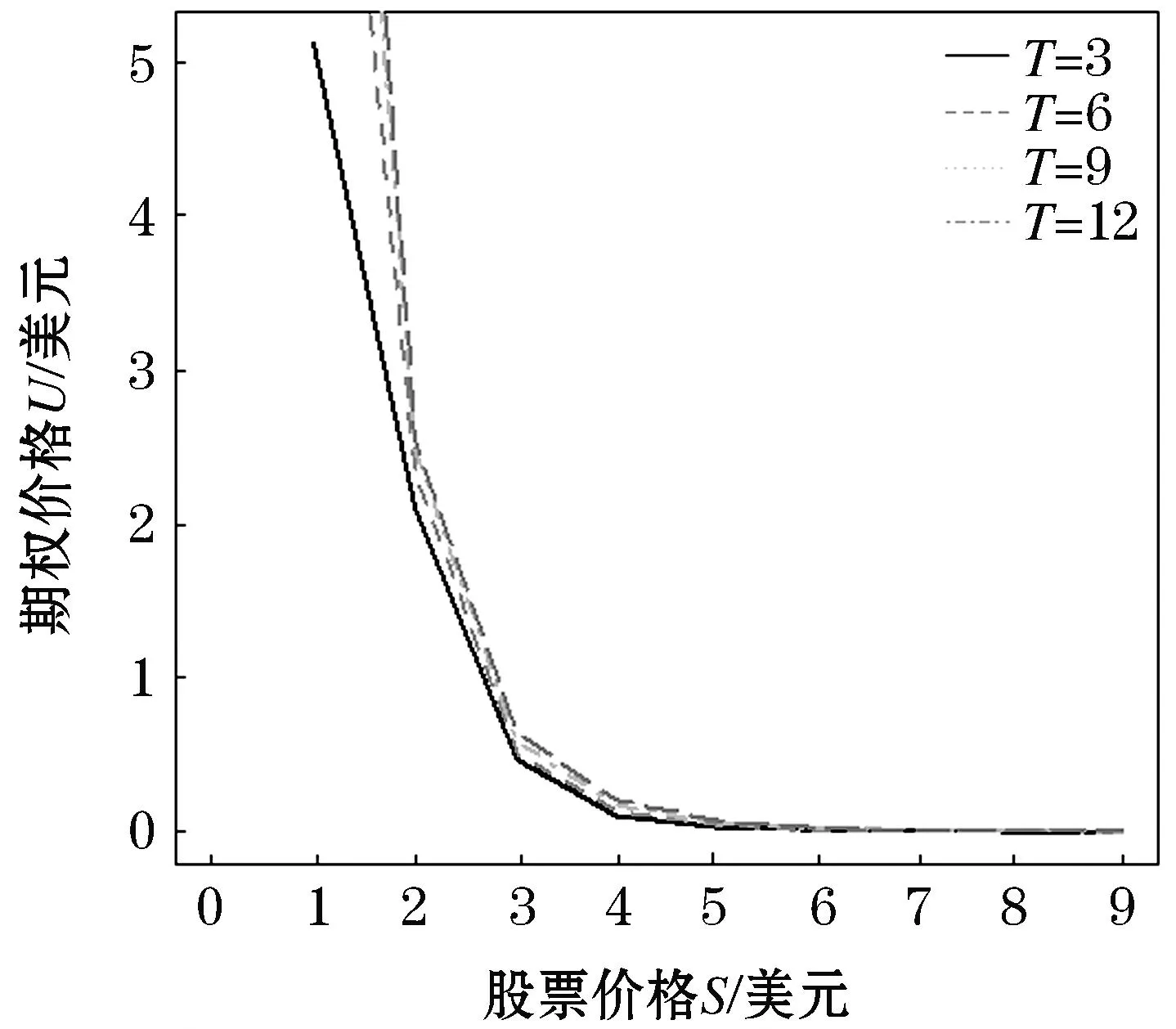
0 定理1在时间分数阶CEV模型下算术亚式期权的显-隐式差分格式(11)~(12)关于范数无条件稳定. 对εj(x)进行Fourier方法展开,使得 由Parseval定理有 (15) 基于以上的分析,可设方程的误差解的形式为 (16) 由exp(±iλh)=cosλh±isinλh经过变换后为 (17) 当s=1时,运用高精度的显-隐式差分格式中的高精度显式差分格式,可得 把误差解式(16)代入上式计算得 上式通过式(17)的两个变换运算,易知 利用引理2对上式进行不等式放大技术计算,可有 其中:C表示任意的一个正整数,在不同的情况下可以取不同的值. 当s=2时,运用高精度的显-隐式差分格式的高精度隐式差分格式,可得 将式(16)代入上式计算得 上式通过式(17)的两个变换运算,易得 通过引理2对上式进行不等式放大技术计算,可有 即|μ2j+1|≤C|μ0|.由式(15)和以上分析,可总结出 |εj|≤C|ε0|,j=0,1,…,N-1. 从而命题结论成立.证毕. 在本节中,将利用CHEN等[10-11]人证明差分格式收敛性的方法来考察所得的显-隐式差分格式(11)~(12)的收敛性. 证明:定义两个网格函数 对ηj(x)和Rj(x)进行Fourier方法展开,可有 分别定义ηj(x)和Rj(x)的范数为 由Parseval定理得 基于以上的分析,可假设 (18) 当s=1时,运用高精度的显-隐差分格式的高精度显式差分格式,易知 将式(18)代入上式计算得到dζ1=Δtαr1,通过引理2和引理3对上式进行不等式放大技术运算,可有 当s=2时,运用高精度的显-隐式差分格式的高精度隐式差分格式,易知 将式(18)代入上式计算得到 上式通过式(17)的变换后为 通过引理2和引理3对上式进行不等式放大技术计算,使得 综上所述,可得 关于ηj有, 从而命题结论成立.证毕. 本节主要构造隐-显式差分格式[13-14],并考察该格式的稳定性和收敛性.隐-显式差分格式和显-隐式差分格式大致相同,只是在奇数层和偶数层时选择了相反的差分格式.隐-显式差分格式在奇数层上,采用高精度的隐式差分格式计算: (19) 求偶数层时,运用高精度的显式差分格式计算: (20) 将式(19)、(20)进行相加消除,化简得 (21) 根据上节显-隐式差分格式的数值分析,可以类似证明过程得到隐-显式差分格式的如下的数值分析. 推论3 在时间分数阶CEV模型下,算术平均亚式期权高精度的隐-显式差分格式(20)~(21)存在唯一解. 推论4 在时间分数阶CEV模型下,算术平均亚式期权高精度的隐-显式差分格式(20)~(21)关于范数无条件稳定. 推论5 在时间分数阶CEV模型下,算术平均亚式期权高精度的隐-显式差分格式(20)~(21)关于范数无条件收敛, 其中:收敛阶为O(Δt2-α+h4). 本节主要考察隐-显式差分格式的相关数值分析,可类似于高精度的显-隐式差分格式分析过程,因为它们只是在偶数层和奇数层上使用的显、隐式差分格式刚好相反,所以隐-显式差分格式的稳定性和收敛性的证明过程和显-隐式差分格式大致相同. 本节主要以高精度的显-隐式差分格式(14)为例,运用R软件对其进行数值试验,检验该格式的可行性.基于表1中的参数,运用高精度的显-隐式差分格式(14)计算出算术平均亚式期权的价格,并绘制出股票价格和亚式期权价格的变化曲线图. 表1 模型参数 设在T=6,α=2/3的情况下,不同的弹性因子a(分别取a=1/2,1,3/2,2)绘制出股票价格与期权价格的变化趋势,见图1.当弹性因子a取不同的值时,观察到在股票价格为4之后,期权价格的变化逐渐趋于一条线.当a=2时是Black-Scholes模型下的时间分数阶亚式期权,在股票价格为2时股票价格下降较快.然而在整体上股票价格与期权价格的变化趋势大致相同.说明所得的高精度的显-隐式差分格式是可行的. 图1 不同a取值下亚式期权价格 在a=2,α=2/3下,根据不同的到期日参数T(分别取T=3,6,9,12)绘制出股票价格与亚式期权价格的变化趋势,见图2.随着T的不断增加,在股票价格为2时期权价格有较大的增加改变趋势,但是在整体变化趋势也基本一致. 图2 不同a取值下亚式期权价格 设a=2,T=12,根据不同的分数阶参数α(分别取α=1/3,1/2,2/3,1)绘制出股票价格与期权价格的变化趋势,见图3.α为分数阶和整数阶(α=1)时的股票价格和期权价格的变化趋势大致相同,下降趋势在股票价格为2和3时发生了改变.整体的变化趋势也基本一致. 图3 不同α取值下亚式期权价格 本节根据所研究的高精度显-隐式差分格式,选取了不同的弹性因子a、到期日T和时间分数阶α.观察这3个参数分别得到的股票价格与期权价格变化趋势图1~3,可以看出由各参数取值不同股票价格与期权价格变化趋势基本一致,从图3也可以看出分数阶和整数阶的亚式期权价格的变化趋势相似.从而可以得到数值模拟的结果与理论分析相符,用本文所得到的差分格式去解决此类的问题可行. 本文运用高精度显-隐式差分方法研究了时间分数阶CEV模型下亚式期权定价问题.首先,利用时间分数导数和中心差分离散空间导数得到了高精度的显式差分格式和高精度的隐式差分格式,在求奇数层时运用高精度的显式差分格式,偶数层时运用高精度的隐式差分格式,即可得到显-隐差分格式,相反的做法可得到隐-显差分格式.其次,利用Fourier方法和数学归纳法分析该差分格式的稳定性和收敛性.最后,通过R软件进行数值模拟,模拟得到的结果和理论相符,说明本文所得到的显-隐差分格式和隐-显差分格式对求解时间分数阶CEV模型下算术亚式期权可行.

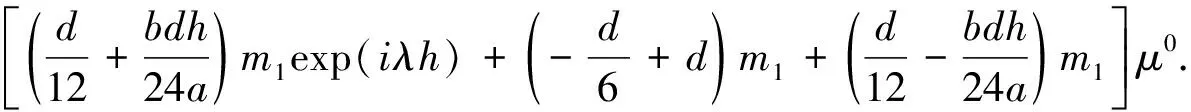
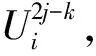
1.3 显-隐(E-I)差分格式的收敛性

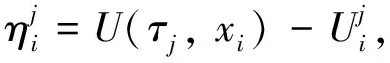
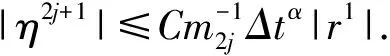

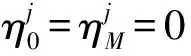
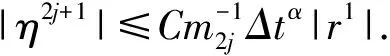
2 隐-显(I-E)差分格式及其数值分析
3 数值模拟



4 结 语
