基于线索KD-Tree的射线追踪并行计算

厉夫兵，苏永琪，陈文剑

(1.北京信息科技大学 信息与通信工程学院，北京 100101； 2.哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨 150001)

0 引 言

射线追踪法[1]在通信与计算机领域具有很广泛的应用。通信领域中，利用射线追踪法可以分析目标的散射特性。计算机领域中，通过射线追踪可以使二维平面图像呈现更真实的三维效果，常用于图像渲染。空间剖分技术和并行计算可以运用于射线追踪计算过程中，解决射线追踪效率低下的问题。1980年J. Bentley提出KD-Tree空间剖分技术，已被运用于射线追踪静态场景的计算中，旨在将射线追踪计算过程的时间复杂度降低[2，3]。此外，随着GPU架构技术的不断发展，GPU逐渐展现出了强大的并行计算能力。NVIDIA公司提出的统一计算设备体系结构(CUDA)[4]作为开发环境，可以将大量数据进行合理分配后，交由GPU进行并行计算。射线追踪过程中会面对大量射线数据，因此GPU并行计算可以有效提高射线追踪计算效率。

本文针对传统射线追踪计算效率低下的问题，首先对目标场景进行三角剖分建模，其次采用KD-Tree数据结构对场景空间进行合理划分，并且通过添加线索指针的方式实现KD-Tree的无堆栈遍历，以此避免大部分无效的求交运算[5]，最后在CUDA平台下设计射线追踪在CPU-GPU异构计算的实现方案，合理分配计算资源，将射线追踪过程并行化[6]。通过KD-Tree与并行计算结合，改善射线追踪的计算时间。

1 KD-Tree的创建

KD-Tree是二叉空间剖分树的一种，它是利用平面的定策性质，使用一个平面将目标模型的空间划分为两部分，之后再递归地对已经划分好的空间进行分割，直到达到提前设定的条件[7]。

目前构建KD-Tree的一种方法是通过表面积启发式(surface area heuristic，SAH)[8]选取合适的剖分面，递归将目标场景剖分为若干个轴对齐长方体包围盒。但当包围盒内三角面元数量较多时使用SAH算法计算代价值会出现误差，因此本文结合目标空间每一维度的方差与维度上面元坐标的中心点来确定剖分的维度与剖分面。创建KD-Tree的具体步骤如下：

(1)基于仿真模型上的三角面元和节点信息构建包围盒，作为KD-Tree的根节点。

(2)选取合适的分割轴与剖分平面，切割根包围盒生成左右子节点。为选择合适的分割轴，需要计算节点内各个面元的中心点坐标分别在x，y，z维上的方差。任一维度方差的计算公式如式(1)所示

(1)

式中：centeri表示某一维度上的每个面元中心点坐标的值，mean表示某一维度上所有面元中心点坐标的平均值，FaceNumberInNode表示当前节点内三角面元的数量。

在确定分割轴后，可以对分割维度上三角面元的中心点进行排序，选取中间值作为剖分面。

(3)对于新生成的节点重复步骤(2)的内容，直到节点内的三角面元数量达到提前设定的阈值，节点不可再分割。

自此，KD-Tree构建完成，剖分过程中所形成的节点是KD-Tree的中间节点，剖分结束后的不可再分割节点是KD-Tree的叶子节点。

腔体模型的剖分示例和分割模型生成的KD-Tree如图1所示。根包围盒为N0，面L0将N0切割为N1，N2两个节点，面L1，L2分别将N1，N2切割为N3，N4，N5，N6这4个节点，为节省内存开销，在将节点分割后将模型的面元信息与点信息都保存至生成的子节点中，因此最终模型的信息都会保存在叶子节点中[9]。由于模型剖分的密度不同，每次切割并不能保证左右子节点中的面元数量相同，因此每个叶子节点中的三角面元的数量会随着剖分的不同而不同。对于完全处于包围盒内的面元，如图1(a)中的2号与4号面元，它们分别只属于N4，N5节点；而对于属于分割平面上的面元，例如1号面元既属于N3节点又属于N4节点，3号面元既属于N5节点又属于N6节点。

图1 模型分割及二叉树生成

2 KD-Tree的遍历

2.1 KD-Tree节点线索的生成

为实现KD-Tree的无堆栈遍历，本文通过线索指针的方式建立节点之间的索引。Popov等提出了一种KD-Tree的线索创建算法，该方法现常被用于KD-Tree的无堆栈遍历[10]，文献[11]根据其算法思想进行了一定程度的简化与改进，提出了一个节点间线索建立算法。“线索”实际上是KD-Tree节点之间的指向关系。线索建立的过程分为“继承”和“更新”，“继承”是指节点首先要继承其父节点的所有线索信息，“更新”是指更新节点分割轴方向上的指向关系。平面包围盒剖分结果及射线过程如图2(a)所示，下面通过图2(a)介绍传统与改进后建立线索的方式。以3号与6号节点为例，通过传统方式建立线索时，3号节点首先继承其父节点1号节点的线索信息，即x轴正向索引(以下简称x+)、x轴负向索引(以下简称x-)、y轴正向索引(以下简称y+)、y轴负向索引(以下简称y-)均为NULL，其次由于1号节点的分割轴为x轴，因此根据包围盒的位置关系将3号节点的x-更新为2号节点，至此3号节点线索信息更新完毕；6号节点首先继承其父节点3号节点的线索信息，即x-为2号节点，x+、y+、y-均为NULL；其次6号节点的父节点分割轴为y轴，所以将6号节点的y-更新为7号节点，6号节点的线索信息也更新完毕。

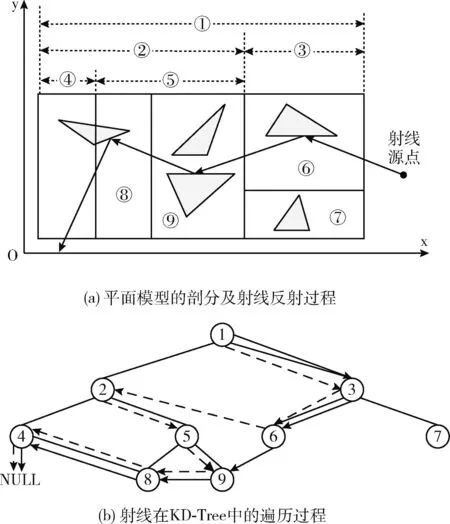
图2 平面模型中射线追踪路径

传统方式建立线索是在分割形成节点的同时就将节点线索随之建立，当其相邻节点再度进行分割后，分割信息无法及时反馈至先前节点中，因此无法达到最优的线索指向关系。改进后的方法优化步骤主要在“更新”的过程中，每个节点在建立线索时需要了解其相邻节点的完整分割信息，因此建立线索的过程需要在建树完成后进行。通过改进方法建立线索时，3号节点依旧要先“继承”1号节点的所有线索关系，在“更新”过程中，需要判断3号节点的兄弟节点(2号节点)的分割轴(x轴)与其父节点(1号节点)的分割轴(x轴)是否相同，若相同则将3号节点的x-更新为2号节点的右孩子节点(5号节点)，随后继续更新。更新完成的条件一是直到3号节点的x-为叶子节点，二是x-指向节点的分割轴与3号节点父节点(1号节点)的分割轴不再相同。由于5号节点的分割轴仍与1号节点相同，因此最终3号节点的x-更新为9号节点；6号节点直接继承3号节点索引，x-为9号节点，其余方向索引均为NULL，在更新过程中，由于6号节点的父节点(3号节点)的分割轴为y轴，因此将6号节点y-更新为7号节点，更新结束。

对比之下，传统方法建立线索时6号节点的x-指向的是2号节点，改进后6号节点的x-指向的是9号节点，改进后的方法得到了更优的线索指向。

2.2 KD-Tree的遍历过程

射线追踪的过程实际上是射线遍历线索KD-Tree寻找叶子节点并与节点内三角面元进行相交检测的过程。图2(a)演示了一条射线在平面模型中反射的路径示意：

(1)射线通过入射位置定位到6号叶子节点，再通过Moller-Trumbore方法与节点内部的三角面元遍历求交，求出交点后更新射线为反射射线[12]；

(2)反射射线确定出射位置后查找线索确定下一个待遍历节点为9号节点，遍历节点内面元求交，继续更新反射射线，并通过出射位置查找对应线索指向节点为8号节点，射线在8号节点内继续遍历；

(3)在8号节点内求得交点与反射射线后，射线进入4号节点中遍历后并未与节点中的三角面元发生相交，并且出射位置指向的线索为NULL，该条射线射出模型，遍历结束。

因此，单根射线遍历过程就是射线与叶子节点内面元求交后，通过线索信息查找到下一个待遍历的节点继续求交，直到射线在某节点出射位置的线索指向NULL时，遍历结束。射线在KD-Tree中的遍历过程如图2(b)所示，图2(b)中虚线(实线)表示传统(改进)线索建立方式下射线遍历线索KD-Tree的过程，由图可见，改进后明显减少了部分中间节点的遍历，节省了开销。

3 射线追踪并行计算

传统串行计算中，未进行追踪的单根射线需要等待在其之前的射线追踪完毕后，方可执行计算，而每根射线在与三角面元求交时都会产生巨大的时间开销，使得串行计算效率低下。单根射线在追踪过程中都是相互独立的，因此很适合采用GPU对射线追踪计算过程进行并行加速，提高计算效率。

3.1 CUDA并行编程模型

CUDA是一种CPU与GPU相结合的异构运算平台，它将CUDA C语言作为编程语言，并由CPU负责处理逻辑关系复杂的事务，GPU负责处理需要高度计算的事务。相应的，CPU一般被称作主机端(Host)，GPU一般被称作设备端(Device)[13]。在CUDA编程中，运行在GPU端的程序需要通过核函数(Kernel)“标识”出来。

核函数的启动需要调度网格(Grid)、线程块(Block)及线程(Thread)，这三者最高可组织为三维形式。三者二维类型的层次结构如图3所示：一个Grid中包含多个Block，一个Block中包含多个Thread[14]。其中Thread是执行计算的单位，因此并行计算的过程实际上是每个Thread各自执行Kernel的过程。

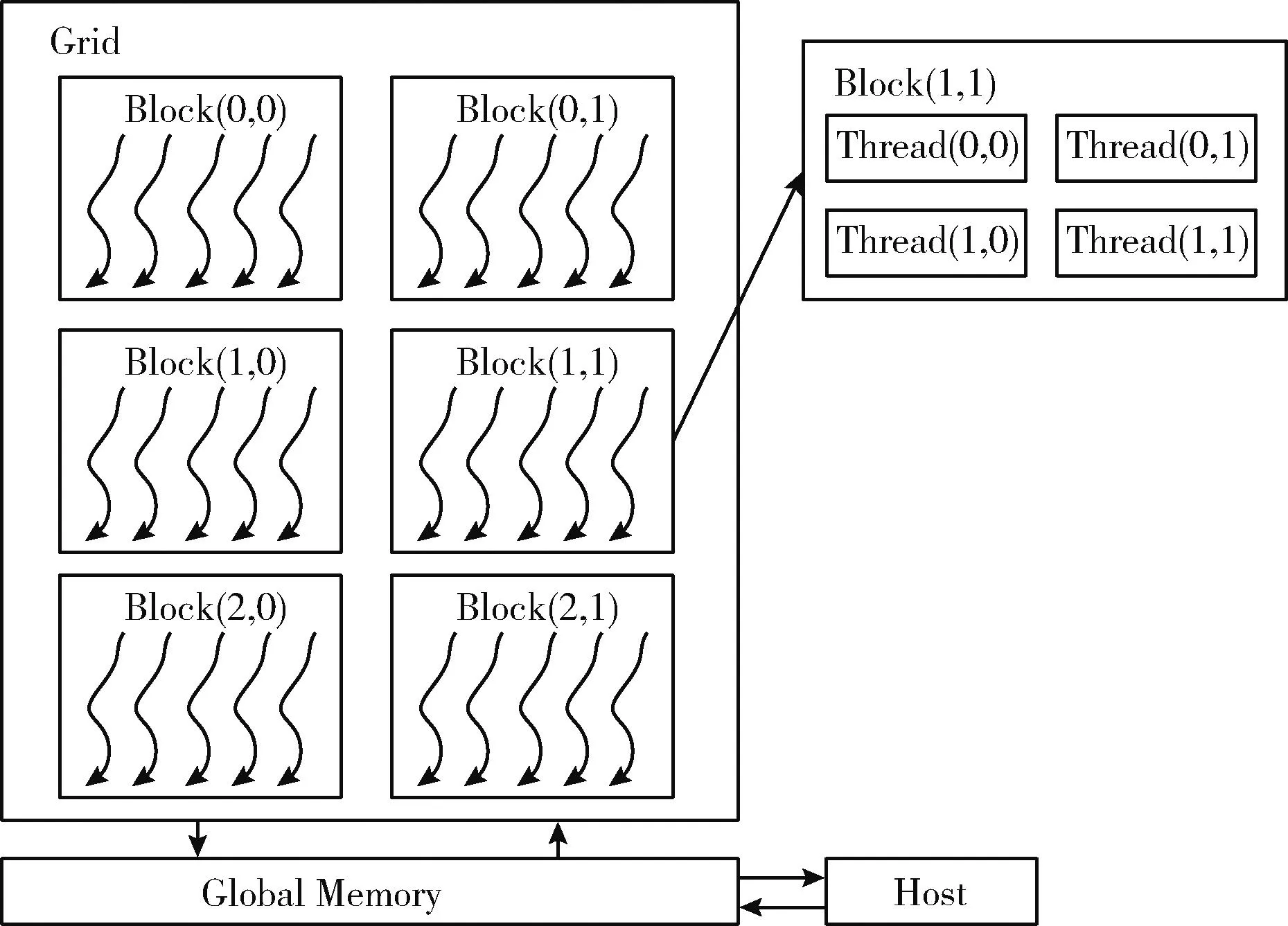
图3 CUDA线程层次结构

由于计算量的不同，在进行并行计算时需要选择合适的计算资源，即选取合适数量的Thread进行计算，程序层面上，通过线程块数量(BlockperGrid)指定执行计算的线程块数量，通过块内线程数量(ThreadperBlock)指定每个线程块中执行计算的线程数量，分配的线程总数量通过线程块数量与块内线程数量相乘得到。本文为进行并行计算资源的合理分配，设置线程总数量与射线的数量保持接近，由于一般情况下BlockperGrid和ThreadperBlock都设置为32的倍数，为同时满足这两个条件，一些情况下射线数量会略大于线程总数量，这时需要少数线程执行两根射线的计算过程。

CUDA架构可以调用GPU内存资源对数据进行处理，GPU内存包括全局内存、共享内存、常量内存、纹理内存等，各个存储器的位置与特性不都相同。由于共享内存读写速度快，但空间较小，而常量内存与纹理内存只能进行读操作，因此本文将数据全部存至设备端全局内存中，每个线程直接在全局内存中进行读写操作。

3.2 射线追踪并行化过程

串行计算的全部过程在CPU上执行，每条射线依次遍历线索KD-Tree计算其在场景中的传播路径。将串行计算程序改为并行计算程序一般有两种方法，一是整个过程直接由GPU完成，二是将需要高度计算的部分由GPU完成，其它的部分仍由CPU完成[15]。

在射线追踪过程中，每条射线在场景中进行弹射时是相互独立的，因此将射线追踪的计算过程进行并行化的核心思想是将单根射线分配至GPU的单个核心进行射线的路径计算，对射线追踪进行并行化实现的方案如图4所示，并行化过程中，构建线索KD-Tree的任务逻辑比较复杂，因此由CPU完成；而射线遍历线索KD-Tree的过程存在大量射线与节点内三角面元的求交计算，因此需要由GPU并行完成。

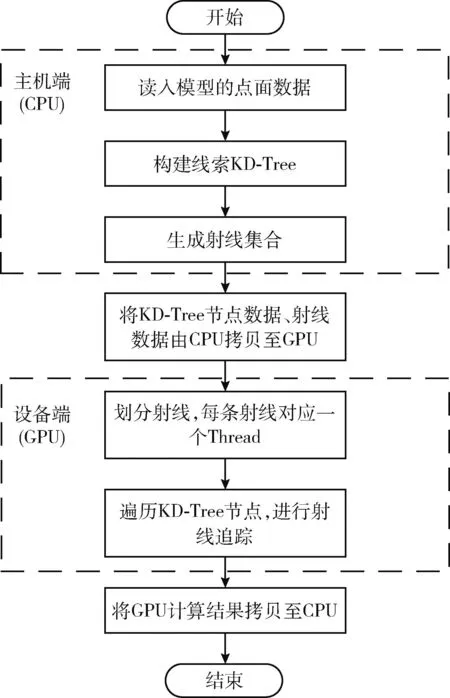
图4 射线追踪并行化实现方案

由于CPU与GPU无法互相直接读取存储在对方内存里的数据，因此需要进行数据传输以完成计算。需要传输的数据分为两部分：一部分是射线集合，一部分是线索KD-Tree节点。射线集合是预设条件，在CPU中静态存储，因此可以通过cudaMemcpy函数直接由CPU端拷贝至GPU端；本文在第1节末描述了构成模型的三角面元都将分别存储在各个叶子节点中，且剖分后每个叶子节点中面元数量并不相同，因此叶子节点指针需要动态分配内存，这造成KD-Tree无法直接通过cudaMemcpy函数进行传输，本文通过计算建树完成后每个叶子节点的内存信息，并在GPU端开辟相同大小的内存将其逐一拷贝，以实现叶子节点内面元数据的传输。而对于根节点和中间节点，由于其内的面元数据已被释放，因此仍按照静态存储方式进行拷贝。

数据传输完成后，由一个线程(Thread)负责一条射线的追踪，多条射线并行进行追踪，得到每条射线的弹射次数及每次反射时发生相交的三角面元编号，最终将计算结果回传至CPU。

4 仿真结果与讨论

本文实验数据通过一台计算机仿真得到，该计算机操作系统为Windows 10，CPU型号为Intel(R)Core(TM)i5-10210U CPU @ 1.60 GHz，GPU型号为NVIDIA GeForce MX350，编译环境为Microsoft Visual Studio 2019(CPU端)，CUDA toolkit 11.4(GPU端)。

为对算法有效性进行验证，本文模拟射线在T型腔内进行弹射，并对其轨迹进行追踪。腔体及发射源如图5所示，图5(a)为通过ANSYS Mechanical APDL 16.0对腔体表面进行三角网格剖分，剖分后三角面元总数为9478，图5(b)为腔体模型在y轴方向上的长度为4.5 m，x轴、z轴方向上的长度分别为通过1 m、0.5 m，腔体的3个开口面边长均为0.5 m。x轴方向上的腔体开口0.05 m处设置0.5 m×0.5 m的虚拟散点面，射线源点与散点面上的散点构成射线集合。射线可以通过出射面射出。实际应用中，射线一般是电磁波、声波等，多次反射后会有能量衰减，因此设置射线在腔体内的弹射次数最多不超过30次。

图5 腔体及发射源

表1对比了在射线数目为1500，KD-Tree树高为6，节点总数为63、其中叶子节点总数为32时，线索建立方式改进前后遍历节点数量的变化及串行、并行计算所耗费的时间，由表1可以看出，改进后的线索建立方式比改进前遍历节点数量减少了4832，减少了射线查找KD-Tree寻找叶子节点过程的开销。从运行时间上看，无论是串行计算还是并行计算，改进后算法的程序执行效率比改进前都有一定程度的提高。

表1 不同线索建立方式计算时间

实际情况中，运用射线追踪算法对目标进行特性分析时，为了得到精确的计算结果，往往需要发射大量射线进行追踪，因此本文讨论了射线数量成倍增长的情况下并行计算相比于串行计算的效率提升。当KD-Tree树高为6，线程块与块内线程数同为128，射线数目变化的情况下，CPU、GPU端的计算时间见表2。从表2中的时间及加速比可以得知，射线数目数量级增长时，加速效果越来越好，当射线数目达到十万数量级时，加速比达到20倍左右。实际场景中的射线数目往往更加巨大，因此，通过GPU并行计算得到的效率提升会越来越明显。

表3给出了在射线数目为15 000，线程块与块内线程数同为128时，KD-Tree构建不同时的程序运行时间，从表中可以看出，对于串行计算来说，树高越高程序运行速核度越快，这是由于CPU适合处理KD-Tree这类逻辑结构较强的事务，叶子节点数量越多，内部三角面元数量越少，射线遍历节点的速度越快；对于并行计算来说，GPU核心处理复杂逻辑事务的能力相比CPU较差，分支过多时，运行时间部分花费在遍历树寻找节点的过程中，但分支过少时又会有大量的无效求交计算，因此在树高太高、太低时都会对程序的执行效率造成影响。

表2 射线数目变化对运行时间的影响

表3 KD-Tree层高对运行时间的影响

函数参数配置对程序运行效率也有一定影响，合理的参数配置更容易使得资源得到合理利用。核函数参数配置主要体现在线程块数量(BlockperGrid)以及块内线程数量(ThreadperBlock)，表4是在射线数目为15 000、KD-Tree层高为6时，BlockperGrid和ThreadperBlock不同的情况下程序的运行时间。由表可知，当BlockperGrid和ThreadperBlock都设置为128时程序运行效果最好。其中ThreadperBlock对程序运行时间影响更大，这是由于线程是执行计算的单位，程序会将一些寄存器分配给每个线程，寄存器的读写速度比全局内存快，如果ThreadperBlock设置太大容易造成可分配寄存器数量不足，线程将从全局内存读取数据，全局内存的访问延迟高于寄存器因此会造成运行时间增多；而ThreadperBlock设置太小又会造成一些寄存器资源浪费，同样会对运行时间造成影响。

表4 核函数参数配置对运行时间的影响

5 结束语

本文首先介绍了一种KD-Tree线索建立方式，并进行了有效性验证，其次针对传统的基于线索KD-Tree的射线追踪串行计算进行并行化实现，并对改变前后的运行时间进行了对比，实验数据表明并行算法使得计算效率得到提高，计算时间大大减少，此外还探讨了KD-Tree的构建质量以及核函数参数的设置对于程序执行效率的影响。在以后的研究中，还需要考虑以下问题，GPU全局内存的读写速度相比于其它内存较慢，可以将模型数据在不同内存区进行合理的规划分配，进一步提高计算效率。