混合乌鸦算法求解带软时间窗的车辆路径问题

闫 龙，石小娟，唐 源

(山东工商学院 管理科学与工程学院，山东 烟台 264005)

0 引 言

1987年Solomon将顾客的时间窗约束引入VRP中，提出了带时间窗的车辆路径问题(vehicle routing problem with time windows，VRPTW)，此后的研究中也衍生出多种VRP变体问题[1-3]。时间窗约束可分为软时间窗约束与硬时间窗约束，软时间窗约束指物品需尽可能在顾客指定的时间窗内送达，否则将产生惩罚成本；硬时间窗约束规定若车辆无法在指定时间内将货物送达，则服务失败。在实际生活中，食物、生活用品等物流配送都可归结为带软时间窗的车辆路径问题。目前关于VRPSTW的求解多采用启发式算法，谢九勇等[4]研究了带多软时间窗的VRP，提出嵌套多邻域结构的禁忌搜索算法。夏扬坤等[5]采用改进禁忌搜索算法求解带软时间窗的超市配送问题。Xu等[6]构建了带软时间窗的多目标绿色VRP模型，提出改进非支配排序遗传算法。何美玲等[7]针对VRPSTW，设计了一种将变邻域搜索算法与蚁群算法结合的混合算法。Xia等[8]采用改进禁忌搜索算法求解开放式VRPSTW。符卓等[9]考虑软时间窗以及需求可依订单拆分的现实情况，设计了一种改进禁忌搜索算法。

综上可知，启发式算法可有效求解VRPSTW。乌鸦搜索算法(CSA)作为一种新型智能启发式算法，近年来已被成功应用于求解车间调度[10]、0～1背包[11]等优化问题，但将其用于求解VRP的研究较少。本文将乌鸦搜索算法与自适应大规模邻域搜索算法结合，提出一种混合乌鸦搜索算法(HCSA)，并将其应用于求解VRPSTW。通过3组仿真对比实验，验证了HCSA的寻优性能与有效性。

1 问题描述及模型构建

1.1 带软时间窗的车辆路径问题描述

(1)

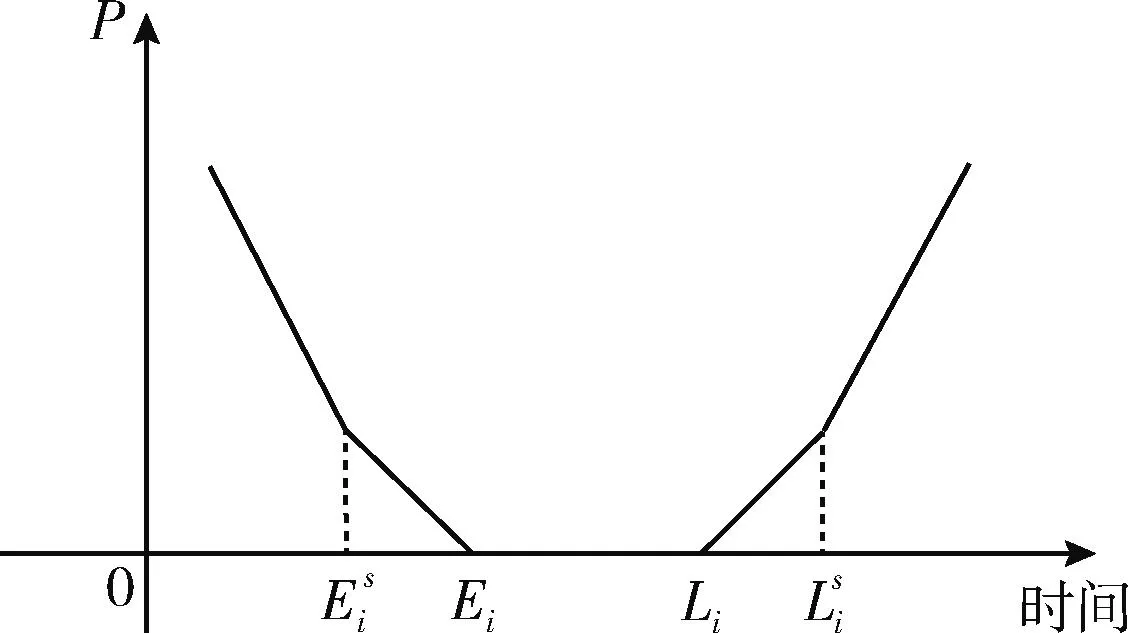
图1 折线软时间窗

1.2 模型建立

综上，以总成本最小为优化目标，建立如下数学模型

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

2 混合乌鸦搜索算法

乌鸦搜索算法同粒子群算法、蚁群算法、灰狼算法等群智能优化算法类似，通过模拟乌鸦寻找其隐藏食物的方式来搜寻求解问题的最优解。本文根据车辆路径问题的特征，采用基于顾客序列的整数编码方式对乌鸦空间位置向量进行编码，设计最短距离与最小惩罚两种初始化规则，并根据乌鸦的智能搜索行为，对其感知概率进行改进，提出一种基于自适应大规模邻域搜索策略的混合乌鸦搜索算法(HCSA)。

2.1 编码方式

本文采用基于顾客序列的整数编码方式对乌鸦搜索食物时的空间位置向量进行编码，假设顾客数目为10，则乌鸦i的空间位置向量即为10维的整数编码序列，如乌鸦i的位置为Xi=[4 8 9 7 1 3 2 5 10 6]， 在满足时间窗、载重量等约束条件的情况下可将其解码为加入配送中心0的超路径[13]向量Yi=[0 4 8 9 0 7 1 3 2 0 5 10 6 0]， 该向量即代表配送方案有3辆车，路径分别为 [0 4 8 9 0]、 [0 7 1 3 2 0]、 [0 5 10 6 0]。

2.2 种群初始化

本文设计了最短距离与最小惩罚两种初始化规则如下：

(1)最小距离成本初始化规则。车辆从配送中心出发，随机选择一个顾客a作为初始访问顾客，根据时间窗、载重量等约束条件进行访问可行性判断，将符合访问条件的顾客加入可访问列表V，从V中选取距离a最近的顾客作为下一个访问节点，直到所有顾客被访问完毕。

(2)最小惩罚成本初始化规则。同上所述，随机选择顾客作为初始访问顾客，依次计算该顾客可访问列表V中每个顾客的时间窗惩罚成本，选择惩罚成本最小的顾客作为下一个访问顾客，直至所有顾客均被服务。

2.3 乌鸦搜索行为设计

乌鸦被认为是最聪明的鸟类，它们会把多余的食物藏在隐蔽的地点，并在几个月之后还能回忆起食物的隐藏位置。此外，乌鸦还会观察其它乌鸦隐藏食物的地点，并跟随它们到达藏食之处，趁其它乌鸦离开之际偷走食物。假设乌鸦i决定跟随乌鸦j接近其隐藏食物的位置，则可能会出两种情况：①乌鸦j不知道被乌鸦i跟随。在这种情况下，乌鸦i将会跟随乌鸦j找到隐藏的食物。②乌鸦j知道被乌鸦i跟随。则乌鸦j为了保护它的食物不被窃取，会进入搜索空间的另一个位置以欺骗乌鸦i。这两种搜索行为可用式(11)来表示

(11)

(12)

其中，rj为[0，1]之间均匀分布的随机数，APj，iter表示乌鸦j在iter代的感知概率。这两种搜索行为分别对应于确定性搜索和随机性搜索两种搜索模式，两者之间的平衡主要由感知概率AP决定，较大的AP值可增加解的多样性，原算法中的AP为一个固定值，本文引入自适应调整策略，令AP=e-μ*iter/Mt， 该值会随着迭代次数的增加而变大，使得算法在前期倾向于全局随机性搜索，在后期则更可能采用局部确定性搜索，其中μ为自适应调整系数，改进后的公式如式(12)所示。对应于两种搜索模式，本文设计了6种确定性邻域搜索算子与4种随机性邻域搜索算子如下。

(1)确定性邻域搜索算子：①最大成本节约移除算子。依次计算移除每个顾客点i(i=1，2，…，n) 可节约的距离成本与时间窗惩罚成本之和costi，优先移除costi值最大的顾客点。②最大时间窗惩罚成本移除算子。依次计算每个顾客违反时间窗约束的惩罚成本，移除时间窗惩罚成本值较大的前Dr个顾客，Dr取顾客总数n的0.15～0.2[14]倍。③相似度移除算子。随机选择顾客点d作为参考节点，依次计算其它顾客与参考节点的相似度，优先移除相似度最大的顾客。相似度由两顾客是否在同一辆车、需求量、时间窗以及服务时间的相近程度决定，顾客j(j=1，2，…，n) 与d的相似度计算公式如下

(13)

(14)

④距离成本贪婪插入算子。随机选择顾客点c，判断并找出其所有可插入位置，计算顾客c插入到每个位置增加的距离成本，将其插入到成本增量最小的位置。⑤时间窗惩罚成本贪婪插入算子。依次计算选定顾客点插入到每个可插入位置的时间窗惩罚成本增加量，选择成本增量最小的位置插入。⑥全局最优成本插入算子。判断找出Dr个被移除顾客点的可插入位置，依次计算每个顾客点所有可插入位置的时间窗惩罚成本与距离成本增量之和，优先选择总成本增量最小的顾客点插入。

(2)随机性邻域搜索算子：①随机移除算子。随机选择Dr个顾客点加入移除列表R。②随机车辆移除算子。从当前解中随机选择一辆车，将整辆车的顾客作为移除点。③随机遗憾准则插入算子。每次从遗憾值最大的前y个顾客中随机选择一个顾客作为移除节点，遗憾值计算规则如下：依次计算每个可插入位置的距离与时间窗成本总和的增量，遗憾值即为前x个总成本增量次优值与最优值的差值总和。④随机贪婪成本插入算子。依次计算每个可插入位置的总成本(包括距离成本与时间窗惩罚成本)增量，从总成本增量最少的前r个位置中随机选择一个插入位置。

各算子权重自适应更新策略如下：设各算子的初始权重一致，若新解Xnew优于全局最优解，则加5分；若Xnew优于原解Xorign，加3分；否则不加分。设ωorign与ωnew分别代表算子原始权重与更新后的权重，θ为更新系数，ε为分数，π表示算子使用次数。权重更新公式如式(15)所示

(15)

2.4 算法流程

本文改进的混合乌鸦搜索算法(HCSA)的执行流程如下。

算法：HCSA

输入：最大迭代次数Mt，种群数量P，距离矩阵D，顾客位置矩阵L，车辆容量Q，顾客数目n，需求量d，时间窗TW，服务时间s。

输出：最优路径Xb。

(1)根据2.2节生成初始种群Xj，j=1，2，…，n， 计算每只乌鸦的适应度值f(Xj)，j=1，2，…，n， 初始化当前迭代次数t；

(2)whilet≤Mt

(3)foreach乌鸦

(4)Ifrand≤e-μ*iter/Mt

(5) 乌鸦采用确定性方法搜索食物，根据2.3节(1)ALNS(①～⑥)对食物所在空间进行自适应大邻域搜索；

(6)else

(7) 乌鸦随机选择空间中的位置，采用2.3节(2) ALNS(①～④)对解向量进行邻域搜索；

(8)endif

(9) 计算经过邻域搜索后乌鸦的适应度值f(Xnew)，iff(Xnew)

(10)endfor

(11)记录每次迭代的最优解，将其加入G(i)(i=1，2，…，n) 列表；

(12)更新乌鸦种群位置，t=t+1；

(13)根据G(i)列表判断，当迭代停滞次数s_num>u时，停止迭代；

(14)endwhile

3 算例分析

3.1 参数设置

HCSA的各相关参数设置如下：最大迭代次数Mt=500，种群数量P=100，感知概率AP=0.5，各因素A、B、C、D的权重均设为0.25，y=n/2，x=3，r=n/2，更新系数θ=0.3，自适应调整系数μ=4，终止迭代次数u=Mt/5；目标函数中的参数值与文献[12]一致：违反时间窗惩罚系数p1=1，p2=0.5，p3=1.5，p4=2，顾客的容忍水平β=0.5，单位车辆固定启用成本C1=60，单位距离成本C2=8。

3.2 实验及结果分析

为验证HCSA的性能，本文采用不同算例进行3组仿真对比实验，所有实验均应用MATLAB编程进行求解。

(1)实验1：本组实验的算例选自文献[7]，文献[7]从Solomon 经典算例包含的6种不同类型算例C1、R1、RC1、C2、R2、RC2中各选取一例，并考虑25、50、100这3种客户规模。将本文提出的HCSA与何美玲等[7]提出的IACO进行对比分析，结果见表1～表3，其中GAP值表示HCSA与IACO相比较的优化率，GAP=100%×(HCSA所得最优解-IACO所得最优解)/IACO所得最优解。

表1 25个顾客点的算例求解结果

表2 50个顾客点的算例求解结果

表3 100个顾客点的算例求解结果

由上表可以看出，顾客规模为25、50的算例求解结果中，2/3的GAP为负值，顾客规模为100的求解结果中，所有GAP值均为负数；在所有算例中，5个算例的优化率超过30%，C201(100个顾客)算例的优化率则达到47.24%；综上可知，HCSA的求解结果优于IACO，具备较强的寻优能力，可有效求解小、中及大规模算例。

(2)实验2：采用文献[12]提出的软时间窗问题算例，将本文提出的HCSA与文献[12]的超启发式遗传算法、文献[15]的改进蚁群算法进行对比，结果见表4。GAP为HCSA与其它算法相对比的总成本优化率，GAP=100%×(HCSA所得最优解-各算法所得最优解)/各算法所得最优解， 3种算法求解的最优配送路径如图2所示。

表4 不同算法结果对比

图2 各算法最优配送路径

从表4可以看出，HCSA求得的总成本值最小，相比文献[12]的超启发式遗传算法与文献[15]的改进蚁群算法分别降低了13.58%、0.96%；HCSA所得方案相比于文献[12]车辆数减少了一辆，车辆装载率小幅提升；文献[15]求得的车辆数少，车辆装载率高，但每辆车的行驶距离过长，导致配送方案的距离成本过高，从而拉高了总成本值。综合对比显示，本文所提HCSA求得的配送方案更优，算法优化性能更强。

(3)实验3：采用本文的模型与算法，选取Solomon算例中具有100个顾客点的时间窗较窄的C1型算例与时间窗较宽的C2型算例进行求解，求解结果见表5、表6，其中BKS代表已知最优解。

由表5、表6可知，在C1、C2型共17个标准算例中，13个算例求得的车辆数与距离值与最优解一致，算例C103、C104、C207、C208的车辆数达到最优，且距离值与最优解相差较小，由此验证HCSA的优化性能与有效性，表明其具备求解大规模VRP的可行性。

表5 C1型算例求解结果

表6 C2型算例求解结果

4 结束语

本文研究了带软时间窗的车辆路径问题，首先考虑车辆固定启用成本、距离成本以及时间窗惩罚成本建立以最小化总成本为目标的数学优化模型。其次提出一种混合乌鸦搜索算法，设计两种种群初始化规则，根据乌鸦在搜索食物时的不同搜索模式，对其感知概率进行自适应调整，将乌鸦搜索算法与ALNS结合，设计了5种邻域破坏算子与5种邻域修复算子。最后，与已有文献算例结果的对比显示HCSA求得的总成本更低，求解结果更新了部分算例的最优解；HCSA可求得部分Solomon标准算例的最优解，验证了算法在求解大规模VRP上的有效性。由此表明HCSA可有效求解VRPSTW，未来可尝试应用于求解其它组合优化问题。