基于DRHOSVM的复杂结构瞬态可靠性分析
2023-12-20殷锐费成巍
殷锐,费成巍
(1.西安明德理工学院智能制造与控制技术学院,陕西西安 710124;2.复旦大学航空航天系,上海 200433)
0 前言
可靠性分析对复杂结构的优化设计和可靠运行至关重要。复杂结构是机械关键部件不可缺少的,其性能受恶劣的工作环境和复杂的载荷条件的影响。 由于高维不确定因素,复杂结构在瞬态极值输出响应阶段容易出现故障,影响机械的使用性能。为了保证机械的安全,有必要进行复杂结构受高维输入参数影响时的瞬态可靠性分析。
根据结构可靠性分析国内外现有进展,可将其研究方法分为数值模拟法、近似解析法和代理模型法。数值模拟方法主要涉及随机抽样[1-3]和重要度抽样[4-6]。 随机抽样方法广泛应用于分析结构可靠性,在随机失效中也应用广泛。 然而,由于大量样本函数的局限性,随机抽样方法所消耗的计算成本难以承受。 在重要性采样方法中,可以将原始概率密度函数替换为重要性采样密度函数,以减少样本数量[7]。 由于难以在高维空间中构建合适的ISD函数以及时变特征,该方法的应用范围仍受限。因此,数值模拟方法的可行性在复杂结构瞬态可靠性分析中较低。
在近似分析方法中,矩方法因可接受的精度和效率而被广泛应用于可靠性分析,包括一阶和二阶矩法[8-11]和点估计方法[12]。但近似解析方法不适于解决功能函数未知的可靠性问题,且可靠性分析方法可能会产生涉及高度非线性功能函数的不稳定解。因此,在复杂结构函数未知的情况下,近似解析方法的应用也受到限制。
代理模型方法的出现有效克服了数值模拟法和近似解析法的不足,为结构瞬态可靠性分析开辟了新的研究方向[13-16]。其中,支持向量机 (Support Vector Machine,SVM)是一种广泛应用的回归代理建模工具。 SVM 回归的主要思想是在拟合层上拟合尽可能多的样本,同时限制边缘违反程度[17-18]。由于最小化回归误差和自动选择机制的特性,它对于复杂的中小型数据集的可靠性分析更有效率。韩彦彬等[19]提出了一种在柔性机构中进行高效、高精度动态可靠性分析的SVM回归极值方法。HU等[20]提出了一种新的一类 SVM 回归方法来适应偏差约束。在结构概率的分析中,由于需要考虑不同且多样的运行载荷,导致数据样本稀疏,在高维输入参数的情况下计算困难。在这种情况下,降维(Dimension Reduction,DR)策略是缓解维数灾难的重要途径。DR方法包括线性DR和非线性DR。在线性DR方面,LIU等[21]探索了一种基于主成分分析的全局代理模型技术。 KIM等[22]开发了线性判别分析来获取基于广义LDA方法的多类分类器。线性DR虽然可以提取主要信息,但难以处理大计算量和混合数据。在非线性DR中,DAS NEVES CARNEIRO和CONCEIÇO ANTNIO[23]提出了基于Sobol′指数近似局部解的不确定空间解析降维技术,以解决可靠性的鲁棒设计优化问题。ZHOU、PENG[24]提出了一种结合核主成分分析(Kernel Principal Component Analysis,KPCA)和高斯过程回归代理模型的可靠性方法。与线性DR方法相比,非线性DR方法由于流形和核方法的存在,可以有效处理高维数据的分布问题,从而提高计算效率和降维效果。因此,可采用非线性DR对高维参数下的复杂结构数据集进行降维分析,以提升SVM在高维数据集的应用效率。
SVM模型的效率和精度主要由模型中的超参数决定。为了优化相关的超参数,许多学者研究了智能优化算法。JIA等[25]利用粒子群优化算法改进了SVM核函数的参数,以获得最高的识别和定位精度。HESAMI、 JONES[26]基于遗传算法(Genetic Algorithm,GA)提出了SVM-GA来优化SVM模型。ZHOU等[27]通过灰狼优化、鲸鱼优化算法和飞蛾火焰优化3种算法优化SVM模型的超参数。从以上研究来看,智能优化算法与传统的支持向量机相比确实提升了性能。然而,智能优化算法存在一个可改进的缺陷,即得到的优化值容易陷入局部优化。在某些情况下,局部最优解比全局可行解表现更差,导致SVM 性能降低。因此,迫切需要开发一种新的优化策略来寻找最优参数并提高准确性和效率。
针对上述结构可靠性分析问题,本文作者提出一种新的代理建模方法,即基于降维策略的参数优化支持向量机算法(Hyperparameters Optimization Support Vector Machine-based on Dimensionality Reduction,DRHOSVM)。 DR策略以保持高低维线性关系为约束,将大规模输入变量嵌入高维空间,拓宽传统支持向量机的高维使用范围。参数优化以相似性密度和个体最优为目标,获得传统支持向量机的最优超参数,改善受超参数影响的算法精度。 以航空发动机涡轮叶盘疲劳寿命数据集为研究案例,证明所提出的DRHOSVM在高维参数下的复杂结构瞬态可靠性分析中的有效性。
1 基于DRHOSVM的复杂结构瞬态可靠性分析
1.1 基于DRHOSVM的复杂结构瞬态可靠性分析流程
在复杂结构瞬态可靠性分析中,由于其功能函数以隐式函数的形式存在,导致采用数值模拟和近似解析法时计算性能低下。为满足工程精度和效率两方面的要求,SVM可在中小样本量的基础上拟合显式功能函数代替原有隐式函数。在此基础上,结合瞬态极值思想,采用SVM将动态输出响应过程转化为极值输出响应过程。然而,SVM在拟合复杂高维非线性问题时存在性能失真问题。DR策略和参数优化的出现为解决这一问题提供了可行的方案。一方面,降维策略在保持高、低维数据空间线性关系不变的同时,将高维数据嵌入低维数据,以避免维数灾难引起的算法效率和精度问题。另一方面,参数优化以相似性密度和个体最优相结合的方式获取SVM的最优超参数,以产生最优模型下的高精度可靠性分析结果。因此,以降维策略为输入参数处理方案,SVM为建模基础,参数优化为最优模型搭建基础,提出DRHOSVM以解决高维变量下的复杂结构瞬态可靠性分析问题。基于DRHOSVM的复杂结构瞬态可靠性分析流程如图1所示。
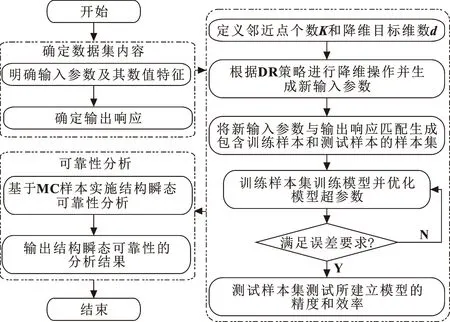
图1 基于DRHOSVM的复杂结构瞬态可靠性分析流程
1.2 DRHOSVM数学模型推导
所提出的DRHOSVM通过在时域[0,T]内建立具有高可靠性和小误差的数据模型,建立复杂结构的高维输入参数与瞬态极值响应之间的关系,以执行可靠性分析。建立DRHOSVM模型的首要任务是获取瞬态极值样本。在获取样本阶段,采用拉丁超立方抽样(Latin Hypercube Sampling,LHS)方法,此方法在保证样本的随机性和相对均匀性的同时,提高了抽样效率。所获得样本一方面作为有限元模拟的输入,生成相应的瞬态极值输出响应;另一方面作为DR的输入,在保证高、低维局部线性关系的基础上,对输入参数进行降维处理,形成与瞬态极值输出响应匹配的低维输入变量,将新输入变量与输出响应结合可生成DRHOSVM的样本集。样本集分为训练样本集和测试样本集,训练样本集被引入HOSVM以训练具有最优超参数的最佳模型,测试样本集用以检验所训练的HOSVM的精度和效率。
所提出的DR策略是一种非线性降维方法,假设D维M个输入样本点X=[x1,…,xM]∈RD×M在规定区域内是线性的,即样本点的数据可由区域内的k个预选点线性表示,远离样本点数据的多余点对局部线性关系没有影响,该策略降低了DR的复杂度和计算量。
初始高维空间的样本点X=[x1,…,xM]∈RD×M和k个预选点的线性关系可通过其均方误差函数表示为
(1)
对于第i个变量xi,其欧几里得距离用于计算整个区域中的所有可能点并升序排列,并选择其中距离最短的k个邻近点xij,j表示变量xi的邻近点的标记数。
为保持高、低维空间的样本点与邻近点的线性关系不变,需在高维空间确定样本点xi的线性重构系数βij,如式(2)所示:
(2)
式中:i、j、l、n和o皆为样本点的标记。
假设降至d维的样本仍保持与D维高维空间同样的线性关系,必须保证其重构系数和邻近点个数不变。因此,只需重构系数和邻近点个数确定后,由xi映射到d维空间中样本坐标uig,即
(3)
式中:uig代表低维映射样本的第i行第g列。
通过DR策略的实施,原输入样本已由D维降至d维。需注意的是,由于线性重构系数的不变性,导致输入样本的维数降低时其包含的信息也保持不变。将新输入样本与极值输出响应进行匹配形成模型样本集,将样本集分为训练样本集和测试样本集。训练样本集用于建立模型,测试样本集用以测试所建立模型的计算性能。模型中建立了输入参数和输出响应之间的回归关系,其关系的准确性影响了复杂结构瞬态可靠性分析的有效性。SVM作为高效的代理模型,应用于回归问题时具有相对较高的精度和效率。因此,选取SVM作为模型的建模基础。
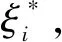
(4)


(5)
式(5)满足卡罗需-库恩-塔克(Karush-Kuhn-Tucker,KKT)条件,因此该原始优化问题可转化为如式(6)所示的对偶问题。
(6)

(7)
将式(7)代入式(6),原始优化问题的对偶形式可变化为
(8)
式中:m代表由DR策略形成的新样本集个体数量;xj表示与xi不同的输入样本。
通过求解式(8),SVM回归函数可得到
(9)
为符合实际工程样本的效率需求和协同DR策略,引入核函数用以代替式(9)中的输入样本内积xiTxj。核函数可表示为
k(xi,xj)=〈φ(xi)φ(xj)〉=φ(xi)Tφ(xj)
(10)

(11)
γ作为SVM回归应用的另一重要超参数,它与高斯RBF的关系为
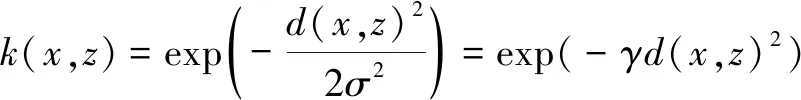
(12)
式中的γ确定了高斯函数的峰值,当γ越大,高斯函数峰值越大分布越密,SVM的支持向量越少;反之,γ越小,高斯函数峰值越小分布越散,支持向量的个数越多。支持向量是构建拟合层的必要要素。当γ的属性反映在SVM回归问题时,其值越大支持向量越少,SVM越容易过拟合。此时,训练时的SVM模型性能优越,但测试性能低下。反之,γ越小的会导致SVM欠拟合。
通过上述分析,超参数C和γ共同影响了SVM回归的泛化和预测能力。为精确地分析复杂结构的瞬态可靠性,有必要通过参数优化设计获得SVM的最优超参数。GA作为启发式寻优算法的代表方法,具有高效率和强鲁棒性,适于SVM超参数寻优的参考算法。由于遗传操作的不足,传统的GA易于局部收敛。因此,为获得SVM超参数的最优值,在传统GA中进行遗传操作的基础上,提出考虑个体相似性密度最低和适应度最优兼具的参数优化算法。个体相似性密度计算如式(13)所示:
(13)
式中:η代表个体适应度;λ表示能容忍的个体适应度相似密度的临界值。
使得相似性密度较小和适应度较大的参数相似性选择两方面兼具的个体形成新种群P(g)″可表示为
(14)
式中:f(ηi) 为第i个个体的适应度值;a和b分别为相似性密度和适应度值的偏向性系数。
新种群P(g)″个体数量只有原有个体数量的一半,因此下一代种群P(g+1)个体数量也同样只产生一半,与新种群P(g)″融合形成g+1代的初始种群以进行下一次迭代计算。当迭代次数满足预设迭代最大值时,参数优化停止,输出具有全局最优值的超参数。
1.3 基于DRHOSVM的复杂结构瞬态可靠性分析
结合DRHOSVM的数学模型,复杂结构的极限状态函数可建立,如式(15)所示:
h(u)=yallow-yDRHOSVM(u)
(15)
式中:yallow和yDRHOSVM(u)分别为复杂结构的瞬态极值允许值和经DRHOSVM推导的预测值。极限状态函数是复杂结构的失效域与安全域的分界线,当h(u)≥0时复杂结构处于安全状态,反之处于失效域。
通过DR策略,原有输入样本的均值和标准差可表示为v=[v1,v2,…,vM]和D=[D1,D2,…,DM]。则极限状态函数的均值和标准差形如
(16)
此时,极限状态函数服从高斯分布,其可靠度可表示为
(17)
2 航空发动机涡轮叶盘的瞬态可靠性分析
涡轮叶盘作为燃气轮机的关键部件,用于承受进入燃烧室的高温高压气流,以维持航空发动机的运行。叶片疲劳是航空发动机发生频率较高的失效形式,也是发动机失效的主要原因。因此,采用所提出的DRHOSVM方法从疲劳寿命角度分析航空发动机涡轮叶盘的瞬态可靠性。
以航空发动机涡轮叶盘(如图2所示)的1/46为研究对象,以其疲劳寿命瞬态极值数据集为案例样本集,其输入参数的均值和标准差见表1。假设输入参数服从正态分布,且相互独立。

表1 输入参数的数值特性

图2 航空发动机涡轮叶盘
为建立涡轮叶盘的DRHOSVM模型,将数据集中包含的146组数据进行DR操作。将原11维的输入变量降至5维,并保持其数据信息不缺失。降维后输入样本的均值和标准差见表2。

表2 降维后输入参数的数值特性
选取前60组数据作为训练样本集,用于建立涡轮叶盘的DRHOSVM模型,后86组数据作为测试样本集验证建立好的DRHOSVM模型的有效性,有效性通过均方误差(Mean Square Error,MSE)和R2说明。MSE评价数据的变化程度,其值越小,说明预测模型描述实验数据的精确度越高。R2是拟合优度,反映模型对样本数据的拟合程度,其值越接近1,拟合效果越好。所建立的DRHOSVM模型应用于测试样本集的预测曲线,如图3所示。
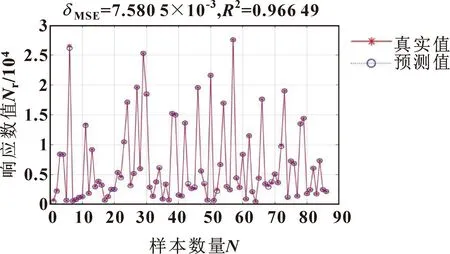
图3 测试样本的真实值与预测值
对于所建立的DRHOSVM,测试样本集的MSE和R2分别为7.580 5×10-3和0.966 49,均处于回归预测的有效域内。
基于复杂结构的瞬态可靠性分析原理,结合所验证的DRHOSVM模型,执行涡轮叶盘的可靠性评估。如图4、5所示,以10 000个MC(Monte Claro,蒙特卡罗)样本为输入,其疲劳寿命分布服从正态分布。通过统计分析,涡轮叶盘的最大允许疲劳寿命为2.200 6×104循环。

图4 分布直方图
输入不同蒙特卡罗样本时涡轮叶盘的可靠度见表3。可以看出:MC模拟次数越多,涡轮叶盘的可靠度越收敛。即越多的蒙特卡罗样本有助于可靠度收敛值的确定。当最大允许疲劳寿命为2.200 6×104循环时,涡轮叶盘的疲劳可靠度为0.997 5。

表3 降维后输入参数的可靠度
3 DRHOSVM算法有效性验证
以建模特性和模拟性能为验证依据,以直接模拟、传统支持向量机、Kriging作为比较对象,验证所提出的DRHOSVM的有效性和适用性。
3.1 建模特性
基于相同计算条件和样本集,通过与传统支持向量机、响应面法的比较验证了DRHOSVM的建模特性。对于航空发动机涡轮叶盘降维数据集,前60个样本用于训练DRHOSVM模型,其余86个样本用于估计开发的DRHOSVM模型的建模误差。针对其余比较算法,在涡轮叶盘疲劳可靠性建模时,采用未降维的原样本集的后86个测试样本,对前60个训练样本建立的相应模型。涡轮叶盘疲劳可靠性的不同建模方法的建模时间和建模误差见表4。
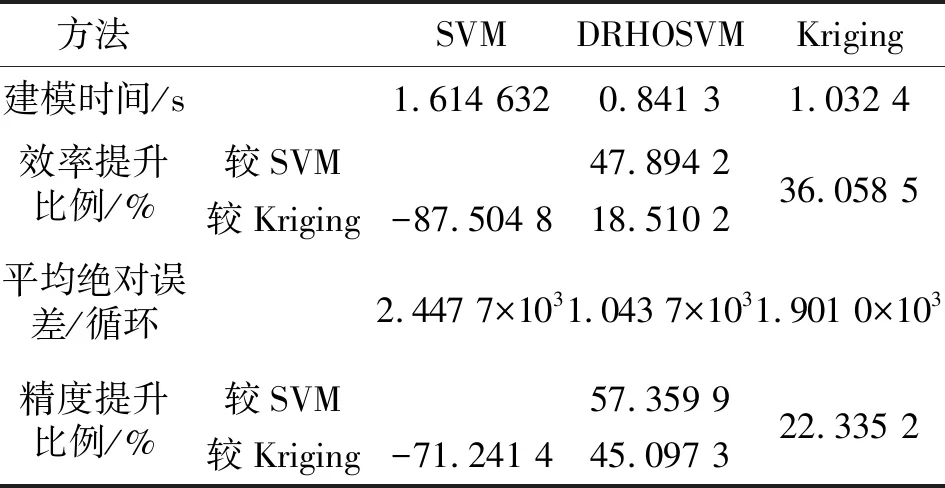
表4 SVM、DRHOSVM及Kriging的建模特性
相对于SVM和Kriging,DRHOSVM在建模效率和建模误差上都表现最优,证明了DRHOSVM建模速度和建模精度的优越性。DRHOSVM在建模效率方面,较SVM提升了47.894 2%,较Kriging提升了18.510 2%。DRHOSVM在建模精度方面,较SVM提升了57.359 9%,较Kriging提升了45.097 3%。出色的建模特性不仅来自于DRHOSVM对高维数据进行了保留数据信息的降维处理,并且通过参数优化算法建立了最优模型。
3.2 模拟性能
在仿真性能方面,以直接模拟、SVM和Kriging作为比较方法,验证应用于复杂结构瞬态可靠性分析的DRHOSVM的有效性。对于不同的MC样本(5×102、103、3×103、8×103和104),以直接模拟方法作为验证中的评价指标,SVM、Kriging和所提出的DRHOSVM在模拟效率、可靠性水平和模拟精度方面的模拟性能,见表5、6。考虑到难以承受的计算负担,104个蒙特卡罗样本不应用于直接模拟方法。

表5 不同蒙特卡罗样本数量各方法的模拟时间
从表5可看出:DRHOSVM应用于5组不同的蒙特卡罗样本时的模拟效率明显高于其余方法。当蒙特卡罗样本量为104时,DRHOSVM的模拟时间为0.024 0 s,SVM次之。DRHOSVM的高模拟效率是由于DR策略的实施将高维数据降至低维空间,使得计算难度和复杂度减小。
从表6可看出:DRHOSVM在可靠度和模拟精度上皆为4种方法的最优者。DRHOSVM的可靠度在MC样本个数为8×103时收敛到稳定值0.997 5。以直接模拟方法结果作为比较依据,应用于涡轮叶盘疲劳可靠性分析的DRHOSVM的模拟精度达到99.989 9%,高于SVM和Kriging。原因为所提出的DRHOSVM采用了相似度密度和个体最优兼具的参数优化方法,以最优超参数建立了应用模型。因此,DRHOSVM具有较好的模拟特性。
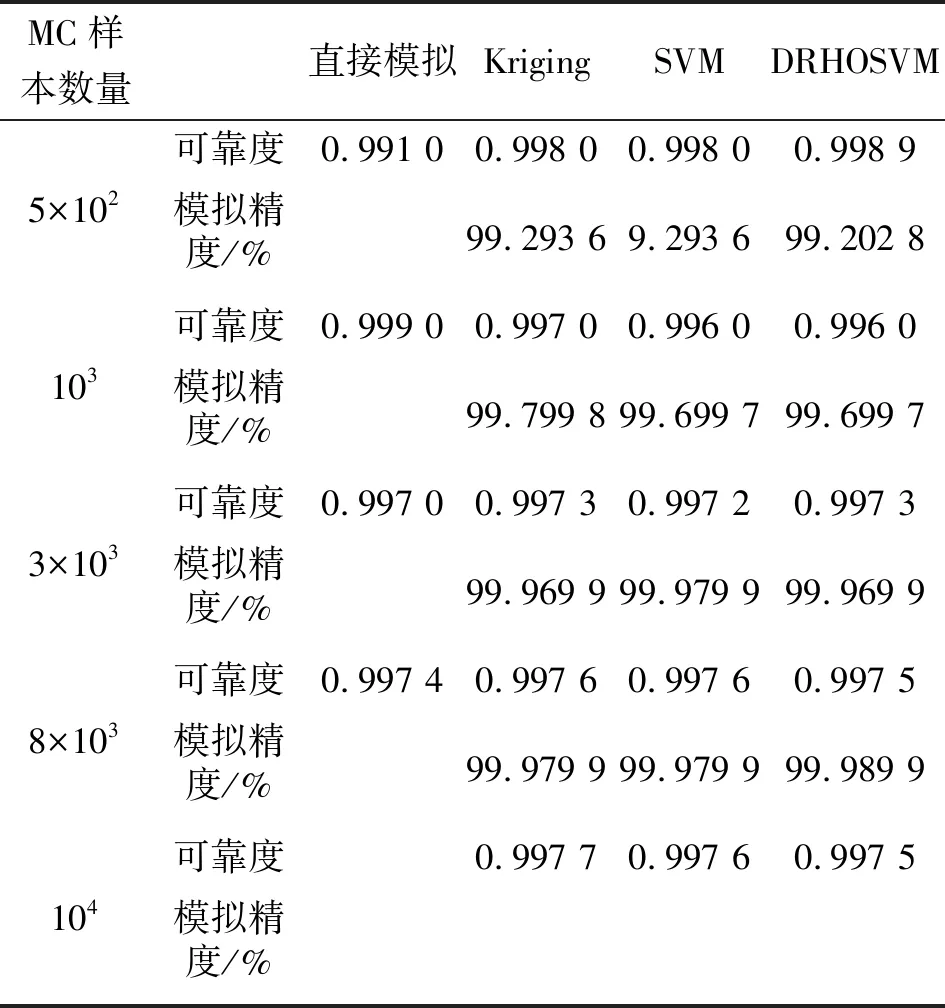
表6 不同蒙特卡罗样本各方法模拟的可靠性水平和模拟精度
4 结论
通过引入DR策略和参数优化算法,提出DRHOSVM以提高传统支持向量机SVM在复杂结构瞬态可靠性分析中的性能。在训练和测试过程中,以航空发动机涡轮叶盘数据集作为对象。为检验所提出的DRHOSVM的性能,在建模特性和模拟特性方面与直接模拟、Kriging和SVM进行对比,可以得出:
(1)4种预测方法的误差均在工程实际应用的接受的范围内,与Kriging和SVM相比,DRHOSVM模型具有较高预测精度,所建立模型的平均绝对误差为1.043 7×103循环。
(2)与其他方法相比,所提出的DRHOSVM在建模效率方面具有优势。DRHOSVM所消耗的建模时间为0.841 3 s,低于Kriging模型和传统的SVM模型。此外,DRHOSVM在模拟速度与建模时间方面同样表现优秀,在104个蒙特卡罗样本中,DRHOSVM以0.024 0 s完成模拟,这表明DRHOSVM在建模和仿真过程中兼具高效率。
所提出的DRHOSVM为复杂结构瞬态可靠性分析提出了可行的新思路,对于高维参数复杂结构的优化设计具有重要意义。
