径向磁液轴承的转子散热规律研究
2023-12-20陈丽文赵建华赵计胜吴晓晨崔冰艳杨中原
陈丽文,赵建华,赵计胜,吴晓晨,崔冰艳,杨中原
(1.华北理工大学机械工程学院,河北唐山 063210;2.燕山大学机械工程学院,河北秦皇岛 066000;3.中车唐山机车车辆有限公司,河北唐山 063000;4.中煤科工集团唐山研究院有限公司,河北唐山 063000)
0 前言
磁液轴承是一种新型轴承,应用于航空航天、船舶舰艇等重大装备领域。近年来研究人员不断探索,研发了一种带小孔节流器的超导磁力与静压力复合推力轴承,分析了复合轴承静动性能[1],对火箭发动机高温超导与液膜复合轴承作了静力学特性和动力学特性分析[2-3],设计一种全新的复合式水润滑轴承,增强船舶轴系运行稳定性[4]。本文作者研究的磁液轴承由电磁支承系统和静压支承系统组成,可以实现主动控制。轴承主要有铜损及铁损两个热源,由于线圈通直流电且定子固定不动,因此定子内不存在涡流损耗,而转子在运行时内部的磁场方向不断改变产生感应电动势,从而产生涡流损耗。转子的铁损会导致轴承转子部位温度升高,进而产生热变形,造成定转子之间的间隙变小,从而影响轴承承载性能,甚至会造成定转子之间碰摩,严重影响轴承使用寿命[5-6]。
1 有限元分析模型
本文作者利用Maxwell仿真软件仿真求解轴承转子产生的涡流损耗,并通过改变运行参数,探索转子散热规律的变化,为轴承稳定性奠定理论基础。
1.1 Maxwell二维模型建立
对磁液轴承的涡流损耗建立仿真模型,利用Ansoft Maxwell软件对其进行仿真求解。在Maxwell中,二维模型求解精度更高且节省计算内存及计算时间。将轴承简化为二维模型对其进行涡流损耗仿真计算[7-9],仿真模型如图1所示。

图1 磁液轴承涡流损耗仿真模型
为避免计算过程中软件运行产生错误,对模型进行了简化处理,忽略线圈槽的圆角及转子上的螺纹。
1.2 有限元模型尺寸参数
在Maxwell中按表1、表2设置轴承的材料属性和初始设计参数。磁液轴承的有限元模型尺寸参数如图2所示,其中转子的直径为36 mm,为了增加导磁性,减少涡流损耗,在转子外镶嵌导磁套,外径为60 mm。

表1 材料属性
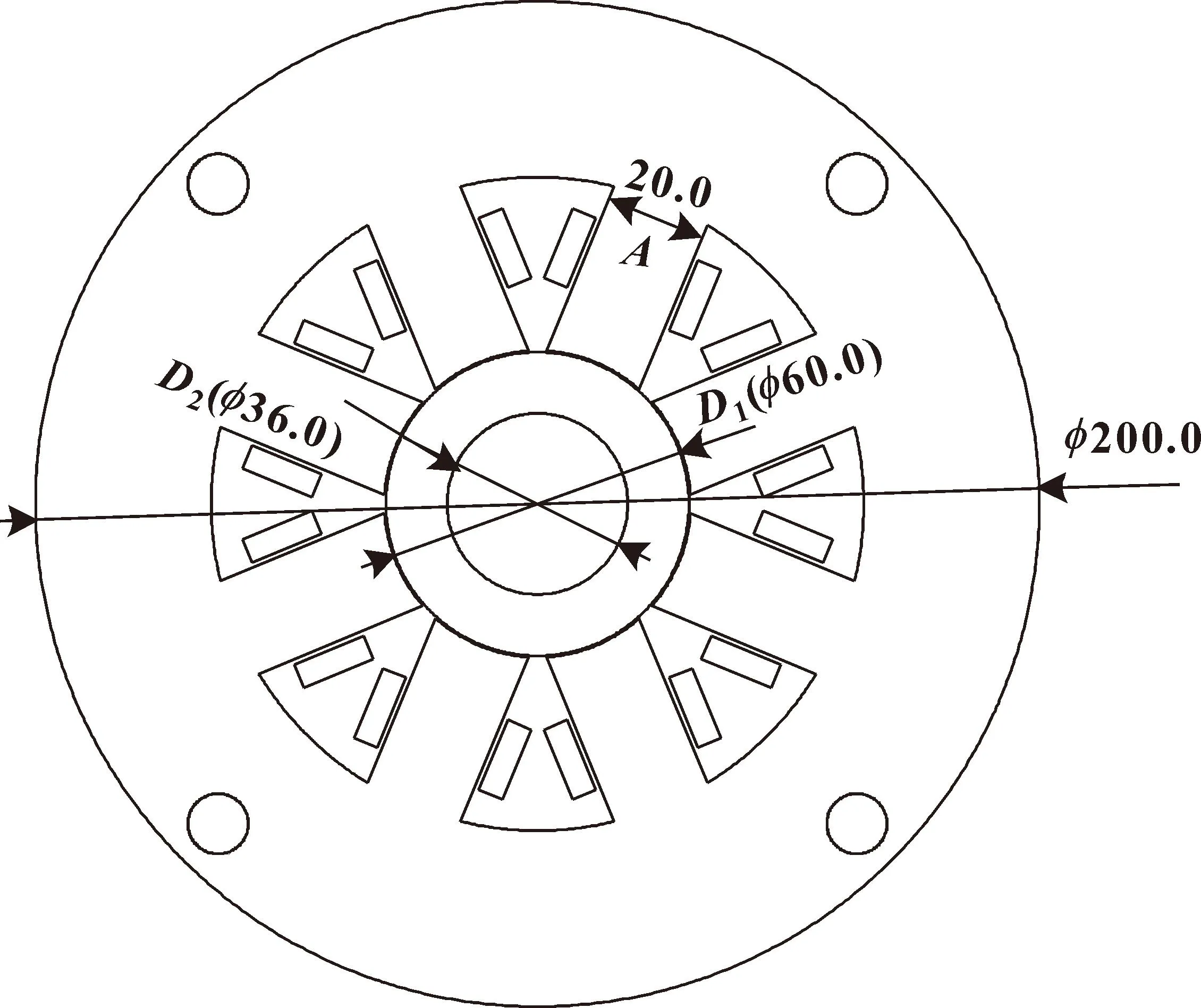
图2 有限元仿真模型尺寸示意
利用耦合传热方式求解径向轴承、线圈、流体三者之间的热交换,以保证三者之间的耦合面热量连续。
(1)转子两侧端面与外界的换热系数
转子旋转时其两侧端面与空气相对运动,其换热系数可按下式计算[10]:
式中:h1为转子两侧端面与外界的换热系数,W/(m2·℃);u为旋转轴表面线速度,m/s;r为旋转半径长度,m;n为转子转速,r/min。
当转速n=2 000 r/min时,转子两侧端面与外界的换热系数h1=25.12 W/(m2·℃)
(2)耦合传热面之间的换热系数
由于线圈产生热量与流体冷却线圈是同时发生、同时进行的,因此两者之间的传热率不能预先设置。在Fluent中将流体-线圈、线圈-定子磁极、转子-流体之间的传热面设置为耦合传热面,以保证三者之间的热流密度连续。图3所示为以上3个传热面示意图。

图3 磁液轴承传热面示意
2 初始模型仿真结果
2.1 磁液轴承磁场分析
采用瞬态磁场模型仿真计算,时间步长取0.02 s,总的计算时长取1 s进行仿真。计算后得到轴承的磁场仿真结果如图4所示。
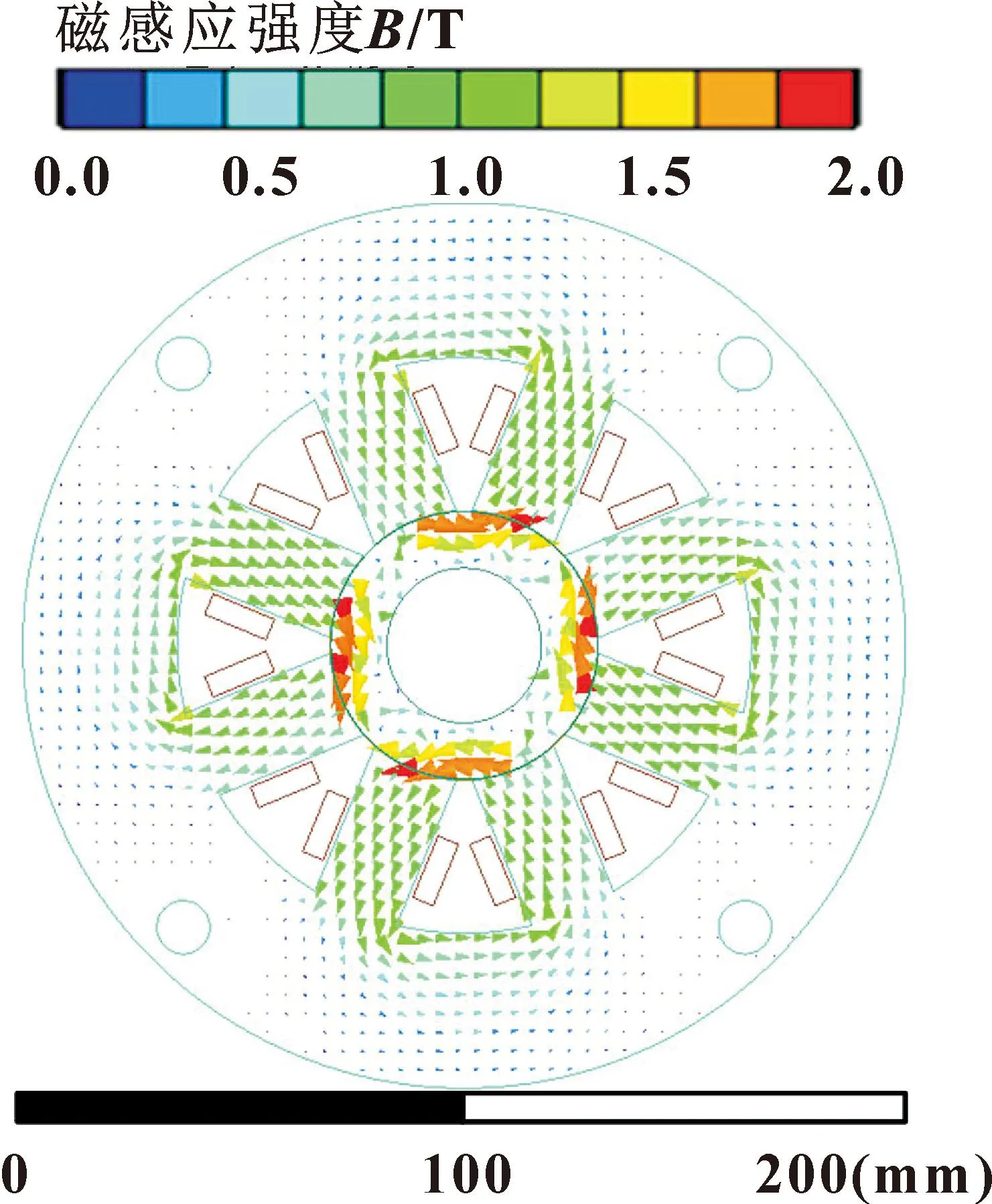
图4 磁感应强度分布
图4所示为轴承磁感应强度分布,磁感应强度在轴承的导磁套处较大。这是由于导磁套厚度相对于磁极略窄,磁场密度集中于导磁套内。由图4可知,轴承产生的磁感应强度最高为2.0 T。
图5所示为轴承在2 000 r/min时的涡流损耗,可知:0.15 s后涡流损耗达到稳定,最后稳定值为26.2 W。
2.2 转子温度场分析
初始温度设为20 ℃,根据耦合传热求解轴承转子温度场,结果如图6所示。

图6 轴承转子温度分布云图
由图6可知:转子温度场呈对称分布,中心部位温度较低,这是由于出油口通入的均为恒温油液,不断对轴承转子进行冷却,随着油液流出油口流动速度变缓,油液的冷却速度下降,转子温度逐渐增高。轴承转子的平均温度为25.94 ℃。
2.3 转子热变形分析
将转子温度导入至Static Structural模块求解转子的应变,结果如图7所示。可知:转子的热变形呈均匀对称分布,随后由内向外逐渐增大,在磁极两端处热变形最大,达到1.83 μm。

图7 导磁套应变云图
3 参数变化对导磁套散热规律的影响
导磁套热变形产生的根本原因一是导磁套内部产生的涡流损耗发生了变化,二是导磁套的散热规律发生了改变。导磁套涡流损耗的耗散途径有3种方式[11],如图8所示。
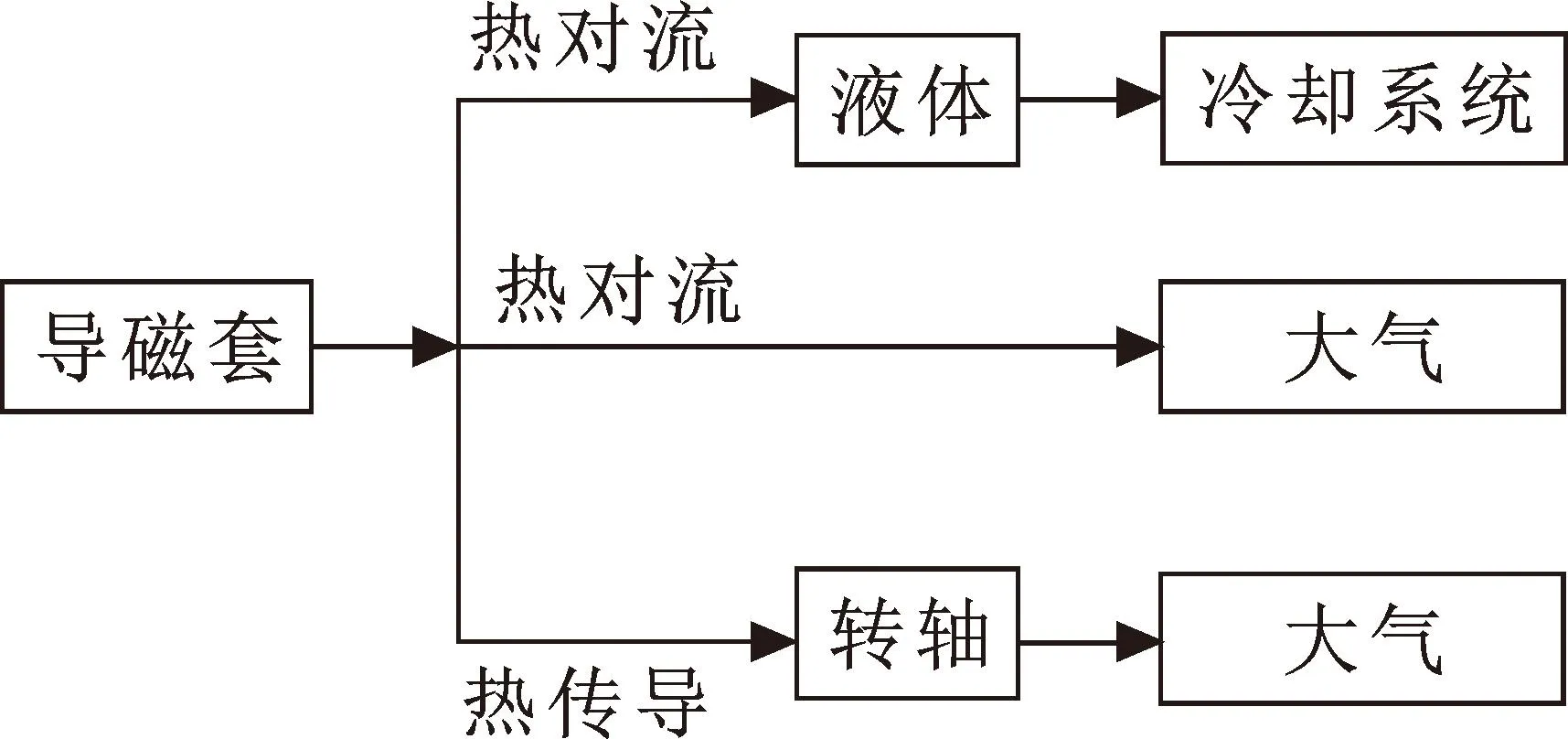
图8 导磁套涡流损耗耗散途径
由图8可知:轴承导磁套产生的热损耗一部分由液体及大气冷却,另一部由热对流到大气,还有部分经热传导传递至转轴,再由转轴散发至大气中。文中通过提取导磁套-液体、导磁套-大气、导磁套-转轴以及转轴-大气之间的传热率来分析运行参数变化对导磁套散热规律的影响。
3.1 输入电流对导磁套散热规律的影响
输入电流直接影响导磁套内产生的涡流损耗的大小,涡流损耗的变化造成了导磁套温升提高,使导磁套与转子、流体及大气之间的温差加大,进而影响导磁套的散热规律。提取各耦合面之间的传热率,研究导磁套散热效率随输入电流的变化规律,结果如表3所示。表中η1=P1/Pw×100%代表导磁套-流体传热率与涡流损耗的比值,η2=P2/Pw×100%代表导磁套-大气传热率与涡流损耗的比值,η3=P3/Pw×100%代表导磁套-转轴传热率与涡流损耗的比值。由表3可知:随着输入电流的增大,轴承涡流损耗增加,与此同时导磁套与流体、大气、转轴之间的传热率也随之增加;η1、η2、η3随着输入电流的增加无明显变化,可知输入电流对轴承的散热规律无明显影响。

表3 传热率随输入电流的变化
3.2 转速对导磁套散热规律的影响
转子与导磁套同步转动,随着转速的增加转子端面与空气之间的相对速度增加,转子两侧与空气之间的换热系数会随着转速增加,导致导磁套-大气传热率增加,进而影响导磁套的散热规律,提取耦合面之间的散热效率,结果如表4所示。

表4 传热率随转速的变化
由表4可知:随着转速的增大,轴承涡流损耗增加,与此同时导磁套与流体、大气、转轴之间的传热率也随之增加。导磁套两侧与大气之间的传热率增加,进而P2及η2随转速增加。随着转速由2 000 r/min增加至6 000 r/min,η1由95.18%减小至89.83%,减小了5.35%;η2由3.18%增加至6.74%,增加了3.56%;η3由1.64%增加至3.43%,增加了1.79%。
3.3 进油流量对导磁套散热规律的影响
磁液轴承流量大小基本不影响导磁套涡流损耗的大小,但会影响轴承内部流场流动速率,流速增加必然会加快轴承的冷却,进而影响导磁套的散热规律。提取各耦合面之间的传热率,导磁套散热效率随进油流量的变化规律如表5所示。

表5 传热率随进油流量的变化
由表5可知:磁液轴承随着进油流量的增大,轴承内部流速增快,进而导致了P1及η1增大,P2以及P3降低,随着进油流量由0.02 L/min增加至0.06 L/min,η1由95.18%增加至96.90%,增加了1.72%;η2由3.18%减小至2.07%,减小了1.11%;η3由1.64%减小至1.03%,减小了0.61%。
4 磁液轴承系统油温测定
磁液轴承试验台主要由磁液轴承系统、动态信号测试分析系统两部分组成。磁液轴承系统稳定运行时轴承进出油口温度将产生变化,通过温度传感器采集出油口温度,得到油温变化规律。磁液轴承系统由供油系统和轴承系统两部分组成,分别如图9和图10所示。供油系统向轴承主体输入带有一定压力的液压油,轴承主体通过液压油的静压效应实现转轴的稳定悬浮。

图9 磁液轴承供油系统

图10 磁液轴承系统
因为油箱体积较大所以进油口温度可以视为恒定且为室温,利用出油口的温度传感器测量不同输入电流下出油口温度,然后减去油箱油温,进而得到不同输入电流下进出油口的温差。试验与仿真计算所得进出油口温差曲线图如图11所示。
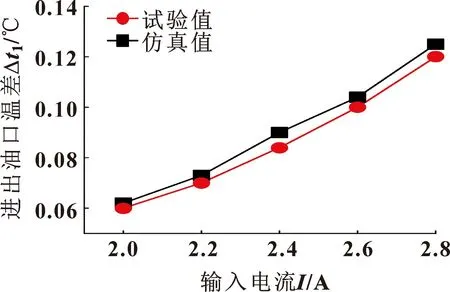
图11 不同电流下进出油口温差仿真值与实测值
由图11可知:仿真时轴承进出油口温差随输入电流的增加呈线性增长趋势,随着电流由2.0 A增加至2.8 A,进出油口温差由0.06 ℃线性增加至0.12 ℃;实际测量值与仿真结果存在一定偏差,最大误差为6.7%,进出口温差与仿真值趋势一致。
利用出油口的温度传感器测量不同转速下出油口温度然后减去油箱油温,进而得到不同转速下进出油口的温差。试验与仿真计算所得进出油口温差曲线如图12所示。

图12 不同转速下进出油口温差仿真值与实测值
由图12可知:仿真时轴承进出油口温差随转速的增加基本保持不变,随着转速由40 r/min增加至200 r/min,进出油口温差始终保持0.06 ℃;而试验时轴承进出油口温差由0.064 ℃增加至0.07 ℃,温差随着转速的增加逐渐变大但变化不明显。这是由于仿真时在理论情况下设定进油温度是恒定的,未考虑油泵电机的发热损耗,而实际试验时油泵电机发热会导致油液温度升高。试验测量的进出口温差趋势与仿真基本值一致,最大误差为14.3%。
5 结论
(1)求解了磁液径向轴承的涡流损耗模型,初始参数下,轴承产生的磁感应强度最高为2.0 T,涡流损耗最后稳定值为26.2 W,转子的平均温度为25.94 ℃,转子的热变形达到1.83 μm。
(2)基于多场耦合作用分析了参数变化对导磁套涡流损耗及散热规律的影响。结果表明:随着输入电流、转速的增加,导磁套的涡流损耗均为增高趋势,输入电流的变化对轴承的散热规律无明显影响。
(3)随着输入电流的增加,进出口温差实验值与仿真值均线性增加;随着转速增 大,轴承进出油口温差基本保持不变,是由于仿真时设定进油温度恒定,试验时油泵电机发热会导致油液温度升高。试验值与仿真值误差在可接受范围内,验证了仿真结果的可靠性。
