基于数字孪生的液压支架姿态监测
2023-12-20杨崇浩白国长
杨崇浩,白国长
(郑州大学机械与动力工程学院,河南郑州 450001)
0 前言
煤炭作为能源结构的重要组成部分,其开采过程环境恶劣、危险性高,因此迫切需要实现智能化开采[1]。液压支架作为综采工作面的支护设备,为整个综采工作面的安全可靠运行提供了重要保障,液压支架的姿态对其承载能力以及结构的稳定性具有很大的影响,因此对液压支架姿态的可靠监测是实现煤炭智能化开采的前提[2]。
液压支架的姿态主要包括其顶梁和底座的姿态。近年来,国内外许多学者对液压支架姿态的监测方法进行了相关研究。陈冬方、李首滨[3]引入4个双轴倾角传感器,实现对液压支架顶梁高度的监测。廉自生等[4]利用Zigbee技术构建液压支架姿态监测网络,实现液压支架姿态的全面感知。胡相捧、刘新华[5]建立液压支架姿态与驱动千斤顶的一一映射关系,实现初撑阶段液压支架顶梁和底座姿态的监测。任怀伟等[6]利用深度视觉技术实现液压支架姿态的精准感知与动态监测。
数字孪生作为一种将现实空间的物体精确地映射到虚拟空间的技术,自2003年由GRIVES教授提出以来逐渐得到了广泛的应用,尤其在状态监测方面[7]。DAN等[8]通过构建基于机器视觉融合的数字孪生模型实现了桥梁交通载荷的监测。XIE等[9]通过构建基于物理与虚拟数据融合的数字孪生模型实现了刀具状态的监测。WANG等[10]构建基于数据融合和Bi-LSTM网络的数字孪生模型,实现了光通信过程的状态监测和故障诊断。LIU等[11]构建基于虚实融合和LSTM网络的数字孪生模型,实现了涡扇发动机的状态监测。ZHOU等[12]构建基于传感器数据和OPC UA信息模型的数字孪生模型,实现了港口起重机的状态监测。数字孪生模型的构建方法目前尚不统一,其中TAO等[13]提出的由物理实体、虚拟实体、数据、连接和服务组成的五维模型应用较为广泛。
结合数字孪生技术在其他领域的应用情况,发现现有的基于传感器数据和图像的液压支架姿态监测方法主要存在以下问题:(1)传感器数据折线图和监控图像对姿态的表示不够直观;(2)传感器及监控数量有限,很难反映支架的整体姿态;(3)受地下环境和数据传输条件的影响,监测的图像质量差、可靠性不强。本文作者基于信息融合技术,提出一种用于液压支架姿态监测的五维数字孪生模型的构建方法,以实现液压支架姿态的全面监测和异常预警,具体开发框架如图1所示。

图1 液压支架数字孪生模型开发框架
1 液压支架姿态监测的数据驱动模型
1.1 液压支架姿态的表示与解算
液压支架的姿态数据通过其顶梁和底座所安装的惯性测量单元(Inertial Measurement Unit,IMU)进行采集,在惯性测量中,为了描述质点的位置以及运动情况,需要选择相应的坐标系。液压支架的载体坐标系O-xyz如图2所示,图中位置1处为IMU。

图2 液压支架的载体坐标系
文中以液压支架的体坐标系O-xyz为载体坐标系,以东北天坐标系O-XYZ为参考坐标系。初始状态时,两坐标系重合,当液压支架姿态变化后,载体坐标系可以理解为由参考坐标系依次绕z、x、y轴内旋得到。坐标系之间的转换关系如图3所示。
在惯性测量中,为了更好地表示角度的变化,并考虑到计算过程对硬件资源的占用,通常采用四元数法来进行姿态的求解。四元数定义为
(1)
式中:q0、q1、q2、q3为实数;i、j、k为与载体坐标系基相一致的标准正交基;u和φ分别为载体坐标系相对参考坐标系旋转轴的单位矢量和旋转角度。
由四元数的转动定理及四元数的运算法则可得参考坐标系到载体坐标系的坐标转换关系的四元数表达为
(2)
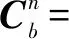
可得横滚角γ、俯仰角θ与四元数的关系为
(3)
1.2 液压支架姿态的测量算法
在使用IMU采集液压支架姿态数据时,由于陀螺仪存在零偏及环境变化会引起随机误差,且这些误差会随积分逐渐积累,导致所测长期数据的精度降低;而加速度计容易受到振动和非重力加速度的影响,从而导致所测短期数据的精度降低。文中以加速度计的数据为观测量,以陀螺仪的数据为预测量,通过卡尔曼滤波融合2组数据以得到更精确的液压支架姿态。
液压支架姿态的惯性测量系统可近似为线性系统,其状态和观测方程为
(4)
式中:xk为k时刻系统的状态向量;yk为k时刻系统的观测向量;A为状态转移矩阵;H为观测矩阵;ωk-1为系统噪声;vk为观测噪声。
在液压支架姿态的实际测量中,建立系统的状态更新方程:
(5)
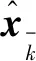
系统的量测更新方程为
(6)

1.3 液压支架姿态的数据驱动模型
在液压支架姿态测量系统中,通过卡尔曼滤波处理后的姿态数据可以建立平稳时间序列对液压支架的姿态进行描述,考虑到序列具有较强的周期性,液压支架姿态监测的数据驱动模型可以选择自回归滑动平均模型进行描述,形式如下:
xk=ψ1xk-1+ψ2xk-2+…ψpxk-p+εk+
θ1εk-1+θ2εk-2+…+θqεk-q
(7)
式中:xk为k时刻液压支架的姿态值;ψ1、ψ2、ψp为自回归模型的参数;{εk}为高斯白噪声;θ1、θ2、θq为滑动平均模型的参数。
由于递推最小二乘法方法具有计算量小、收敛速度快等优点。构建模型参数递推状态方程,通过递推最小二乘法及数据更新实现其在线更新。将式(7)转换为最小二乘形式:
(8)

模型参数的递推最小二乘法计算公式为
(9)
2 液压支架姿态监测的物理模型
液压支架数据驱动模型中的数据来源为相应的传感器数据,然而安装在液压支架上的传感器类型和数量有限,不能准确全面地反映液压支架的工作状态。液压支架的物理模型可根据液压支架的工作原理计算传感器的未测量参数,以弥补测量参数的不足,从而在有限传感器的前提下实现对液压支架姿态的全面监测。液压支架的物理模型主要包括其运动学模型、环境数据以及其物理实体的同步控制信号,通过上述模型的仿真得到液压支架物理模型的姿态数据。
2.1 液压支架的运动学模型
液压支架的运动学模型主要用于模拟它在不同工况下各主要结构件的位置变化,在获取传感器数据的前提下实现对液压支架姿态变化的全面分析。液压支架姿态监测的二维运动学模型如图4所示,以底座端点O为坐标原点,以水平方向为x轴,以竖直方向为y轴。

图4 液压支架的运动学模型
根据液压支架的二维运动学模型及闭环矢量原理可构建液压支架运动学方程为
-L1+L4cosθ3+H5sinθ4=L3cosθ1+H4sinθ4+
L5cosθ4
(10)
H2+L4sinθ3-H5cosθ4=H1+L3sinθ1-H4cosθ4+L5sinθ4
(11)
-L2+L9cosθ2-H9sinθ5+(L10+L11)cosθ5=
L4cosθ3+H5sinθ4+(L6+L7)cosθ4-H7sinθ5
(12)
H3+L9sinθ2+H9cosθ5+(L10+L11)sinθ5=
L4sinθ3-H5cosθ4+(L6+L7)sinθ4+H7cosθ5
(13)
(14)
图4及公式(10)—(14)各参数的物理意义如表1所示。

表1 液压支架运动学模型参数的物理意义
2.2 液压支架的环境数据与控制信号同步
液压支架的控制信号同步在文中主要是指同步立柱和平衡缸控制信号的数据,环境数据同步主要是指综采工作面底板和顶板的起伏形态,以实现液压支架姿态的解算和全面监测。在液压支架设计尺寸已知的前提下,式(10)—(14)构成的方程组有7个未知数,分别为:θ1、θ2、θ3、θ4、θ5、L8和L9。当θ6的值变化时,θ1、θ2、θ3、θ4、θ5的计算结果要抵消相应的值。L8、L9可由液压支架立柱和平衡缸的同步控制信号得到。因此剩余的5个参数θ1、θ2、θ3、θ4、θ5可由式(10)—(14)联立求得。
3 液压支架姿态监测的数字孪生模型
数据驱动模型随着液压支架的工作状态变化而更新,对液压支架姿态变化具有良好的适应性。但是数据驱动模型受数据的影响较大,对于历史数据中没有液压支架姿态的,数据驱动模型由当前数据给出导致计算结果不合理。物理模型根据液压支架的工作原理、环境数据以及同步控制信号得到液压支架的姿态数据及其他传感器未测量到的液压支架姿态的理论数据,该数据准确性和适应性较差。因此文中采用长短期记忆(Long Short-Term Memory,LSTM)网络对数据驱动模型和物理模型的数据进行处理,从而得到更为准确的液压支架姿态信息。
在LSTM网络中,通过大量学习数据驱动模型和物理模型来估计液压支架的姿态信息作为数字孪生模型,LSTM网络结构如图5所示。
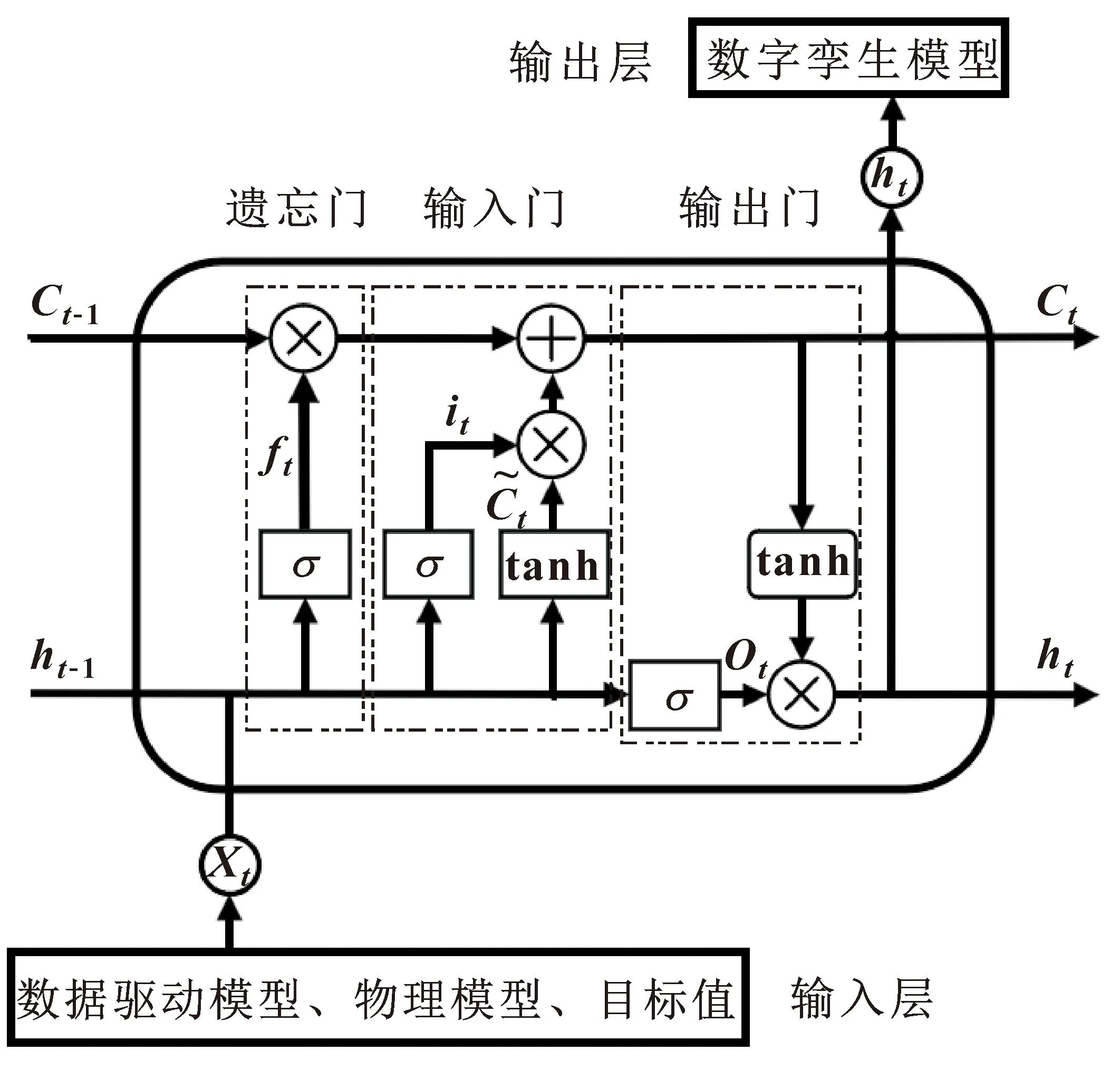
图5 LSTM网络结构
LSTM网络设计了3个门,分别为遗忘门、输入门和输出门,用于控制LSTM网络单元的状态,其中:遗忘门决定Ct-1的哪些特征被计算Ct;输入门决定加入多少新的信息;输出门决定输出什么值。在LSTM网络单元中,门σ可以认为是一个sigmoid函数
σ(x)=1/(1+e-x)
(15)
遗忘门读取ht-1和xt后输出一个在[0,1]内的值与Ct-1中的数值相乘:
ft=σ(Wf·[ht-1,xt]+bf)
(16)
式中:σ表示sigmoid函数;Wf为遗忘门的权重矩阵;ht-1为上一个LSTM单元的输出;xt为当前单元的输入;bf为遗忘门的偏置项。

it=σ(Wi·[ht-1,xt]+bi)
(17)
(18)
式中:tanh是状态激活函数。
输出门首先通过门σ决定将哪些信息输出,然后将单元状态通过tanh层处理,最后结合2个部分确定单元的输出:
ot=σ(Wo[ht-1,xt]+bo)
(19)
ht=ot⊙tanh(Ct)
(20)
由图5可知,LSTM网络输入层包括三部分:数据驱动模型、物理模型的数据和以高精度倾角传感器数据为参照的目标值。输出层作为数字孪生模型的数据来源。LSTM网络训练的目的是优化输入数据的权重使输出数据更好地拟合目标值,其中,优化器函数是快速收敛的Adam梯度下降算法,超参数范围通过仿真确定。
4 实验与结果分析
4.1 实验系统的建立
搭建液压支架姿态监测系统,主要由液压支架、乳化液泵站、液压支架控制器、上位机、GY-521型IMU以及高精度倾角传感器组成。
4.2 评价指标
在误差值的各评价指标中,均方根误差(Root-Mean-Square Error,RMSE)对异常值更敏感,因此文中以均方根误差为液压支架姿态估计的评价指标,用于衡量估计值与目标值之间的偏差,用公式表示为
(21)
式中:ypi为液压支架姿态的估计值;yi为液压支架姿态的目标值。
4.3 实验结果
以高精度倾角传感器的值为目标值,对比并分析液压支架在“升架”过程中IMU数据、数据驱动模型、物理模型和数字孪生模型数据的有效性,如图6—9所示。

图6 IMU的卡尔曼滤波
图6所示为液压支架“升架”过程中安装在顶梁和底座的IMU数据经过卡尔曼滤波的处理结果。可得:卡尔曼滤波处理后的IMU姿态数据中,顶梁俯仰角与目标值的RMSE最大,为0.245 1°;底座横滚角与目标值的RMSE最小,为0.028 4°,且2组数据整体拟合度较好,可以满足监测系统的要求。
图7所示为液压支架姿态监测数据驱动模型的数据处理结果。可知:液压支架姿态监测数据驱动模型的数据中,顶梁俯仰角与目标值的RMSE最大,为0.281 4°;底座横滚角与目标值的RMSE最小,为0.026 5°,且2组数据整体拟合度较好,可以满足监测系统的要求。

图7 数据驱动模型的支架姿态监测曲线
图8所示为液压支架姿态监测物理模型的数据处理结果。可知:液压支架姿态监测数据驱动模型的数据中,顶梁俯仰角与目标值的RMSE最大,为0.847 2°;底座横滚角与目标值的RMSE最小,为0.011 4°,其中顶梁姿态的2组数据拟合度较差,不符合检测系统的要求。
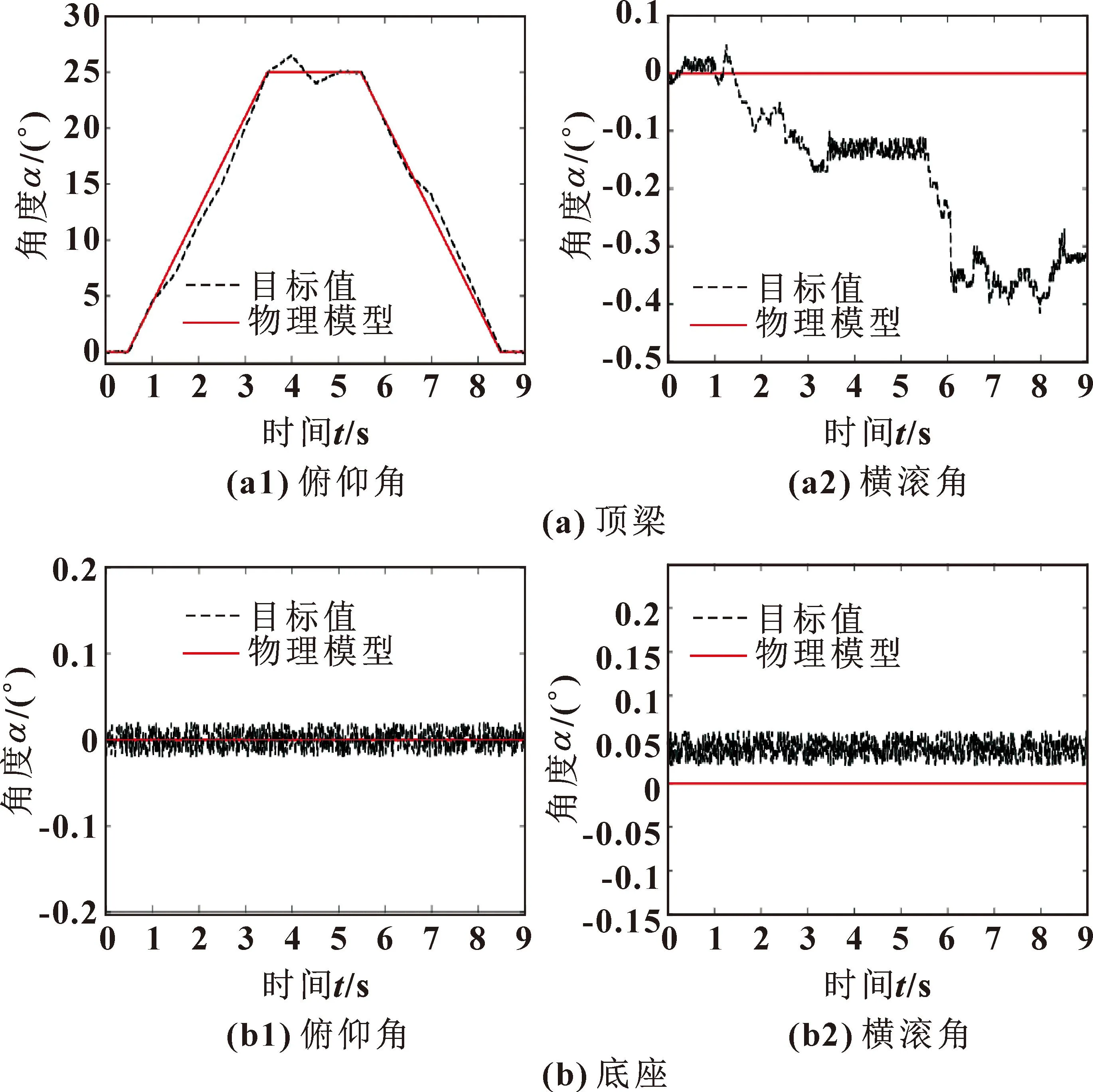
图8 物理模型的支架姿态监测曲线
图9所示为液压支架姿态监测数字孪生模型的数据处理结果。可知:液压支架姿态监测数据驱动模型的数据中,顶梁俯仰角与目标值的RMSE最大,为0.245 4°;底座俯仰角与目标值的RMSE最小,为0.019 1°,相较于支架姿态监测的数据驱动模型和物理模型监测性能均有不同程度的提升,且2组数据整体的拟合度较好,提高了支架的姿态监测性能。
以顶梁俯仰角为例,图10所示为当前液压支架姿态出现历史数据中没有的液压支架异常姿态时各模型的支架姿态监测曲线。可知:在出现历史数据中没有的异常数据时,数据驱动模型与目标值的RMSE为0.510 2°;物理模型与目标值的RMSE为0.507 7°,在7.8 s出现异常姿态后数据驱动模型的数据与目标值拟合度较差,物理模型的数据与目标值整体拟合度较差,对支架的监测能力较弱。数字孪生模型与目标值的RMSE为0.269 5°,且整体拟合度较好,可以满足监测系统的要求,提高了支架姿态监测结果的可靠性。
5 结论
文中针对现有液压支架姿态监测所存在的问题,以液压支架“升架”过程为例,通过信息融合、数据驱动等方法,构建了用于液压支架姿态监测的数字孪生模型,并通过实验验证了该方法的有效性。该方法可以实现液压支架姿态的全面、可靠监测,并可用于姿态的异常预警;同时为数字孪生模型的构建以及液压支架的姿态监测提供参考。
