软铁磁矩形薄板非线性运动的扩展伽辽金法近似分析

王 奥, 陈 东, 曹立染

安徽建筑大学 土木工程学院, 安徽 合肥 230601

随着现代高新技术的推进与发展,以磁、电等材料作为结构的装置的使用愈加频繁。矩形薄板广泛应用于道路及桥梁建设、机械产业、船舶工程、航空航天等领域,当系统受到外界干扰时,板会产生非线性运动行为。近几十年,许多学者对板的振动问题进行了大量的研究,得到了很多有意义的结论。CHEN等[1-2]讨论了四面体磁芯谐波激发板在热载荷影响下的稳定性和非线性响应。MOON等[3]利用动力分岔分支理论对磁弹性非线性运动方程进行了研究。LU等[4]分析了磁性梁式板在周期时变磁场和轴向周期激励共同作用下的动力分岔问题。PAO和YEH[5]引入麦克斯韦应力张量,建立了磁弹性力学模型。胡宇达等[6-7]推导了横向磁场中磁弹性矩形薄板的非线性运动微分方程。李晶等[8]针对横向磁场中的条形板和矩形板,分析系统在内共振非线性动力学问题。SH等[9]基于一阶剪切变形(FSDT)理论、冯·卡曼的非线性应变-位移关系以及修正的定律,研究了多孔功能梯度磁电弹性(PFG-MEE)板的几何非线性自由振动和瞬态响应。

伽辽金(Galerkin)方法是弹性构件和结构固有频率近似计算的常用方法,尤其是在没有解析解或振动方程难以修改和求解的情况下[10-13]。经大量研究表明,伽辽金方法的使用通常可将问题转变为涉及从平衡方程或运动方程计算问题物理域上的函数加权积分,并可将其与一些新技术结合使用,以便更好地解决工程振动中的非线性问题,同时它也是当今应用广泛的有限元方法的基础。关于伽辽金方法的应用有很多,但其本质是通过减小解域上误差的加权积分,将近似解的误差最小化[14-15]。

本文研究考虑在磁化及涡电流条件下产生磁场的激励,通过采用扩展伽辽金方法对软铁磁矩形薄板进行近似分析,得到其非线性运动频率的近似解。

1 扩展的伽辽金方法

对于非线性微分方程

(1)

在不失一般性的情况下,设近似解为

q=∑Ancosnωt。

(2)

将时间视为自变量,在一个运动周期内使用伽辽金方法[14-16]:

(3)

这意味着振动期间位移振幅的最佳近似值。伽辽金方法的优势在于合理选择位移函数,但应注意随着时间的推移积分的增加,因为加权积分的推广考虑了周期性。特别指出,式(3)是在一个振动周期中添加时间变量的伽辽金方法,是一种扩展的伽辽金方法。式(1)中解的变化为

δq=∑δAncosnωt,

该式为式(2)的变分形式。

δAn通过已知的伽辽金方法,强制加权积分消失,式(3)进一步转化为

(4)

式(4)为关于振幅An和振动频率ω的耦合非线性代数方程组。

2 软铁磁矩形薄板非线性运动方程

考虑磁场环境下,四边简支的软铁磁矩形薄板的长、宽、厚分别为a、b、h,满足厚度远远小于长与宽两者中的最小值。以板的中面作为XY面,建立如图1所示的坐标系。

图1 软铁磁矩形薄板模型

方程的推导基于4个基本假设:

1)计入质量的位移惯性力,不考虑转动惯性力矩;

2)材料在力学性质上可看作弹性、均匀、各向同性材料;

3)材料中无自由电荷、电流存在;

4)中面位移,考虑几何非线性影响。

在矩形薄板中表面建立笛卡尔坐标系。假设中表面上一点的位移分别由X、Y、Z方向上的u、v、w表示。

根据电磁本构关系,对于线性磁化材料:

根据弹性变形理论,薄板运动时,其内部距中面(XOY平面)为u的位移可作如下表示:

(5)

式中i、j、k为单位向量。

将式(5)带入洛仑兹电磁力的表达式,可以得到

式中,f为横向磁场中,单位体积所受的洛仑兹电磁力。

考虑涡电流存在,采用磁偶极子模型[16],并主要考虑薄板Z轴方向的非线性振动,因而此处忽略面内惯性力,可得[17]:

(6)

(7)

式中,ρ为矩形薄板的密度,DM为恒磁场下板的抗弯刚度,DN为恒磁场下板的拉伸刚度,B1z为磁场分布,4为二重Laplace算子,σ为电导率。

由矩形薄板的四边简支条件,采用分离变量法,令Z轴方向位移为

w=∑φi,j(x,y)qi,j(t),

(8)

利用振型叠加法,将满足条件的振型方程的解φ(x,y)设为

(9)

式中,φi,j(x,y)为振型,qi,j(t)为广义坐标,此处仅考虑一阶模态,i、j均取1。

将式(7)—(9)代入式(6),并利用伽辽金积分方法,得到常微分方程:

(10)

式中的参数s1、s2、s3、s4、s5分别为

3 扩展伽辽金法的应用

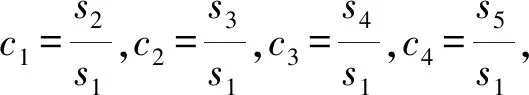
(11)

扩展伽辽金法的使用是针对弱非线性系统,引进小参数ε,式(11)可进一步写为

(12)

方程的渐近解表示为

(13)

其中n和A2j+1是一个整数和振幅。将式(13)代入式(12)得出

根据式(3),可得到加权积分:

即:

通过运算,可以得到:

(14)

(15)

假设初始条件为

(16)

则

A1+A3=A。

(17)

将式(17)代入式(14),

(18)

将式(17)、(18)代入式(15),

通过删除ε的高阶项进行必要的简化,进一步可得到

(19)

将式(19)代入式(18),近似频率解为

为验证其正确性,采用L-P法,设

(20)

将式(20)代入式(12)得出ε不同阶次方程:

(21)

设式(21)通解为

q0=Acos(ωt+β),

令共振项的系数为0,可得

近似频率解为

虽然ε2项有所差别,但精度相同,验证了近似频率解的正确性。

4 结论

1)考虑几何非线性,以及因磁化和涡电流引起的磁场力作用,推导出软铁磁矩形薄板的非线性运动偏微分方程;利用分离变量法及伽辽金法,将系统运动偏微分方程转化为Duffing方程的一般式;基于流行的伽辽金方法,运用了一种求解非线性振动的方法,该方法能很好地逼近固有频率和渐近变形。这些是通过用谐波级数表示变形来实现的,非线性方程在振动的基本周期内通过加权函数和谐波项随时间的积分来近似求解。

2)通过求解非线性方程,可以近似渐近地获得固有频率和振型。该过程实际上是伽辽金方法的扩展,通过在基本振型的一个周期上添加加权函数与时间的积分。同样的程序也可以应用于线性振动方程,以从伽辽金方法中获得相同的结果。伽辽金方法本身和振动周期不仅确保了其有效性,还确保了与微分方程中原始问题的弱形式具有良好的近似性。

3)积分运算的简单性、优雅性、有效性和准确性,特别是使用符号数学工具,为非线性振动分析提供了一种有利且强大的方法,并为更一般的非线性微分方程提供了近似解。