基于分子动力学的熔盐热物性研究进展

付殿威，张灿灿，娜荷芽，王国强，吴玉庭，鹿院卫

（北京工业大学传热强化与过程节能教育部重点实验室，传热与能源利用北京市重点实验室，北京 100124）

目前全球能源结构中，化石能源依旧占据主导地位，但可再生能源在电力系统中的占比不断增大，新型储能技术的发展不断提升[1]。在“双碳”背景下我国加快能源结构转型，大力发展可再生能源，提高可再生能源利用率，努力实现工业的绿色低碳转型并紧跟国家步伐[2]。储能+25特别是储热在可再生能源高效利用中具有重要的作用。熔盐作为高温传热蓄热介质，具有低成本、长寿命、传热储热性能优良的特点，在太阳能光热发电、清洁能源供暖、火电厂灵活性改造等场景中具有广阔的应用前景[3-5]。

根据不同的阴离子种类，熔盐一般可以分为硝酸盐、碳酸盐、氯化盐、氟化盐等。硝酸盐特别是太阳盐(solar salt)被广泛应用在太阳能光热发电系统中[6-7]。碳酸盐的工作范围广，密度大，成本低，在热化学催化反应[8]、燃料电池[9-10]和太阳能制氢[11]中被广泛研究和应用，同时碳酸盐具有相变潜热大的特点，作为高温相变储热材料在高温余热回收利用中具有广阔的应用前景[12-13]。氯化盐的工作温度范围广，成本低，热稳定性好，但是其腐蚀性较强[14-15]。氟化盐具有独特的物理化学性质，在熔盐堆中广泛应用。

前人主要从实验或理论角度对不同种类熔盐的理化性能进行归纳总结，从分子动力学的角度对熔盐理化性能开展研究，可以克服实际情况下难以实现的高温、高压等严峻环境，节省实验时间，减少人为误差。因此本文从分子动力学的角度，对不同类型熔盐(氯化盐、硝酸盐和碳酸盐)的理化性能研究进行分析总结。

1 熔盐分子动力学模型与方法

分子动力学的基本思想是通过设定原子之间的相互作用(势函数)和相关的系综(作用对象和条件)，确定其基本的模拟范畴。首先根据物质建立相关模型，对其设置力场参数和所处环境；其次是计算分子运动路径，获得分子运动中的能量分布；最后分析并计算模型的热力学相关特性，如比热容、热导率、黏度等[16]。图1 所示为熔盐分子模型示意图。图2所示为熔盐分子动力学流程图，首先建立熔盐模型，然后导入编程软件进行计算，计算过程中需要赋予边界条件、力场、势函数、系综等条件，最后对结果进行分析。目前常用的建模软件有Materials Studio(MS)，可以构建晶体结构并赋予相互作用力，再导入编程软件；编程软件有LAMMPS、MATLAB 等；可视化处理软件有Visual Molecular Dynamics(VMD)、OVITO等。

图1 熔盐分子模型Fig.1 Molecular model of molten salt

图2 熔盐分子动力学流程图Fig.2 The flow chart of molten salt molecular dynamics

1.1 势函数的研究进展

分子动力学模拟结果准确性与系统内原子间相互作用势的选取存在直接关系[17]，1924—1984年，学者先后提出了Lennard-Jones(LJ)[18]、Morse[19]、Born-Mayer[20]、 Buckingham[21]、 Busing[22]和Embedded Atom Method(EAM)[23]势函数解析式，为熔盐分子动力学研究奠定了基础。

分子动力学模拟通常选择CVFF (consistent valence force field)力场或者UFF (universal force field)力场。CVFF力场属于传统力场，适用于有机小分子体系，主要预测分子结构和自由能；UFF力场通常适用于所有元素。早期的原子间相互作用势，大多是一些纯经验拟合势，近年来通过对基本电子结构的理论计算，根据对系统总能量的贡献将其分为两类：①总能量由势函数决定，可有效描述范德瓦耳斯互作用占据主导地位的体系；②势函数仅仅描述恒定材料平均密度下系统的能量随原子构型的变化，适用于描述sp-价态金属。本文对熔盐常用的势函数类型、计算公式及对应熔盐进行了总结，如表1所示。

表1 熔盐分子动力学模拟势函数Table 1 Molten salt molecular dynamic simulation potential functions

由表1可以看出，氯化盐常用的势函数为LJ和Born-Mayer-Huggins (BMH)势函数，BMH 势函数排斥力部分利用指数函数，吸引力部分在r-6上再增加一项r-8，效果较好。对于硝酸盐的研究一般使用LJ和Buckingham+Coulomb势函数，其中LJ伴随有长程库仑力，而Buckingham 通过耦合库仑力势函数能更好地模拟硝酸盐理化特性。一般使用BMH 势函数对碳酸盐和氯化盐的理化性能进行研究，它比简单的Born-Mayer 势函数多出了库仑力的计算部分，求解结果更准确。因此选取合适的势函数，可以提高模拟精度。

1.2 参数计算公式

分子动力学计算中用到多种公式，决定分子间的相互作用力。常用的一些公式包括径向分布函数(radial distribution function，RDF)、配位数N(r)、自扩散系数D、均方位移(mean square displacement，MSD)、角分布函数(angular distribution function，ADF)、热导率等，如表2所示。

表2 相关计算公式Table 2 Correlation formula

2 基于分子动力学的熔盐热物性分析

2.1 配位数和自扩散系数

在熔盐分子动力学研究中，配位数和自扩散系数能够表示离子排列的紧密程度，与其黏度、热导率等特性密切相关：自扩散系数越大，导热效果越好，黏度越低；配位数越大，联系越紧密，稳定性越强。利用分子动力学计算熔盐的自扩散系数主要通过计算体系的均方位移(MSD)求得，如表2中式(16)；配位数的计算可通过LAMMPS中的compute coordination/atom命令实现。

对于一元氯化盐，黄世萍等[30]对ZnCl2研究发现Zn2+-Cl-和Cl--Cl-离子间偏径向分布函数与中子衍射的结果与实测值接近，但缺少静电势和近程排斥势以外的势能估算，导致平均距离略高，配位数略低，离子间的排斥势过高。Hazebroucq 等[40]结合密度泛函理论(density functional theory，DFT)，分别对KCl 和NaCl 的配位数及自扩散系数进行研究，发现在结构参数和宏观性能(如自扩散系数)上的结果与先前一些模拟的结果吻合，接近实验数据，证明了分子动力学对熔盐热物性等方面进行研究的适用性。

对于二元氯化盐，Huang 等[41]对ZnCl2-KCl 混合熔盐进行研究，将KCl 颗粒加入ZnCl2熔盐后，Zn2+-Zn2+间近邻距离变化不大，但配位数随着KCl增多显著减少。与此同时，Ding等[42]对不同比例组成的二元NaCl-KCl 熔盐进行研究，发现随着温度的升高，离子团簇之间距离增大，对宏观性能有较大影响。在已有的研究基础上，Xie 等[43]基于有效的BMH 对势模型得出的计算结果与现有实验文献数据基本相同，发现Li+有效地促进了体系的扩散。Rong 等[44]对NaCl-CaCl2的微观结构和热力学性质进行研究，发现在783～1173 K范围内，随温度的升高，配位数小于5时Na+、Cl-离子对分离程度增大，配位数大于5 时分离程度减小；随温度升高，Ca2+、Cl-离子对分离程度增大，配位数小于5时温度越高扩散程度越大，配位数大于5时温度越高扩散程度越小，得到自扩散系数特性如图3所示。

图3 Na+、Cl-离子对和Ca2+、Cl-离子对的扩散程度随温度和配位数的变化：(a) Na+、Cl-离子对；(b) Ca2+、Cl-离子对Fig.3 The variation of diffusion degree with temperature and coordination number of Na+, Cl- ion pairs and Ca2+, Cl- ion pairs: (a) Na+, Cl- ion pair;(b) Ca2+, Cl- ion pair

对于三元氯化盐，Wu 等[25]向LiCl-KCl 共晶体系中加入Na+增强了反离子之间的相互作用，削弱了Cl--Cl-之间的相互作用，K+以原子形态进行扩散，Li+在扩散过程中携带部分配位的Cl-，使扩散物总有效尺寸大于单个离子。姜涛等[45]对LiCl-KCl-CeCl3熔盐中CeCl3的结构性质和热力学特性进行研究，发现单位体积内Ce3+增加，Li+、K+和Cl-离子的扩散阻力增加，自扩散能力降低，导致指前因子减小。

在硝酸盐特别是太阳盐的分子动力学研究方面，Anagnostopoulos 等[46]研究了太阳盐的自扩散系数，与实验数据对比，其误差随温度升高而增加，但趋势相似，如图4所示，高温环境会导致模拟误差增大。Jayaraman 等[47]对太阳盐进行了LJ势和Buckingham 势比较，发现吻合度均较好，且基于LJ势得到的结果与实验数据差异小于17.11%。

图4 自扩散系数随温度变化的实验与模拟对比Fig.4 Comparison of experimental and simulated variation of self-diffusion coefficient with temperature

2.2 熔点

熔点作为熔盐的重要物性之一，对于其工程使用具有至关重要的参考作用。硝酸盐(hitec、hitec XL、solar salt 等)，由于其低熔点和较好的热物性而被广泛使用[48-49]。利用分子动力学计算熔点时，对熔盐梯度升温，每一个温度梯度分别进行NPT系综(等温等压系综)和NVT 系综(正则系综)操作，观察系统达到平衡状态的值。

Wei 等[50]指出目前常用熔盐的凝固点远高于环境温度，直接进行优化会导致运营成本和复杂性增加，可以通过分子动力学模拟预测低熔点熔盐后进行实验验证。He 等[51]利用UFF 力场及LJ 势函数对太阳盐进行研究，发现热膨胀系数随介孔尺寸的增大而减小，熔点随着介孔尺寸的增大先增加后降低。随着温度升高，太阳盐的热膨胀系数逐渐减小，其模拟值与实验值的误差均在2%以内，如表3所示。Ni 等[52]利用Buckingham 势函数以及长程库仑力修复，通过在太阳盐中添加Ca2+发现其熔点最低可降至80 ℃(353.15 K)[53]，黏度增加，离子自扩散系数减小。

表3 熔点随介孔尺寸的变化Table 3 Change of melting point with mesoporous size

基于分子动力学，Jayaraman等[47]利用非平衡方法计算NaNO3的熔点，模拟值与实验值的偏差在±15 K以内，晶、液相之间非常小的自由能差异会导致计算熔点的巨大差异。在现有研究的基础上，Zhang 等[26]利用分子动力学对二元氯化盐(NaCl-KCl)的熔点进行了计算，结果表明随氯化盐纳米团簇尺寸的减小，熔点降低，组分对熔点的依赖性也越发明显，并与纳米团簇尺寸的倒数呈线性关系。

基于前人的研究发现K+和Li+离子的模拟误差比较大，但实际应用中，两者能够有效降低熔盐熔点；Ca2+虽能降低太阳盐熔点，但易与NO3-紧密结合而增加黏度；对熔盐采用纳米团簇的形式会降低熔点，熔点随直径减小而降低。

2.3 比热容

比热容是反映熔盐蓄热能力的重要参数，熔盐比热容可由式(19)计算得出。Ni等[54]研究了NO-2对太阳盐结构和性质的 影响，结果表明，随着NO-2离子簇趋于松散，离子迁移率增大；随着NO-2浓度增加，密度、黏度和比热容降低，热导率增加。

对于Li2CO3-K2CO3二元混合熔盐，Mahtab等[55]发现枝状纳米结构的Li2CO3熔盐能更好地促进比热容的增加以及密度的减少。基于BMH 结合库仑项的有效对势模型，Du 等[56]研究了Na2CO3-K2CO3二元共晶体系的比热容对温度的依赖性，发现离子间的距离是影响热力学性质的主要原因，碳酸熔盐的强共价键C—O具有较高的键能，比热容大于非氧酸熔盐，随温度的变化规律与预期结果一致，误差在9%以内。基于同样的对势模型，Xie 等[43]计算了LiCl和KCl的局部结构和热力学性质，得出的计算结果与现有文献实验数据基本一致，使用BMH 力场可以预测各种氯化熔盐及其混合物的特性，比热容随着Li+的增加而明显增加，误差均在11.1%以内，通过增加粒子数、时间步长来减小误差。在前人的基础上，杨薛明等[57]对KCI、LiCl、NaCl 3种熔盐进行了单独模拟和组合模拟，分别模拟出了一元、二元和三元混合熔盐状态下的热物性参数。3 种单质熔盐的比热容模拟结果与实验值的误差均在6.8%以内，熔盐比热容、黏度及热导率在其熔融状态下，随着温度的升高而下降，体系结构变得松散，且在多元混合熔盐中随着LiCl混合比例的增加，比热容增加。

通过分子动力学模拟得到的比热容结果与实验数据对比，发现硝酸盐的误差最小，碳酸盐次之。在硝酸盐中随着NO-2浓度的增加，其比热容降低；对于氯化盐，Li+离子浓度的增加会导致比热容提高，有效促进系统的扩散，K+离子数量越多，比热容误差越小。

2.4 热导率

热导率是熔盐传热能力的重要指标，提高热导率可以提升熔盐储/放热效率。熔盐热导率可由式(22)、式(23)计算得出，采用非平衡动力学比平衡动力学精度高。Anagnostopoulos 等[46]利用分子动力学研究了太阳盐的热导率等特性，发现其热导率的模拟数据与实验数据接近。

在碳酸盐研究方面，基于BMH 结合库仑项的有效对势模型，Du 等[56]模拟了Na2CO3-K2CO3二元共晶体系在1000～1400 K 范围内的热导率对温度的依赖性。与此同时，基于Tosi-Fumi 修改后的BMH 势，Ding 等[58]对Na2CO3和K2CO3的热导率进行了模拟，发现其热导率与已有文献中的实验数据吻合较好。

在氯化盐研究方面，Xie 等[43]基于已有文献，对LiCl-KCl研究发现其热导率随着Li+的增加而明显增加。在前人的基础上，杨薛明等[57]对KCI、LiCl、NaCl 3种熔盐，分别进行了单质与混合的分子动力学模拟。3种熔盐单质的热导率模拟数据与实验对比，除LiCl 外，误差均小于9%；随着LiCl 混合比例的增加，其热导率呈上升趋势；熔盐热导率随温度升高而下降，如图5所示。Manga等[59]研究发现在ZnCl2-NaCl-KCl三元氯化盐中，KCl提供了高导热特性，且热导率与温度表现出正相关性。

图5 不同比例LiCl对热导率的影响Fig.5 Effect of different ratios of LiCl on thermal conductivity

综上所述，基于分子动力学的硝酸盐热导率误差均小于10%，碳酸盐中包含Na+离子时的热导率误差在2%以内。当加入K+、Li+离子后误差急剧增大；氯化盐中Li+离子浓度的增加会导致热导率提高。

2.5 黏度

黏度指流体对流动所表现的阻力，利用分子动力学将系统分为高速区和低速区，通过两区域交换粒子动量获得黏度。Ruan 等[60]采用分子动力学模拟和第一性原理相结合的方法，验证了原子单位为250 个时可以计算其黏度。Anagnostopoulos 等[46]研究发现太阳盐的黏度与实验值具有较好的一致性，如图6 所示。Ni 等[52]发现在太阳盐中添加Ca2+离子，黏度升高，自扩散系数降低，原因是Ca2+的配位壳中原子排列更紧密规律，导致与NO3-的强键作用，使NO3-离子无法轻易脱离躯体。随着Ca2+数量的增加，网络结构增长并延伸到整个系统，限制了系统中离子的运动，引起黏度增强，如图7所示。

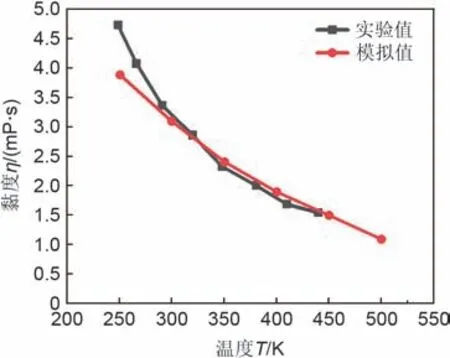
图6 黏度随温度变化的实验与模拟对比Fig.6 Comparison of experimental and simulated variation of viscosity with temperature

图7 不同Ca2+离子浓度下黏度随温度变化对比Fig.7 Comparison of viscosity variation with temperature at different Ca2+ concentrations

在碳酸盐研究方面，Du等[56]发现Na2CO3-K2CO3二元共晶体系的黏度模拟结果与实验误差在9%以内，其随温度的变化规律与实验结果一致。基于修改后的BMH势，Ding等[58]对Na2CO3和K2CO3的黏度、密度研究，发现其黏度与已有实验数据吻合较好，密度模拟计算结果与实验数据误差在10%以内。在氯化盐研究方面，杨薛明等[57]对KCI、LiCl、NaCl 3种熔盐进行组合模拟，发现KCl-LiCl二元熔盐黏度随KCl 增加而升高。Manga 等[59]研究发现ZnCl2-NaCl-KCl 熔盐中随着LiCl 混合比例的增加，黏度整体呈现下降趋势，且体系结构变得松散。作为未来的黏度研究方向，采用MATLAB与LAMMPS耦合的黏度计算方法，可以实现更高的计算精度。

3 结论与展望

本文对基于分子动力学的熔盐(硝酸盐、碳酸盐和氯化盐)热物性研究现状进行分析，对熔盐分子动力学势函数进行总结归纳，主要结论如下：

（1）采用分子动力学可以有效地模拟计算熔盐热物性，但分子动力学模拟存在一定的不确定性，不同类型的熔盐所采用的模拟计算方式不一致。针对硝酸盐更适合使用带有库仑力的Buckingham势，碳酸盐和氯化盐更适合使用BMH 势计算来减小模拟误差。

（2）在计算含有Li+的熔盐熔点、比热容和热导率时模拟误差偏大，目前对含有Na+、K+、Li+的熔盐分子动力学研究相对较多，缺乏对含有Zn2+熔盐的相关研究；加入Ca2+可以降低太阳盐的熔点，但会增加其黏度。在硝酸盐中，随着NO-2浓度的增加，其比热容降低。对于氯化盐，Li+离子浓度的增加会导致比热容、热导率提高，有效促进系统的扩散，但会使误差增大；K+离子浓度增加会促进系统扩散，除比热容外，其余物性误差增大，通过增加整体离子数、时间步长可以减小其计算误差。对于碳酸盐的研究发现模拟误差普遍较小，模拟结果与已有文献中的结果吻合较好。

（3）在熔盐分子动力学研究中，K+、Li+等对模拟结果误差影响较大，可以通过增加整体分子数量、校正位能截断距离、增加模拟时间步长等方法来减小误差；为消除边界效应以及防止粒子丢失，引入周期性边界条件，截断半径外的长程库仑力可采用PPPM (Particle-Particle-Particle Mesh，使用离散傅里叶变换来计算Ewald 加和的倒易空间部分，提高大体系Ewald加和的速度，从而提高处理大规模带电体系时的计算效率）的方法计算来减小误差。同时模拟环境与实际情况并不完全相同，探究纳米流体对熔盐分子动力学的影响、降低分子动力学模拟误差、开展基于分子动力学的熔盐腐蚀特性研究可以作为下一步熔盐分子动力学的研究方向。