基于数学史的数学文化融入高三数学单元复习课的教学研究

2023-12-19黄思婷朱哲

中学数学杂志(高中版) 2023年6期

黄思婷朱哲

【摘要】明晰基于数学史的数学文化内涵、数学史融入数学教学的运用方式，构建基于数学史的数学文化内涵下的单元复习课教学.在不同内涵维度下，选择合适的单元复习课主题，于对应专题中选取适当的高考真题、历史名题及改编题等，用知识主线、方法策略、核心素养等进行串联，以期进一步提升基于数学史的数学文化融入数学教学的教育价值.结合相关教学案例，对提高教师文化素养、系统研究理论文献、深入开展教学实践等提出思考与展望.

【关键词】数学史；数学文化；单元复习课；数学教学

2020年，教育部考试中心发布高考试题命制要以“一核四层四翼”为基本内涵，关注数学本质，厚植爱国情怀，对“立德树人”起到正确导向作用.“立德树人”价值导向下的数学教学应该是充满文化氛围，拥有强大生命力的.《普通高中数学课程标准（2017年版）》中定义数学文化是数学的思想、语言、方法等及其形成和发展，是人类文化的重要组成部分［1］.其中数学史是数学文化的重要载体，实践表明数学史融入数学教学，能引导学生从数学孤岛到充满生机和趣味的数学大陆上，有助于构建知识之谐，彰显方法之美，营造探究之乐，达成能力之助，展示文化之魅，促成德育之效［2］.单元复习课强调整体教学观，即整体把握数学知识的本质，串联与内化思想、方法和策略，提升思维、能力和素养，进一步实现教育价值.基于数学史的数学文化融入单元复习课的教学研究，以期在数学文化浸润、核心素养聚焦中既实现专题复习，又深刻揭示冰冷数学背后的火热思考.1 基于数学史的数学文化融入教学的框架

参考相关文献，认识基于数学史的数学文化的内涵，了解数学史融入数学教学的运用方式，以期进一步实现数学文化在数学教学中的教育价值.1.1 基于数学史的数学文化内涵分析框架

汪晓勤团队［3］结合质性研究法，并征询专家组成员意见，反复归纳、修改，得到“基于数学史的数学文化”内涵分析框架，其中包括知识源流、学科联系、社会角色、审美娱乐、多元文化五个维度（见图1）.该框架既扎根于新课程标准的要求，又为数学文化融入数学教学提供指导，联结理论与实践，具有一定的客观合理性.

1.2 数学史融入数学教学的运用方式

汪晓勤团队［4］在原有基础上整合我国数学教学特点，进一步改进，得到数学史融入数学教学的四种运用方式：附加式、复制式、顺应式和重构式（见表1）.其中四种运用方式没有水平高低之分，具体选择哪种，取决于所要达到的教学目标.

2 基于数学史的数学文化融入单元复习课的教学案例

参考相关文献梳理基于数学史的数学文化内涵的定义、作用及教学建议，设计或借鉴数学史融入复习课教学的相关案例并进行简析，帮助理清其内涵及与教育价值的关系.

2.1 知识源流2.1.1 知识源流的内涵及作用

知识源流指知识的来源与应用，其中大致包括人物与事件的关联和发展、概念与术语的起源和应用、命题与证明的因果和联系、问题与求解的表述和应用四个子维度［3］.知识源流由时间纵向研究数学文化，注重研究的深度，嘗试从数学内部探求数学中的文化.2.1.2 知识源流内涵下的复习课教学

知识源流内涵下的复习课教学可结合教科书或高考真题，寻本溯源，用附加式补充概念等来源及应用，并结合顺应式用问题串引导学生层层探索，构建问题框架，帮助学生形成知识或解法新图式和新模型，并将其纳入原来知识体系中.好题难得，教师可扎根数学名著，精选数学名题，并尝试命制将数学史从显性或隐形角度融入的试题.2.1.3 知识源流内涵下的案例及简析

案例1 圆锥曲线单元复习课——“动点的轨迹”专题.

环节①：问题探究例1 已知正方体ABCD－A1B1C1D1的棱长为3，M在CC1上，CM=1，动点N在面CDD1C1上运动，当N在平面A1BM内时，N的轨迹长度为.当AN=21时，N的轨迹长度为.环节②：文化研析（2014·湖北文17）已知圆O：x2+y2=1和A（－2，0），若B（b，0）（b≠－2）和常数λ满足：对圆O上任意一点M，都有MB=λMA，则b=，λ=.

数学史补充数学家阿波罗尼斯在《平面轨迹》中研究了大量平面轨迹（直线和圆），其中“阿波罗尼斯圆”是其代表作，即平面上一点P到两定点A、B的距离之比满足PAPB=λ（λ>0且λ≠1）为常数，则P的轨迹是圆.（2008·江苏13）满足条件AB=2，AC=2BC的△ABC面积的最大值是.

环节③：类比求解变式：已知F1（－2，0），F2（2，0），动点P到y轴的距离与它到F1，F2距离之差的绝对值的比值为34，求P的轨迹方程.

数学史补充古希腊数学家帕普斯在《数学汇编》中研究一类新的轨迹问题，即“n线轨迹（n≥3）”问题，费马和笛卡尔在研究古希腊“n线轨迹”问题时发明了解析几何.

案例简析结合数学文化的知识源流、社会角色内涵展开案例研究，“动点的轨迹”可作为圆锥曲线单元复习的起始专题课.教学围绕动点相关问题，串联直线与圆、圆锥曲线两大知识体系，体现知识之谐、方法之美.教学引导学生构建“动点到一定点的距离——到两定点的距离之比——到两定点、一直线的距离之比”的新图式，类比探究，体现能力之助、探究之乐.用附加式补充相关数学史，改编历史素材或历史名题，用顺应式将圆、圆锥曲线等数学史串联其中，体现文化之魅.教学顺序可帮助学生感悟曲线的发展历程，尝试将历史序、逻辑序与学生的心理序相统一，增强学生学习数学的兴趣，体现德育之效.

2.2 学科联系2.2.1 学科联系的内涵与作用

学科联系指借助数学史这一桥梁，联结数学与物理、天文等学科的知识脉络，通过跨学科的文化交融来演进社会发展.学科联系内涵下的复习课案例富有创造性，跨学科的案例较注重数学的应用性与社会价值，给人眼前一亮的感觉.

2.2.2 学科联系内涵下的复习课教学

学科联系内涵下的复习课教学可借助复制式或顺应式，从真题或改编题丰富的背景中感受数学与其他学科的联系，其中应重点关注将文字语言转化为数学语言.也可结合STEAM实验教学，以数学史为基础，实验为纽带，学科联系为导向，在STEAM新视野下展开教学案例设计［5］.学科联系维度下的复习课教学难度较大，还需在已有案例研究的基础上继续开展系统的实践研究.

2.2.3 学科联系内涵下的案例及简析

案例2 立体几何单元复习课——“鳖臑”专题.

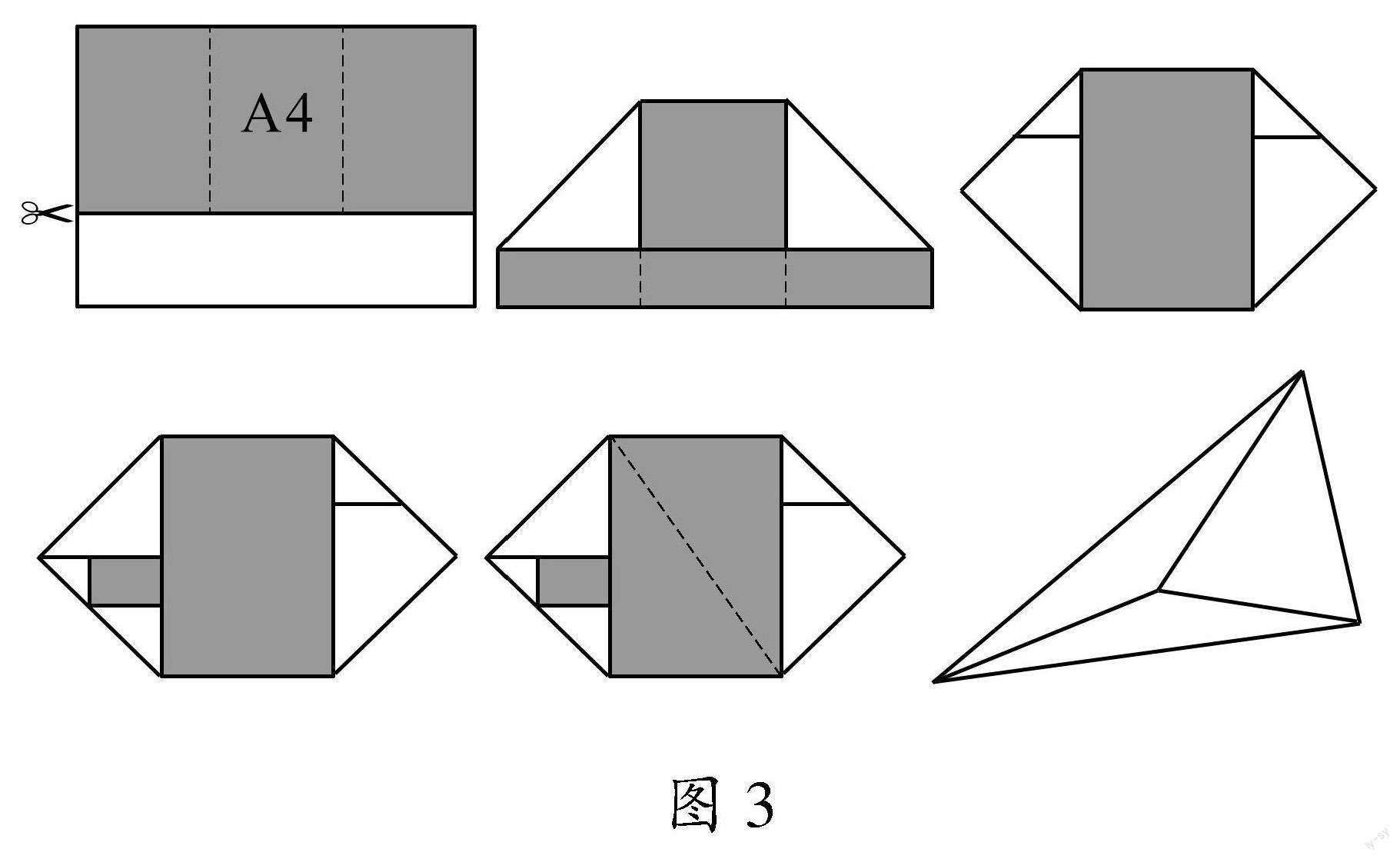
环节①：折纸呈模型

呈现折叠过程：

环节②：几何现鳖臑

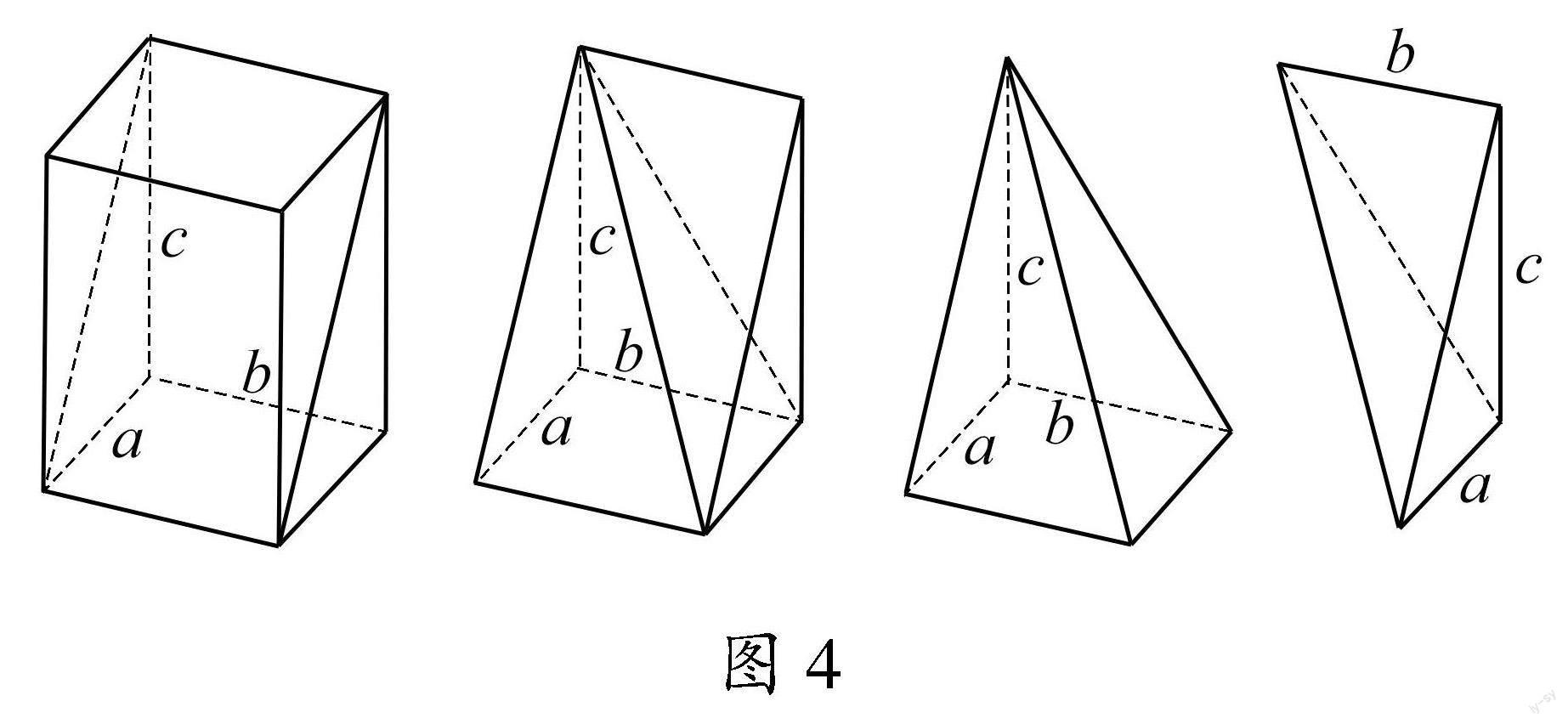
数学史补充鳖臑最早出现在《九章算术》中，“此术臑者，背节也，或曰半阳马，其形有似鳖肘，故以名云.”现在通常定义鳖臑是四个面都是直角三角形的四面体.

刘徽分长方体的过程，左至右（第二幅图起）分别为壍堵、阳马和鳖臑.

环节③：教学显价值

结合高考真题，从领悟垂直关系、掌握“补形”技巧、沟通三类空间角三个方面开发鳖臑体的教学价值，进一步发展学生直观想象和逻辑推理等核心素养.

案例简析本案例结合《从STEM教育视角看折纸》［6］和《鳖臑搭起发展直观想象素养的“脚手架”》［7］，常文武、丁少杰等老师结合数学文化的学科联系、审美娱乐、知识源流、社会角色内涵展开案例研究，“鳖臑”可作为立体几何单元复习的一个专题.这节课教学紧扣“鳖臑”这一大概念，充分阐述是什么（具体与历史模型）和怎么样（应用与教育价值），体现知识之谐、文化之魅.用附加式展示数学史，用顺应式改编数学史料并将其融入试题，结合鳖臑体直观解决问题，体现方法之美、探究之乐.教学从动手操作（折纸）开始，由实际模型中加深对鳖臑体的抽象体验，从鳖臑体的点、线、面关系探索其具体应用，发展学生直观想象和逻辑推理等核心素养，体现能力之助、德育之效.

2.3 社会角色2.3.1 社会角色的内涵与作用

社会角色主要指数学的应用价值，“广泛应用性”是数学的基本特点之一.将数学史融入数学教学的案例基本都涉及该维度，古今数学应用相联结，既可窥探社会发展的演进，也为数学有用论再一次正名.

2.3.2 社会角色内涵下的复习课教学

社会角色内涵下的单元复习课教学可用附加式展示数学在社会生活等领域的广泛应用，用复制式直接沿用历史名题，用顺应式改编历史素材或名题，以串联古今中外的数学应用.社会角色内涵下的复习课教学既能揭示数学的应用性及社会价值，也能内化数学的文化价值.2.3.3 社会角色内涵下的案例及简析

案例3 ; 数列单元复习课——“斐波那契数列”专题.

环节①：回归课本

人教A版普通高中數学教科书（选择性必修第二册）“4.1数列的概念”在“阅读与思考”中详细介绍斐波那契数列.

问题1：根据斐波那契数列的定义，求其递推公式与通项公式？

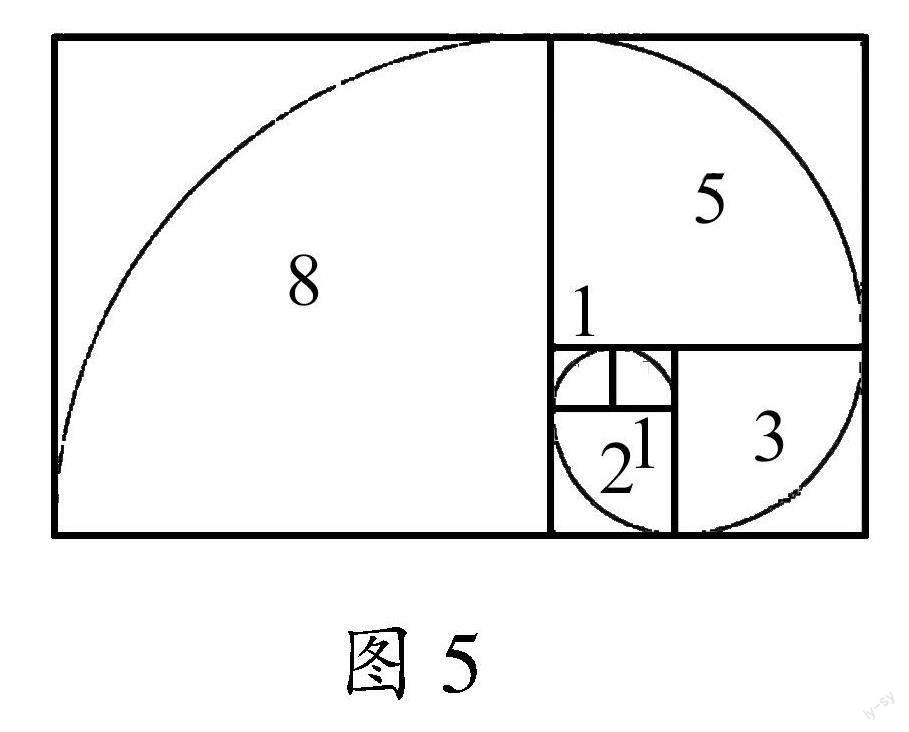
图5环节②：讲解性质

结合斐波那契数列的广泛应用性，如“斐波那契螺旋”，向日葵中小花的排列等讲解相关性质.

环节③：试题解析

从中选取一道例题感受斐波那契数列的广泛应用性.

例1 阶梯教室共10级台阶，设每次只迈1个台阶或2个台阶，从下面的台阶到最上面的台阶，共有多少种不同的走法？

案例简析本案例选自《高三数学复习教学与拓展——以斐波那契数列为例》［8］，庞志雷老师结合数学文化的社会角色、审美娱乐、知识源流内涵展开案例研究，“斐波那契数列”可作为数列单元复习的一个专题.这节课教学紧扣“斐波那契数列”这一大概念，回归课本，引导学生利用教科书关注相关扩展知识是什么、为什么、怎么样，体现知识之谐、能力之助.结合斐波那契数列的广泛应用性，借助图形直观分析其性质，体现探究之乐、文化之魅.教学引导学生利用该扩展知识解决实际问题，锻炼其阅读理解、归纳猜想等思维能力，提升数学抽象、逻辑推理等核心素养，体现德育之效.

2.4 审美娱乐2.4.1 审美娱乐的内涵与作用

审美娱乐主要指数学美和趣味数学.数学美横跨“文化中的数学”与“数学中的文化”，数学的对称美、统一美等通过教学得到外显，助力美育的完善.趣味数学展现数学有趣，培育智力发展，将历史、文化与数学相结合，相辅相成即可受益良多.

2.4.2 审美娱乐内涵下的复习课教学

审美娱乐内涵下的复习课教学可从高考真题出发，用附加式、复制式、顺应式等方式融入数学史展示数学美和趣味数学.审美娱乐内涵下的单元复习课教学引导学生用欣赏的眼光观察，用数学的思维思考，并用数学符号表达，从而提升相关数学核心素养.

2.4.3 审美娱乐内涵下的案例及简析

案例4 立体几何单元复习课——“体积”专题.

图6环节①：感受文化

（2017·江苏理6）在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切.记圆柱O1O2的体积为V1，球O的体积为V2，则V1V2的值.

数学史补充古希腊数学家阿基米德发现圆柱体的体积比其内切球的体积为3∶2，阿基米德的墓碑上即刻着“圆柱容球”与“3∶2”，以纪念阿基米德在几何上的伟大发现.

图7（2013·上海13）在xOy平面上，将（x－1）2+y2=1（x≥1）和（x－3）2+y2=1（x≥3）、y=1和y=－1围成的封闭图形记为D.记D绕y轴旋转一周而成的几何体为Ω，过（0，y）（|y|≤1）作Ω的水平截面，所得截面面积为4π1-y2+8π，试利用祖暅原理，得到Ω的体积为.

数学史补充古代数学家祖暅提出祖暅原理“幂势既同，则积不容异”，这对微积分的建立产生重大影响，且晚了1100多年意大利数学家卡瓦列里才提出相似的卡瓦列里原理.

环节②：研析文化

引导学生从真题来源、呈现方式两方面分析数学史融入高考真题.

环节③：运用文化

设计活动：认识几何体、深度探究、本源探寻、对接真题.

案例简析本案例选自《高三复习融入数学文化的一点尝试》［9］一文，丁益民老师结合数学文化的审美娱乐、知识源流、多元文化、社会角色内涵展开案例研究，“体积”可作为立体几何单元复习的一个专题.这节课教学紧扣“体积”这一大概念，梳理与构建公式法、割补法、模型法的新图式求体积，体现知识之谐.用顺应式改编真题，用复制式和顺应式结合引导学生研究鳖臑体并解决问题，体现方法之美，探究之乐.教学引导学生从高考真题中感受美、欣赏美，追本溯源去窺探中外数学文化的璀璨，体现文化之魅.同时教学也始终把握数学本质，引导学生用数学思维分析，用数学语言表征，结合数学运算解决问题，从而培养相关能力与提升相应素养，体现能力之助和德育之效.2.5 多元文化2.5.1 多元文化的内涵与作用

多元文化指不同时空下于同一数学主题的交汇与碰撞.多元文化关注时间纵向与空间横向的发展，多元文化属于文化比较，可从数学外部认识文化中的数学.在多元文化浸润中，学生可真切感受数学的发展与演进，完善正确历史观，提升民族文化自信.

2.5.2 多元文化内涵下的复习课教学

多元文化内涵下的复习课教学可用附加式、复制式、顺应式等方式在教学中融入数学史，引领学生感受数学家对同一数学知识的贡献，从不同中找认同，发展“中国认同”.同时在教学中体验数学家对同一数学知识的研究历程，从不同中找相同，建立动态的数学观.2.5.3 多元文化内涵下的案例与简析

案例5 解三角形单元复习课——“解三角形的应用”专题.

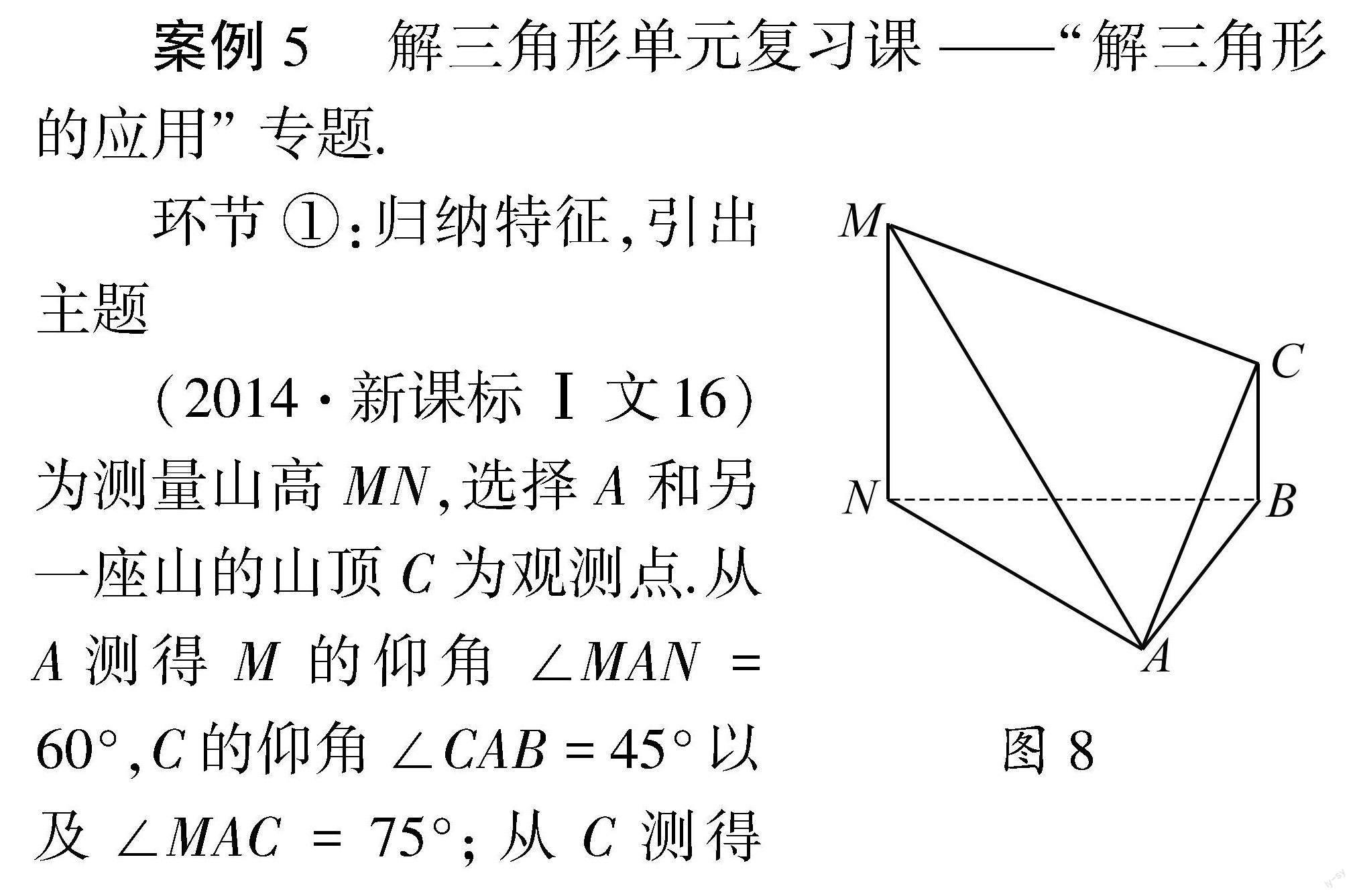
图8环节①：归纳特征，引出主题

（2014·新课标Ⅰ文16）为测量山高MN，选择A和另一座山的山顶C为观测点.从A测得M的仰角∠MAN=60°，C的仰角∠CAB=45°以及∠MAC=75°；从C测得∠MCA=60°.已知山高BC=100 m，则山高MN=.

环节②：追忆历史，寻找源头

数学史补充三国时代数学家刘徽著《海岛算经》一书，收录9个测量问题，涉及海岛高、河宽等问题.

用相似三角形法、杨辉的“重差”法解《海岛算经》第一个问题，作比较，找同与不同，补充国外数学家（如印度数学家阿耶波多、德国数学家皮蒂克斯等）对测高研究的数学史.

环节③：古今联系，合作探究

优化古代方法，结合现代知识对一个问题进行一题多解，并相互评析.

案例简析本案例选自《HPM视角下的“解三角形的应用”专题复习课》［10］，赵玉梅老师结合数学文化的多元文化、学科联系、社会角色、知识源流、审美娱乐内涵展开案例研究，“解三角形的应用”可作为解三角形单元复习的一个专题.教学沿着“为什么—怎么做—是什么—优化怎么做”路径展开，从知识由来到用知识解决实际问题，体现知识之谐和能力之助.用附加式介绍三角学相关内容，用复制式展现数学家测高方法，用顺应式让学生自主探究测高，内化最优解，体现方法之美、探究之乐和文化之魅.教学通过比较数学家对同一问题的解法，学生可深刻感受中国古代数学家的探究与坚持，提升民族自豪感，体现德育之效.3 思考与展望

基于数学史的数学文化融入单元复习课教学，旨在构建基于数学史的数学文化内涵框架下的单元复习课，尝试将适当的数学史素材用合适的运用方式融入数学教学.结合以上案例可知，基于数学史的数学文化内涵下的数学教学均能实现一定的教育价值.

数学文化融入数学教学，教师应对数学文化的内涵有较为清晰的认识，拓宽数学文化面，选择合适的素材，并用合适的运用方式将其融入，以期在实践中进一步提升学生的数学素养.在HPM（数学史与数学教学的关系）视角下，数学史融入单元复习课的相关案例虽目前数量较少，五个维度也分布不均，相比较知识源流、社会角色维度下的案例略多于学科联系、审美娱乐、多元文化维度下的案例，但一线教师等对案例的探索与实践从未止步［11］.基于数学史的数学文化内涵维度下的单元复习课教学，要体现知识之谐、方法之美、探究之乐、能力之助、文化之魅、德育之效，并通过内化科学、应用、文化、审美价值，最终实现立德树人的教育价值，这些均需对已有理论、高考真题、教学案例等进行深入且系统的文献与实践研究.

参考文献

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版）［M］.人民教育出版社，2018.

［2］王鑫，岳增成，汪晓勤.HPM研究的框架与进展［J］.数学通报，2021，60（06）：7-12+19.

［3］余庆纯，汪晓勤.基于数学史的数学文化内涵实证研究［J］.数学教育学报，2020，29（03）：68-74.

［4］汪晓勤.HPM的若干研究与展望［J］.中学数学月刊，2012（02）：1-5.

［5］林庄燕，姜浩哲.学科史视角下的中学STEAM实验教学设计［J］.中小学实验与装备，2019，29（04）：4-6.

［6］常文武.从STEM教育视角看折纸［J］.教育研究与评论（中学教育教学），2019（02）：39-42.

［7］丁少杰，杨亢尔.鳖臑搭起发展直观想象素养的“脚手架”［J］.中学教研（数学），2022（03）：11-14.

［8］庞志雷.高三数学复习教学与拓展——以斐波那契数列为例［J］.青海教育，2018（06）：41-42.

［9］丁益民.高三复习融入数学文化的一点尝试［J］.数学通讯，2021（09）：1-4.

［10］赵玉梅.HPM视角下的“解三角形的应用”专题复习课［J］.数学教学，2020（05）：44-50.

［11］汪晓勤.基于数学史的数学文化内涵课例分析［J］.上海课程教学研究，2019（02）：37-43.