反旋双色椭圆偏振激光脉冲驱动的氩原子非次序双电离对椭偏率的依赖

黄诚，苏杰，廖健颖，刘子超，贺佟佟，李盈傧

（1 西南大学 物理科学与技术学院，重庆 400715）

（2 信阳师范学院 物理电子工程学院，信阳 464000）

0 引言

当一个原子处在超快超强激光场中时，该原子首先被激光电场剥离一个电子，而后该电子在激光场的作用下在空间中随激光电场自由振荡，该自由电子有一定的概率被电场拉回母离子附近与母离子发生相互作用，即再碰撞［1］。在此过程中，返回电子将其在电场中积累的部分动能转移给另一束缚电子，使该束缚电子具有足够的能量挣脱母离子的束缚发生电离［2-6］。在对二价离子产量的测量中发现强度依赖的离子产量曲线呈现出了一个膝盖状的结构［7］。该结构反映了二价离子的产量比两电子次序电离理论预测的要高几个数量级，这一反常的强场双电离现象被称为非次序双电离（Nonsequential Double Ionization，NSDI）［8-9］。在NSDI 中两电子存在强烈的关联性［10-12］，这种关联性直观地体现在电子的末态动量分布上。所以分析末态电子动量关联分布并探究导致如此关联行为的电子超快动力学过程一直是过去三十年NSDI 研究的热点［13-19］。

近年来人们利用二维复合电场来驱动原子中的电子电离和返回，进一步诱导NSDI 的发生。单个的圆偏或椭偏激光场是最简单的二维电场。与线偏光情况相比，圆偏或椭偏激光场驱动的NSDI 表现出更加丰富有趣的现象，比如：椭偏场中再碰撞更可能发生在椭圆长轴方向电场零点之后［20］；低强度下椭圆长轴方向的电子释放呈现出反关联特性，且随椭偏率增加反关联特征越强［21］；圆偏光场中初始电子相对于激光场矢势旋转方向的不同会导致高达一个数量级的电离产量的差别［22］。由两个频率不同旋转方向相反的圆偏振脉冲则能组成更加复杂的二维复合电场，该反旋双色圆偏（Counter-rotating Two-color Circularly Polarized，CTCP）场的波形具有多重空间对称性，电离电子可以从几个特定的方向返回，最终电子动量分布也展现出了多重对称性。参与叠加的两圆偏脉冲的参数变化能够显著地影响复合激光电场的波形，进一步影响NSDI的动力学和电子关联特性。比如，两脉冲的幅值比可以有效控制NSDI 的产量和电子的返回能量［23-27］，两脉冲的相对相位会影响电子的返回方向和分子的双电离概率［28-29］，激光强度会影响电子碰撞的次数［30-31］。先前的研究也发现CTCP 场中NSDI 的两电子之间也展示出了强烈的角关联［32-33］。对CTCP 场中NSDI 的研究揭示了丰富的电子动力学。XU T T 等研究了一个圆偏加一个椭偏脉冲组成的复合场中的NSDI，发现Ar的NSDI概率随椭偏率的增加而增加，而Mg 的NSDI 概率不依赖椭偏率［34］。进一步，两个频率不同的反向旋转的椭圆偏振激光脉冲组成的复合光场也被用来驱动原子产生高次谐波［35-36］、分子解离［37］和诱导NSDI［38］。该反旋双色椭偏（Counter-rotating Two-color Elliptically Polarized，CTEP）场不具有CTCP 场那样的多重空间对称性［39-40］，所以电子的返回方向和最终动量分布也不具有对称性。本文课题组先前研究了固定两脉冲的椭偏率为0.3 条件下两个椭偏场之间的相对相位对NSDI 的影响［38］。本文将系统地研究两脉冲椭偏率对CTEP 场中原子NSDI概率和离子动量分布的影响，并探究其中电子电离的动力学过程。

1 理论方法

研究强激光场中原子的NSDI 需要处理的是一个原子核和两个电子组成的三体量子系统，要精确地描述该系统的演化需要求解两电子的全维含时薛定谔方程。两电子在强激光场中运动的空间范围很大，全维量子计算需要极大的计算资源，目前仅能完成短波长线偏振的情况。对于本文面对的复杂的二维电场的全维量子计算已经超出了目前的计算能力。对于这种情况，强场电离领域通常采用经典系综方法来处理［41-46］，这样不仅可以极大地减小计算量，同时也能够直观地展示电离电子的运动轨迹。虽然经典系综模型计算的结果无法与特定原子的实验数据和求解全维含时薛定谔方程的结果达到定量的一致，但是大量的研究表明经典系综模型能够定性地再现NSDI 的再碰撞过程、电子关联特性及其对激光参数的依赖。因此，本文采用全经典系综模型［41］来研究CTEP 激光场中Ar 原子NSDI 的椭偏率依赖。在这个模型中，两电子的演化遵循牛顿运动方程

式中，下标i用于标记两个电子的序号。r1和r2为两个电子坐标。表示电子i与原子核之间的相互作用。软核参数a的设置是为了避免经典原子中的电子自电离。为了避免一个电子落入较深的势阱而导致另一个电子自电离，所以a有一个下限值，保证势阱不能太深。当然，如果a值太大，势阱太浅，则势阱中无法容纳两个电子且要保证他们的经典势能小于两电子电离能的相反数，这就决定了a的上限［47］。结合这两个因素，为了获得一个稳定的经典的两电子系统，对于Ar 原子通常a取1.5。表示两电子之间的相互作用，其中软核参数b是为了避免数值计算的奇异性，任意一个较小的数值均可，这里取值0.05。CTEP 复合电场E（t）=Er（t）+Eb（t），其中Er（t）和Eb（t）分别为1 600 nm和800 nm 脉冲的椭偏电场。1 600 nm 电场顺时针旋转，800 nm 电场逆时针旋转。两椭圆激光场的长轴都沿x方向。两电场的表达式为

式中，εr和εb为1 600 nm 和800 nm 脉冲的椭偏率，ω表示1 600 nm 脉冲的角频率。电场幅值E0对应的激光强度为3×1013W/cm2。ƒ（t）为激光脉冲包络，这里整个脉冲的包络为梯形，全宽为10T（T为1 600 nm 激光场的周期），其中6T的平台区，2T线性开启和2T线性关闭。

首先将两个电子放置在母离子附近且经典允许的位置，基于放置的位置坐标，计算出母离子和两个电子组成的三体系统的整体势能，然后给系统添加一个特定的动能，使得整个系统的总能量等于-1.59 a.u.（对应Ar 原子的第一电离能和第二电离能之和）。该动能被随机的分配给两个电子，同时随机给定两个电子的动量方向。然后以这个给定的位置和动量为初始条件，让两电子仅在库仑作用力下演化一段时间，从而获得稳定的位置和动量分布。以此作为初始系综，紧接着将该系综在库仑场和CTEP 场的共同作用下演化至脉冲结束。演化结束后，如果两个电子的末态能量都大于零，则认定双电离发生。

2 结果与讨论

图1 是不同椭偏率下复合电场E（t）（虚线）和相对应的负矢势-A（t）（实线）。每一个周期的电场分为三个波瓣，他们对应负矢势三条边。图中的空心方块和实心圆标出了电场最大值和对应的负矢势。箭头表示时间演化方向，电场演化从波瓣1（蓝色），波瓣2（红色）到波瓣3（绿色），负矢势演化从边1（蓝色），边2（红色）到边3（绿色）。与CTCP 场不同，CTEP 场的复合电场不具有三重对称性，如三个波瓣的形状和幅值都不相同，他们两两之间的夹角也不相等。矢势也不再具有三重对称性，如电场波瓣2 和波瓣3 的最大值对应的负矢势并不在边2 和边3 的中间位置。随着两脉冲椭偏率的增大，复合电场和负矢势在y方向的分布范围逐渐扩大。

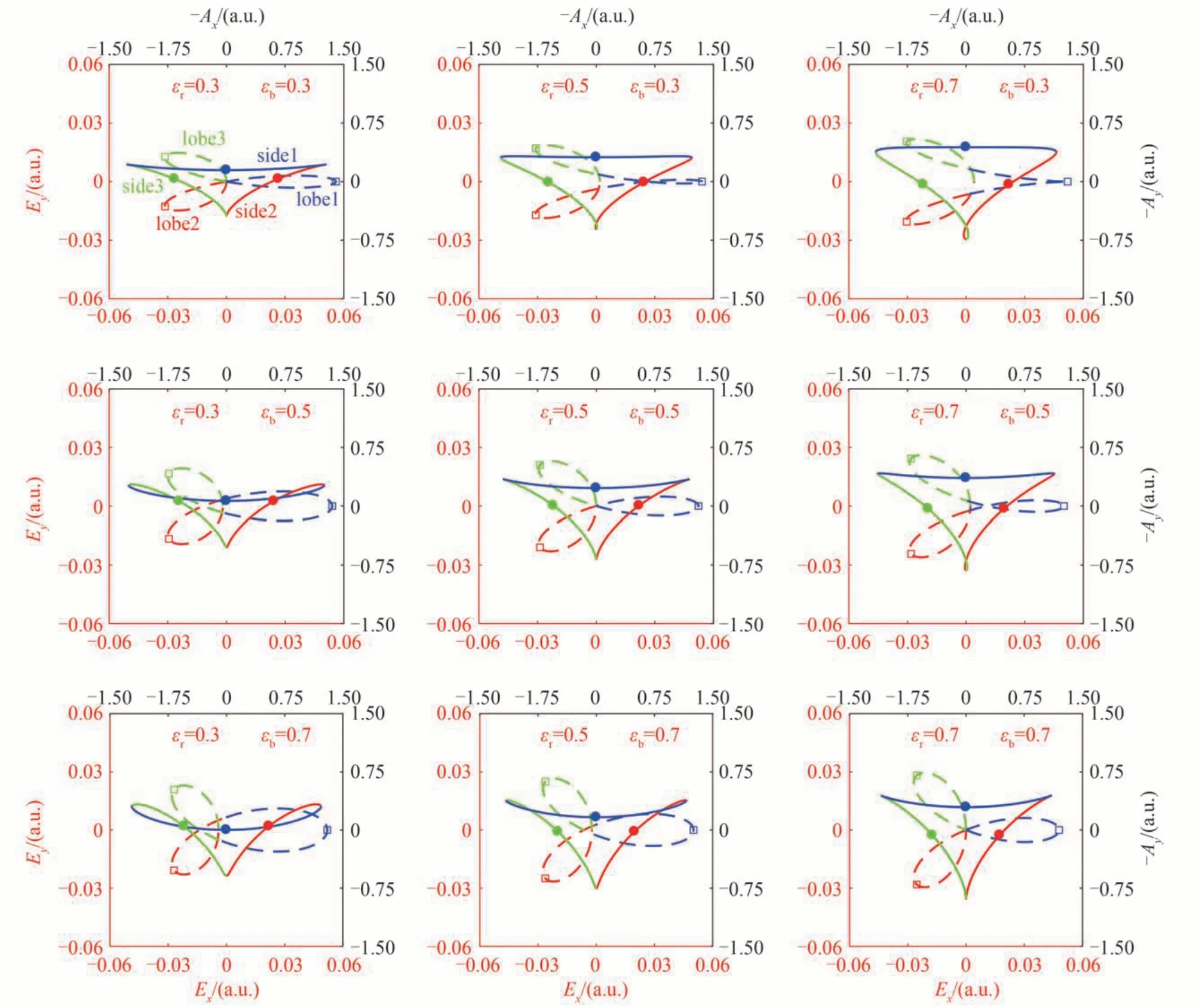
图1 不同椭偏率下CTEP 复合电场E（t） （虚线） 和相应的负矢势-A（t） （实线）Fig.1 Combined electric fields E（t） （dashed line） and corresponding negative vector potentials -A（t） （solid line） for different ellipticities

图2 是不同椭偏率下CTEP 激光场中Ar 原子NSDI 概率。当固定1 600 nm 脉冲的椭偏率时，NSDI 概率随着800 nm 脉冲椭偏率的增大而逐渐增大。当固定800 nm 脉冲的椭偏率时，NSDI 概率随着1 600 nm 脉冲椭偏率的增大而逐渐减小。εr=0.3，εb=0.7 时NSDI 概率约为εr=0.7，εb=0.3 时NSDI 概率的10 倍。这说明通过调节两脉冲的椭偏率可以在较大范围内控制NSDI 发生的概率。

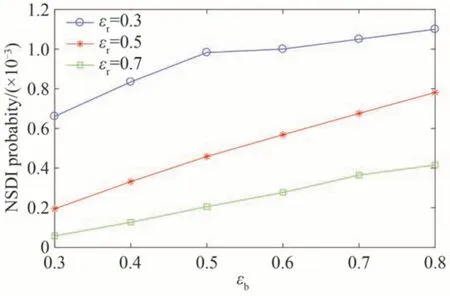
图2 CTEP 场中Ar 原子NSDI 概率对椭偏率的依赖Fig.2 NSDI probability of Ar atoms in CTEP fields as a function of the laser ellipticity

为了分析CTEP 激光场中Ar 原子NSDI 概率椭偏率依赖的原因，进一步检查了电子运动的经典轨迹，并做了统计分析。通常影响NSDI 的发生有两个因素，一个是电子返回的概率，另一个是返回电子与母离子碰撞时它所携带的碰撞能量。如果一个电子电离之后在激光电场的驱动下再次返回母离子附近5 a.u.以内，我们定义该电子返回。图3 是不同椭偏率下CTEP 激光场中电子的返回概率。当固定1 600 nm 脉冲的椭偏率时，电子返回概率随着800 nm 脉冲椭偏率的增大而逐渐增大。当固定800 nm 脉冲的椭偏率时，电子返回概率随着1 600 nm 脉冲椭偏率的增大而逐渐减小。这跟复合电场的波形随激光脉冲椭偏率的变化有关。CTEP 激光场的电场波形由三个波瓣组成，如图1 所示，其中波瓣1 的电场幅值最大，波瓣2 和3 略小。当固定1 600 nm 脉冲椭偏率时，随800 nm 脉冲椭偏率的增加，波瓣2 和3 的电场幅值有所增加，这有利用激光场拉回波瓣1 电离的电子，从而提高电子返回概率。当固定800 nm 脉冲椭偏率时，随1 600 nm 脉冲椭偏率的增加，波瓣2 和3 的电场幅值显著增加，此时y方向较大的电场导致了电子更为严重的横向扩散，所以电子的返回概率减小。

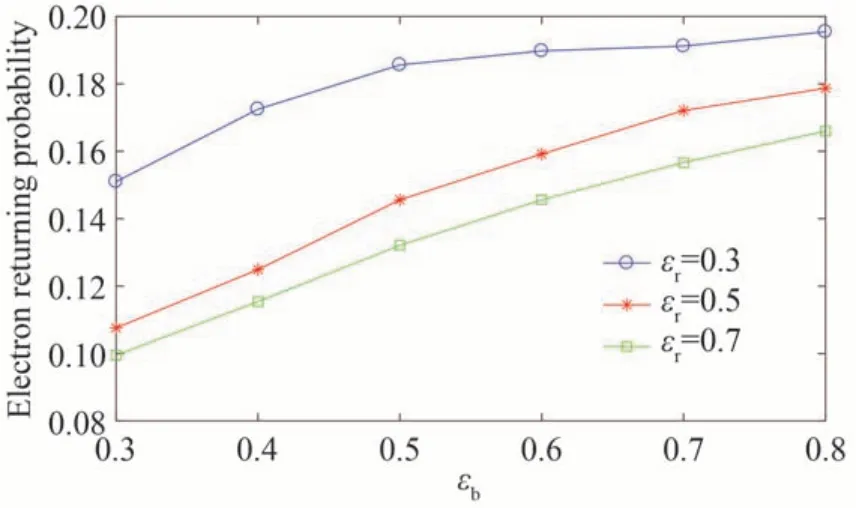
图3 CTEP 场中电子返回概率对椭偏率的依赖Fig.3 Electron returning probability in CTEP fields as a function of the laser ellipticity

进一步定义电子电离后再次返回母离子时，两电子距离最近的时刻为碰撞时间。把该碰撞时间前3 a.u.时刻该返回电子的能量定义为碰撞能量。图4 左图是1 600 nm 脉冲椭偏率为0.7，800 nm 脉冲椭偏率为0.3，0.5 和0.7 时电子碰撞能量的概率分布，从图中可以看出随着800 nm 脉冲椭偏率的增加，电子碰撞能量逐渐增大，越有利于双电离的发生。图4 右图是800 nm 脉冲椭偏率为0.7，1 600 nm 脉冲椭偏率为0.3，0.5 和0.7时电子碰撞能量的概率分布，从图中可以看出随着1 600 nm 脉冲椭偏率的增加，电子碰撞能量逐渐减小，这不利于双电离的发生。

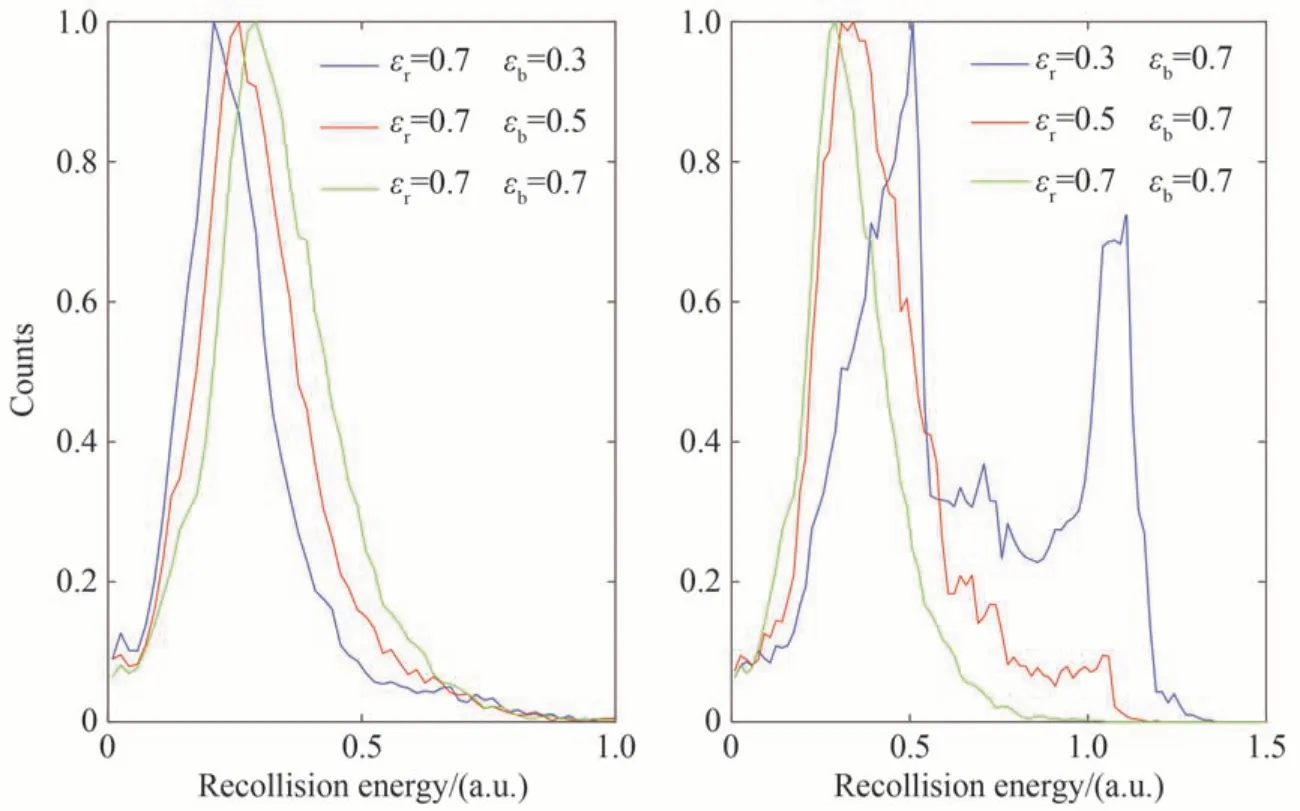
图4 不同椭偏率下NSDI 中电子碰撞能量分布Fig.4 Distributions of the electron recollision energy in NSDI for different ellipticities

通过以上对电子返回概率和碰撞能量的分析可以发现，随着800 nm 脉冲椭偏率的增加，电子的返回概率和碰撞能量都会增大，这两个因素都有利于双电离的发生，所以NSDI 概率随800 nm 椭偏率增加而逐渐增大。而随着1 600 nm 脉冲椭偏率的增加，电子返回概率和碰撞能量都会减小，这对双电离的发生是不利的，导致NSDI 概率随1 600 nm 椭偏率增加而逐渐减小。

根据动量守恒，离子动量可由两电子动量获得，pion=-(pe1+pe2)。图5 是不同椭偏率下Ar2+离子在场平面内的动量分布。首先固定1 600 nm 脉冲的椭偏率，讨论离子动量分布随800 nm 脉冲椭偏率的变化。当εr=0.3（见图5 第1 列）时，Ar2+离子动量分布随εb的增大逐渐由x负半轴向x正半轴移动。当εr=0.5（见图5第2 列）和εr=0.7（见图5 第3 列）时，Ar2+离子动量分布随εb的增大从x轴下方逐渐向x轴上方扩展，最终形成主要分布于x轴两侧的两层分布，并且x轴下方的动量分布始终占比较大。固定800 nm 脉冲的椭偏率，讨论离子动量分布随1 600 nm 脉冲椭偏率的变化。当εb=0.3（见图5 第1 行）时，Ar2+离子动量分布主要在第三象限随εr的增大逐渐下移。当εb=0.5（见图5 第2 行）和εb=0.7（见图5 第3 行）时，Ar2+离子动量分布随εr的增大逐渐变宽，从x轴上逐渐变成分布于x轴两侧，并且x轴下方的动量分布始终占比较大。

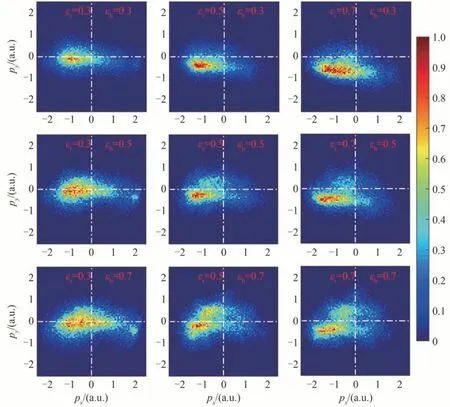
图5 不同椭偏率下Ar2+离子在场平面内的动量分布Fig.5 Momentum distributions of Ar2+ ions in the field plane for different ellipticities

为了解释Ar2+离子动量分布随椭偏率的变化规律，将所有的NSDI 事件分为两类：关联事件和反关联事件。如果两电子最终发射方向的夹角小于90°，则两电子发射到了相同的半球，他们是关联的，该NSDI 称为关联事件。如果两电子最终发射方向的夹角大于90°，则两电子发射到了相反的半球，他们是反关联的，该NSDI 称为反关联事件。图6 和图7 分别给出NSDI 中关联事件和反关联事件的Ar2+离子动量分布。比较图6 和图7 可以发现关联事件中的离子动量较大，即远离原点，而反关联事件中离子动量较小，分布更接近原点。

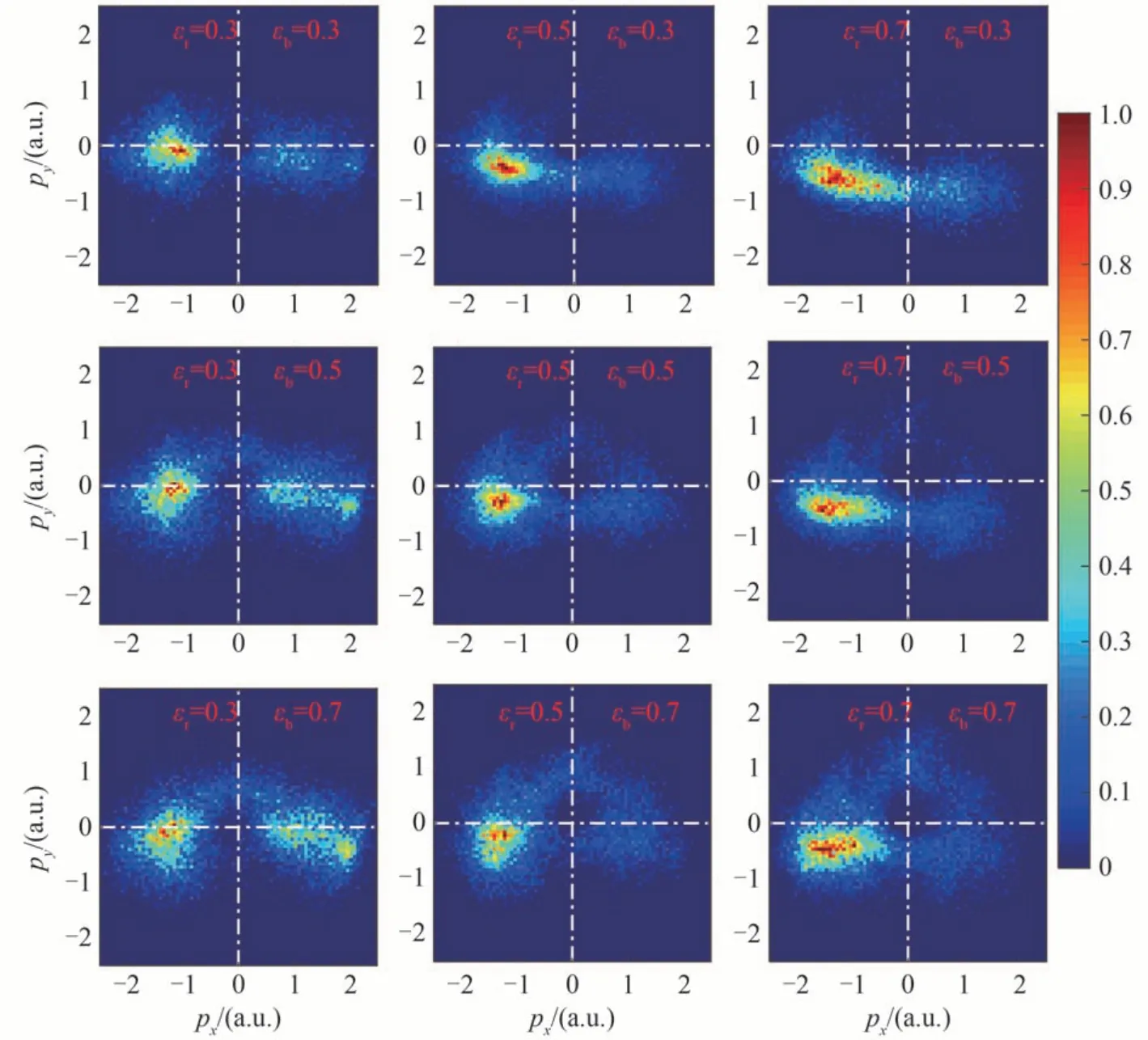
图6 不同椭偏率下NSDI 中关联事件的离子动量分布，其他参数与图5 相同Fig.6 Ion momentum distribution of correlated events in NSDI for different ellipticities，other parameters are the same as Fig.5

图7 不同椭偏率下NSDI 中反关联事件的离子动量分布，其他参数与图5 相同Fig.7 Ion momentum distribution of anti-correlated events in NSDI for different ellipticities，other parameters are the same as Fig.5

图6 和图7 的第1 列是εr为0.3，εb为0.3，0.5 和0.7 时关联事件和反关联事件的离子动量分布。关联事件的离子动量主要分布在两个远离原点的区域，随εb的增大处在x轴正半轴的部分逐渐增多（见图6 第1 列）。而反关联事件的动量分布随εb的增大几乎不变（见图7 第1 列）。所以εr=0.3 时，总的离子动量分布随εb的增大向x轴正向移动。对于εr=0.5（见图6 第2 列）和εr=0.7（见图6 第3 列）的情况，关联事件中Ar2+离子主要分布在第三象限。此时反关联事件随εb的增大逐渐上移，在εb=0.5 时x轴上下分布概率几乎相等（见图7（e）和（f）），在εb=0.7 时离子主要分布在x轴以上的区域（见图7（h）和（i））。由于εr=0.5 和εr=0.7 时，关联事件总是分布在x轴以下，而反关联事件随εb的增大逐渐上移，最终导致总的离子动量分布，随εb的增大在y方向扩展形成一个两层的分布。相似地，如果固定εb为0.7，改变εr，关联事件中离子的动量分布主要处在x轴下方（见图6 第3 行），而反关联事件中的离子从x轴逐渐上移（见图7 第3 行）。导致εb=0.7 时总的离子动量分布随εr的增大逐渐拓宽最终分成两层（见图5 第3 行）。

下文分析离子动量分布随激光椭偏率变化的动力学过程。前面的分析已经表明当εr=0.3 时关联事件中离子动量在x正半轴的分布随着εb的增加而增多导致总的动量分布随εb的增加向x轴正向移动。为了解释这一现象，单独分析了关联事件中第1 个电子和第2 个电子的动量分布（如图8 所示）和关联事件中碰后第1 个电子和第2 个电子最终电离时间的统计分布（如图9 所示）。这里的第1 个电子和第2 个电子是基于碰撞后两电子最终电离的先后顺序而命名。从图8 可以看出，当εr=0.3 时，关联事件中第1 个电子和第2 个电子在x轴负方向的分布都随着εb的增大而增多，这就导致关联事件中离子在x轴正方向的分布都随着εb的增大而增多。为了解释两电子在x轴负方向的分布都随着εb的增大而增多这一现象，分析碰后两电子的最终电离时间。碰撞后第1 个电子电离主要集中在波瓣1 的下降沿，随着εb的增大波瓣1 下降沿电离事件占比下降，波瓣1 上升沿和波瓣3 的电离事件占比增多（见图9 第1 行），根据simple-man 模型，电子电离后的动量主要来自于电场的加速，即电子电离时刻的负矢势。因此，第1 个电子主要分布在x轴正方向，随着εb的增大，第1 个电子在x轴负方向的分布逐渐增多。碰撞后第2 个电子电离主要集中在波瓣1 和波瓣2 的上升沿，并且随着εb的增大波瓣1 电离事件从下降沿占优过渡到上升沿占优（见图9 第2 行），这导致随着εb的增大第2个电子在x轴负方向的分布逐渐增多。

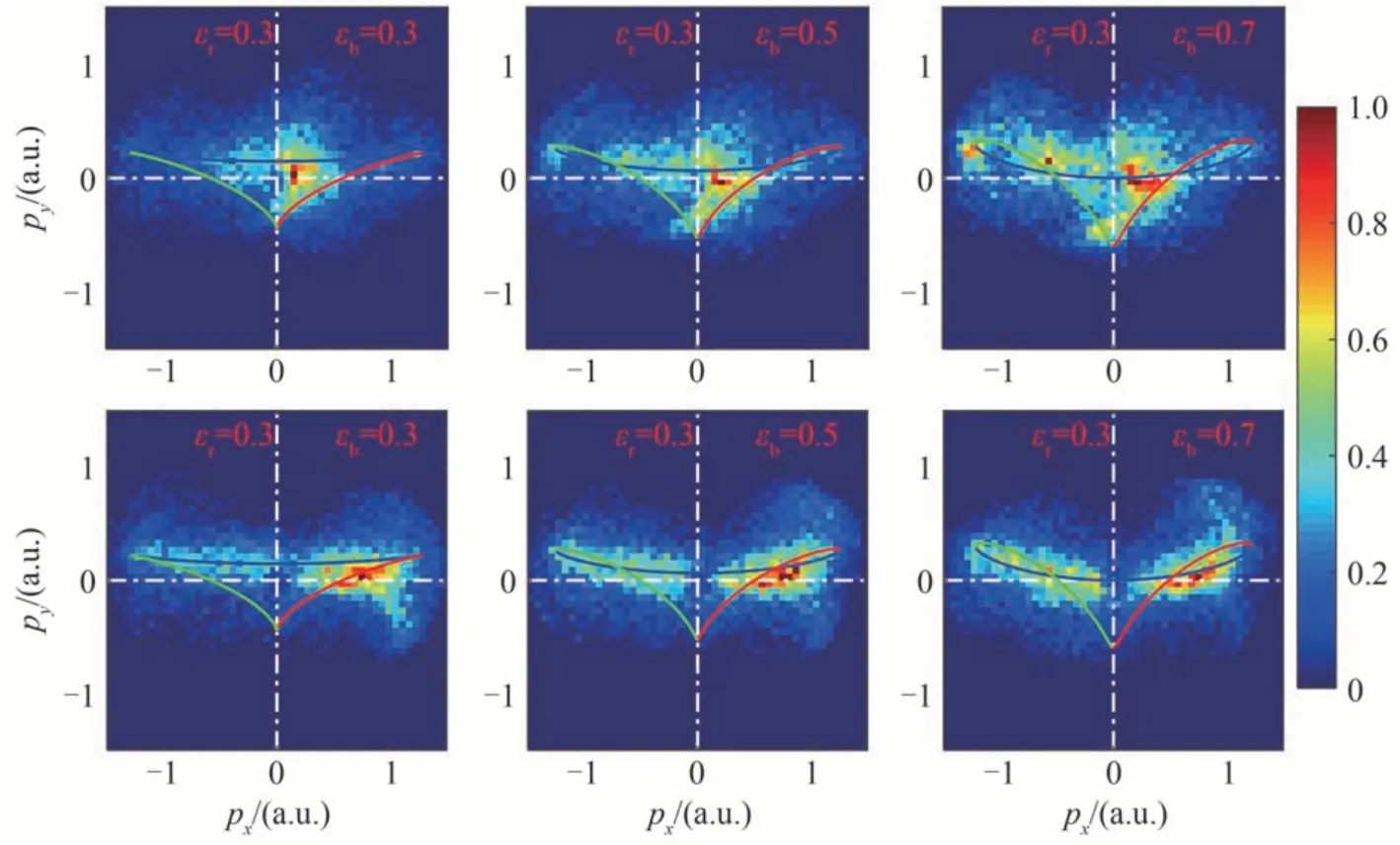
图8 关联事件中第1 个电子（第1 行）和第2 个电子（第2 行）的动量分布，实线为复合场的负失势Fig.8 Momentum distributions of the first electron （the first row） and the second electron （the second row） for correlated events in NSDI，solid lines mark the negative vector potential

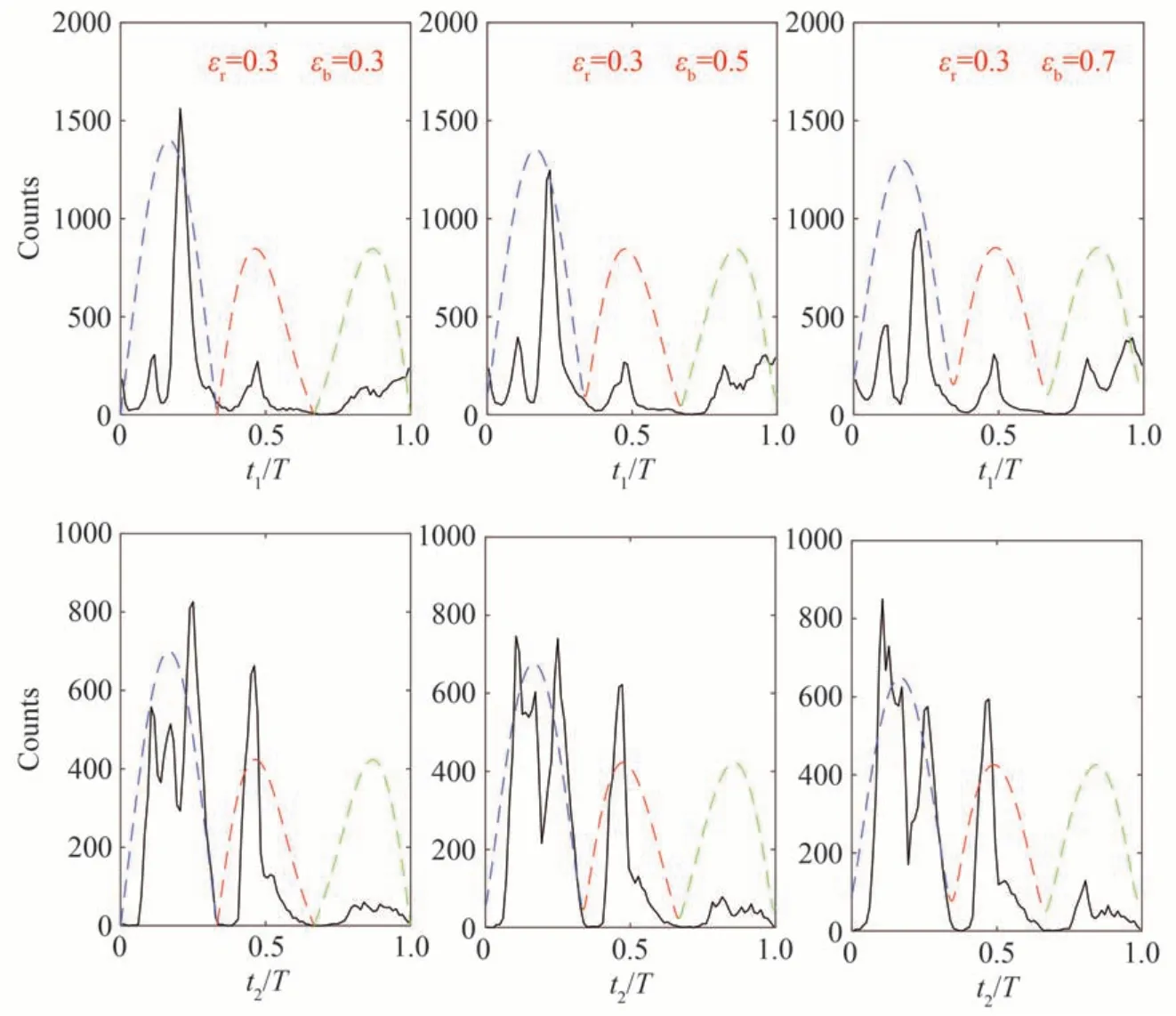
图9 关联事件中碰撞后第1 个电子（第1 行）和第2 个电子（第2 行）的最终电离时间的统计分布Fig.9 Distributions of the final ionization times of the first electron（the first row） and the second electron （the second row） for correlated events in NSDI

从总的动量分布中已经发现，当εr=0.7 时，总的离子动量分布随着εb增大从一个位于x轴下方的集中分布逐渐扩展，最后形成了一个两层结构（见图5 第3 列）。该变化是因为当εb增大时关联事件的离子动量分布保持在x轴下方，而反关联事件的离子动量分布逐渐上移到x轴上方。下文通过电子动量分布和电子电离时间对椭偏率的依赖来解释反关联事件离子动量分布随εb增大而上移的现象。图10 是反关联事件中第1 个电子（第1 行）和第2 个电子（第2 行）的动量分布。当εr=0.7 时，随着εb增大，反关联事件中第1 个电子的动量分布在y正方向的占比减小，在y负方向占比逐渐增多（见图10 第1 行）。当εr=0.7，εb=0.7 时，第1 个电子在y负方向的分布已经多于在y轴正方向的分布。而第2 个电子动量分布在y负方向的占比也略微增加（见图10 第2 行）。这表明第1 个电子和第2 个电子在y方向具有负动量的概率随εb的增大而增加，从而导致了反关联事件中离子动量分布随εb的增大而上移。从电子的电离时间分布上看，随着εb的增大，第1 个电子在波瓣1 电离的概率降低，而从波瓣3 上升沿电离的概率显著增加（见图11 第1 行），这导致该电子有更大的概率在y方向获得一个负方向的加速。而对于第2 个电子，最终电离时间分布随εb的增大变化不大，波瓣2 的下降沿和波瓣3 的上升沿的占比有略微的增加（见图11 第2 行），这导致了第2 个电子动量在y轴负方向的分布仅有略微增加。

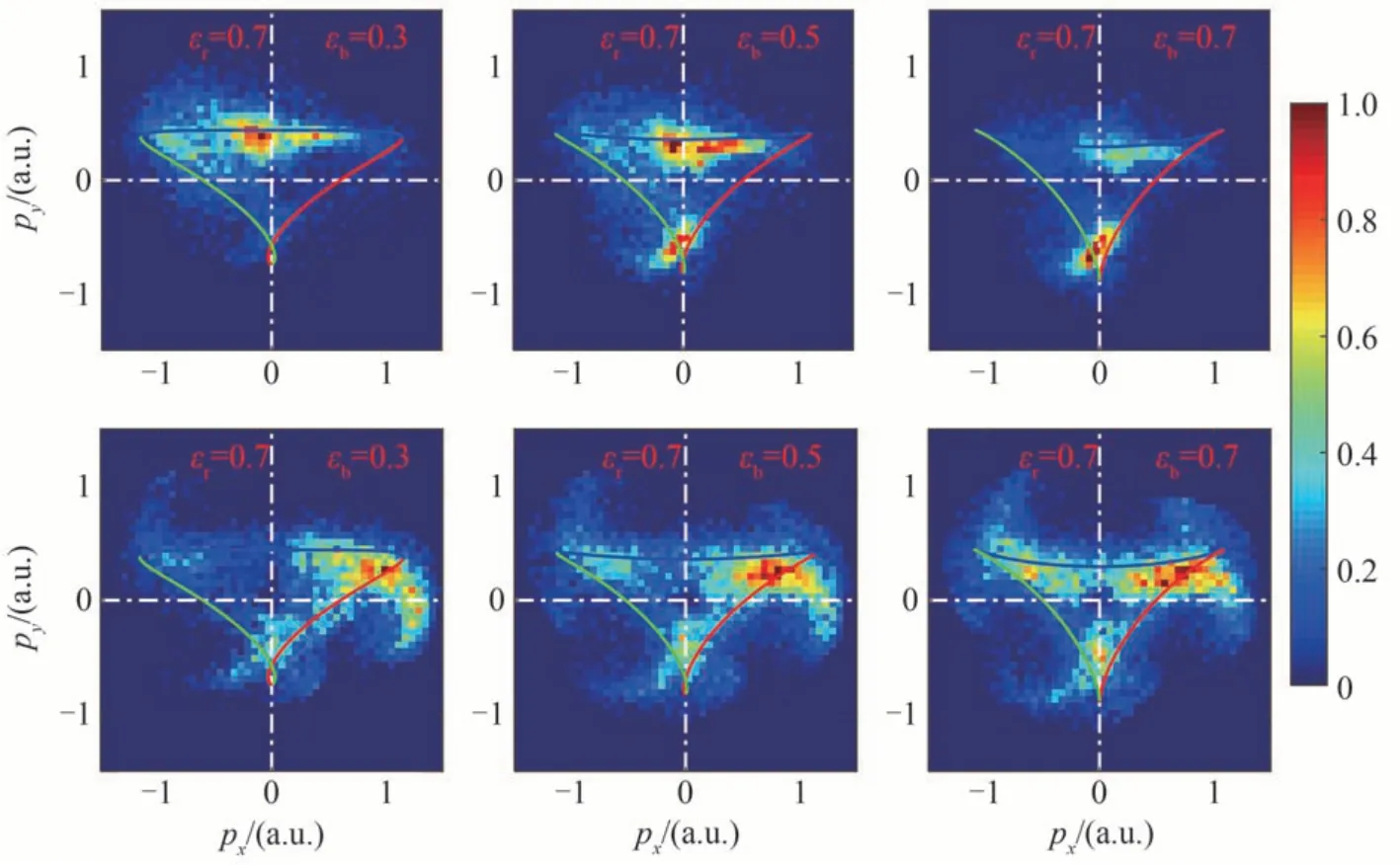
图10 反关联事件中第1 个电子（第1 行）和第2 个电子（第2 行）的动量分布Fig.10 Momentum distributions of the first electron （the first row） and the second electron （the second row） for anti-correlated events in NSDI

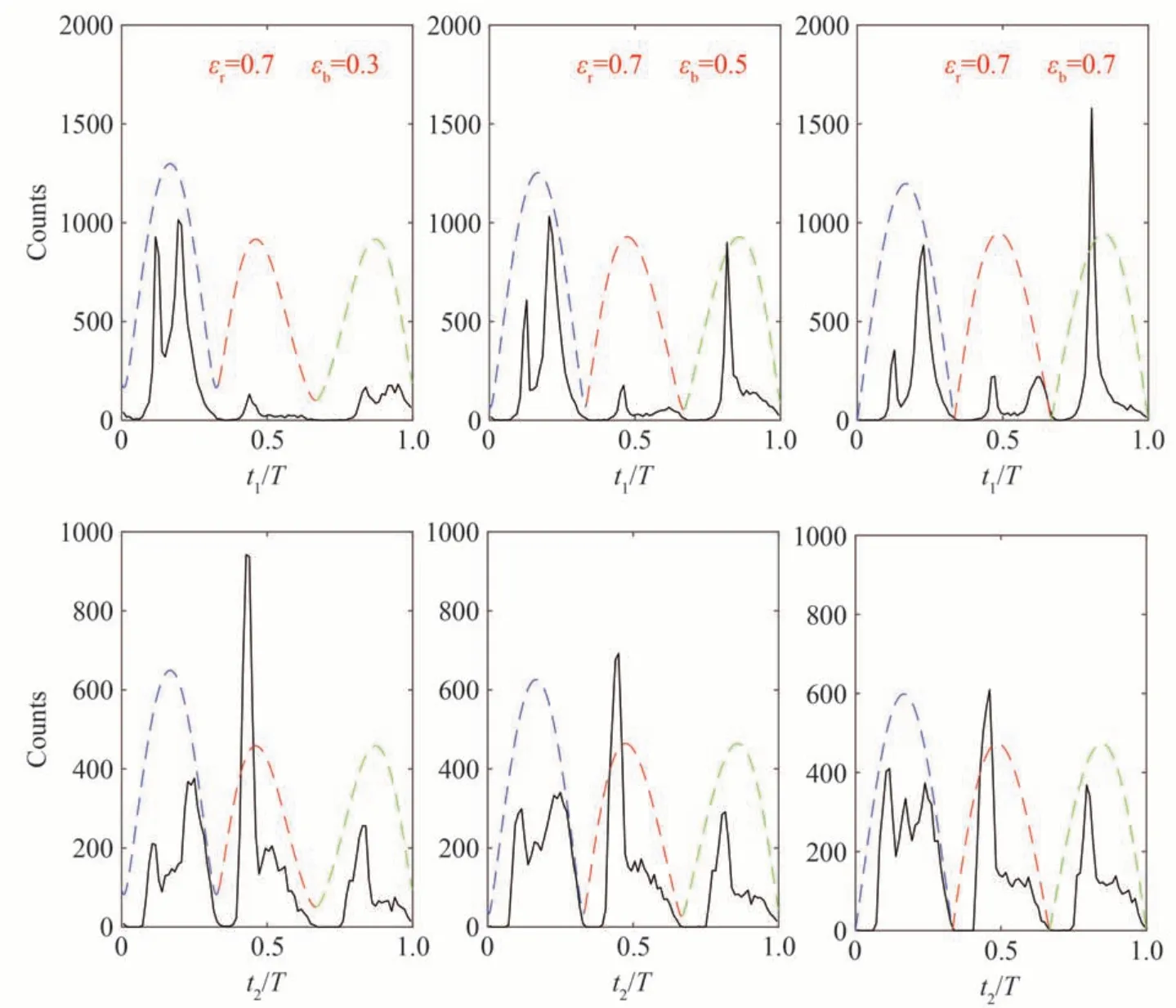
图11 反关联事件中碰撞后第1 个电子（第1 行）和第2 个电子（第2 行）的最终电离时间的统计分布。其他参数与图9 相同Fig.11 Distributions of the final ionization times of the first electron （the first row） and the second electron （the second row） for anti-correlated events in NSDI.Other parameters are the same as Fig.9

当εb=0.7 时，随着εr的增大，反关联事件中离子动量分布的上移导致总的离子动量分布的分层（见图5第3 行）。图12 是反关联事件中第1 个电子（第1 行）和第2 个电子（第2 行）的动量分布。当εb=0.7 时，随着εr增大，反关联事件中第1 个电子的动量分布在y轴正方向的占比减小，在y轴负方向占比逐渐增多（见图12第1 行）。而第2 个电子动量分布在y 轴负方向的占比也逐渐增加（见图12 第2 行）。这表明第1 个电子和第2 个电子在y轴方向具有负动量的概率随εr的增大而增加，从而导致反关联事件中离子动量分布随着εr的增大而上移。从两电子电离时间分析来看，随着εr的增大，第1 个电子在波瓣1 电离的概率降低，而从波瓣3上升沿电离的概率显著增加（见图13 第1 行），这导致该电子有更大的概率在y方向获得一个负方向的加速。而对于第2 个电子，最终电离时间分布随着εr的增大，波瓣2 的下降沿和波瓣3 的上升沿的占比有所的增加（见图13 第2 行），这导致第2 个电子动量在y轴负方向的分布相应地增加。

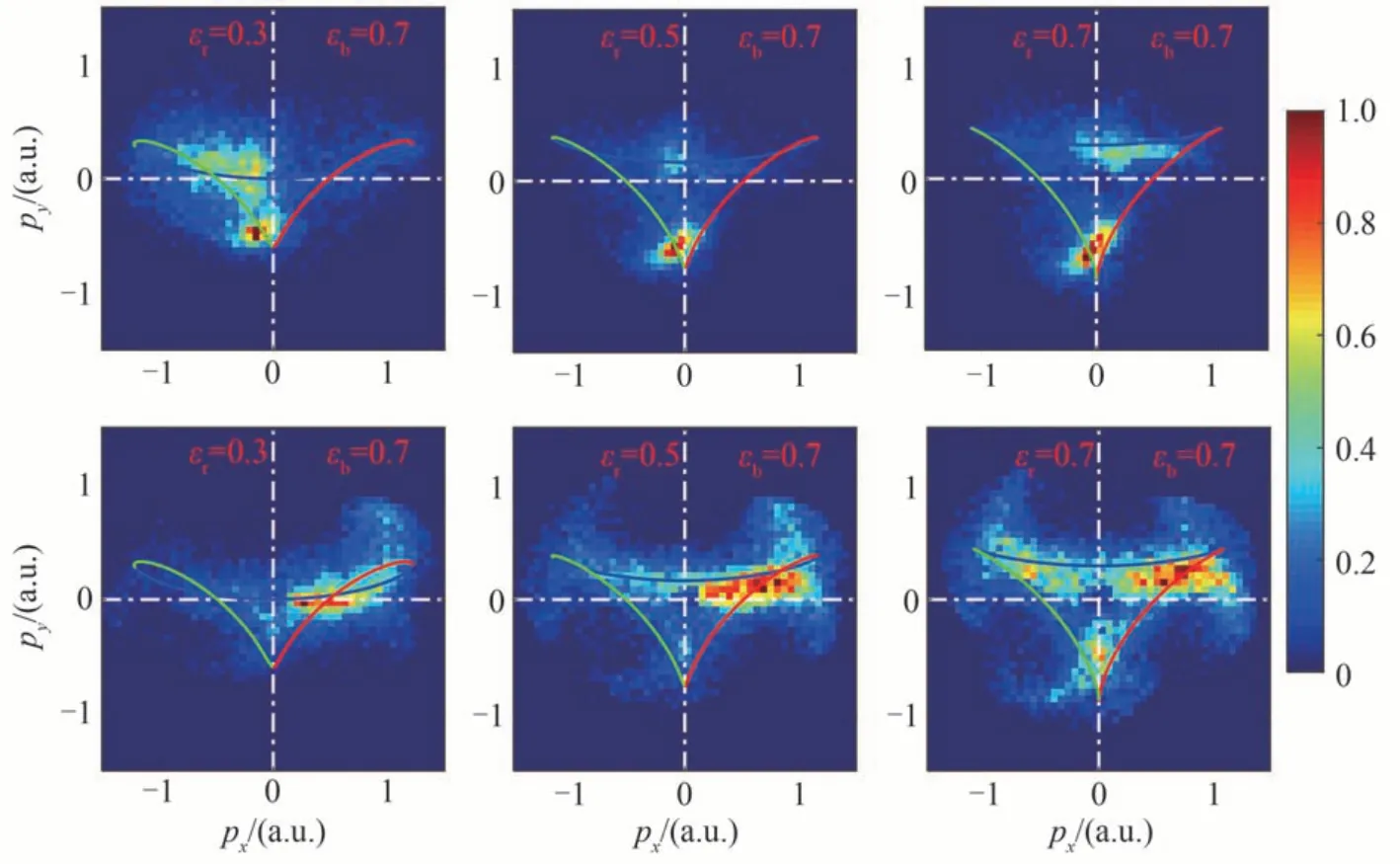
图12 反关联事件中第1 个电子（第1 行）和第2 个电子（第2 行）的动量分布Fig.12 Momentum distributions of the first electron （the first row） and the second electron （the second row） for anti-correlated events in NSDI

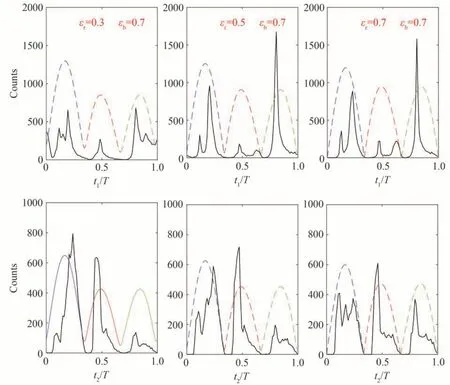
图13 反关联事件中碰撞后第1 个电子（第1 行）和第2 个电子（第2 行）的最终电离时间的统计分布，其他与图9 相同Fig.13 Distributions of the final ionization times of the first electron （the first row） and the second electron （the second row） for anti-correlated events in NSDI，other parameters are the same as Fig.9

3 结论

本文利用三维经典系综模型研究了不同椭偏率的两椭偏脉冲组成的复合光场中Ar 原子的NSDI。数值模拟显示NSDI 概率和离子动量分布都显著的依赖脉冲的椭偏率。NSDI 概率随800 nm 激光场椭偏率增大而增大，随1 600 nm 激光场椭偏率增大而减小。经典轨道分析表明，当固定1 600 nm 激光场椭偏率时，电子的返回概率和碰撞能量随800 nm 激光场椭偏率增大而增大。当固定800 nm 激光场椭偏率时，电子的返回概率和碰撞能量随1 600 nm 激光场椭偏率增大而减小。这是导致NSDI 概率强烈地依赖脉冲椭偏率的原因。当1 600 nm 激光场椭偏率为0.3 时，离子动量分布由x轴负半轴向x轴正半轴移动。并且随着1 600 nm激光场和800 nm 激光场椭偏率的增大，离子动量分布逐渐扩展最终形成一个分布于x轴两侧的两层结构。这些结果表明在双色椭偏场中椭偏率是控制NSDI 产量、离子动量分布和电子返回概率的有效手段。