解题教学要训练学生的“方向感”

徐瑾

［摘  要］ 开展“结构不良”问题的解题教学时，要注重引导学生寻找解题的“方向感”. 特别是一些几何综合题，往往解题方向不够明确，如果不能准确分析、想清解题目标，解题效率往往较为低下. 开展解题教学时可以让优秀学生分享他们是如何获得解题念头、解题方向的，即多让学生说说“怎么想到的”，让学生的思维“可视化”.

［关键词］ 解题教学；方向感；结构不良

从一道“结构不良”几何题的教学说起

所谓结构不良问题，是指问题的初始状态、目标状态、解决问题的模式三种要素中至少有一个没有明确界定的问题. 近年来，不少地区的中考几何综合题往往需要根据条件补全图形，并探索结论，这类问题需要学生具有较强的构图、分析、猜想、验证、排除、确认等综合能力，因而成为一类较有区分度的几何综合题. 下面是笔者在最近的解题教学中对一道几何综合题的教学记录.

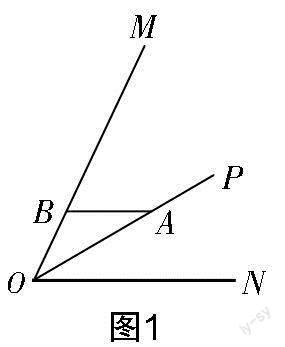
案例1  如图1，已知∠MON=α（0°<α<90°），OP是∠MON的角平分线，A，B分别在OP，OM上，且AB//ON. 以点A为中心，将线段AO旋转到AC处，使点O的对应点C恰好在射线BM上，在射线ON上取一点D，使得∠BAD=180°-α.

（1）依題意补全图形，并证明OC=OD+AD；

教学记录：第（1）问先组织学生补全图形（如图2），然后结合“OP是∠MON的角平分线”“∠BAD=180°-α”可以转化为八年级全等三角形的一个“基本图形”（对角互补四边形），证出AD=AB，进一步代换出AD=AB=OB. 再证△AOD≌△ACB，可得OD=BC，于是OC=OB+BC=AD+OD.

解后回顾：同学们觉得这道题第（2）问的主要难点在哪一步？关键步骤是哪一步？你们有怎样的解题经验值得积累？

教学记录：经过小组交流、全班汇报后，学生认为第（2）问的主要难点是要构造符合题意的图形，如果图形不准确会影响后续分析；关键步骤是猜想出α为45°（即△COD是等腰直角三角形）；值得分享的经验是善于猜想几个特殊锐角，并进行快速验证、排除或确认.

教后反思：可以发现，学生猜想一些特殊锐角的经验是问题获得突破的关键步骤，而猜想特殊锐角就是明确、明晰解题方向，这样才能进一步构造出准确的图形，直至顺利解答. 这说明在解题进程中，训练必要的“题感”、明晰解题“方向感”是教师应向学生传递和训练的一种高阶思维能力.

解题教学重视“方向感”训练的进一步思考

第一，几何入门阶段就要开始训练“方向感”

学生解决几何综合题时，解题障碍主要出现在构图分析、思路突破、规范表达这三个方面，特别是有些几何题感觉无从下手、“方向不明”（这里主要是指不知向什么方向前进，而不是题目是否给出了“明确设问”）. 根据教学经验，有些学生在面对较难的几何综合题时，如果启发他们某个关键图形或提醒某个特殊位置，他们往往就能快速获得思路突破. 究其原因，教师在几何入门阶段就要重视训练学生的“方向感”［1］，举例来说，在同一平面内，两条直线的位置有相交与平行，当两条直线相交时，垂直相交就是一种特殊的位置关系，它所对应的是相交所成的4个角都是直角. 那么组织垂直的概念学习时，就要让学生能从位置关系与数量关系对应的“正反”角度来深刻理解，这样将来遇到一些复杂的几何图形中出现垂直或90°的信息时就要能向90°或垂直的方向思考，从而发现这些特殊的位置或数量关系，有利于思路的获得. 顺便指出，当学生新遇到一个几何对象时，教师不但要帮助学生归纳概括出这个几何对象的概念（即图形的定义），而且板书概念时，图形的定义“旁边”要有一个“标准图形”（在小结阶段还可以给出这个概念的“非标准图形”或变式图形），接着还要板书几何符号语言，对于定义的符号语言，比如角平分线的符号语言，还要“双向”书写，如由角平分线知角的数量关系，反过来，由角的等量关系可得角平分线.

第二，重视特殊图形的研究可强化“方向感”

初中阶段几何图形的学习和研究多是从“一般到特殊”的“由大到小”的学习顺序. 比如先学习三角形，然后再研究特殊的三角形；再如先学习等腰三角形，再研究等边三角形；又如先学习平行四边形，再研究特殊的平行四边形. 研究特殊图形时，要引导学生辨明图形的“特殊之处”，而且要从多个角度（定义、性质与判定）进行理解，并善于在图形语言、文字语言、符号语言之间灵活切换与转译. 对特殊图形的深刻理解能帮助学生在遇到“残缺不全”的图形问题时，想到通过添加必要的辅助线将“残缺不全”的图形转化为特殊图形，借助特殊图形的性质获得问题突破，这也是帮助学生获得更好的解题“方向感”的有效方式. 比如，当一个图形问题中出现等腰直角三角形的条件时，若思路限于等腰直角三角形难以打开局面、陷入僵局，便可以考虑将等腰直角三角形“补全”为正方形，在正方形的背景下继续思考，有时往往能获得进展.

第三，解题“方向感”就是让目标得到明晰

根据波利亚解题理论，解题主要分为“我在哪儿（出发点）”“我到哪儿去（前进方向）”“如何到达（解题路径）”，本文主要关注的是“前进方向”. 有些问题的求解目标（结论）没有明确，比如“探究图形中有几对角相等，几组三角形全等”或“这个方程有没有实数根”或“该函数图象是否存在某个点满足……”等，这些设问都没有明确的方向，需要解题者结合题意分析出它们的解题目标.比如，探究一元二次方程有没有实数根的目标可能是分析该方程的根的判别式；再如，要分析图形中是否存在全等三角形，关键是分析图形中有哪些三角形中的边、角有对应相等的可能. 此外，还有不少问题的设问看似明确，比如求某条边长，关键或目标却是要证明全等三角形；再如，有些求某两条线段的乘积，关键却是找到这两条线段所在的三角形并证明它们相似. 顺便提及，命题设问中有所谓的“等价结论”，在解题教学中善于向学生传递并分享“等价结论”，也是训练学生解题“方向感”的有效方式.

第四，重视“方向感”就是要加强解题监控

笔者开展解题教学的经验表明，解题水平高的学生往往有着很强的目标意识（即方向感很好），他们总能找准攻克的方向，即使出现解题方向的偏离，也能很快“折返”重新出发，所以解题速度快、弯路少. 而有些解题能力相对较弱的学生，其常常表现为走一步算一步，从已知条件出发，漫无目的，甚至在陷入繁难运算之后仍然不知道要“掉头折返”，僵持固执，浪费时间. 所以，要让更多的学生知晓解题目标或方向是先于具体运算或思路贯通之前要优先考虑的［2］. 比如，有些含有多个参数的代数问题，其基本方向应该是优先“消参”（消元），然后才可能出现较为明确的解题路径；又如，初学因式分解时，优先考虑提公因式法也是重要的变形方向；再如，七年级初学有理数运算时，向学生传递优先确定符号，也是重要的解题方向. 可见，教师在不同年级、不同阶段的解题教学中都要向学生分享“方向感”. 正如那句俗语“方向如果错了，越努力离目标越远”一样，重视“方向感”就是要加强解题监控.

写在后面

解题教学在初中阶段占有很大比例，教师如何修炼解题教学基本功是一个很大的课题. 笔者关于解题教学要训练学生的“方向感”的心得体会只是盲人摸象，还有待进一步实践研究和反思总结. 笔者期待更多同行能在解题教学这个领域分享成功的案例和经验，以促进解题教学的研究不断走向深入.

参考文献：

［1］郑毓信. 中学数学解题教学之我见（下）［J］. 中学数学月刊，2020（11）：1-4.

［2］刘东升. 学测命题要重视“关键题”的教学导向——有感于一道九年级“纠错题”［J］. 教育研究与评论（中学教育教学），2021（04）：94-96.