多策略融合的黄金正弦樽海鞘群算法
2023-12-16丁美芳吴克晴肖鹏
丁美芳 吴克晴 肖鹏
樽海鞘群算法;选择反向学习;精英均值;黄金正弦算法
0 引言
优化问题在人工智能领域和现实生活中普遍存在,一直以来备受学者关注.元启发式优化算法机制灵活,仅需改变部分参数或搜索策略便可运用于各类优化问题,兼容性很高.近几十年来,学者们提出了许多元启发式优化算法,例如粒子群优化算法(Particle Swarm Optimization,PSO)[1]、鲸鱼优化算法(Whale Optimization Algorithm,WOA)[2]、郊狼优化算法(Coyote Optimization Algorithm,COA)[3]、哈里斯鹰优化算法(Harris Hawks Optimization,HHO)[4]、黑猩猩优化算法(Chimp Optimization Algorithm,ChOA)[5]等.
樽海鞘群算法(Salp Swarm Algorithm,SSA)是一种新型元启发式优化算法,由Mirjalili等[6]于2017年首次提出.相较于其他群智能优化算法,樽海鞘群算法具有结构简单、参数少、易于实现等优点.自提出以来,该算法被广泛应用于无源时差定位[7]、PMSM参数辨识[8]、图像分割[9]、特征选择[10]、训练神经网络[11]、网页排名[12]等多个领域.
然而,同其他群智能优化算法一样,樽海鞘群算法仍存在收敛速度慢、容易陷入局部最优[13]等问题.为此,国内外学者做了一些改进:文献[13]采用折射反向学习产生动态候选解,同时在跟随者阶段引入非线性递减的自适应控制因子,提升算法开采能力;文献[14]将Sigmoid函数的扰动参数应用于领导者位置更新的概率参数中,增强种群多样性,提升算法的勘探能力;文献[15]在领导者位置更新阶段引入疯狂算子,并通过一定概率随机扰动食物源的位置,从而维持领导者个体的多样性;文献[16]在领导者位置更新阶段引入控制搜索范围的非线性衰减因子,有利于算法在前期跳出局部最优;文献[17]采用平方指数和高斯模型相结合的方法,将平方指数策略引入领导者位置更新,增强了算法的收敛性能;文献[18] 提出一种基于惯性权重和领导者-跟随者自适应调节方法,实现了对全局搜索和局部搜索的优化,从而大大提高了寻优精度.
上述改进算法虽然都在一定程度上改善了基本SSA的性能,但是对一些复杂度较高、规模较大的问题,算法的收敛速度和稳定性仍有改进的空间.因此,本文提出一种多策略融合的黄金正弦樽海鞘群算法(Golden sine Salp Swarm Algorithm with Multi-strategy,MGSSA).首先,在初始阶段引入选择反向学习策略,丰富种群多样性,改善初始解的质量.其次,将最优个体和精英均值个体引入跟随者位置更新阶段,增强整个种群之间的信息交互能力,使跟随者位置在迭代初期更侧重于跟随全局最优个体,加快收敛速度,在迭代后期更侧重于相邻个体之间的交流,提升局部开采能力.该策略很好地平衡了算法的全局勘探和局部开采能力.最后,融合黄金正弦算子和判定参数对个体位置进行变异,强化算法跳出局部极值的能力.理论分析证明了本文提出的算法并未增加算法的时间复杂度,同时选取14个基准测试函数进行数值比较实验,结果表明,在SSA中融合上述改进策略提升了SSA的收敛精度和稳定性,从而提高了算法性能.将MGSSA应用于拉压弹簧工程问题,取得了较好的结果.
1 樽海鞘群算法
樽海鞘群算法[6]模拟了自然界中樽海鞘群以链式结构进行捕食的过程.该算法分为领导者位置更新和跟随者位置更新两个部分.算法将每一代的最优个体设为领导者,其余个体均为跟随者.
与其他群智能优化算法类似,在求解问题时,樽海鞘群个体在D×N的空间中展开搜索,其中,D为给定问题的变量数,N为种群数量.这样,樽海鞘群个体位置就被存储在一个称为X的二维矩阵中,空间中樽海鞘群的位置用Xn=[Xn1,Xn2,…,XnD]T表示,在搜索空间中有一个名为F的食物源位置用Fn=[Fn1,Fn2,…,FnD]T表示.
(1)

(2)
其中:t为当前迭代次数;T为最大迭代次数.
在基本的樽海鞘群算法中,每个跟随者更新的位置只与其历史位置以及前一名个体的位置有关.其位置更新公式如下:
(3)

2 改进樽海鞘群算法(MGSSA)
在基本SSA中,每次迭代通常取上一次迭代的最优个体作为整个种群的领导者,其余个体均为跟随者.由于领导者数目单一,种群进化方向趋同,整个算法的全局勘探能力较弱,在求解复杂问题时,容易陷入局部最优.同时,基本SSA中跟随者的位置更新仅与和它相邻的个体位置有关,这在一定程度上限制了算法的收敛速度以及搜索方向.为改善基本SSA算法存在的问题,本文提出以下改进策略:
1)提出一种选择反向学习策略,提高种群质量,同时协助种群在搜索后期跳出局部最优;
2)针对算法收敛速度慢的问题,在跟随者位置更新阶段引入最优个体和精英均值个体引导,吸收更多优质个体的有利信息;
3)根据不同的变异概率,选取不同的黄金正弦变异策略,使算法在前期以较大概率向群体均值方向前进,加快算法寻优速度,后期侧重挑选随机个体进行周边搜索,便于跳出局部最优.
2.1 选择反向学习策略
反向学习(Opposition-Based Learning,OBL)的基本概念最初是由Tizhoosh[19]提出的,其主要思想是通过同时比较当前位置的目标函数值及其相反位置的目标函数值,保留两者中的适应度值更优的点,从而扩大搜索范围.目前已经有许多研究将反向学习策略融入到智能优化算法中,算法的求解性能均有所增强[20].
选择反向学习(Selective Opposition-Based Learning,SOBL)是一种由反向学习启发的新型算法改进策略,其主要思想是通过将两个体间各维度位置的距离与给定的阈值进行比较,在远距离维数大于近距离维数的情况下,选择距离大于阈值的维度进行反向学习,从而提高个体解的质量.SOBL近年来被应用于改进灰狼优化算法[21],且经过实验证实对算法性能的改善有正向促进作用.本文将其应用于樽海鞘群算法改善搜索性能.SOBL基本原理如图1所示.

图1 SOBL原理示意图Fig.1 Principle diagram of SOBL
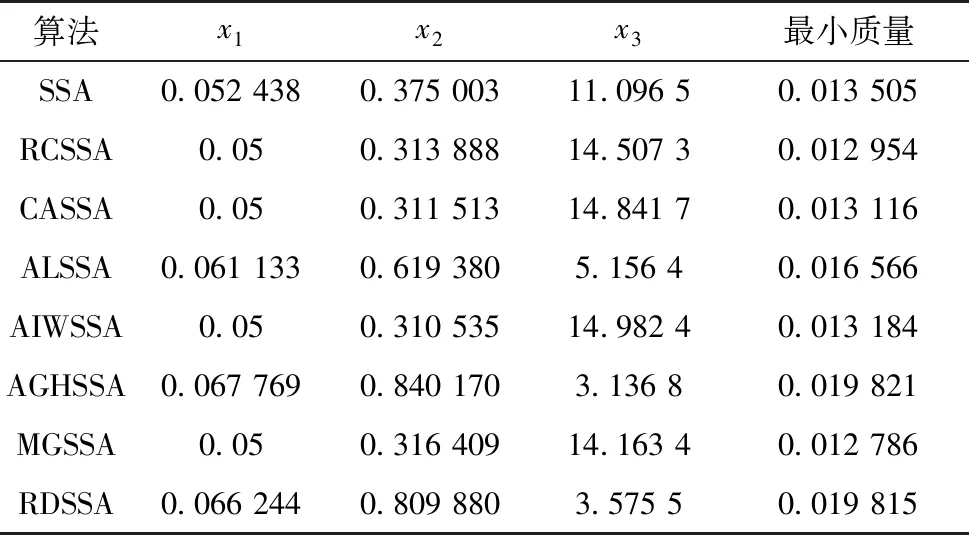
在图1中,假设有一个三维空间,(a,b,c)是食物源的位置,五角星的位置为问题最优解的位置,(a′,b′,c′)是(a,b,c)的完全相反点.最优解位置与(a,b,c)和(a′,b′,c′)的距离分别为d1和d3.同时假设(a′,b′,c)是(a,b,c)仅前二维相反的点(选择性相反),其与解的距离为d2.从图1中可以看出,d2 在介绍选择反向的具体实现步骤前,需要先了解斯皮尔曼相关系数. 2.1.1 斯皮尔曼系数 斯皮尔曼相关性分析是一种查找两个序列之间的统计相关性的方法(此处为两个寻优个体的位置).假设有两个序列k1,k2,k3,…,kn和l1,l2,l3,…,ln,令di=ki-li,i=1,2,…,n,则两者间的斯皮尔曼相关系数[22]为 (4) 其中,n为序列维度.在每次迭代之后,根据食物源的位置计算每个个体的斯皮尔曼系数.若相关系数为负,则表明该个体位置与食物源位置相反,继续朝该方向开采获得更有益信息的概率相对较小,进行反向学习可以加大寻找到有益信息的概率;反之,若相关系数为正,则表明该个体位置与食物源位置一致,继续朝该方向搜索有利于挖掘更多有益信息,因而无需进行反向学习.总体而言,使用斯皮尔曼系数有助于选择需要反向学习的个体,减少不必要的个体反向操作. 2.1.2 选择反向学习机制 对每个斯皮尔曼系数小于零的个体,给定一个阈值a,其计算公式如下: (5) 其中:t为算法当前迭代次数;T为算法最大迭代次数.阈值a是随迭代次数线性减少的,该值确定该个体位置是否接近食物源.对于当前个体和食物源的每个维度j,使用式(6)计算它们之间的差值: D(j)=|X(j)-F(j)|, (6) 其中:X(j)为当前个体第j维位置;F(j)为食物源第j维位置.如果差值D(j)大于阈值a,则差值较大的维数gno将增加.设总维数为n.若(n-gno) (7) 选择反向学习与传统反向学习相比,优点在于:用斯皮尔曼系数筛选与食物源位置相反的个体进行反向,保留了相对优质个体的同时减少计算量,通过阈值决定反向的维度,细化反向的方向,使个体搜索更靠近最优方向. 在基本的樽海鞘群算法中,除了一个领导者之外,其余的都是跟随者.跟随者的搜索方向仅和自身位置及与它相邻的个体位置有关,这在一定程度上影响了算法的收敛速度及搜索方向.为了使跟随者能更快地搜索到有益信息,本文设计了一种受种群最优个体和精英群均值个体影响的跟随者搜索策略. 文献[23]提出一种自适应领导者结构,本文在此基础上提出由1自适应增加到N/2的线性精英群.每次迭代的精英种群数量如下: m=「(t/T)×(N/2)⎤, (8) (9) 引入种群最优个体和精英均值个体位置更新公式如下: (10) 其中,c1更新参照式(2). 在迭代初期,个体搜索比较盲目,此时跟随者的位置更新融合了种群最优个体和精英群均值个体位置,可以使跟随者在前期开发出更多更好的解.而在算法后期,随着参数c1的逐渐减小,精英个体对跟随者的影响也会更小,而且此时种群搜索范围也更小,即使是跟随者,蕴含的有益信息量也很大,此时削弱精英个体的影响,对于整个算法而言,可以拓宽算法的勘探能力,这种机制有助于算法在迭代后期跳出局部最优. 黄金正弦算法是2017年由Tanyildizi等[24]提出的新型智能算法.受正弦函数启发,黄金正弦算法取黄金分割数使粒子在更优的搜索范围进行寻优,加快了算法的收敛速度.选取的黄金正弦算子具体公式如下: Xi(t+1)=Xi(t)|sinR1|+ R2sin(R1)|aXbest-bXi(t)|, (11) 其中:R1为0到2π的随机数,决定个体i下一代位置更新的移动步长;R2为0到π的随机数,决定个体i下次更新的方向;a和b为黄金分割系数,影响着粒子的搜索空间,对搜索空间进行了一个更优的选择,引领粒子趋近于更优值.计算公式如下: a=-π(1-τ)+πτ, b=-πτ+π(1-τ), (12) 本文利用黄金正弦算子的优势,对樽海鞘群算法个体进行变异,打开更优的搜索空间,向更优解靠拢.为避免陷入局部最优,分概率采用均值策略和随机策略选取粒子进行变异操作.具体公式如下: (13) 为了防止过早收敛并达到全局最优,需要在勘探和开采之间保持良好的平衡,这种平衡就是通过参数p实现的.在算法迭代前期,种群相对分散,精英均值个体蕴含较多有利信息,在周边搜寻可以加快收敛速度,而此时c1较大,也使得在精英均值个体周围搜索的概率更大.随着种群不断进化,后期p>c1/2的概率更大,算法更多在随机选择的个体周围进行搜索,有利于跳出局部最优. 在进行黄金正弦变异后,将变异后的个体适应度值与原种群对应个体适应度值对比,保留适应度值小的,更新其位置. MGSSA算法伪代码如下: 1)设置种群规模N,维数D,最大迭代次数T 2)随机初始化种群{xi,i=1,2,…,N} 3)计算初代种群适应度并排序,记录当前最优个体位置FoodPosition 4)Whilet≤T 5)根据式(5)更新阈值a 6)筛选种群进行选择反向学习,计算适应度,比较学习后个体与之前的个体的适应度值大小,选更小的个体作为新的位置 7)fori=1 toN 8)if (i==1) 9)根据式(1)更新领导者个体位置 10)else 11)根据式(10)更新跟随者位置 12)end 13)更新变异概率p 14)ifp≤c1/2 15)根据式(13)对每个个体xi位置进行变异 16)else 17)根据式(13)对每个个体xi位置进行变异 18)end 19)end 20)计算每个个体的适应度值,更新FoodPosition 21)end while 22)输出最优位置FoodPosition及其适应度值FoodFitness 在基本的SSA中,假设樽海鞘群种群规模为N,解空间为n维,求解目标函数所需的执行时间为f(n).根据文献[18],SSA算法的时间复杂度为 T(n)=O(n+f(n)). 在MGSSA算法中,参数初始化执行时间η0,每维生成随机数时间η1,求解目标函数执行时间f(n)对适应度值排序时间为η2,则初始化阶段时间复杂度为 T1=O(η0+N(nη1+f(n)+η2)= O(n+f(n)). 进行选择反向学习阶段,根据式(5)计算阈值a时间为η3,根据式(6)计算每个跟随者与食物源之间的距离所需时间为η4,根据式(4)根计算对应斯皮尔曼系数时间为η5,假设斯皮尔曼系数为负的个体数为n0(n0 T2=O(η3+N(nη4+η5)+n0nη6)=O(n), 在领导者位置更新阶段时间复杂度为 T3=O(n). 在跟随者位置更新阶段,跟随者数目为N-1,设由式(10)对跟随者每一维进行更新的时间为η7,则这一阶段的时间复杂度为 T4=O((N-1)nη7)=O(n). 在黄金正弦算子变异阶段,生成变异概率p时间为η8,根据式(13)对每个个体变异的时间为η9,则这一阶段时间复杂度为 T5=O(η8+Nnη9)=O(n). 在边界处理和更新食物源位置阶段,时间复杂度与基本SSA一致,为 T6=O(n+f(n)). 综上可得MGSSA算法的总时间复杂度为 T(n)=T1+T(T2+T3+T4+T5+T6)= O(n+f(n)). 由此可知,MGSSA与基本SSA相比,并未增加时间复杂度. 为了评估 MGSSA的性能,实验从文献[25]中选取了14个基准测试函数,包括7个单峰函数f1~f7和7个多峰函数f8~f14,在表1中列出了各函数的名称及其他相关属性.将MGSSA与14种算法进行比较,包括3种单策略改进算法、6种最近几年提出的SSA改进算法和5种群智能优化算法.最后将改进算法应用于工程约束优化问题探究其求解效果.为了验证数值的有效性,对14个基准函数运行30次的MGSSA和其他比较算法的结果进行非参数Wilcoxon秩和检验,根据每次运行获得的均值,对实验结果进行统计分析,帮助判断各算法与最优算法之间是否具有显著性差异,从而更好地评判算法的性能.其中显著性水平校正为0.05,将均值最小的算法视为最优算法,记作NA.若均值相同,则认为标准差越小的算法越好.若p值小于0.05,则认为该算法与最优算法存在显著性差异,若大于0.05,则该算法与最优算法无显著性差异.符号“+”表示提出的算法得到的结果优于比较算法,而 “-”表示提出的算法得到的结果相较于比较算法更差,符号“=”表明彼此间没有显著差异.因此表中 “+/=/-”行给出算法在14个基准函数上优/等/劣的个数.所有实验都是在操作系统为Windows 11的PC机上用Matlab2019a软件实现的,PC机配置AMD R5 3500U处理器,主频 2.10 GHz CPU,内存8 GB. 表1 基准测试函数 为探究不同策略对算法改进的影响程度,对仅添加精英均值个体策略的改进算法ESSA,仅融合黄金正弦变异的算法GSSA和加入选择反向学习策略的算法SOSSA与 MGSSA进行对比实验. 4种算法独立运行30次的统计结果如表2所示,部分函数收敛曲线如图2所示.可以看出,在14个函数中,ESSA、GSSA和MGSSA分别在3、9、14个函数中寻到了最优,而SOSSA在14个函数的求解效果均差于其他3种算法.这表明黄金正弦融合策略与精英均值个体对标准SSA的改进起较大作用,选择反向学习策略对标准SSA的改进帮助较弱.通过图2也可以发现,与标准SSA相比,选择反向学习策略在求解单峰函数时,虽然收敛效果方面的提升并不明显,但在一定程度上改善了算法的求解精度.因此,将其用于算法开始,改善种群多样性十分合适.同时可以看出在函数f12收敛曲线中,GSSA在200代左右就陷入了局部停滞,而MGSSA在800代左右仍然可以跳出局部最优,进一步寻找更优解,其搜索性能明显更佳.综合表2数据,MGSSA在14个函数上表现均优其他3种单策略改进算法,这表明将3种策略融合求解问题可以有效提升算法的求解性能. 表2 不同改进策略实验测试结果 图2 不同策略函数收敛曲线Fig.2 Convergence curves of different strategy functions 实验选取5个群智能算法进行比较,分别为SSA[6]、GoldSA[24]、HHO[4]、WOA[2]、ChOA[5],为保证实验的公平性,相应算法的参数根据对应参考文献进行设置.本文的MGSSA与这5种算法比较的结果数据如表3所示. 表3 其他群智能算法比较实验结果 根据表3的结果,MGSSA可以在7个单峰函数中找到6个函数的精确最优值,表明该算法具有较强的鲁棒性和较高的收敛精度.对于唯一一个未寻到精确最优值的函数f5,其最优值、均值和标准差均优于其他5种算法.因此,MGSSA在求解单峰函数时具有良好的稳定性和较强的开采能力.对于7个多峰函数,MGSSA寻到了4个精确最优值,在另外3个函数上也找到了接近全局最优值,表明MGSSA有较强的摆脱局部最优的能力.对于函数f8和函数f14,GoldSA和HHO均寻到相似和相同最优值,但MGSSA的均值和标准差优于GoldSA和HHO,表明MGSSA的稳定性更强.从优/等/劣的结果中也可以看出,MGSSA分别在14、5、11、13、14个函数上结果优于SSA、GoldSA、HHO、WOA、ChOA,在6种算法中总体求解性能最佳.结果表明MGSSA在求解单峰函数中有较强的开采能力,在求解多峰函数时可以有效避免局部最优,有较强的勘探能力.图3是各算法部分函数收敛曲线,可以更直观地观察算法的求解性能. 图3 群智能优化算法函数收敛曲线Fig.3 Convergence curves of functions for swarm intelligence optimization algorithms MGSSA可以有更好的测试结果,主要是均值个体策略优化了跟随者的搜索方向,从而改善算法的开采能力,在算法后期又有黄金正弦扰动帮助其跳出局部最优.SOBL优化了整体种群位置,加快种群的收敛速度同时也改善解的质量. 为进一步测试MGSSA的性能,使用6种其他的SSA改进算法与MGSSA对比,包括CASSA[15]、RDSSA[16]、RCSSA[13]、 ALSSA[18]、AIWSSA[26]和AGHSSA[27].所有算法相关参数均按相应参考文献设置,在14个基准函数上进行测试,各算法独立运行30次,在α=0.05显著水平下通过Wilcoxon秩和检验获得的实验结果如表4所示. 表4 SSA改进算法实验测试结果 从表4可以看出:在14个基准测试函数中,MGSSA在6个单峰函数和7个多峰函数上具有最佳的平均值;针对未寻到精确最优值的函数f5,也优于除RCSSA以外的5个改进算法,总体求解效果最优.同时可以观察到,与同样融合了黄金正弦算法的AGHSSA相比,MGSSA在1个单峰函数(f5)和3个多峰函数(f8、f12、f14)上寻到了更优,而对比RDSSA、RCSSA、CASSA、ALSSA和AIWSSA,也分别在11、9、11、12和4个函数上寻到了更优解,表明精英均值个体策略与选择反向学习策略在协助算法求解多峰函数时发挥了重要作用.因此,3种策略同时使用可有效提升SSA求解多峰函数的性能. 为了直观地观察7种SSA改进算法的收敛性能,本文选取几个具有代表性的函数绘制寻优收敛曲线如图4所示. 图4 改进SSA函数收敛曲线Fig.4 Convergence curves of functions for improved Salp Swarm Algorithms 在单峰函数f5和多峰函数f12上,在CASSA、ALSSA、AGHSSA和RDSSA陷入局部最优的情况下,MGSSA能很好地跳出局部最优,找寻更优解,其勘探能力较强.同时在f8,f13两个函数上,也可以观察到MGSSA在搜索过程中收敛速度和跳出局部最优的能力十分显著. 为了更好地验证MGSSA在求解工程约束问题时的性能,本文将MGSSA 与CASSA[15]、RDSSA[16]、RCSSA[13]、 ALSSA[18]、AIWSSA[26]和AGHSSA[27]6种改进SSA算法和基本SSA应用于拉压弹簧设计问题中的求解.同时利用罚函数法,在目标函数中加入惩罚项,将约束优化问题转化为无约束优化问题.将种群大小设为40,最大迭代次数设置为500,每个算法独立运行30次取最优求解结果比较,各算法参数设置同对应参考文献,比较结果如表5所示. 表5 8种算法求解拉压弹簧设计问题最优结果 拉压弹簧设计问题的目的是最小化拉伸或压缩弹簧的质量,如图5所示.此问题受最小挠度、剪切应力、浪涌频率、外径限制和设计变量的限制.设计变量是平均线圈直径D=x1(0.05≤x1≤2)、导线直径d=x2(0.25≤x2≤1.3)和活动线圈数量N=x3(2≤x3≤15).问题可以表述为 图5 拉压弹簧模型Fig.5 Model of tension/compression spring 目标函数: 约束函数: 从表5结果可以看出,在8种算法中,MGSSA求解结果最佳,RCSSA次之,RDSSA、ALSSA与AGHSSA在求解工程约束问题时效果相比于其他几个改进算法效果差. 本研究引入的选择反向学习策略,相较于传统的反向学习策略,减少了计算维度,同时保留了种群的多样性,改善了每代种群解的质量.在跟随者位置更新阶段引入的精英均值策略,通过均值个体和最优个体的有效引导,使算法的寻优速度加快,改善了标准SSA的收敛速度慢的问题,同时收敛精度大幅提升.黄金正弦变异策略的加入,使算法在前期在均值个体周围寻找更优,后期随机选择个体在周围进行搜索,既有利于前期加快收敛速度,又有利于后期跳出局部最优. 通过在14个基准测试函数上进行对比实验,验证了MGSSA相较于RDSSA、RCSSA、CASSA、ALSSA和AIWSSA的稳定性和先进性.通过拉压弹簧设计问题可以观察到MGSSA在求解工程约束优化问题时表现良好.在接下来的研究中,将进一步改进樽海鞘群算法并将其应用到现实问题的求解.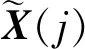
2.2 引入最优个体和精英均值个体的跟随者位置更新
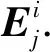
2.3 黄金正弦算子变异策略
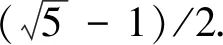
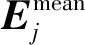
2.4 MGSSA算法伪代码
2.5 时间复杂度分析
3 实验仿真及结果分析
3.1 仿真实验设计及实验环境

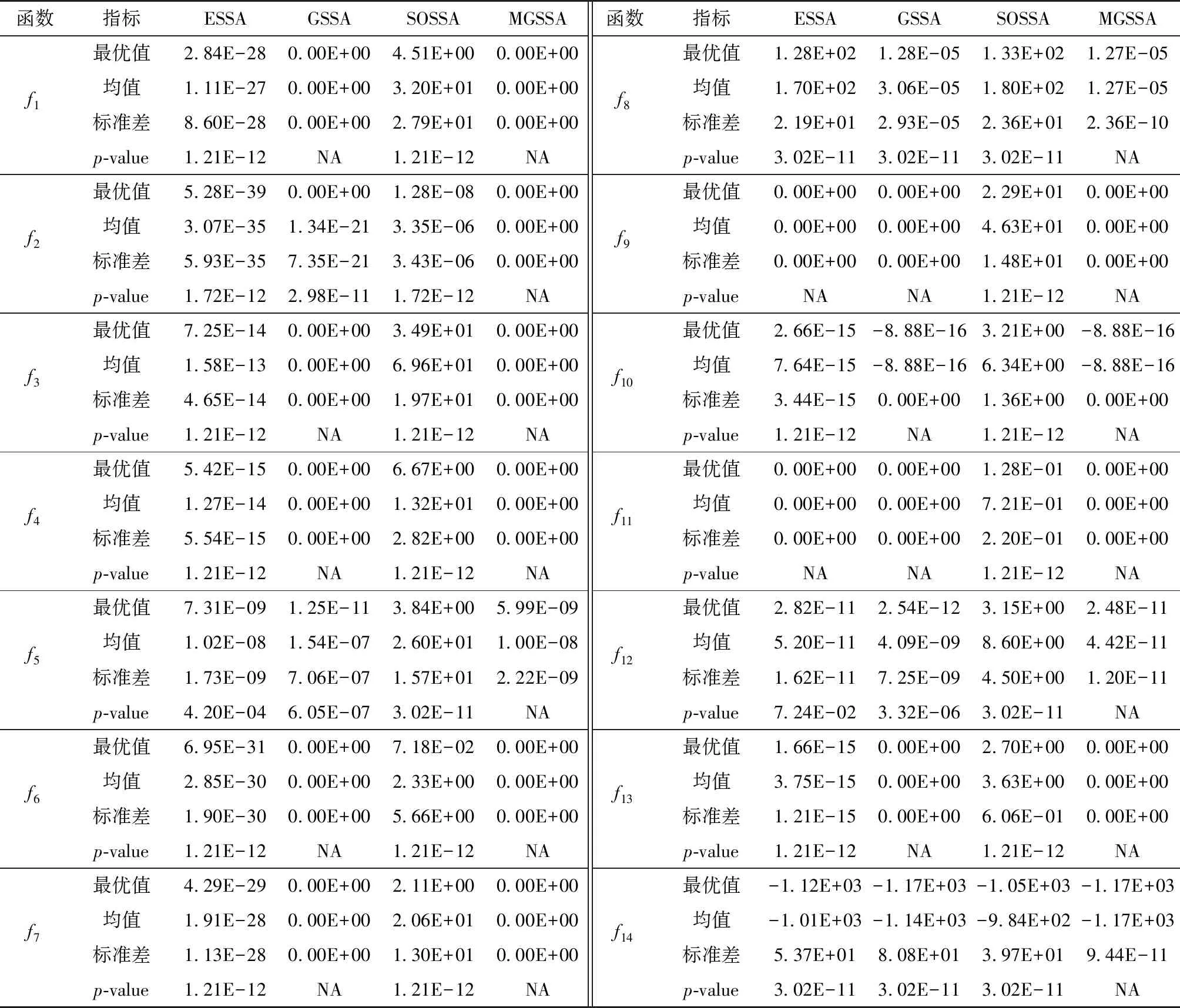
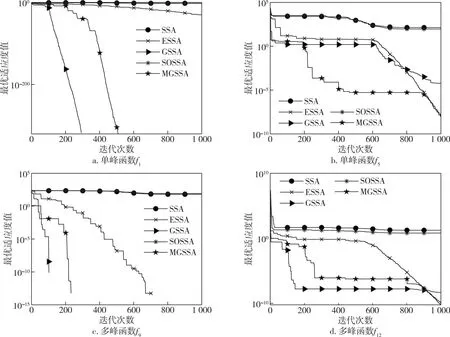
3.2 改进策略分析
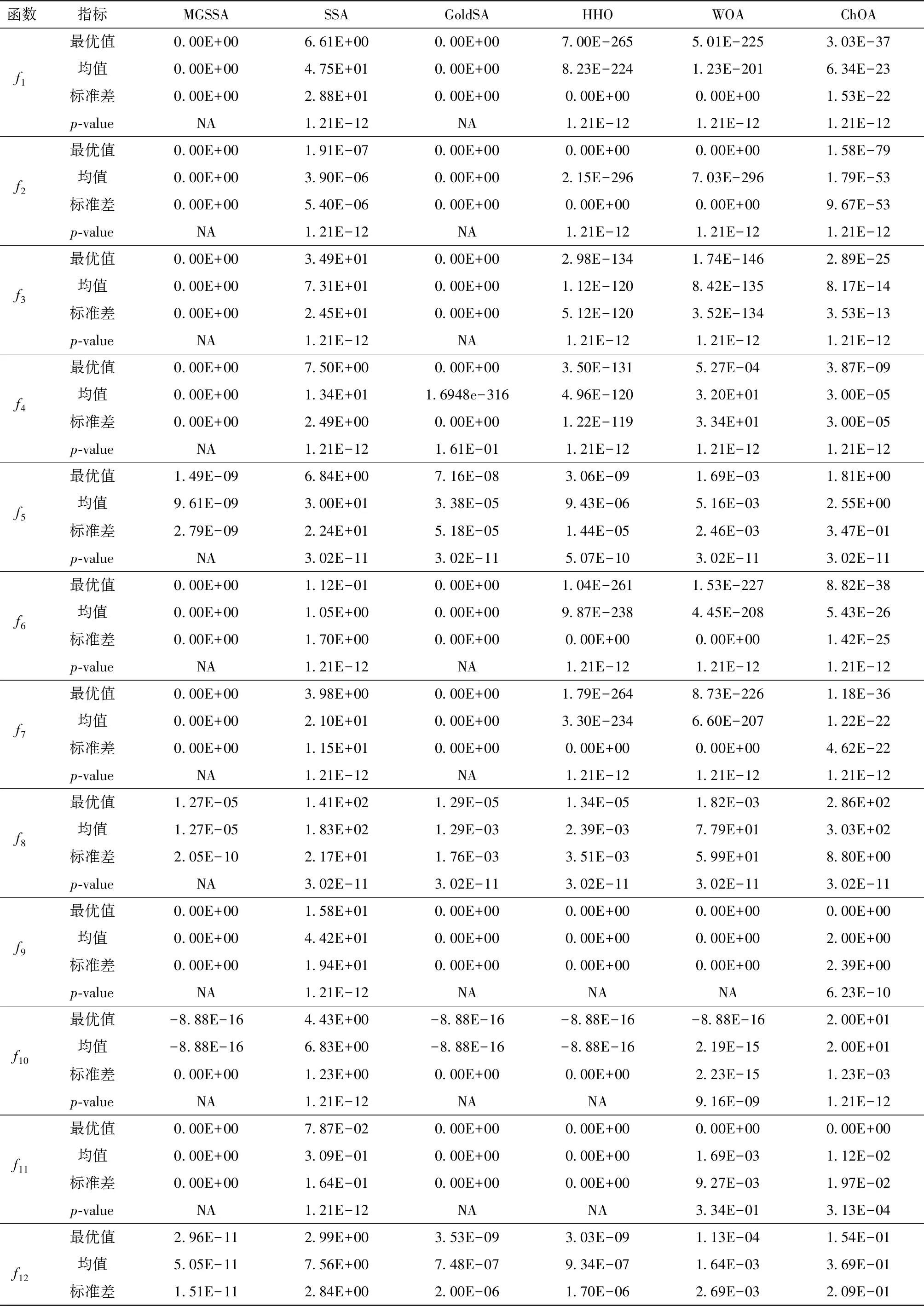
3.3 MGSSA与其他群智能算法比较
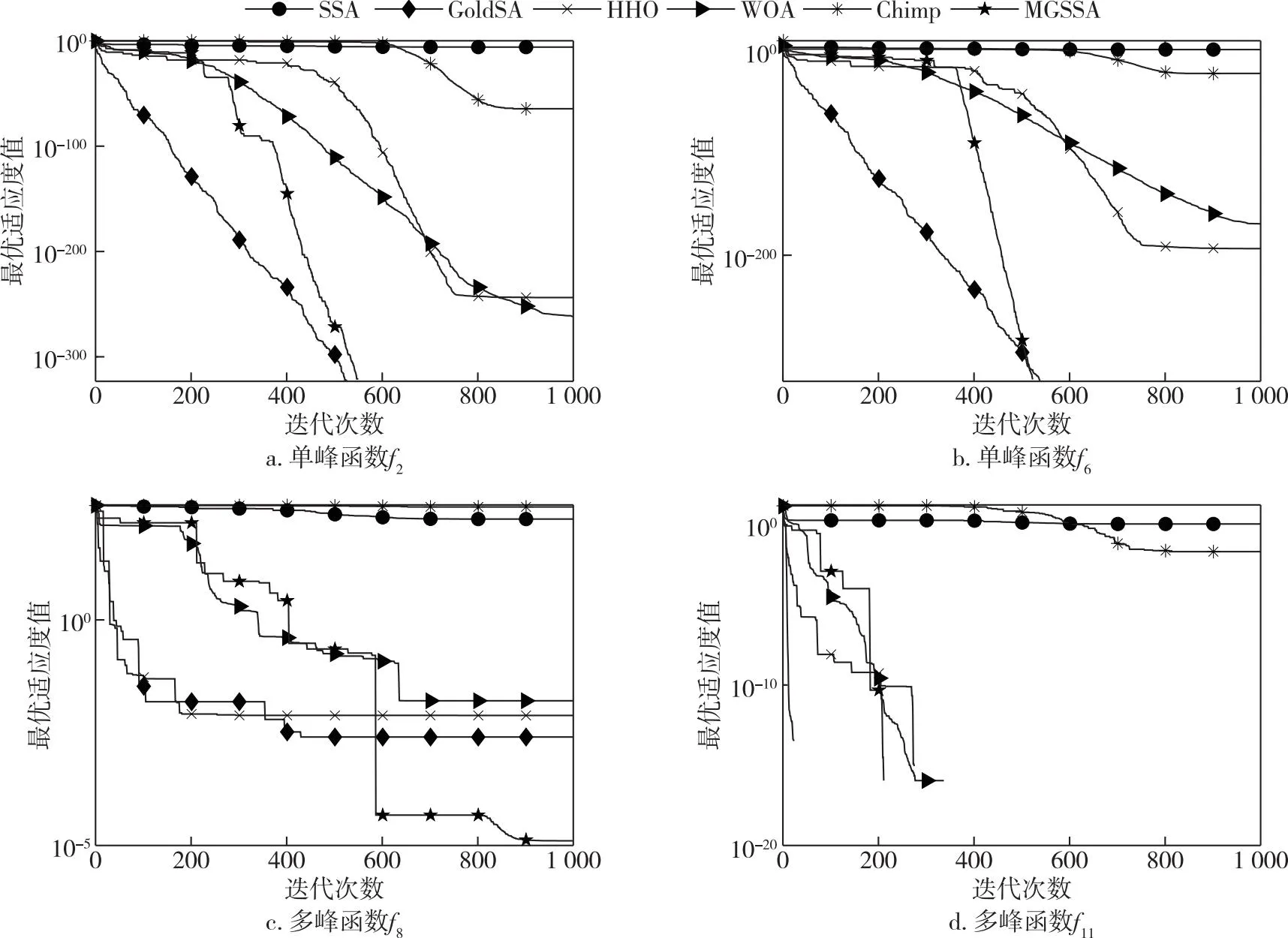
3.4 MGSSA与其他改进SSA算法


3.5 工程约束优化问题求解

4 结束语
