Neural network hyperparameter optimization based on improved particle swarm optimization①

XIE Xiaoyan(谢晓燕), HE Wanqi②, ZHU Yun, YU Jinhao

(∗School of Computer, Xi’an University of Posts and Telecommunications, Xi’an 710121, P.R.China)

(∗∗School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, P.R.China)

Abstract

Key words: hyperparameter optimization, particle swarm optimization (PSO) algorithm, neural network

0 Introduction

With the rapid growth of the artificial intelligence(AI) technologies, deep learning has achieved significant results in complex regression and classification problems, involving computer vision (CV), natural language processing (NLP), object detection[1], and so on.a neural network model needs to be trained to drive a satisfied accuracy.But there are a large number of hyperparameters which need to be configured during the training processing, such as learning rate,batch size, and optimizer.How to select appropriate hyperparameters to help training and explore the best neural network model has become a focus and a difficulty.

In the early studies, grid search was used to exhaustive search of parameter space.Later, an improved algorithm was implemented based on this called random search.Experiments have shown that, with the same number of search iterations, random search tries more parameter values compared with grid search, and reduces search time while ensuring model accuracy[2].However, these search methods cannot solve the parameter optimization problem of neural network very well.Ref.[3] mentioned that hyperparameter optimization is an NP-hard optimization problem, and most current approaches solve it by adopting metaheuristic algorithms.

Ref.[4] successfully used genetic algorithm(GA) for hyperparameter tuning.It is found that more and more metaheuristic and modified algorithms could be used to optimize neural networks, and some researchers choose to extend different exploration[3].The development of hybrid models can improve performance and the ability of complex optimization.Ref.[5] proposed an improved hybrid algorithm based on bat echo location behavior, combining local search to optimize weights, architectures, and active neurons.Ref.[6]introduced a combination of genetic and gradient descent to train networks.The proposed HGADD-NN method achieved good results on several benchmark problems.

Among most common algorithms, the particle swarm optimization (PSO)[7-8]is a more popular choice, compared with GA[9], grey wolf optimization algorithm (AWO)[10]and ant colony optimization(ACO), because of its less nodal parameters, efficient global search and easily concurrent processing.So, it is introduced into parameters selection of convolutional neural network (CNN).In Ref.[7], PSO is used for parameters decision of CNN and verified successfully in classification of CIFAR.This indicates that PSO is a feasible scheme for parameters optimization of CNN.To handle the different of value scopes and datatypes of hyperparameters, independent candidate particles were defined for different parameter in Ref.[7].But the initial position selected randomly would result in local optima trapped and the weakly local searching ability would entail a long convergent stage.Such a weakness may lead to a biased model even with the cost of additional calculations.Therefore, the improved PSO or integrating other heuristic algorithms become a striking field.Ref.[11] proposed a distributed PSO(DPSO)mechanism.The particles were updated and allocated in the master,and the fitness of different particles was calculated using multiple slaves.This strategy automatically and globally searches for optimal hyperparameters and dramatically reduces training time compared with traditional PSO, thanks to the distributed training method.Unfortunately, this idea only uses a distribution way to tackle long training time in the parameter configuration process.The cost of calculation is ignored.

The key problem to this issue lies in balance of the diversity of particle swarms and cost of convergence.In this work, an improved solution of PSO is proposed to aid in locating the best hyperparameter combination of specific network architecture easier.The following specific contributions are made.

(1) To response to the troubles caused by inconsistent data types and widely different value scopes of neural networks, the interval mapping method is adopted to data coding.The motivation of such design is to ensure the effectiveness of particles through a normalized strategy and to avoid the local evolution of swarm stem from randomly position selecting of original particles.

(2) By introducing mutation and crossover operations to increase the diversity of particles, the proposed algorithm solves the problems of the raw PSO, such as being easily trapped in local optima and low convergence accuracy during hyperparameter searching.

The rest of this paper is organized as follows.Section 1 discusses related work.Section 2 analyzes the motivation and describes the implementation of proposed algorithms in detail.Section 3 discusses the experimental environment and implementation scheme on different network structures and datasets.Section 4 summarizes the content of this paper.

1 Related work

In PSO[12], the optima seeking is converted to a process of traversing an-dimensional function with particles of a swarm.Each a potential solution to a given problem is viewed as a particle.PSO obtains the best solution from interaction of particles.When mapping the different value scope of hyperparameters into andimensional function, selecting of the best parameter combination can be figured out by PSO.

If there areNhyperparameters in the specific CNN, the value of each parameter ranges fromlowtoup.A particle can be denoted as{x1,x2,…,xN-1,xN}, and the performance is evaluated by a fitness function (often the loss function in CNN).The swarm is constructed originally with particles generated randomly by predefined value.The fitness value of each particle is calculated iteratively until reaching its best position or meeting the pre-set termination condition.The prior personal best position (gbest) and the global best position (pbest) is characterized as the intermediate results.Updating of particles can be given by Eq.(1) and Eq.(2).

where,vrepresents the velocity vector;wis the inertia weight utilized to balance the local exploitation and global exploration;r1andr2are random vectors uniformly distributed within the range of[low,up];c1andc2are acceleration coefficients, which are positive constants.

Above scheme, mentioned in Ref.[7] had been demonstrated be helpful to parameters tuning.However, there are many kinds of hyperparameter included in CNN, their datatype is also inconsistent (the number of convolutional kernels is recorded as integer, the learning rate is float, etc.).Moreover, the value scope of parameters in different layers show an enormous difference.The uniform format in coding will merge the effective attribute of particles and results a calculation error.However, differentiated coding format will increase the complexity of the swarm.Additional, when solving the problem with a large number of dimensions or complex and large datasets, PSO shows poor-quality results,usually falling into local optima trap.

To cope with this tricky situation, a series of solutions are proposed in this paper.The composite variabletype particles are mapped into an interval to ensure the effectiveness of particles update and to prevent the poor results due to significant differences in data sampling intervals.Then,the selection,mutation,and crossover operations of GA are introduced to add diversity of particles and avoid getting stuck in local optima during the parameter search process.Finally, an improved particle swarm optimization (IPSO) algorithm is proposed based on the above two improvement measures.

2 Methods

2.1 Hybrid particle coding

The parameters of CNN to be optimized selected in this paper include the number of convolution kernels, learning rate and batch size, etc., as shown in Table 1.

Table 1 Parameters to be optimized

It can be seen from Table 1 that the scope of parameters of int-type ranges from 6 ×(Parm1) to 120 ×( Parm4 ).In addition, a float-type parameter(Parm6) is also involved.Such a variety of value maybe leads to bias direction in updating procedure and unable to converge in severe cases.As a result, there needs an effective manner to remove this difference.To this end, the PSO advocate[7-8]can only independently characterizes particles for each parameter.As a result,initial value of each particle only occurs randomly in self-defined scope.Although the difference of parameter scope needs not to be considered, such a treatment may probably generate an unreachable position during searching.For example, in a two-dimensional space composed of Parm2 and Parm3, the value of Parm2 could not reach [1,3] and [8,11], marked as ‘☞’in Fig.1, due to the limiting of random function.Subsequently, particles generated will not overall coverage to initial swarm, while it would trap in local optima in iteration.

To avoid such incidents, a random sampling function conformed to uniform distribution is introduced in our scheme, which uniforms the coding of overall parameters.Meanwhile, Eq.(3) is used to mapping scopes of parameters to a normalized uniform.

where the lower bound and upper bound of a parameter are denoted aslowAreaandupArearespectively.The distribution of initial particles is presented as ‘☞’ in Fig.1.It is obvious that particles scattered steadily in overall interval.The global coverage of search space and completeness of swarm are guaranteed very well.

Fig.1 Schematic diagram of particle distribution before and after optimization

2.2 Genetic manipulation

In this paper, in order to increase the diversity of particles during the updating, the selection, crossover,and mutation operations of GA are added to the IPSO.The cross process of particles is shown in Fig.2.Suppose there areNparticles in the swarm, which are denoted as{X1,X2,X3,…,XN-1,XN}.After the calculation, the fitness values of each particle are marked as{F(X1),F(X2),F(X3),…,F(XN-1),F(XN)}.Firstly, the first two particles with higher fitness values are selected and recorded asXiandXj.The inter-section pointPis calculated using Eq.(4).TakingN=6 as an example, the selection result is shown in Fig.2(a).Then, using the inter-section pointPas the boundary, the particlesXiandXjare divided into four parts:Xi-front,Xi-after,Xj-front, andXj-after, as shown in Fig.2(b).Finally,Xi-frontis spliced withXj-after,andXj-frontis spliced withXi-after, then two new particlesXi-newandXj-neware formed, as shown in Fig.2(c).

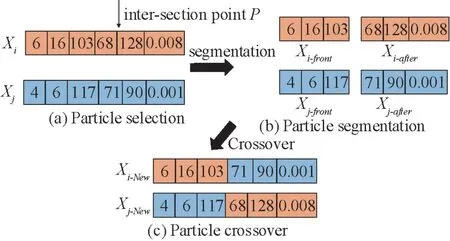
Fig.2 An example illustration of the crossover process

The schematic diagram of the particle mutation is presented in Fig.3,takingN=6 as an example.Firstly,the complete information of the initial particle would be obtained.Then, an integer value in [1,N] will be randomly generated,Ndenotes the total number of optimized parameters.Finally, a randomly generated number within the corresponding parameter scope of that position will replace the original value, and the mutation operation will be done.

Fig.3 Schematic diagram of mutation process

For the raw PSO method, particle position participating in the next iteration is determined by the optimal solution obtained from this searching round and the historical optimal solution.The update domain of raw PSO can be described by the zone, shown as dashed lines in Fig.4.The updating domain of raw PSO is limited to such a domain.It is only stopped in the optima of such local domain.If the global optima are escaped out of this interval,the final result will be deviated to the correct one.

The GA operations will help to jump out of this limitation by involving new particle.It can enhance the diversity of particles in iteration of swarm, and make the global optima be located easier.

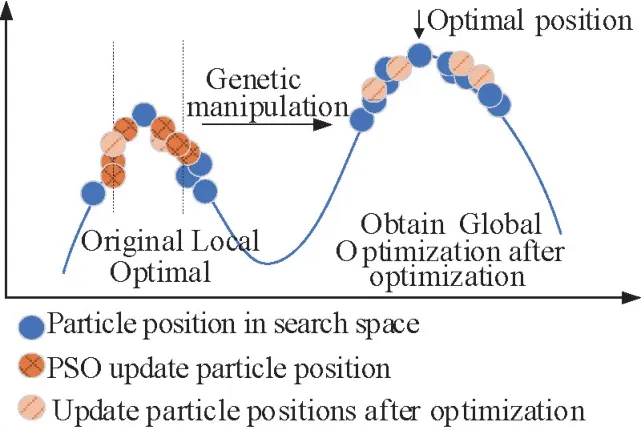
Fig.4 Comparison of particle positions before and after optimization

2.3 Overall scheme

The flow chart of hyperparameter configuration based on the proposed IPSO is shown in Fig.5, there are 3 steps as follows.

Step 1 Initialization of swarm and its particles.The learning factorsc1,c2, weight coefficientw,number of particles, and maximum particle speed need to be initialized at beginning.At the same time, it opens up a space to store local and global optimal values and randomly generates a specified numberNof particles to form a swarm according to the number and scope of parameters to be optimized.

Step 2 Calculate the fitness value of the particles.The values of each particle are sequentially sent to the designated neural network for training and testing, and the accuracy rate obtained will be selected as the fitness value of the particle and recorded.

Step 3 Particles updating.According to Algorithm 1, the particles in the current swarm are updated to complete the subsequent iteration.

Algorithm 1 Particle updating Input: Primitive swarm D(X), Fitness function F(X)Output: The updated swarm D(X)1: function update (D(X))2: Initialization max1 and max2 3 for:i in length ( D(X) )4: Evaluate F(Xi)5: set max1 and max2 6: end for 7: update gbest and pbest 8:new1 ,new2 = crossover ( max1 ,max2 )9: D(X) = mutate ( new1 ,new2 )10: return D(X)11: end function

Fig.5 Flow chart of the IPSO

3 Experiments and results analysis

3.1 Implementation details

The initialization of the algorithm is completed according to the parameters shown in Table 2.The proposed algorithm is verified under different network structures and data sets.The experimental environment of this paper is shown in Table 3.

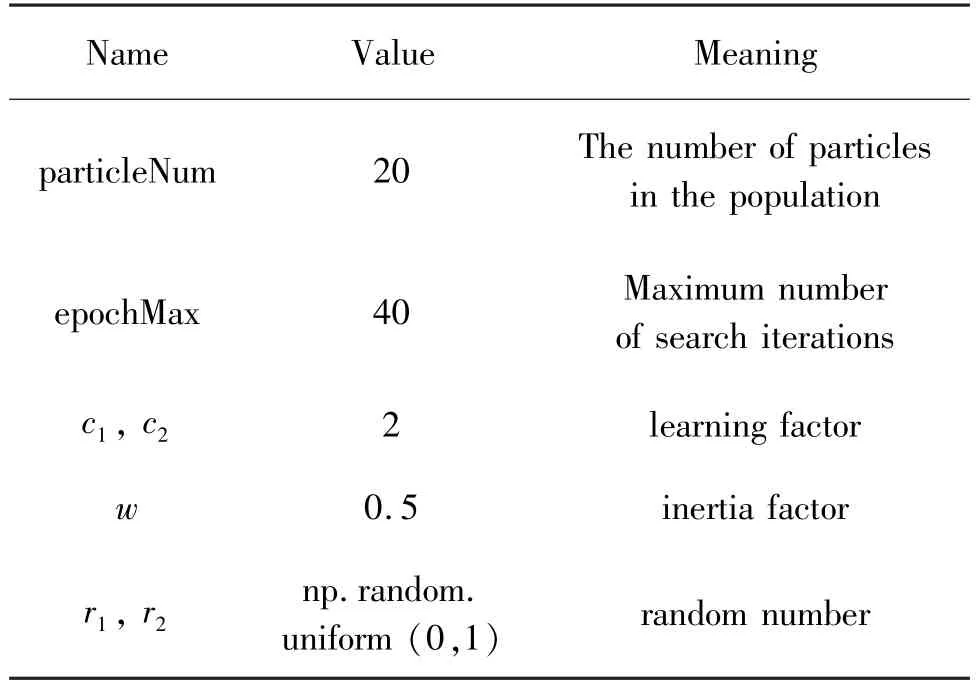
Table 2 IPSO algorithm related parameters

Table 3 Experimental environment setting

3.2 Experimental results and analysis

3.2.1 Under different network structures

In this work,LeNet-5,ResNet-18,VGG-16,MobileViT, and Long short-term memory (LSTM) are selected as the test objects.The MNIST was used on LeNet-5 and LSTM, the Flowers-Recognition was used on MobileViT, and the remaining networks tested with the CIFAR10.This presearch uses the parameters searched by the IPSO and PSO to complete the training task.The accuracy rate changes with epoch during the training are shown in Fig.6.It can be seen that for the same training epoch,no matter which neural network is used, the parameter configuration searched by the IPSO can make the neural network converge faster than the PSO.In addition, Fig.6 (c) and Fig.6(d) show more apparent difference in accuracy.

Fig.6 Accuracy rate change with Epoch

Using the IPSO and the parameters searched by the PSO to complete the training, the final accuracy rate is compared in Table 4.It is clear that, after structure tuned by IPSO, the CNN model can finally obtain higher accuracy, compared with tuned by PSO,among which the accuracy rates are increased by about 0.4%,1.9%, and 4.5%, respectively.On the ViT model, the network built by the IPSO can finally complete the image classification tasks with an accuracy rate of 66.21%, about 13% higher than that by the raw PSO.IPSO and PSO have achieved similar accuracy on the recurrent neural network.On the ViT model experiment, IPSO and PSO only have a difference of 1 in parameter 1, but the final network structure gains a significant difference due to the layer-by-layer accumulation.Meanwhile, although the data number of Flowers-Recognition used in this paper is small, different parameter configurations will still bring obvious difference of performance.LSTM is more inclined to the application of NLP.At the same time, this paper only considers two network-related parameters, the hidden state and the number of recurrent network layers.Although the difference between them will still change the number of parameters, the extraction effect of changing data feature is not obvious, which can be to negligible.

Table 4 Comparison of the accuracy of different algorithms on different network structures

3.2.2 Under different datasets

To get the effectiveness of the IPSO proposed in this paper on the hyperparameter seeking, three datasets of MNIST, Fashion-MNIST and CIFAR10 are selected for verification.

(1) The MNIST dataset includes 70 000 handwritten digital images.The training set contains 60 000 samples, while the test set contains 10 000 samples.The dataset is categorized into 10 classes related to 10 numerals.

(2) The Fashion-MNIST dataset contains 10 categories of images: T-shirt, trouser, puller, dress, coat,sandy, shirt, sneaker, bag, and ankle boot.The training dataset has a total of 60 000 samples, and the test dataset has a total of 10 000 samples.

(3) The CIFAR-10 dataset includes 60 000 color images from 10 categories, with 6000 images per category.These 10 different categories represent aircraft, cars, birds, cats, deer, dogs, frogs, horses, boats, and trucks.The training set contains 50 000 samples (83% of the original dataset),while the test set contains 10 000 samples (17% of the original dataset).

The parameters searched by the IPSO on the above three data sets can have 99.58%, 93.39%,and 78.96% accuracy when training the neural network.Compared with PSO, the accuracy has increased by about 0.1%,0.5%,2%, respectively.Compared with the SSO[13], the same accuracy has been achieved on the MNIST dataset meanwhile.On Fashion-MNIST and CIFAR10, the accuracy has increased by 0.36%and 5.83% respectively.Compared with the DPSO[11], the model accuracy obtained using IPSO on MNIST and Fashion MNIST is slightly higher, and the final results are shown in Table 5.In addition, in order to compare with the WOA[10], the network’s optimization parameters are adjusted to be consistent with those in GWO,including batch size,epochs,and optimizer.The results are shown in Table 6.From the table, it can be seen that the IPSO algorithm’s search for parameter combinations completed training on the Fashion-MNIST dataset has a higher accuracy on the test set than GWO algorithm.

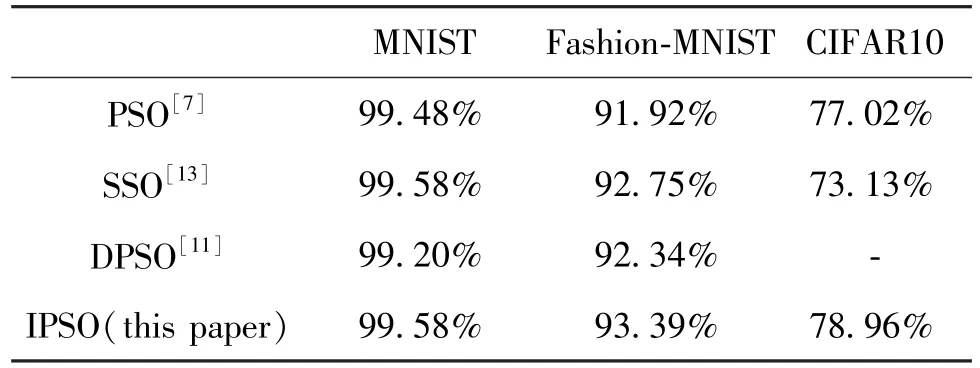
Table 5 Comparison of the accuracy of different algorithms on different network structures

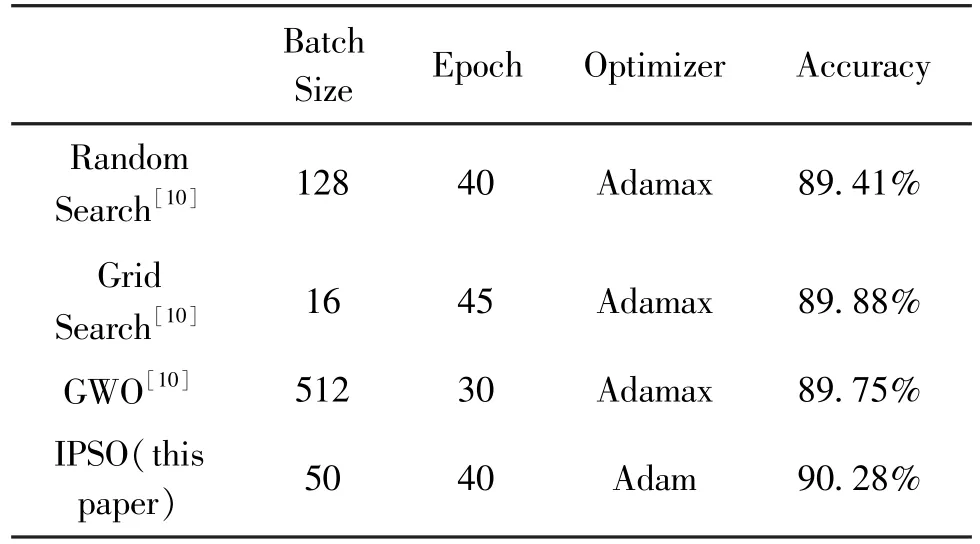
Table 6 Accuracy comparison on the Fashion-MNIST dataset

4 Conclusion

This paper proposes an IPSO algorithm that integrates GA to address the issues of traditional PSO,such as easily falling into local optima and low convergence accuracy in the process of seeking.Finally, the performance is verified by using different types of neural network models and datasets.Experimental results show that the proposed IPSO achieves higher accuracy than traditional PSO on CNNs and ViT models, tested with Fashion-MNIST and CIFAR10 datasets.Moreover, with optimized parameter configurations, the model is more stable and converges faster during training.However, this paper only considers a limited number of parameters to be optimized, while other parameters affecting the neural network structure, such as the depth and number of convolutional layers, can also be searched for the optimal solution.Therefore, in the future, it is worth considering the fusion of parameters at different levels to find the optimal network structure and model parameters for better model performance.