Research on dual-command operation path optimization based on Flying-V warehouse layout①

LIU Jiansheng(刘建胜),YUAN Bin,YANG Zan②,ZHONG RAY Y

(∗School of Advanced Manufacturing, Nanchang University, Nanchang 330031, P.R.China)

(∗Department of Industrial and Manufacturing Systems Engineering, University of Hong Kong, Hong Kong 999077, P.R.China)

Abstract

Key words: Flying-V, access collaboration, path optimization, dynamic decoding, genetic algorithm

0 Introduction

Logistics optimization in warehouse management can effectively reduce the operating costs for enterprises.Among all logistics processes, access operation is the most labor-intensive and costly, with costs accounting for up to 55% of the total operating expenses of a warehouse[1].Previous studies have indicated that optimizing access operation is crucial for improving warehousing efficiency[2].The time spent on access operation is a key indicator for measuring operational efficiency, and it is closely associated with the selection of access operation path.Therefore, reducing the travel distance of access operation is capable of enhancing the efficiency of warehousing management operations.

In recent years, researchers have studied access operation paths in warehouse by taking into account different warehouse layouts and order distributions under the assistance of heuristic algorithms such as genetic algorithms[3-4], ant colony algorithms[5-8], and particle swarm algorithms[9-12].To reduce the access cost of goods, Ref.[13] proposed the Flying-V layout mode as an innovative warehouse layout, proving that this non-traditional layout can shorten travel distance by 10% - 20% compared with traditional layout in terms of picking efficiency.However, most current studies focus on single-command operation mode[14-19]by maximizing their respective operational efficiency without considering the association of access operations,where only deposit or picking operations are conducted during a single operation trip.Although this single-command operation mode is simple and easy to execute, it leads to problems such as idle trips and resource waste, indicating the need for improving overall operation efficiency.Therefore, this paper focuses on optimizing the dual-command operation path of Flying-V layout warehouse.

1 Problem description and mathematical model

1.1 Problem description

In this study, a batch of ordered goods required depositing while another batch required picking, and the objective is to complete the order operations with the shortest total operation path.The warehouse layout adopted Flying-V type layout, and the plane layout of the entire warehouse is shown in Fig.1.The P&D(pick and deposit) point is the entrance and exit of the warehouse.To facilitate the study of warehouse management path optimization, certain assumptions have been made.

(1) During the operation, the freight vehicle has a load limit ofQ,allowing for multiple operations to be carried out.

(2) It is assumed that walking distance on both the left and right sides of the passage are negligible.

(3) In addition, turning back and walking in the passage is permitted.

(4) The demand for goods in every order is less than that of the freight vehicle’s load capacity, and the freight vehicle can only access each location once.

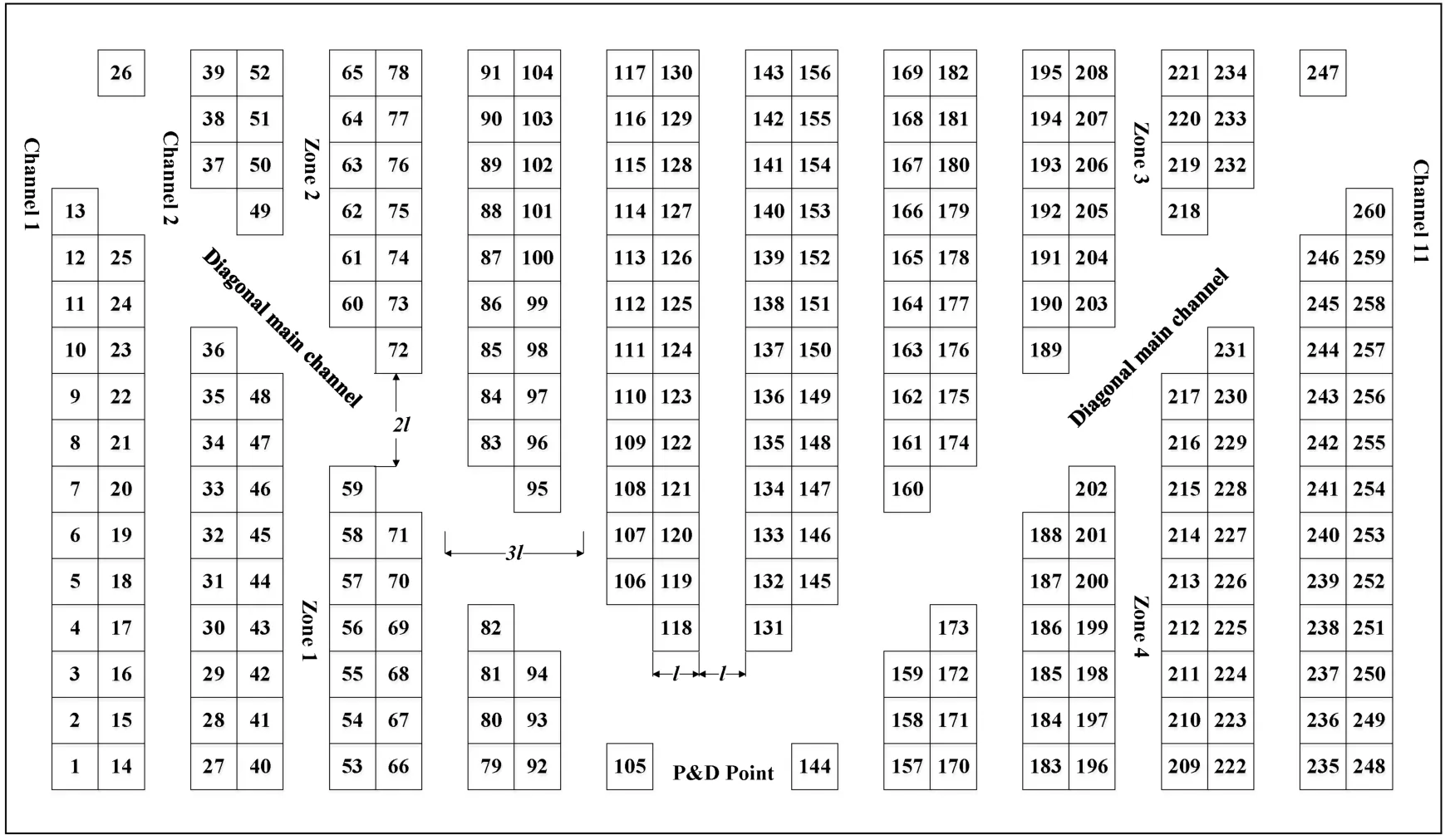
Fig.1 Flying-V warehouse layout

1.2 Parameter design

Fig.1 shows the picking area number and cargo space number.The cargo space number ranges from 1 to 260, from left to right and bottom to top, with the P&D point number being 0.The warehouse layout is divided into four picking areas, starting clockwise from the lower left corner of the warehouse, and is divided into Zone 1, Zone 2, Zone 3 and Zone 4.Regardless of the height of the cargo space, the length and width of the shelf arel, the width of the picking channel isl, and the width of the diagonal main channel is 2l.

To represent the corresponding cargo space number, a virtual coordinate system is utilized in the plane layout.The array {k,x,y,z} is employed, wherek(k= 1,2,3,4) indicates the cargo area number,x(x=1,2,3,...,11) represents the number of channels,y(y= 1,2,3,...,ymax) depicts the number of rows of shelves starting from the diagonal main channel, andz(z= 1,2) indicates the left and right sides of the channel; specifically,z= 1 denotes the left side of the channel, andz= 2 represents the right side of the channel.For example, {2,5,10,1} represents Zone 2, the 5 th channel, the 10 th space from the diagonal main channel upward, the shelf on the left, i.e., cargo space number 102 in Fig.1.

1.3 Distance matrix calculation

To optimize the distance to complete the order access operation, it is necessary to calculate the distances between any two points, including the distance between the P&D point and the cargo space point, as well as the distance between two cargo space points.

(1) Distance between the P&D point and the cargo space pointi.

1) When the cargo space is located in Zone 1 (the same for Zone 4), that is,ki= 1 :

2) When the cargo space point is located in Zone 2 (the same for Zone 3), that is,ki= 2 :

(2) Distance between any two cargo space points:

1) When two cargo space points are in Zone 1 (the same for Zone 4),ki=kj= 1 :

2) When two cargo space points are in Zone 2 (the same for Zone 3),ki=kj= 2 :

3) When two cargo space points are located in Zone 1 and Zone 2 respectively (the same for Zone 3 and Zone 4),ki= 1,kj= 2 :

4) When two cargo space points are located in Zone 1 and Zone 3, respectively (the same for Zone 2 and Zone 4),ki= 1,kj= 3 :

5) When two cargo space points are located in Zone 1 and Zone 4, respectively,ki= 1,kj= 4 :

6) When two cargo space points are located in Zone 2 and Zone 3, respectively,ki= 2,kj= 3 :

1.4 Modeling

The goal of optimization is to minimize the distance to complete the order access process while returning to the entrance for multiple operations.The mathematical model for the path problem can be designed as follows.

Objective function is

Constraints:

Decision variables:

where,

S: total traveling distance when all order operations are completed;

i,j∈Ω: all cargo spaces to be picked and the starting point; andi= 0 indicates the P&D point;

dij: the shortest distance between cargo spaceiand cargo spacej, calculated according to Eqs (1)–(8);

Qi: load when starting from pointi;

Q0: initial load from P&D point;

Q: maximum load;

qi: required weight at cargo space pointi;

The objective Eq.(9) seeks to minimize the distance required to complete all orders; Eq.(10) and Eq.(11) guarantee that each picking point has one and only one previous and subsequent task; Eq.(12)defines the range of values for the decision variables;Eq.(13) and Eq.(14) prohibit overloading during the operation.

2 Algorithm solution

To solve the aforementioned model,a dynamic decoding genetic algorithm is implemented.Algorithm 1 provides the corresponding pseudo-code, and the corresponding elaboration for the following steps are shown in subsections 2.1 -2.6.

Algorithm 1 The dynamic decoding-based genetic algorithm Input:Population size:N, Crossover probability: Pc,Mutation probability: Pm, Number of orders:Num_orders, Required weight at each point:q, Operation type:label, Maximum load:Q Output: Optimal individual:xbest 1.Initialize population with random candidate solutions, shown in subsection 2.1.2.Decode (using Algorithm 2) and evaluate each candidate solution shown in subsection 2.2.3.g = 0 4.While terminate condition is not satisfied do 5.Select parents shown in subsection 2.3.6.Crossover operation shown in subsection 2.4.7.Mutation operation shown in subsection 2.5.8.Decode (using Algorithm 2) and evaluate new candidate solution shown in subsection 2.2.9.Select individuals for the next generation shown in subsection 2.3.10.g = g +1 11.End while

2.1 Initialization

To initiate the optimization process, the value for the population sizeN, cross probabilityPc and mutation probabilityPm are defined.The chromosome code is randomly generated as 1×No,whereNo refers to the order quantity.This process is repeatedNtimes to generate anN×No population.

2.2 Decoding

The natural number code is used, with numbers ranging from 1 toNo and 0 for the P&D point number.The sequence of codes indicate the access sequence of the cargo space points.

If there is no load limit, the problem could be simplified into a standard TSP problem, which only requires visiting each cargo space point in sequence and returning to the starting P&D point without the need for additional decoding.However, due to the load limit, it is necessary to go back and forth to the starting point during the access operation.Therefore,0 is inserted into the code sequence and the load is dynamically calculated to determine the position where 0 is inserted.The dynamic decoding steps are as follows.

(1)Considering the limit state, at a certain time during the access operation, all goods ordered in all cycles are on the freight vehicle and are decoded according to the load limit of the freight vehicle.If the freight vehicle carrying 1-iorders is not overweight,the first cycle of decoding is(0,p1,p2,...,pi,0).

(2)Cargo space pointi+ 1 is added to the decoding cycle to simulate the load of the previousi+1 cargo space points.The order weight to be warehoused is taken as the initial load to simulate the access operation of each cargo space point and calculate the load of each cargo space point.If a middle point is overweight, it means that the decoding fails, and the first decoding cycle is still (0,p1,p2,...,pi,0).If no overweight occurs during the intermediate process, it means that the decoding is successful, and the decoding is(0,p1,p2,...,pi,pi+1,0).Then cargo space pointi+2 is added to the decoding cycle, and the above steps are repeated until pointi+nbecomes overweight in the simulation process.At this point, the decoding is considered as failure, and the next cycle of decoding starts.

(3)Steps (1) and (2) are repeated until all order points are decoded successfully.

Algorithm 2 presents the process of dynamic decoding.

Algorithm 2 The dynamic decoding algorithm Input:Individual:x, Number of orders:Num_orders,Required weight at each point: q, Operation type:label, Maximum load:Q Output: Decoded individual:x_d 1.For i =1 to Num_orders 2.Calculate the initial load of the first i orders Q0.3.x_d =0 4.For j = 1 to i 5.x_d = [x_d,x(i)]6.If label(j) = = 1 7.Qi = Qi-1 + q(j)8.Else 9.Qi = Qi-1 –q(j)10.End if 11.If Qi < = Q 12.Continue 13.Else 14.x_d = [x_d,x(i -1)]15.save decode fragment x_d 16.break 17.End if 18.End for 19.End for 20.Restores the decoded fragment to a one-dimensional array x_d

2.3 Selection operation

The fitness value is the value of the objective function.To optimize the population and improve the fitness of individuals, the principles of ‘survival of the fittest’ in nature are followed.Inspired by the replication operation in bacterial foraging algorithms, half of the individuals with poor fitness value are directly eliminated, while the other half individuals with good fitness values are copied.To prevent the subsequent crossover and mutation operations from degrading the individuals with the best fitness value, an elite retention strategy is adopted.This strategy ensured that the fittest individuals are preserved in the population and not lost during the optimization process.

2.4 Crossover operation

To increase the diversity of the population and improve the global search ability, double-point crossover is adopted.This allows the same chromosome crossover operation to generate new chromosomes, which further enhances the optimization process.In double-point crossover, two crossing points are randomly selected on the two parent chromosomes.The chromosome between the two points is copied to the corresponding chromosome of the other parent, and the previous duplicated code is removed.This process increased the diversity of the population and allowed for a more efficient search for optimal solutions.

2.5 Mutation operation

The mutation operation uses double-point exchange mutation, which further increases the diversity of the population.In this operation, two point are randomly generated in the chromosome.The codes of the two points are then exchanged to complete the mutation operation.This approach allowes for the exploration of new solutions and prevents the population from getting trapped in a local optimum.By introducing random changes to the chromosomes, the algorithm is able to search for more optimal solutions across the solution space.

3 Simulation experiment

Experimental environment: Windows 10 operating system, Intel (R) Core (TM) i5-10400 CPU @2.9 GHz processor, 32.0 GB RAM, developed with Matlab R2018a.

To demonstrate the effectiveness of the proposed algorithm, a randomized example with 20 orders and their corresponding demands are created, which is shown in Table 1.The cargo space number is designed according to the model parameters, and the maximum load (Q) of the freight vehicle is set to 20 kg.For example, the second order requires picking 4 kg of goods from the No.32 cargo space.To ensure a sufficient population size to 200, which is 10 times the number of orders, set the evolution times to 500.The selection of crossover and mutation probability is determined through experiments.An orthogonal table is used to select the crossover probability ranging from 0.1 to 0.9 with an interval of 0.1 and the variation probability from 0.01 to 0.1 with an interval of 0.01.The optimal values are obtained by changing the parameters and running the process 20 times.Calculate the average value and find that the optimal crossover probability is 0.8,and the optimal mutation probability is 0.1.

The reason for selecting a large probability of crossover and mutation is analyzed.Since the replication is used for selection, the average fitness value of the population, i.e., the objective value, would decrease rapidly, but at the same time, the diversity of the population and the global search ability decrease rapidly.Therefore, selecting a large probability of crossover and mutation can effectively increase the diversity of the population and the global search ability,leading to better optimization results.

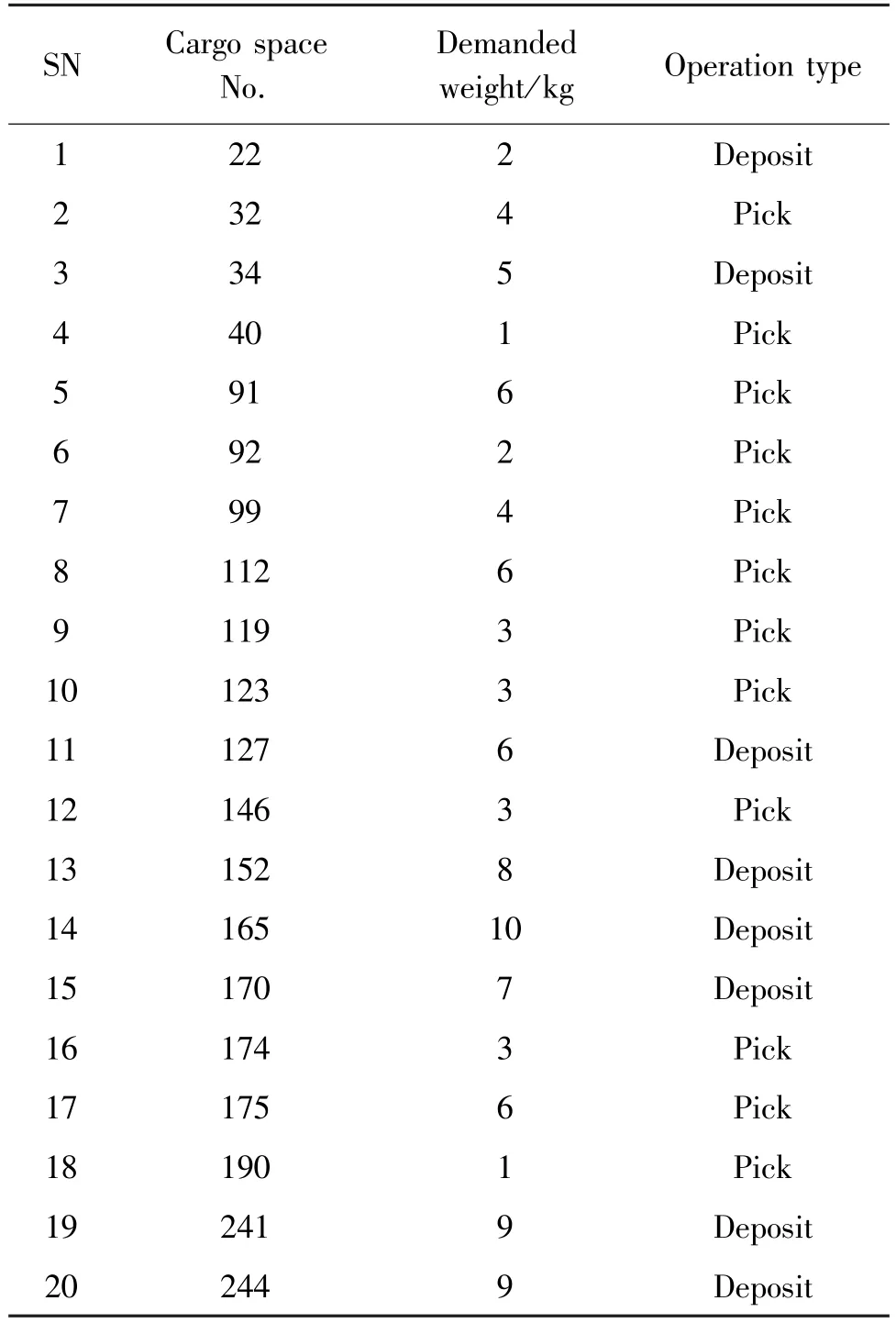
Table 1 Order demand

Three different access operation schemes are adopted, and genetic algorithms are used to solve the optimal path.

Mode 1: separated deposit and picking operations, with the deposit order operation and picking order operation conducted separately.The shortest operation distance calculated is 277.55.

Mode 2: ‘deposit first and then pick’ operation.After all the goods on the freight vehicle are deposited,the freight vehicle does not return to the entrance and exit but continues with the picking operation.The shortest operation distance calculated is 234.68.

Mode 3: the deposit and picking operations are completed simultaneously in an access collaboration operation.The shortest operation distance calculated is 190.40.

Calculation results are presented in Table 2 and Figs 2 -4.

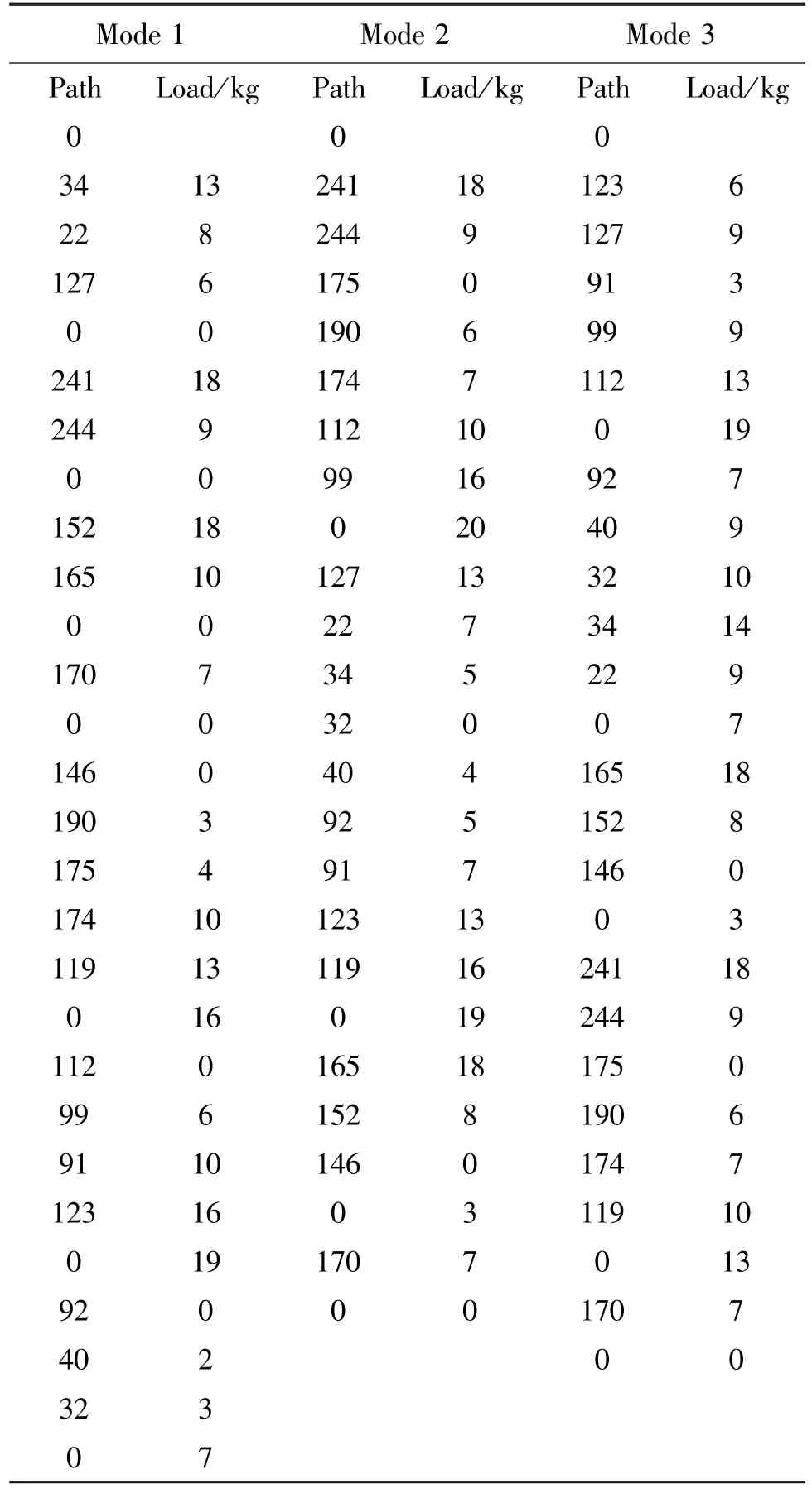
Table 2 Optimization results of three different modes

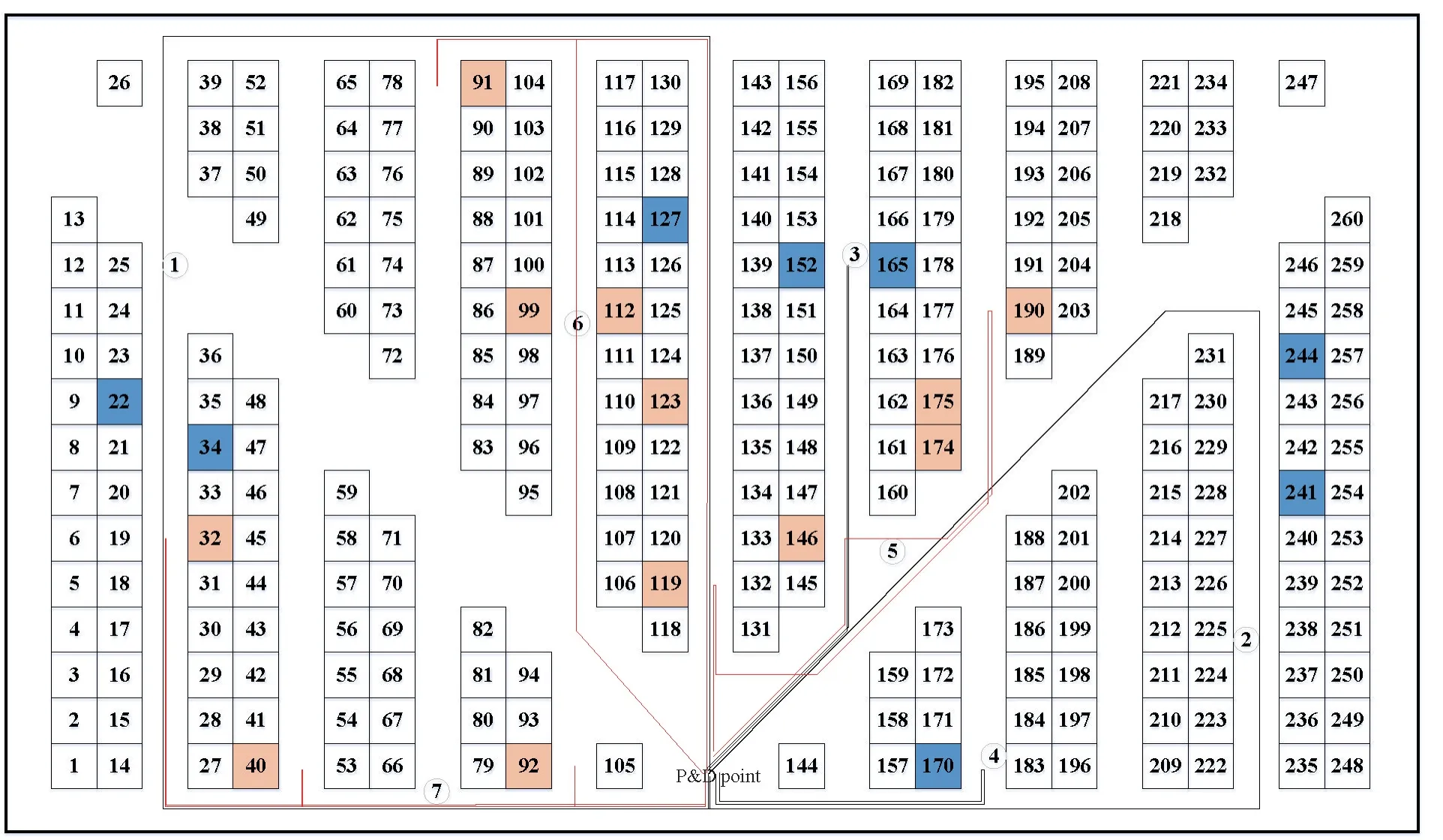
Fig.2 Optimization path of Mode 1

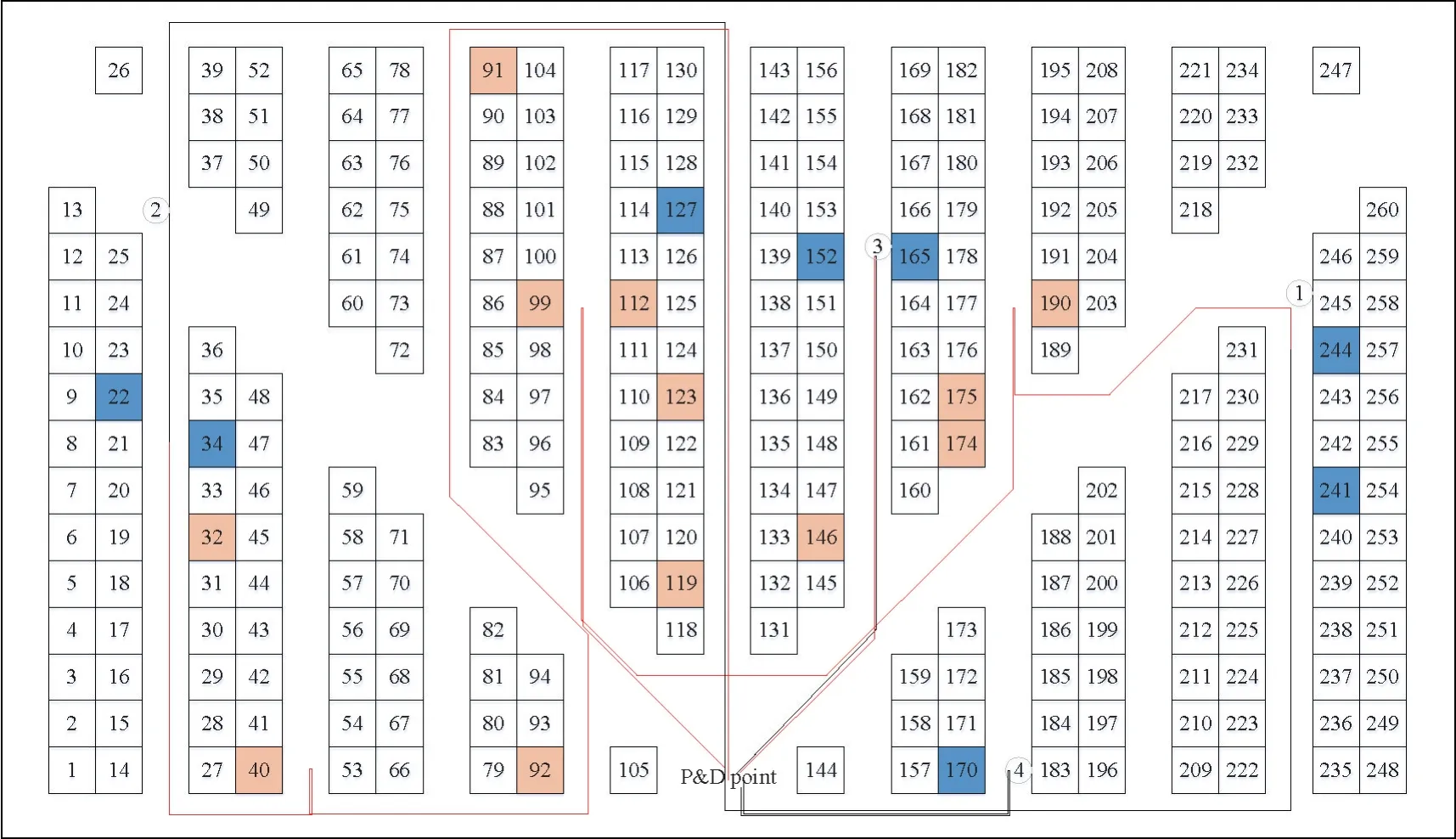
Fig.3 Optimization path of Mode 2

Note: in the table, the freight vehicle follows the path 0→34→22→127→0, starting from the entrance and carrying 13 kg of cargo.When arriving at cargo space No.34, 5 kg of cargo is deposited, and when reaching cargo space No.22, 2 kg of cargo is deposited.Finally,6 kg of cargo is deposited in cargo space No.127 before returning to the entrance and exit to load cargo.In the figures, the dotted line indicates picking cargo for stock out, while the solid line indicates depositing of cargo.

The calculation results, Table 2, and the simulation path diagrams show that all three modes are operated with maximum load to reduce trips to and from the entrance and exit and shorten the operation path.Mode 1 has the longest path, while Mode 2 is slightly shorter with some optimization.Mode 3 has the shortest path,which is 31.4% shorter than Mode 1 and 18.8% shorter than Mode 2.The reason is that Mode 1 has noload when travelling to and from the entrance and exit.After deposit, it returns to the entrance and exit without any load, and when picking the cargo, it also goes to the cargo spaces with no load.Although Mode 2 can avoid no-load at the entrance and exit, it is not optimized as a whole.Mode 3 is optimized as a whole while avoiding no-load, resulting in the most optimal outcome.

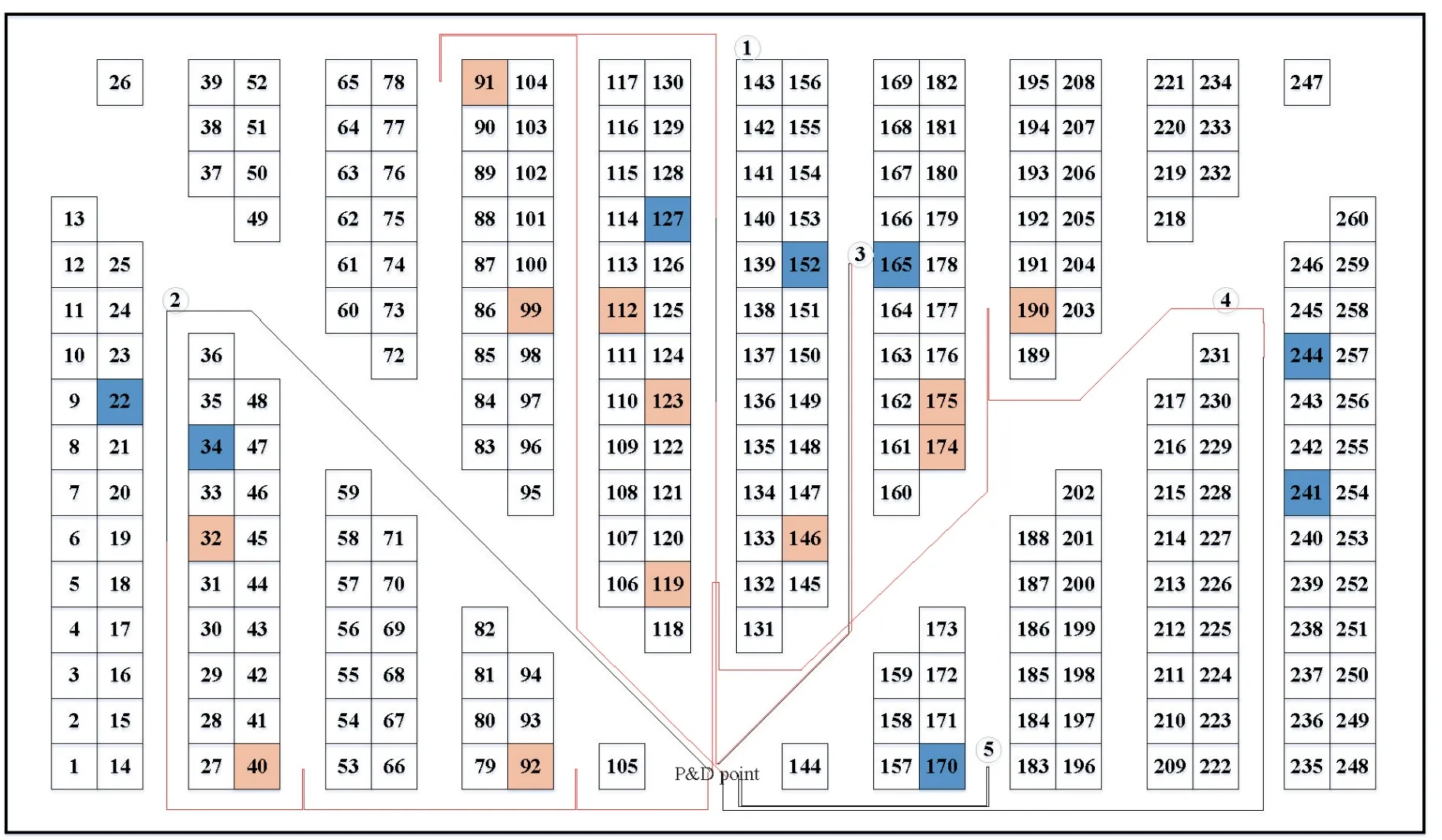
Fig.4 Optimization path of Mode 3

To prove the effectiveness of the algorithm for access cooperative operation, numerous experiments have been conducted.The orders between 20 and 100 are randomly generated for calculation.For each example of different order quantity, the calculation is repeated 100 times, and the average value is calculated, as shown in Table 3 and Fig.5.The experimental results show that in the non-traditional Flying-V warehouse layout mode,the operation in Mode 3 can be shortened by an average of 25% – 35% compared with the operation path in Mode 1,and 13%–23% on average compared with the operation path in Mode 2.With an increase in order size, the optimization effect of Mode 3 becomes better.

4 Conclusion

This paper establishes a Flying-V layout warehouse path optimization model for dual-command operation path optimization of Flying-V layout warehouse management and proposes a dynamic decoding genetic algorithm.The simulation optimization experiment is conducted by randomly generating orders,and the optimization paths of three solutions, namely, separated operation of deposit and picking, ‘deposit first and then pick’ operation, and access collaboration operation, are calculated.The experimental results show that the access collaboration of dual-command operation can effectively reduce no-load, shorten the path,and improve efficiency.

Table 3 The average of 20 independent runs of three modes for different number of orders

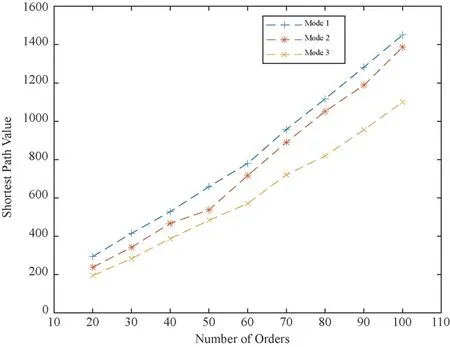
Fig.5 Average optimization results of three modes for different number of orders