邻近海底基准站坐标时序联合处理模型

孙 悦,薛树强,韩保民,肖 圳

1.山东理工大学建筑工程与空间信息学院,山东 淄博 255049; 2.中国测绘科学研究院,北京 100036

GNSS的广泛应用,使得陆域地壳运动观测网络已经非常密集,且实现了长期连续观测[1-3]。1980年提出的GPS与声学测距相结合的联合观测系统让建设高精度海底大地测量的海底参考点成为可能[4]。经过多年的发展,该方法理论与技术得到了不断的完善[5-7]。水下定位精度主要受复杂海洋环境的影响,特别是海洋声速场时空变化误差的影响,例如,季节性温度和流场变化会对声速剖面整体产生影响等[8-9]。近年来,海底高精度定位方法也不断完善[10-11],实现了声速误差的有效补偿[12-13]。需要指出的是,海底基准网采用对称设计,有利于减小声速误差影响[1,14-15]。

文献[16]提出在海底布设多个基准点构成的基准网,其基准点均匀地分布在半径近似等于水深的圆上,可实现更为准确的海底地壳运动监测。海底多站联合观测技术一直沿用至今,已实现海底位移监测和海底板块扩展监测[17-18]。由于供电不足等原因,海底基准站难以全部正常工作,更难以保障长时间连续观测。倘若海底一组基准站即将供电不足,则需要重新布站或更换电池,考虑到水下作业的固有成本和技术难度,通常在每个海底基准站附近安装一个新的海底基准站[19]。中心点法是目前国际上开展海底地壳运动监测普遍使用的方法,而换站补偿是该方法必须采用的策略。当然,原位观测是海底基准维护的理想途径,但实现原位观测具有较高的深海工程作业难度。因此,联合多个间断基准站坐标时序获取海底构造运动信息就成为实现海底大地测量监测的重要课题,文献[15]提出采用海底基准站网的中心点作为虚拟观测,通过估计虚拟观测中心点的偏移量进行形变监测。近20年太平洋西岸附近建立的世界上最为密集的地壳运动观测网络清晰记录了一系列大型地震引起的形变等,实现了灾害过程模拟[20-22]。文献[23]利用日本东北大地震前的数据对日本海底地壳运动观测系统进行了评估,结果表明,海底基准站网平面定位精度已达到厘米级,高程方向定位精度也可达到10 cm。

综上所述,目前国际上主要采用中心点法和新旧基准站换站补偿方法,实现海底高精度、长时序、连续观测,并以此为基础开展海底地壳运动监测。虽然虚拟中心点方法可用于海底区域地壳运动监测和形变分析,但无法获取海底基准站网中各基准站协议坐标,无法为海洋大地测量和海洋导航提供参考框架,也难以实施精细化质量控制,因此笔者认为这不是海底基准建立与维持的最佳途径。为此,笔者借鉴国际地球参考框架(ITRF)构建方式[24],提出了基于协议参考历元的站坐标与站速度联合估计方法,可为水下导航定位服务提供实时、动态、高精度参考基准。

1 海底坐标时序多站联合处理模型

假设整体海底基准网与地壳存在一个共同的运动速度,设定一个参考历元(建议采用观测周期内的中间时刻),并将每个站点在该参考历元处的坐标作为未知参数,与海底基准网的整体运动速度进行联合估计,简称联合估计模型。设有I个海底基准站,第i个海底基准站在t0时刻的坐标xi0,假设所有海底基准站在该时刻具有相同的速度v0,则t时刻的坐标为

(1)

式中,xi0(i=1,2,…,I)为第i个站在参考历元t0的协议坐标,为未知参数;速度v0为在参考历元t0的协议速度;δPSD为地质灾害引起的非线性部分,如地震的震后形变等。一旦获得各测站的协议坐标和协议速度,无论该测站是否处于工作状态,都可实现该基准站坐标维持。考虑到数值计算需要和大地测量习惯,上述时间单位建议采用年。

为便于讨论,下面仅考虑平面方向时间序列,并暂不考虑测站非线性变化(以E方向为例)。对于第i个海底基准站,假设存在J个历元观测,则可构造以下观测方程

(2)

式中,ε为观测与模型不符值,主要包括观测随机误差、区域构造形变及地震震后形变等影响。等号左侧为观测量,记为L,右侧xi0和ve0为待估量,则式(2)的最小二乘解为

(3)

式中,P为观测权阵;A为观测设计矩阵;1J×1为由1构成的(J×1)维列向量;0J×1为由0构成的(J×1)维列向量。

海底观测时间序列偏离线性运动模式,一般是由地震等地质灾害事件引起的。此时,可考虑采用地震的震后形变模型来构建测站非线性运动。对于高程方向,还应考虑年周期、半年周期等非线性周期性信号[25]。然而,受限于海底定位精度及复测周期,目前海底基准站网还很难实现高程方向时序分析。因此,本文主要考虑海底水平构造运动,并将海底地震等引起的异常当成粗差观测处理。无论是观测异常,还是各种地质灾害引起的时间序列异常,都可使用抗差估计策略予以处理。本文采用以下IGGⅢ抗差估计[26-28]

(4)

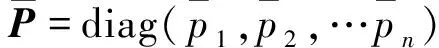
(5)

IGGⅢ方案拥有正常权段、可疑降权段,以及淘汰权段,可充分利用观测数据,具有较强抗差性,其中,k1=1.5,k2=2.5为常用推荐值。

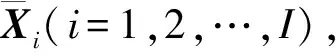
(6)

如图1所示,在旧海底基准网将要供电不足时安装新海底基准网,二者都是局部基准网,共同构成整体基准网。局部基准网中心点之间存在一定的差值。为了确保上述中心点法监测海底地壳运动的连续性,需要通过新旧海底基准网同步观测,得到中心点间的差值Δx,以后历元启动新海底基准站网,并将Δx补偿到新海底基准网中心坐标,即可保证中心点坐标时序的连续性[19]。

图1 更换海底基准站

换站补偿后的中心点法是海底构造监测的一种有效方法,采用重心基准有利于区域构造形变分析,但由于缺少如ITRF控制下的长期基准约束,不利于长期、大尺度海底构造分析。中心点法可以平滑观测噪声,但某个站点异常可被中心点平均化处理削弱而无法对其进行探测和分离,或者因其中少数站点异常,导致整个基准站组视为异常。此外,中心点坐标时序为虚拟观测时序,从而无法获取各站点在协议参考历元处的站坐标估计和站速度。

2 试验结果分析

文献[19]公布了7个观测站在2011—2020年的GNSS-A实测数据,其空间分布如图2所示。本文基于这7个站的观测数据验证本文方法的有效性。

图2 试验区海底基准站分布

2.1 中心点法及换站补偿

中心点法及换站补偿对GNSS-A数据的处理策略见表1,大致分成了3个环节。

表1 数据处理策略

以MYGI站E方向为例说明换站引起的时间序列间断问题。MYGI站在海底有8个基准站,编号分别是:M01、M03、M04、M05、M12、M13、M14、M15,在2011—2020年观测期间发生了3次换站,本文通过开源的GARPOS软件解算得到10年的虚拟中心点数据。中心点坐标如图3所示,不同海底基准站网的中心点之间相差较大。因此换站导致原始海底观测时序无法直接用于海底地壳运动监测。

图3 MYGI站原始中心点时间序列

对虚拟中心点的偏移量时序进行最小二乘拟合,即可得到海底基准网的整体运动趋势和线性速度信息。非线性部分主要代表地壳形变或地震等异常。如图4所示(以E方向为例),可以看到MYGI站整体符合线性运动趋势和地壳整体构造运动特征,其中拟合直线公式为y=vt+dx,v代表局部海底基准网中心点的运动速度,dx是最小二乘拟合得到的坐标改正数,文中所有中心点速度拟合直线均由上述方法绘制。

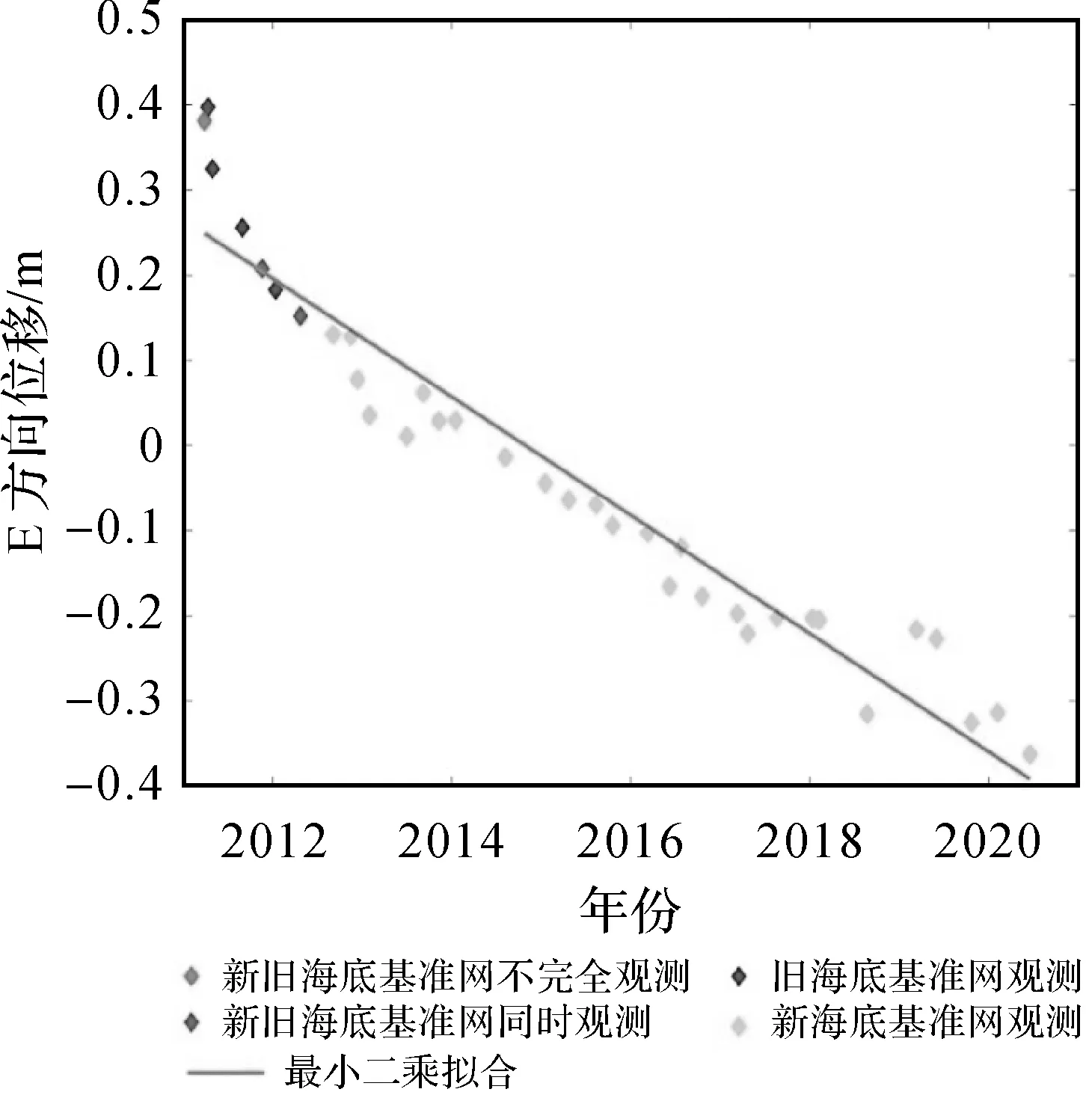
图4 MYGI站中心位移与最小二乘拟合

将新旧海底基准站网中心之间的差值补偿到新海底基准网的中心点上(图5),可以看到补偿之后海底基准站网的中心点时序已具备了海底地壳运动信号提取能力。

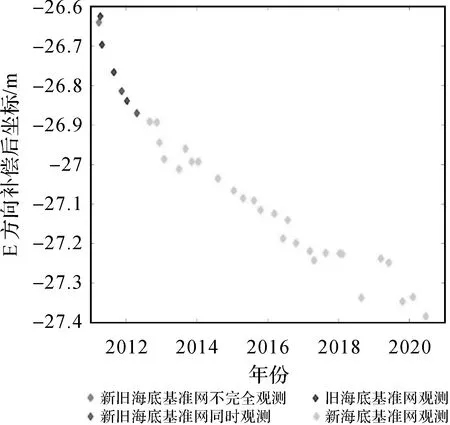
图5 MYGI站补偿中心点时间序列

在使用重心基准前,先基于初始中心点计算海底基准站网的运动速度,正常情况下的运动速度为厘米级。由表1可知,MYGW观测站利用初始中心点计算出来的运动速度过大,与实际不符,即基于初始中心点来研究海底运动一般是无效的。表2给出了重心基准下求得的虚拟中心点运动速度,相对于初始中心点结果更符合地壳运动实际情况。

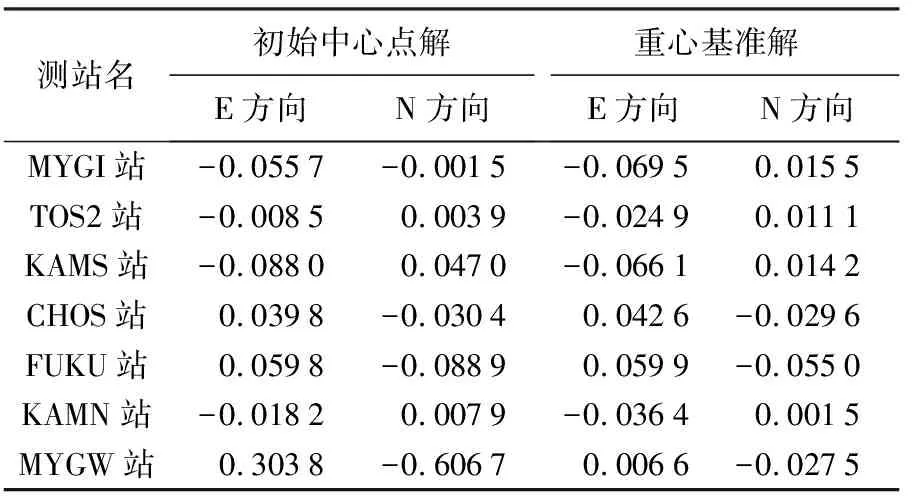
表2 水平方向初始中心解重心基准解的中心速度

2.2 联合估计模型解

下文继续以MYGI站为例,使用本文模型计算整体基准网速度。通过GARPOS软件确定海底坐标,图6中拟合直线公式为y=vt+dx,v代表整体海底基准网运动速度,dx表示最小二乘拟合得到的协议坐标改正数的平均值,文中所有动态平差速度拟合直线均由上述方法绘制。可以看出,受观测异常影响,绝大部分海底基准站位移时序都处于拟合直线的左下侧,这是不合理的,笔者认为这主要是由观测异常引起的。

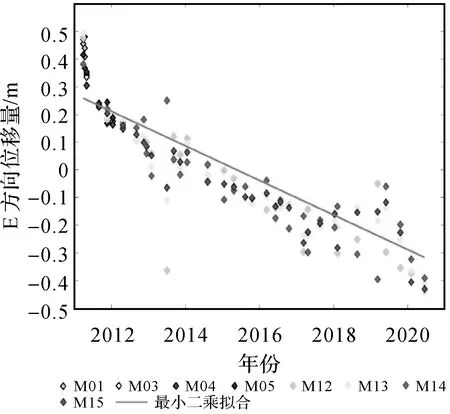
图6 MYGI站海底基准站位移与模型拟合

接下来比较本文联合估计模型解中的站速度与重心基准下中心点速度的差异,比较结果见表3,两种结果之间的差值大多在毫米级。因此,利用联合估计模型计算出来的速度也是有效的。

表3 中心速度与联合估计模型速度

由表3可知,此时水平方向的中心速度与联合估计模型速度之间平均相差5 mm/a左右,相差较大。下文分析速度差值较大的站点。例如,CHOS观测站在E方向上的中心速度与联合估计模型速度相差1.94 cm/a,误差较大。因此,本文着重分析CHOS观测站E方向时序。CHOS站两种方法各自的残差分布情况如图7所示。由图7可知,2011年前几次观测数据的模型残差和中心残差均较大,因此,可认为2011年的观测应视为异常观测。考虑到2011年该区域发生了Mw 9.0级地震,该异常可能是地震的震后形变、黏弹性松弛等原因引起的。此外,在2018年,联合估计模型的残差较大,而中心残差没有明显异常。可以认为联合估计模型对观测异常更为敏感。

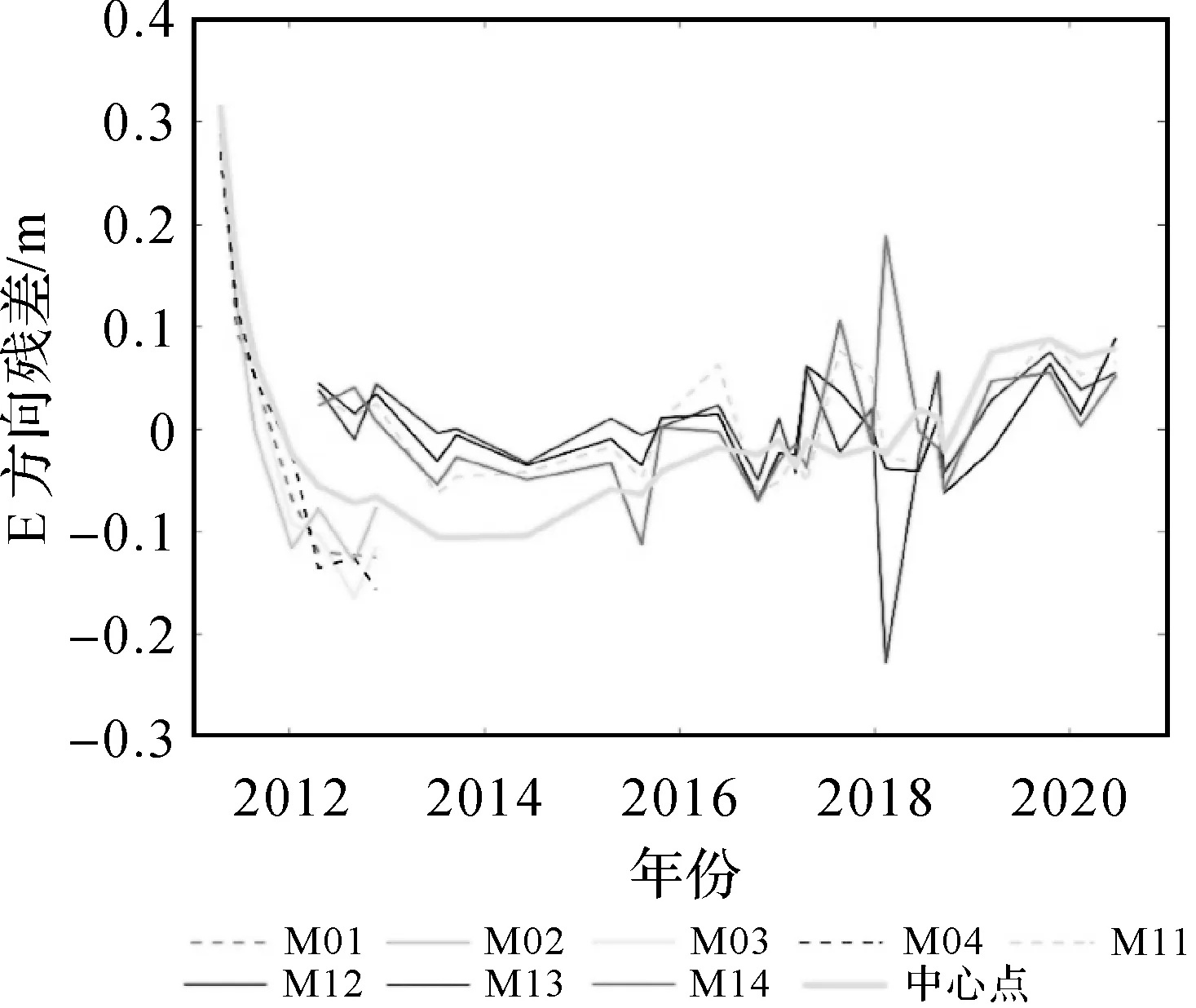
图7 CHOS站模型拟合残差与中心拟合残差比较

为消除异常观测影响,本文采用IGGⅢ抗差估计,即对联合估计模型与中心点法采用相同策略进行抗差估计,结果见表4。

表4 CHOS站E方向抗差前后速度

由表4可知,抗差之后联合估计模型速度与中心速度之间的差值已经减小到了毫米级,且本文方法抗差前后的结果变化也相对较小,说明本文方法更稳健。抗差后两种方法的残差比较如图8所示,说明抗差对联合估计模型与中心点法都有明显的改善作用,经过抗差估计可以把绝大部分残差约束在±0.1 m以内。

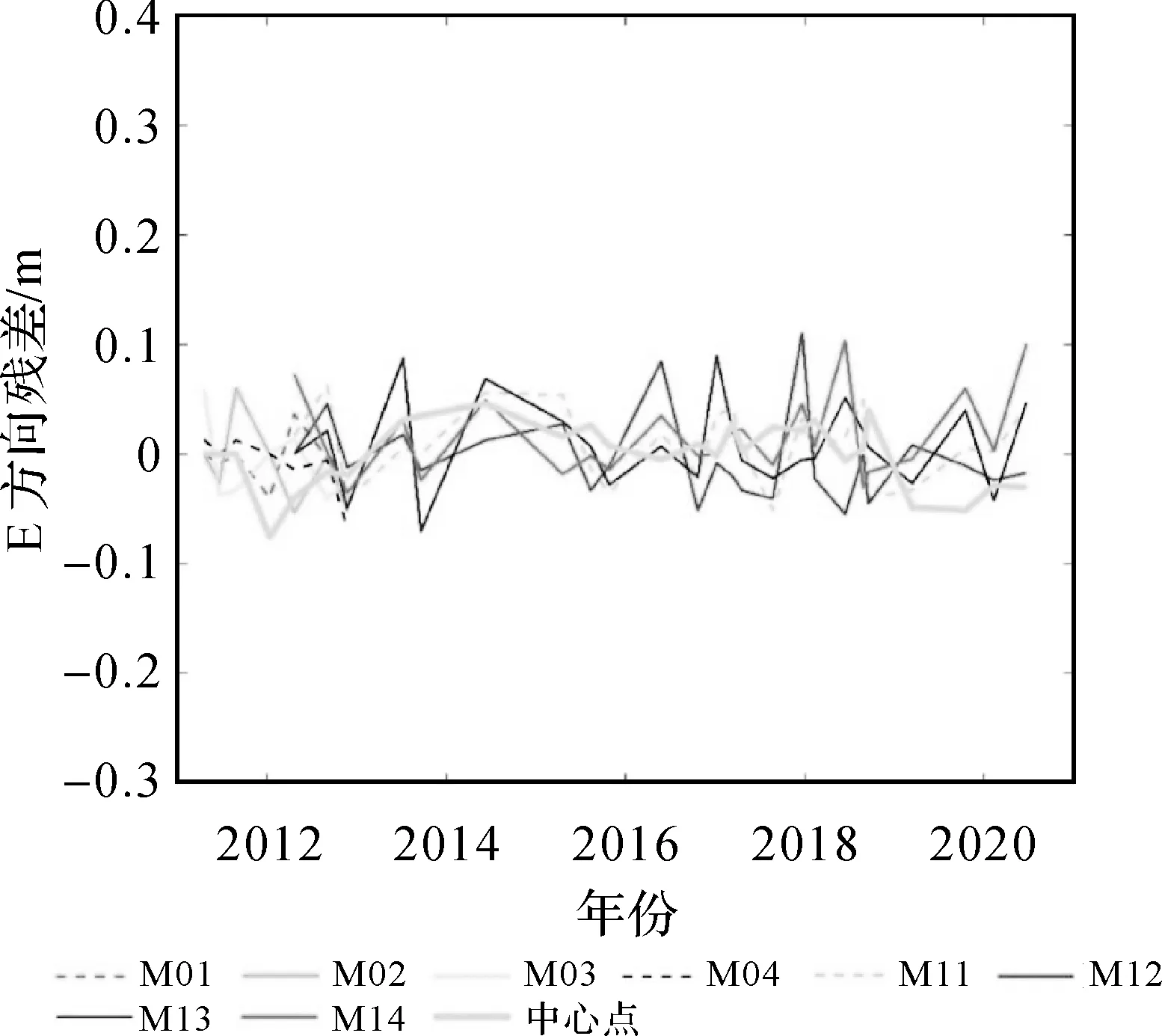
图8 CHOS站抗差后模型拟合残差与中心拟合残差比较

结合图7、图8可以看出,联合估计模型和中心点法在抗差过程中都对2011年的观测数据进行了处理,但本文提出的联合估计模型,可对数据处理进行精细抗差,即可只对单个有问题的海底基准站观测数据进行删除或降权;而中心点法中的抗差估计,则是直接对中心点进行删除或降权,这样处理比较粗略,其对粗差的敏感度不如联合估计模型。具体表现为联合估计模型在抗差过程中可检测到多个历元观测异常,而中心点法则只检测到2011年附近的观测异常。

下文给出所有观测站的抗差估计结果,两种方法的比较见表5。此时联合估计模型的速度估计与中心点法的速度估计之间的绝对差值平均接近3.1 mm/a,有了较大改善。

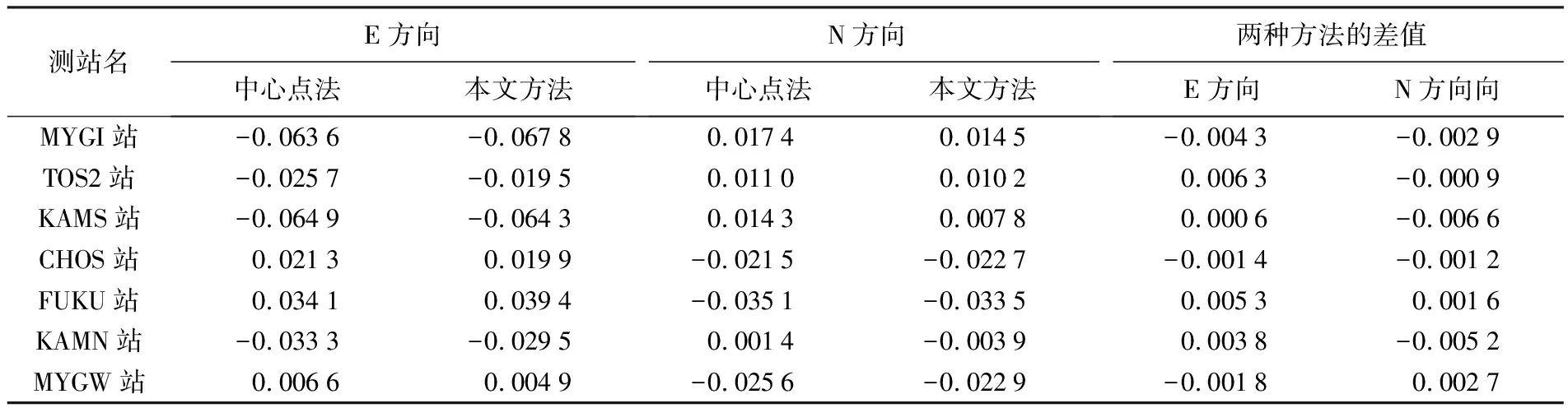
表5 抗差后水平方向两种方法运动速度

为评定中心点法与联合估计模型的结果精度,本文计算了这两种方法进行抗差最小二乘时的标准差(表6)。

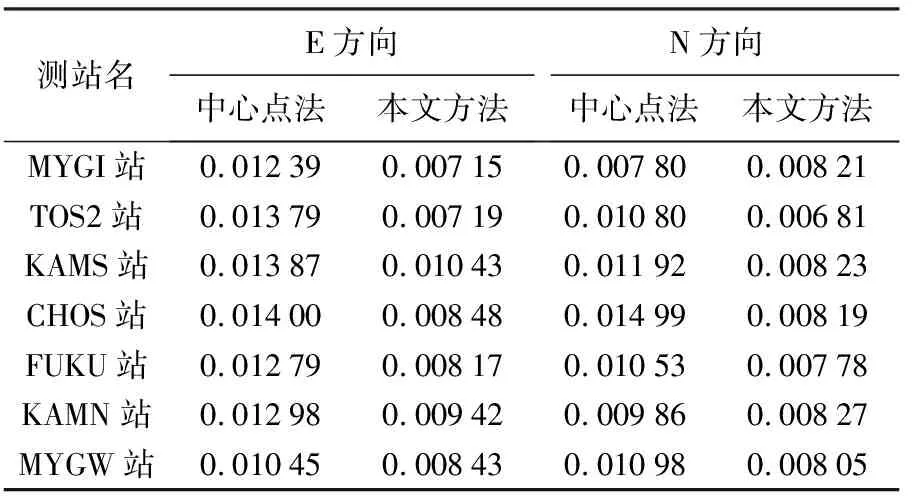
表6 中心点解与动态模型解的标准差

由表6可知,大多数站的联合估计模型标准差小于中心点法标准差,但也存在反常情况。主要是由于中心点法对整组观测进行淘汰或降权,而联合估计模型对数据的处理要更为精细,仅对存在异常的基准站点进行异常观测质量控制。反常发生在MYGI站的N方向,这里中心点法的标准差要小于联合估计模型的标准差,两种方法的最小二乘和抗差最小二乘的速度拟合直线如图9、图10所示。图10中MYGI站在N方向上的海底基准站位移时序较为散乱,其精度相对较低也是合理的。而图9的中心点时序也不稳定,可能是在抗差最小二乘过程中删除较多的观测数据,所以得到的标准差较小。

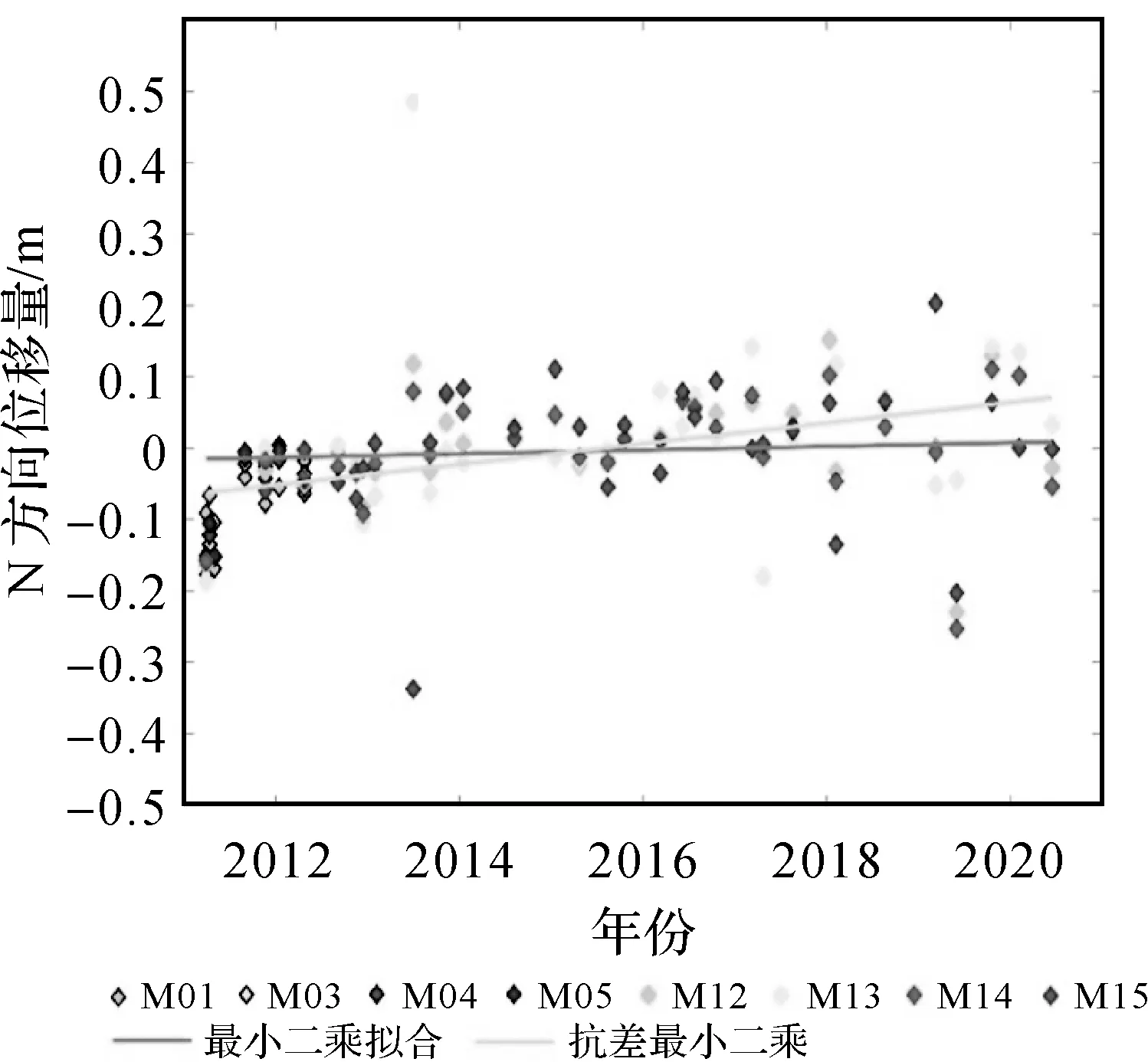
图9 MYGI站的本文方法速度拟合

图10 MYGI站的中心点法速度拟合

图11是所有观测站分别用两种方法计算出来的运动趋势示意图,其中,深色箭头是联合估计模型的运动方向及速度大小,浅色箭头是中心点法的运动方向及速度大小。可以看出,观测站按照运动方向大致分为了两组,分别向两个不同的方向运动。这主要是板块构造引起的,且研究结果和其他学者的研究结果具有很好的一致性。

3 结 论

本文构建的海底基准站网联合估计模型,参考国际地球参考框架(ITRF)建立与维持策略,采用明确的参考历元站坐标与站速度作为未知参数,对海底基准站网时序观测进行动态数据处理。不但可以研究形变问题,还可以获取各站点在协议参考历元的站坐标和站速度,用于导航应用。虽然两种方法所采用的基准和换站处理方法均不同,但计算出来的海底基准站网速度非常接近。中心点法需要在换站情况下新旧两个海底基准站网同时观测来进行中心点补偿,而联合估计模型则不需要新旧基准网联合观测,这对海底基准站网维持的观测要求相对较低。需要指出,在不同观测时期,海底基准站网定位可能采用不同的ITRF参考框架,在海底基准站时序观测数据处理时需要考虑上述参考框架间的差异。

海底地震事件或观测异常可引起海底基准站时序观测出现异常,即出现脱离测站时序线性运动趋势的现象。因此,若要精确估计海底基准站网的线性运动速度,需要对这些异常观测进行质量控制。然而,由于海底基准站网一般每年只能复测2～4次,观测样本数量有限,为此,本文提出抗差最小二乘,有利于改进中心点时序和各测站原始观测时序的处理,且可提高测站速度估计的可靠性。

研究发现,由于日本2011年发生了Mw 9.0级大地震,期间海底基准站时序观测存在明显的观测异常。因此,对于明确地震引起的震后形变,可采用ITRF 2014指数-对数模型予以处理,这也是本文的后续研究内容之一。此外,MYGW站和MYGI站相邻,但存在明显不同的测站运动方向,这意味着该区域存在较为复杂的地质构造运动。