局域重力场球冠谐建模与联邦滤波相结合的重力匹配导航算法
2023-12-15李姗姗李新星宋星光万宏发
黄 炎,李姗姗,李新星,宋星光,范 雕,万宏发
1.军事科学院国防科技创新研究院,北京 100071; 2.信息工程大学地理空间信息学院,河南 郑州 450001; 3.北京航天飞行控制中心,北京 100094
水下潜航器搭载的惯性导航系统(inertial navigation system,INS)因惯性元器件等误差导致的定位误差随时间积累,定位精度逐渐发散。为了抑制惯性导航系统误差发散,同时不造成潜航器隐蔽性能损失,国内外学者对各类校准惯性导航的方法进行了研究,其中利用海洋先验重力场信息进行匹配导航的思想得到了广大学者的认同。各类重力匹配算法中,基于递推估计最优滤波原理的单点迭代匹配算法(尤其是Kalman滤波匹配算法)以其良好的实时性和在低信噪比条件下的高精度特性被广泛研究和应用[1-3]。但是,在采用Kalman滤波方法匹配导航过程中随着重力观测量的增加,若仅采用传统Kalman滤波进行计算,则各类观测量的量测误差会相互影响,降低滤波精度,同时也不方便对量测故障进行诊断。因此,本文采用联邦Kalman滤波(federated Kalman filter,FKF)对多观测量进行分散降权处理,将每一个独立的重力观测量作为一个子系统的观测值,从而避免某个观测量出现粗差时影响整个系统的滤波精度,同时也便于对各个子系统的故障问题进行隔离与诊断。
为保证滤波精度,还需要建立较为准确的子滤波器量测方程,该过程需要对重力量测值及其变化率进行局部建模,而构建模型的精确与否又直接影响滤波结果精度。目前,应用于重力匹配导航的局部重力场构建方法有平面拟合法、双二次曲面法和重力场球谐模型法等[4-6]。其中平面拟合法效率较高,但是仅是线性展开精度难以保证;在此基础上文献[4]使用双二次曲面对局部重力场进行拟合,计算较为高效,但由于展开阶次的限制,恢复重力场的信息仍然不够精细;文献[5]使用傅里叶阶数表示局部重力场的连续解析形式,但该方法会由于添零导致部分区域精度较差,且计算效率不高;文献[6]使用重力场球谐模型计算局部重力场信息,使用并行技术提高计算效率,尽管在阶次方面达到了应用需求,但是对于匹配导航局域性、实时性特点而言,重力场球谐模型计算复杂、耗时长且在局部重力场的精细结构和高频信息的表述上则显得精度不足,尽管通过并行方法可提高其计算效率,但并行计算设备增加了成本和潜航器计算机功耗。
局部重力场的谱方法是地球重力场理论的研究重点,如何构造合适的谱函数并对其进行快速有效计算是核心问题。本文基于局部重力场球冠谐分析(spherical cap harmonic analysis,SCHA)方法,采用海洋重力场先验信息,使用改进球谐分析技术(adjusted spherical harmonic analysis,ASHA)快速构建局部重力场球冠谐模型,并在此基础上组建FKF子滤波器非线性量测方程,实现对潜航器惯性导航系统的误差估计。
1 FKF滤波器构建
联邦Kalman滤波器是一种典型的分散式滤波器[7],由一个参考系统(主滤波器)和若干个子系统(局部滤波器)组成,属于两步级联的分散式滤波系统[8]。根据惯性/重力/重力梯度组合导航原理,其FKF滤波器结构如图1所示。

图1 重力匹配FKF滤波结构
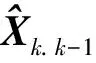
1.1 滤波观测量选取
利用重力和重力梯度信息作为子滤波器观测量进行滤波匹配时,重力异常和扰动重力梯度共有6个独立分量(Δg、Tzz、Txx(或Tyy)、Tzx、Tzy和Txy)。根据适定边值问题理论,Δg和Tzz分量能够反映完整的重力场信息,可以直接作为观测量进行滤波匹配;而Txx(或Tyy)、Tzx、Tzy和Txy则无法单独使用。为此引入复数坐标,根据适定边值问题理论,获得包含完整重力场信息的重力矢量与扰动重力梯度的复数组合形式。
以局部北东天坐标系为基准,定义复数坐标系(i-,i0,i+),则其可用北东天坐标系坐标(X,Y,Z)表示为[9-10]
(1)
因此在复数坐标系下,扰动重力矢量∇T和扰动重力梯度张量∇·∇T可表示为
(2)
式中,T表示扰动位。

1.2 主滤波器状态方程
重力/重力梯度信息对速度误差的反应不够敏感,故在进行重力匹配导航时,仅以位置误差作为状态变量。又由于惯性系统的垂直通道是不稳定的,因此高程信息常使用单独通道进行测量,一般通过测深测潜仪等来改进垂直通道的不稳定性。因此本文选用X=(δφ,δλ)T作为滤波状态变量。由惯性导航误差方程和滤波状态变量可知,惯性导航系统平面定位误差微分方程表达式为[6]
(3)
式中,δφ和δλ分别表示纬向和经向误差;h表示高度;ve表示东向速度;RN表示指示位置点卯酉圈曲率半径;φ表示地心纬度;Wφ与Wλ表示由系统噪声产生的纬向和经向误差。

Xk=Φk/k-1Xk-1+Wk-1
(4)
式中,Xk表示滤波状态向量;Φk/k-1表示状态转移矩阵,可由系统状态矩阵F通过Laplace变换得到Φk/k-1=I+tF,t表示滤波周期。
1.3 子滤波器量测方程
由于重力量测值与状态参数之间呈非线性关系,对于非线性系统常通过构建局部重力场解析函数,获得匹配点重力场值在x和y方向上的变化率,而后利用惯导指示位置在重力基准图上的比对值、潜航器搭载的重力仪测量数据经过计算得到的实际重力值之差及其变化率构建滤波量测方程,如图2所示。
由于地球重力场是一个与位置有关的连续物理场,因此,假设水下潜航器真实位置的重力异常Δg和扰动重力梯度组合在惯导指示位置点(φj,λj)的邻域内存在一阶导数,利用泰勒级数将其展开可得[4]
(5)
式中,vgj、vTzzj、vTzxj与vTzyj表示泰勒级数展开过程中的截断误差;ΔgM(φj,λj)、TzzM(φj,λj)、TzxM(φj,λj)与TzyM(φj,λj)表示利用惯导指示位置坐标在重力异常和扰动重力梯度基准图上提取出的重力异常值和扰动重力梯度值;Δg(φ,λ)、Tzz(φ,λ)、Tzx(φ,λ)与Tzy(φ,λ)则表示水下潜航器真实位置处的重力异常值和扰动重力梯度值。
又因为水下潜航器自身搭载有重力仪和重力梯度仪,因此,Δg(φ,λ)与Tzz(φ,λ)又可表示为[4]
(6)
式中,vgs、vTzzs、vTzxs与vTzys表示由于重力仪和重力梯度仪测量产生的观测误差;Δgs(φj,λj)、Tzzs(φj,λj)、Tzxs(φj,λj)与Tzys(φj,λj)表示由重力仪和重力梯度仪测量并计算得到的重力异常和扰动重力梯度分量观测值。
联合式(5)、式(6)可得到重力异常和扰动重力梯度组合的匹配导航的滤波量测方程分别为
(7)
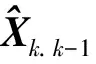
(8)
(9)
式中,Pk.k-1表示一步预测误差方阵;Rk*表示量测噪声方差阵;δ为阈值常数,本文取δ=2.5。
(10)
(11)
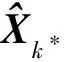
2 基于SCHA建模的局部重力场模型
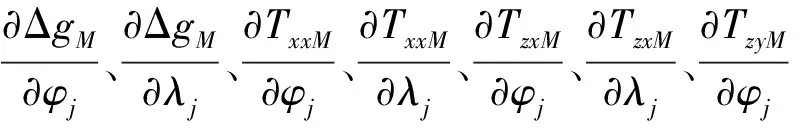
由于采用了多个重力观测量作为不同子滤波器的量测值,因此若直接使用离散格网数据对观测值进行局部建模,则各个观测量需要通过各自数据分别进行建模,计算效率受到损失。当研究区近似一个球冠时,球冠谐函数可以作为该区域的谱函数[17-18]。而使用SCHA建模方法,可以有效利用重力场各个扰动场元量与扰动位之间的泛函关系,仅需要进行一次建模即可,减少整体计算量,提高匹配算法实时性。球冠谐函数相较于球谐函数,球冠谐函数使用非整阶勒让德函数替代整阶勒让德函数,余纬θ的取值范围由[0,π]变化为[0,θ0](θ0表示球冠半角),同时将地球自转轴由北极点沿子午线方向旋转至球冠区域中心点(图3)。由于球冠谐分析建模区域范围较小,因此球冠谐函数可以用较少的位系数反映较高分辨率的重力场信息。例如,为了达到某一分辨率,利用球谐分析(spherical harmonic analysis,SHA)建立全球重力场球谐模型需要使用NOSHA个位系数,而在半角为θ0的球冠区域内使用球冠谐分析建立球冠谐模型仅需使用NSCHA个位系数,NOSHA与NSCHA的关系为[18]
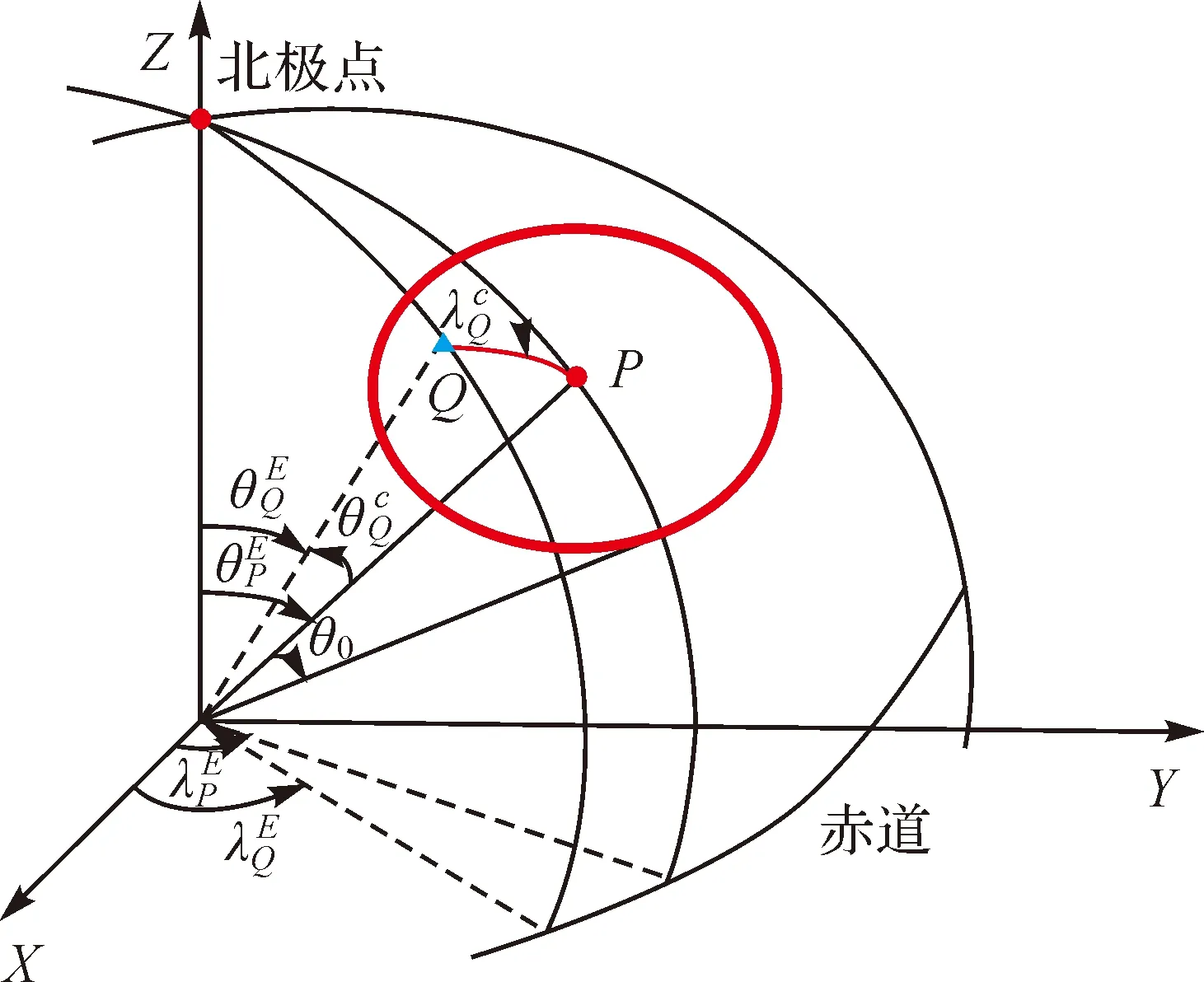
图3 球冠谐坐标系
(12)
式中,Scap表示球冠的表面积;Searth表示地球的表面积。
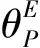
(13)
2.1 广义勒让德函数
扰动位T在球冠坐标系下的级数表达式为
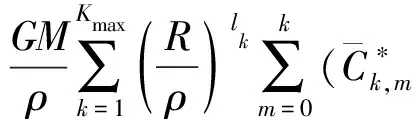
(14)
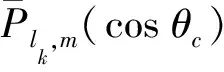
广义勒让德函数是指阶数为实数的勒让德函数,包括整阶、非整阶勒让德函数,直接给出规格化的非整阶勒让的函数计算公式为[18]
(15)
式中,Jmax表示级数的最高阶。Aj(lk,m)可通过递推计算得到,递推公式为[18]
(16)
式中,Klkm表示规格化因子。Klkm近似计算公式为[18]
(17)
2.2 基于移动窗口的球冠谐建模
相对于球谐分析,球冠谐分析建模就是在所选中的某一地球球冠上进行局部球谐分析。根据Helmholtz方程及其边界条件,扰动位在区域内必须要满足一定的边界条件,在球冠极点(即余纬θc=0°)时,球冠谐分析与球谐分析相同;而在球冠边界处(即θc=θ0)时,扰动位需满足以下边界条件[18-19]
(18)
文献[18—19]给出了式(18)的等价形式
(19)
不同的半角θ0与模型级数m对应式(18)的解不同,且lk一般为非整数,因而通过Helmholtz边界条件反解非整阶勒让德函数阶数的计算量较大、耗时较长,不利于重力匹配导航实时性需求。为提高计算效率,引入ASHA技术[20],该技术能够在保证区域模型构建精度的前提下减少计算时间,提高匹配算法实时性(图4)。ASHA技术的核心是将余纬θc由原球冠范围(0,θ0)映射到(0,π/2)上,即映射到半球上,达到将非整阶勒让德函数用整阶勒让德函数进行替换的目的,从而化简勒让德函数的阶数求解过程,减少计算耗时,提高计算效率。

图4 ASHA技术
使用ASHA技术,首先需要对原球冠坐标系的坐标进行转换,将其转换至半球坐标系[20]。具体公式为
(20)
式中,ρ′、λ′、θ′为半球坐标系中的坐标;s表示坐标转换系数。
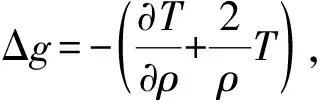
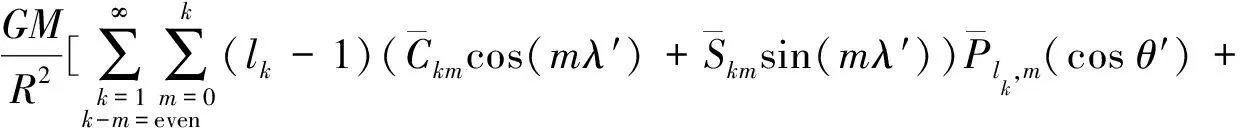
(21)
根据式(21)即可获得球冠谐模型系数与重力异常观测值间的误差方程为
(22)
式中,g表示由DTU18全球重力异常模型获得的观测数据。
依据式(22)的误差方程即可通过最小二乘法构建局部重力场球冠谐模型。当球冠半角θ0≤20°时,ASHA技术均可以相当的精度把球冠域映射到半球上。
在贫困心理学中,研究者们普遍认为导致短视行为的原因是物质资源缺乏对个体的认知和情感层面产生的消极影响。在认知层面,个体会因为经济需要得不到满足而产生压力感和不安全感,产生无法从身边的重要他人获得支持的信念。在情感层面,个体会产生一系列的消极情感,包括焦虑、恐慌、抑郁、自我贬损以及自主性丧失感等等(Fabio & Maree, 2016)。这些因素也会消耗人们大量的心理资源,使个体没有足够的心理资源去处理其他任务,因而失去了为长远打算的能力,表现为短视(Haushofer & Fehr, 2014)。
2.2.2 移动窗口实时球冠谐模型
尽管球冠谐模型可以用较少的模型系数反映区域较为精细的重力场结构,但是随着球冠半角和数据分辨率的增加,对应球冠谐模型的阶数也随之增加。然而,高阶球冠谐模型存在不稳定性,当阶数lk序号k达到110以上时稳定性急速下降[21]。
目前,海洋重力异常和扰动重力梯度数据的分辨率可以达到1′[6],球冠谐模型阶数应与实际数据分辨率相契合,若数据分辨率为fs,则阶数lk的最大序数Kmax可近似计算得到
(23)
通过式(23)易得分辨率为1′,Kmax=110时,球冠谐模型能达到的最大球冠半角θmax约为55′。但是,水下潜器在进行长时间航行时,航行范围往往大于55′[22-24]。因此直接对整个航行区域进行建模不仅建模范围不足,而且随着匹配点远离建模中心,计算精度也会有所损失。为有效解决该问题,本文选择以每一个匹配点为球冠中点,以匹配点附近一定范围区域重力异常作为观测数据,构建以匹配点为中心的小范围高分辨率实时移动窗口球冠谐模型。
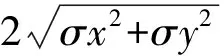
(24)
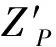
计算得到所有时刻置信概率为P的圆概率误差半径RPi后,整个惯性导航系统的圆概率误差半径RP取RPi中的最大值,即RP=max(RPi)。据此,将两倍的RP作为构建球冠谐模型时的移动窗口最小半径。
3 试验验证与分析
利用惯性/重力/重力梯度组合导航仿真程序进行水下潜航器航迹与测量数据仿真,惯性导航采样率为100 Hz。仿真数据包含惯性元器件输出(角增量与速度增量)、重力异常观测数据、扰动重力梯度观测数据及水下潜航器真实航迹。惯性元器件误差设置见表1。当前,海洋重力仪动态测量精度已达到1 mGal(如德国的KSS系列和美国的L&R系列重力仪),因此重力仪测量误差一般取标准差为1 mGal的白噪声,此外还需要增加一个误差项用以表示由于厄特弗斯改正等因素造成的影响,根据经验取为3 mGal[11]。重力梯度仪的动态测量精度可达到7 E(1 E=10-9/s2)(如美国的HD-AGG和英国的EGG系列重力梯度仪),因此重力梯度仪测量误差取标准差为7 E的白噪声[26]。重力异常基准图选用DTU利用卫星测高数据、实测重力异常数据等反演计算发布的DTU18全球重力异常模型,数据分辨率1′,中误差为2~3 mGal。扰动重力梯度基准图则在EIGEN-6C4地球重力场模型与DTU18全球重力异常模型基础上,基于Stokes理论利用移去-恢复技术计算得到,数据分辨率计算至1′,基于Txx+Tyy+Tzz=0的约束条件,计算结果Txx+Tyy+Tzz绝对值最大值为0.035 E,标准差为0.002 1 E,能够一定程度上反映所构建扰动重力梯度基准图的正确性。同时,由于重力观测量的基准图数据是以格网形式离散存储,导致重力观测量在基准图上的值存在半个格网的等值区域。若量测更新时间较短,则观测值存在强相关性,导致量测方程不可观测;若量测更新时间较长,则惯导累积误差较大难以校正。因此结合本文所用的基准图分辨率及水下潜航器的航行速度,FKF量测方程更新时间间隔选取180 s(即每隔180 s进行一次组合匹配导航校正)。惯导解算采用双子样算法,每次惯导更新均进行一次状态方程更新,因此FKF状态方程更新时间间隔为0.02 s。

表1 惯性元器件误差设置
仿真试验区域大小为2.5°×4°(范围为7°N—9.5°N,110.5°E—114.5°E),试验区重力异常与扰动重力梯度张量基准图如图5所示。

图5 试验区基准
选取5个重力场特征参数,分别为标准差、纬向粗糙度、经向粗糙度、纬向信息熵和经向信息熵[27],用于表达区域重力场分布、描述区域代表性,并作为评价区域适配性的指标。各个重力场分量的特征参数见表2。
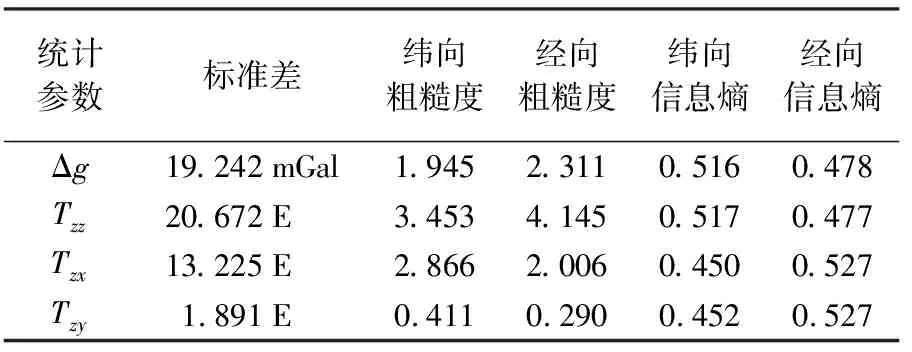
表2 区域重力场特征参数
由表2可知,区域内Δg、Tzz和Tzx的标准差数值较大,而Tzy则由于其自身数值较小,标准差相对较小;各个重力观测量的纬向和经向粗糙度量级相当,表明该区域内各分量纬向和经向的起伏变化相当;各个重力观测量的经向和纬向信息熵均接近0.5(即信息熵极大值),表明该区域各个重力观测量特征变化明显,符合重力匹配导航的应用要求。
试验中,用于匹配导航的航迹(M航迹)航行时长24 h,初始速度(0 m/s,0 m/s,0 m/s),初始姿态为(0°,0°,-10°),起始坐标为(7°N,110°E,-100 m),惯导初始误差设置为1.1 n mile。潜航器首先沿着北偏东45°方向先以0.008 6 m/s2的加速度匀加速至10 n mile/h,然后匀速直线航行12 h;而后右转45°,再匀速航行12 h。
3.1 移动窗口范围选取
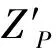
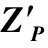
表3 不同置信概率圆概率误差半径与
由表3可知,惯性导航系统置信概率为95%的圆概率误差半径为4.852 n mile,约为5′,因此移动窗口范围最小应选取半角为10′的球冠区域,并以此构建移动窗口球冠谐模型。

表4 误差统计
由表4可知,使用不同移动窗口半径的滤波匹配结果精度近似,但随着球冠半角的增加,相同分辨率对应的阶数序号最大值呈线性增长,球冠谐模型构建耗时则呈指数增加,当球冠半角为20′时,模型构建耗时超过10 s,不利于滤波的实时性计算。因此,在保证精度的前提下,顾及匹配导航实时性需求,移动窗口应选择半径为10′的球冠区域。
3.2 FKF-SCHA重力匹配算法匹配效果分析
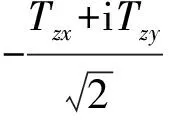

表5 计算耗时统计
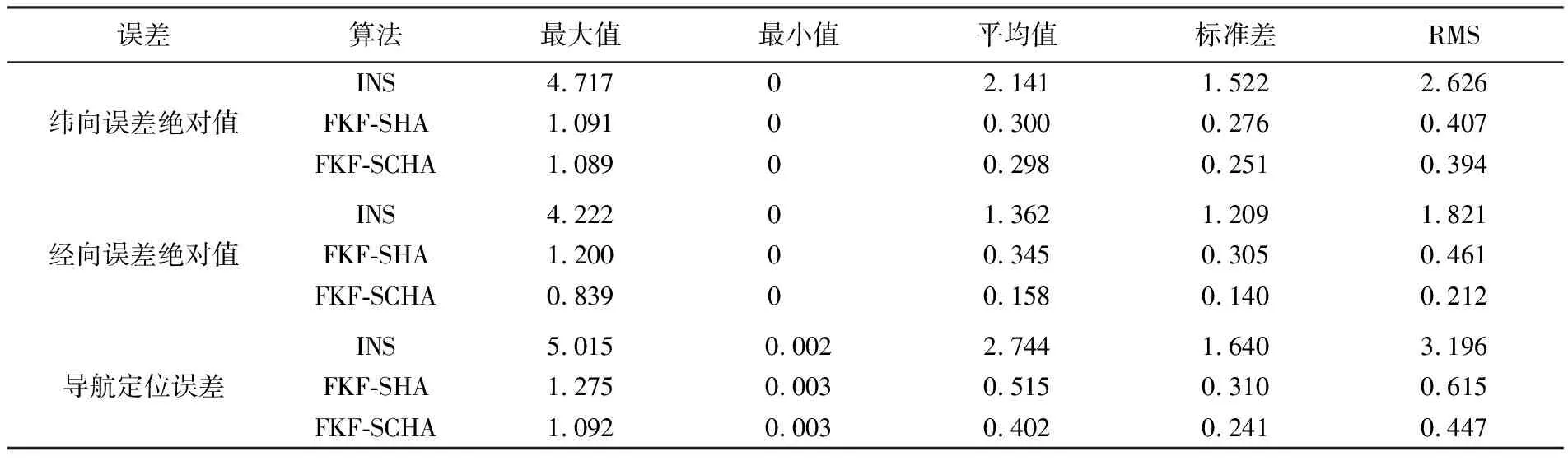
表6 24 h航行误差统计
由以上仿真试验结果可知:
(1) 由表5可知,使用SHA法构建量测方程耗时超过1 s,在使用基于GPU的并行计算方法进行加速后,计算效率得到提高,PSHA法计算耗时为0.090 s,而本文所提移动窗口SCHA法计算耗时与PSHA法计算耗时相当,为0.086 s。但是PSHA法需要使用GPU设备辅助提高计算效率,考虑到潜航器搭载的计算机硬件计算能力和成本,移动窗口SCHA法则更具实用价值。
(2) 结合图6(a)与图6(d)可知,本文所提FKF-SCHA重力匹配算法经过5次量测更新(15 min)即可对初始误差进行修正,且修正后的航迹相较于INS航迹更贴近于参考航迹,说明本文算法是有效的,能够对惯导误差进行一定程度的修正。
(3) 结合表6与图6(b)、(c)可知,惯性导航纬向误差呈周期性变化,经向误差则随航行时间发散;在使用FKF-SCHA重力匹配算法后,纬向误差和经向误差绝对值均值分别为0.298和0.158 n mile。尽管误差曲线存在一定程度的波动,但均是以接近0的均值进行震荡,且误差总体上并未随时间积累,证明重力FKF-SCHA重力匹配算法能够以相当的精度对惯导位置误差进行实时估计并修正。
(4) 结合试验区域重力特征参数与误差曲线,当局部粗糙度较大时,匹配导航效果较优;反之,局部粗糙度较小时,则匹配效果较差。当移动窗口范围内重力观测量信息熵数值在(0.4,0.6)范围内时,匹配效果显著;当移动窗口范围内重力观测量信息熵数值在(0,0.2]∪[0.8,1)时,则匹配效果较差。
(5) 结合表6与图6(d)可知,在24 h航行过程中,INS导航定位误差最大值达到5.015 n mile,平均误差为2.744 n mile。在使用FKF-SCHA重力匹配算法后导航定位误差最大值为1.092 n mile,减少了78.2%;平均误差为0.402 n mile,减少了85.2%;导航定位精度提高了85.3%。相较于FKF-SHA重力匹配算法,FKF-SCHA算法导航定位误差最大值减少了14.4%,平均误差减少了21.9%,导航定位精度提高了22.3%。统计结果表明,重力FKF-SCHA重力匹配算法可以有效减小INS累积误差,提高匹配精度。
3.3 长时间航行仿真试验
为验证FKF-SCHA重力匹配算法在潜航器长时间水下航行时的有效性,在3.2节的仿真试验基础上,进行潜航器长时间航行试验。试验航迹航行时长240 h(10 d),初始速度与姿态分别为(0 m/s,0 m/s,0 m/s)和(0°,0°,0°),起始坐标为(46°S,76°E,-100 m)。试验区域内各个重力观测量纬向和经向信息熵均在(0.45,0.55)区间,表明该区域满足重力匹配导航适配性需求。潜航器首先沿着正北方向以0.008 6 m/s2的加速度,匀加速至速度达到10 n mile/h,随后匀速直线航行50 h;然后左转90°,再匀速航行80 h;最后右转90°,再匀速航行110 h。航迹与误差曲线如图7所示,匹配导航误差统计结果见表7。
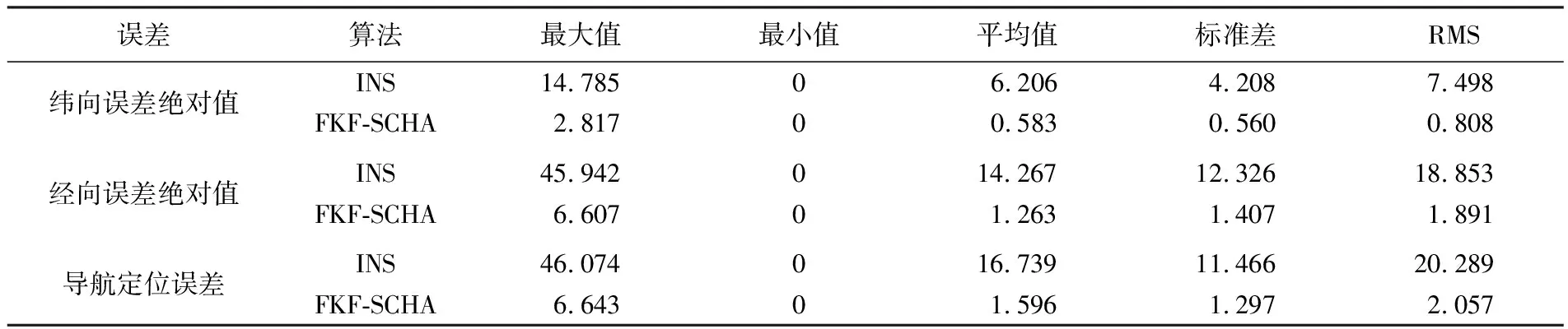
表7 10 d航行误差统计
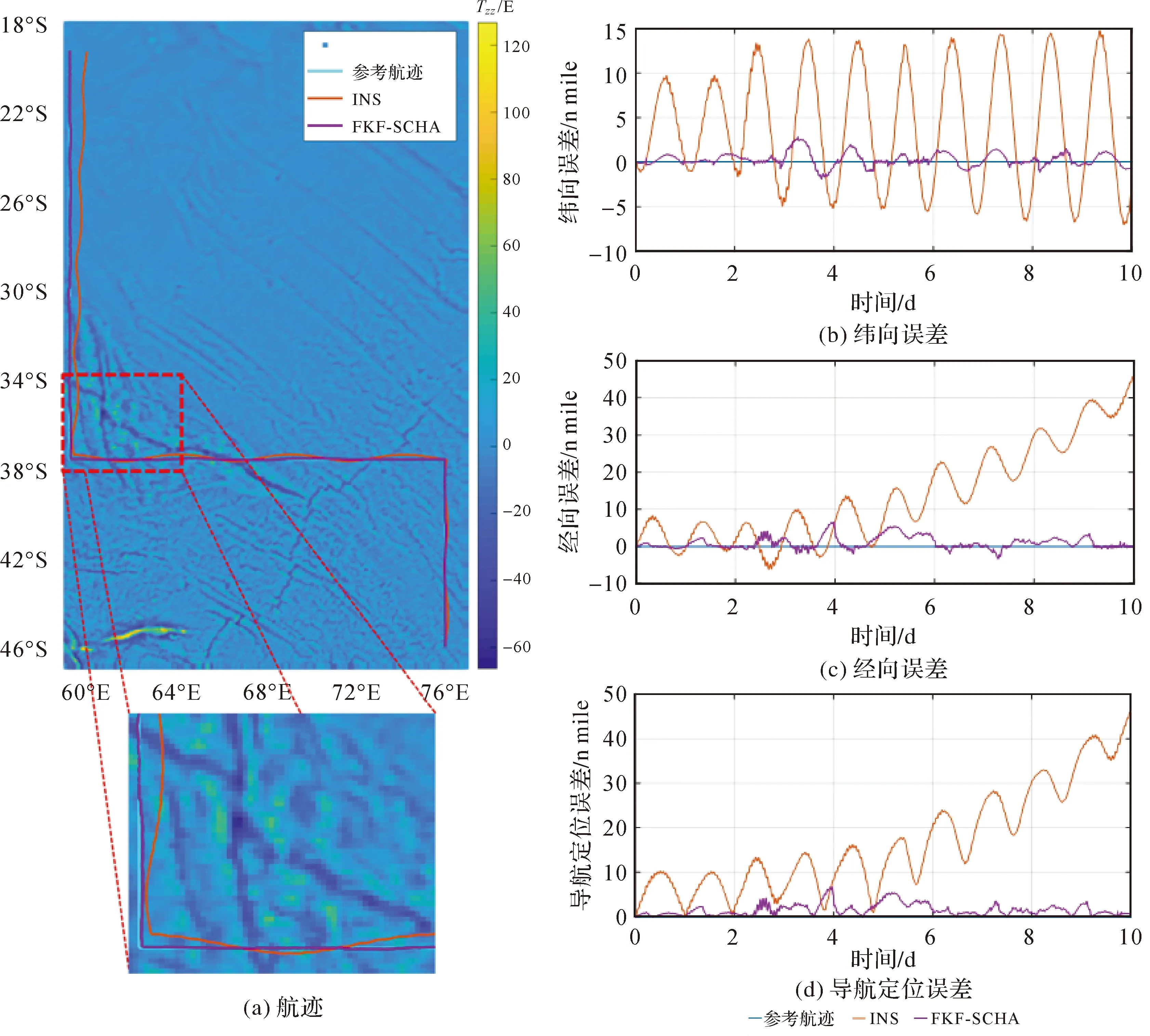
图7 10 d航行航迹与误差曲线
由表7与图7可知,10 d航行过程中,惯性导航系统导航定位误差最大达到46.074 n mile,平均值为16.739 n mile。由于地球自转等周期性误差影响,惯导经向和纬向误差均存在周期性变化,且经向方向存在随时间游走误差。使用FKF-SCHA重力匹配算法后,导航定位误差最大值降低为6.643 n mile,平均值为1.596 n mile,定位精度提高了88.7%。试验结果表明,FKF-SCHA重力匹配算法在潜航器长时间无源导航时能够有效抑制惯性导航系统随时间发散的缺陷,提高系统整体导航定位精度。
4 结 论
本文针对传统重力匹配导航算法各类观测量的量测误差会相互影响而导致滤波精度受损和局部重力场模型构建不准确引起滤波发散的问题,提出了一种基于联邦Kalman滤波和局部重力场球冠谐建模的水下重力匹配导航算法。首先通过FKF滤波器对多观测量进行分散降权处理,同时基于适定边值问题构建FKF子系统滤波器的重力梯度复数组合观测量;然后基于SCHA理论,采用ASHA技术,快速建立以匹配点为中心的移动窗口球冠谐模型,依据该模型将重力量测值表示为连续的解析形式并组建子滤波器非线性量测方程;最后利用预测残差向量设计自适应信息分配因子将各子滤波器状态估值及协方差进行融合得到惯导位置误差最优估计量。试验表明:采用SCHA建模的重力FKF匹配算法在24 h航行过程中导航定位误差保持在1.1 n mile以内,导航定位精度提高了85%以上,并根据水下潜航器长期水下作业航行特性,设计了一组长时间水下无源定位导航试验,试验航行时长10 d,重力FKF-SCHA匹配算法导航定位精度提高了88.7%。试验结果分析表明,重力FKF-SCHA匹配算法能够在一定程度上克服惯性导航系统由于时间推移误差积累的缺陷,提高系统导航定位精度,增加匹配算法的稳健性。
