部分填充混凝土矩形钢管组合桁梁桥冲击系数
2023-12-15刘世忠张锐银郜晋生田智娟栗振锋刘世明毛敏
刘世忠, 张锐银, 郜晋生, 田智娟, 栗振锋*, 刘世明, 毛敏
(1.太原科技大学车辆与交通工程学院, 太原 030024; 2.山西路桥建设集团有限公司, 太原 030006;3.华北水利水电大学土木与交通学院, 郑州 450045; 4.山西省交通科技研发有限公司, 太原 030006)
钢管混凝土组合桁梁、组合桥墩适用于重载、大跨结构,充分发挥了钢管混凝土构件节点承载力高、抗弯刚度大,以及桁架体系受力明确、承载效率高等优势,在国内外工程建设中得到了广泛应用[1-6]。因此,对该类结构进行深入研究具有重要的现实意义。
基于工程设计,刘彬等[7]对混凝土箱梁底、腹板进行优化,提出了矩形钢管混凝土组合桁梁桥这一新型桥梁结构形式,并在中国西部公路桥梁建设中得到应用。刘永健等[8]对实际工程中矩形钢管混凝土组合桁梁桥进行实桥试验,得出在静力荷载系数为1.90~3.05的超载工况下桁梁桥仍然处于弹性工作状态,且主桁下弦杆混凝土填充段与无填充空钢管段所承担静力荷载比例与其轴向刚度比例相吻合。高诣民等[9-10]对矩形钢管混凝土组合桁架进行受弯试验与竖向挠度限值分析,探讨了节点变形对桁架整体变形的影响,后又从耐久性、可维护性等方面论述了矩形钢管混凝土组合桁梁桥良好的服役性能。姜磊等[11-13]引入热点应力法对矩形钢管混凝土组合桁梁桥节点疲劳进行了设计构造优化。综上所述,目前对矩形钢管混凝土组合桁梁桥这一新型结构形式桥梁的研究仅局限在全桥、局部构件与节点的静力、疲劳分析等层面,而有关其冲击系数的研究鲜有报道。桥梁冲击系数是考虑桥梁结构受迫振动放大效应的重要参数,一直是国内外学者与工程技术人员的研究重点[14-20]。Gao等[21]基于现有的车桥相互作用理论,结合ANSYS有限元软件对车桥相互作用问题进行分析,讨论了桥梁结构现有的动态性能设计指标,并提出了公路桥梁在移动车辆荷载作用下的动力性能设计框架。邓露等[22-23]综述了20世纪以来国内外公路桥梁动力冲击系数研究进展,对常见中、小跨径简支梁桥冲击系数的取值进行了较为详细的研究。周勇军等[24]认为设计规范中的冲击系数值不可以直接作为实际桥梁动力性能的评价指标,有必要对不同结构、不同截面的冲击系数分别进行讨论。此外,国内在役桥梁冲击系数设计取值仅停留在规范层面,且中国现行公路桥规《公路桥涵设计通用规范》(JTG D60—2015)[25]在计算桥梁冲击系数时考虑因素单一,故有必要对部分填充混凝土矩形钢管组合桁梁桥冲击系数的影响因素及设计取值进行深入探讨。
陈代海等[26]对比研究了公路桥梁整体法与分离法2种车桥耦合振动分析方法的差异性与优缺点。现基于分离法[27]进行研究,以3跨连续部分填充混凝土矩形钢管组合桁梁桥为工程依托,采用ANSYS有限元软件APDL语言编制部分填充混凝土矩形钢管组合桁梁桥与两轴半简化车辆的车桥耦合系统分析命令流,通过ANSYS瞬态分析功能求得桁梁桥动、静力响应,利用定义法求得桁梁桥关键截面挠度冲击系数与轴力冲击系数。对比分析不同车速、桥面不平度、车重、填充系数等因素对矩形钢管组合桁梁桥冲击系数的影响,通过数理统计给出95%保证率下该部分填充混凝土矩形钢管组合桁梁桥冲击系数参考值。
1 车桥耦合数值仿真
1.1 工程背景
3跨连续部分填充混凝土矩形钢管组合桁梁桥,主桁架长88 m,高2.5 m,共22个节间,截面形式为空间四边形。其中,主桁下弦杆边支点附近2.5 m及中支点附近13 m处填充C50微膨胀混凝土,定义混凝土填充系数为
λ=(L1+L2)/L
(1)
式(1)中:L1、L2分别为桁梁桥主桁下弦杆边支点、中支点附近填充段长度;L为主桁长度;λ为混凝土填充系数,0≤λ≤1。桥梁总体布置如图1所示。

图1 桥梁总体布置图Fig.1 General layout of the bridge
1.2 ANSYS仿真模型
采用基于ANSYS有限元软件平台的 APDL语言建立部分填充混凝土矩形钢管组合桁梁桥与两轴半车有限元模型。其中,采用BEAM188梁单元拟合桁梁桥主桁架杆件、桥墩杆件,采用SHELL181壳单元拟合桥面板,桁梁桥墩底与大地固结(自由度ux=uy=uz= 0);车辆采用两轴平面简化模型如图2所示,车轮与悬架、车身采用MASS21质量单元模拟,悬架、车轮的弹簧阻尼特性采用COMBIN14弹簧单元模拟。车桥耦合系统ANSYS有限元模型如图3所示。车辆技术参数如表1所示。

表1 车辆技术参数Table 1 Vehicle technical parameters

图2 车辆模型示意图Fig.2 Diagram of vehicle model
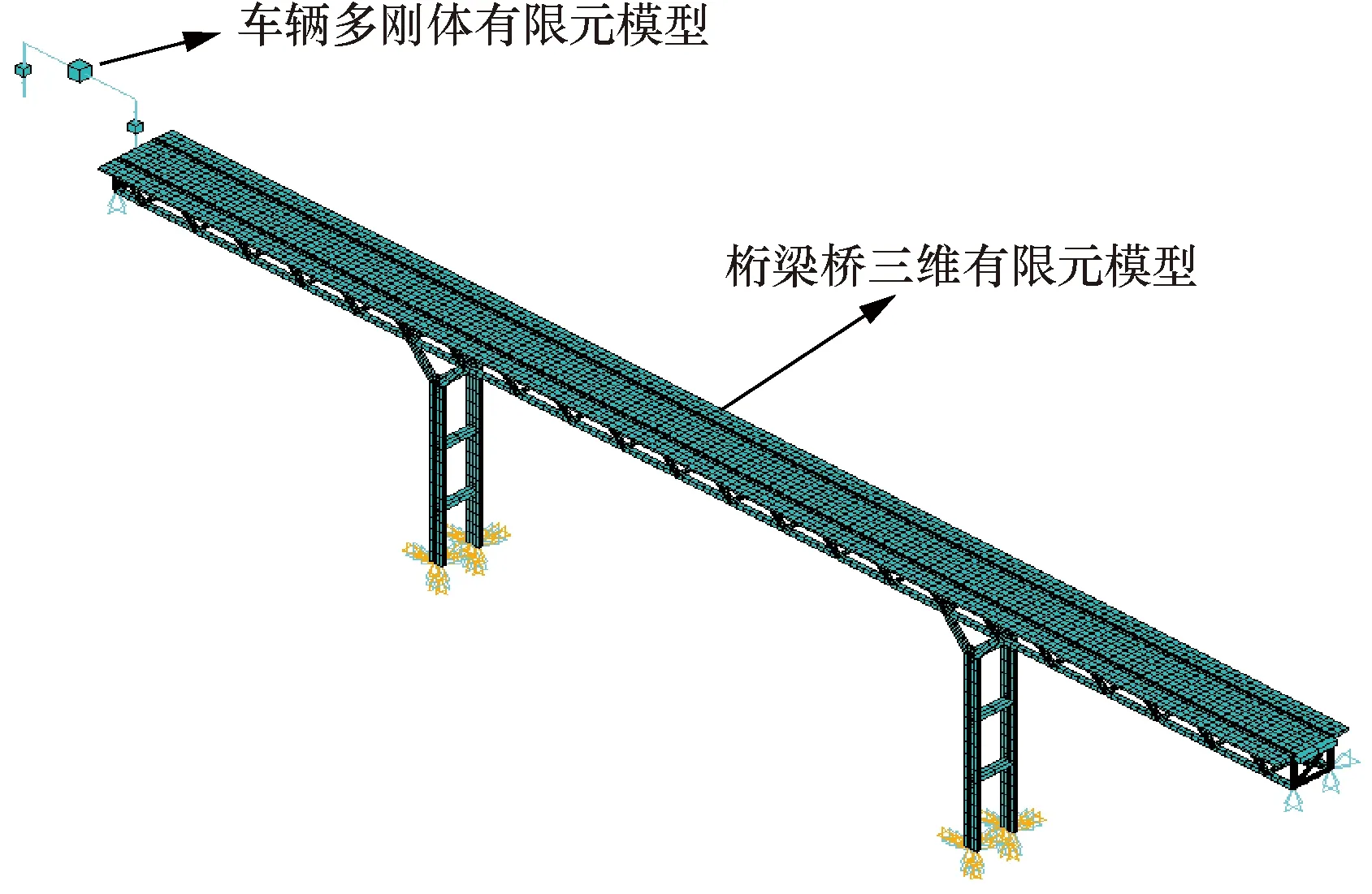
图3 ANSYS车桥耦合系统有限元模型Fig.3 ANSYS finite element model of vehicle-bridge coupling system
基于分离法进行车桥振动求解,该方法[26-27]无需推导矩阵方程与公式,通过ANSYS约束方程实现任意时刻车轮与桥面接触点处位移协调(施加车对桥梁的竖向激励),操作简单,便于推广与工程技术人员掌握。具体求解流程如图4所示。

图4 车桥耦合振动数值求解流程图Fig.4 Flow chart of numerical solution of vehicle-bridge coupling vibration
1.3 桥面不平度模型
结合我国现行《机械振动 道路路面谱测量数据报告》(GB/T 7031—2005)[28],采用数值方法获得A~D共4级桥面不平度统计样本。其中,在桥面不平度数值拟合过程中,功率谱函数需要经过两次变换才可得到最终使用的桥面不平度样本,导致每次计算所得样本都在发生满足一定统计特性的变化。为减小桥面不平度拟合随机过程对计算结果的影响,故采用MATLAB自编程序平行运行10次,获得10组A~D共4级桥面不平度统计样本,取其均值作为部分填充混凝土矩形钢管组合桁梁桥与两轴半车车桥系统竖向位移耦合值,对矩形钢管组合桁梁桥冲击系数进行研究。桥面不平度样本值如图5所示。

图5 桥面不平度样本值Fig.5 Sample values of bridge deck roughness
1.4 矩形钢管组合桁梁桥车激振动响应分析
《公路桥涵设计通用规范》(JTG D60—2015)[25]没有明确规定采用何种桥梁响应进行动力冲击系数计算,邓露等[23]研究表明一般情况下单个车辆作用工况下的桥梁冲击系数较多车同时作用工况下的冲击系数大,且轻质量的车易引起更大的冲击系数。故基于保守考虑,采用单个车辆作用下桁梁桥的冲击系数作为代表进行分析。以桁梁桥初始位置为坐标原点进行桥梁动力响应分析,设桥面不平度等级为A级,假定车轮与桥面始终密贴(不考虑跳车影响),车速为60 km/h,2种钢管混凝土组合桁梁桥在车辆通过时,主桁架下弦杆各截面竖向位移时程与轴力时程三维曲线分别如图6与图7所示。由图6与图7可知,部分填充混凝土能有效降低矩形钢管组合桁梁桥下弦杆的动力响应(竖向位移最大值由-31.77 mm降低至-29.29 mm,轴力最大值由1 436.24 kN降低至1 317.59 kN),但是并没有改变桁梁桥响应时程曲线形状,且对响应最大值发生位置影响很小,响应最大值均发生在中跨跨中。

图6 2种钢管混凝土组合桁梁桥主桁下弦杆竖向位移时程Fig.6 Vertical displacement time history of lower chords of main truss for two kinds of truss bridge
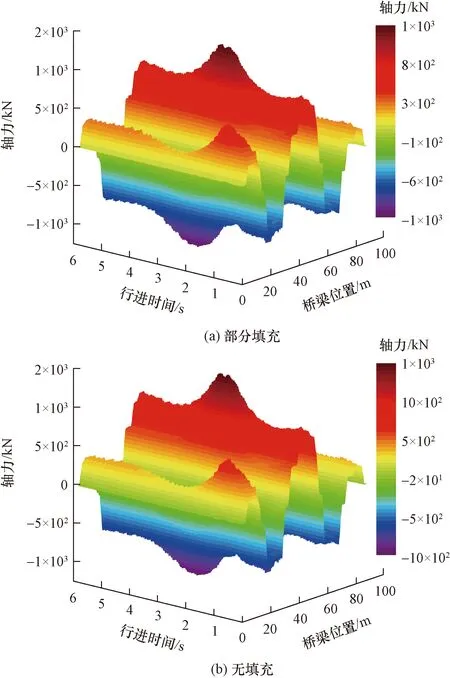
图7 2种钢管混凝土组合桁梁桥主桁下弦杆轴力时程Fig.7 Axial force time history of lower chords of main truss for two kinds of truss bridge
2 参数分析
2.1 矩形钢管混凝土组合桁梁桥冲击系数计算
为探讨车速、桥面不平度、车重等因素对部分填充混凝土矩形钢管组合桁梁桥冲击系数的影响,考虑多个因素,采用桥梁冲击系数定义进行桁梁桥挠度冲击系数与轴力冲击系数计算。桥梁冲击系数μ通常定义为

(2)
式(2)中:Rdy与Rst分别为桁梁桥在移动荷载作用下扣除自重影响的任意截面动、静时程响应最大值。部分填充混凝土与无填充矩形钢管组合桁梁桥冲击系数具体参数分析范围如表2所示。

表2 矩形钢管混凝土组合桁梁桥冲击系数参数分析范围Table 2 Influence parameters range of impact coefficient of concrete-filled rectangular steel tubular composite truss bridge
2.2 车速影响
设2种矩形钢管组合桁梁桥桥面不平度等级为A级,车重为385 kN,计算5种速度下矩形钢管组合桁梁桥冲击系数。车速对两种桁梁桥关键截面挠度冲击系数与轴力冲击系数影响如图8所示。

图8 不同车速下2种钢管混凝土组合桁梁桥关键截面冲击系数Fig.8 The impact coefficients of key sections for tow kinds of truss bridge under different vehicle speed
由图8可知,随着车速增加,两种矩形钢管组合桁梁桥关键截面挠度冲击系数与轴力冲击系数变化趋势并不相同,对应关键截面轴力冲击系数大于挠度冲击系数。当车速从40 km/h增加到100 km/h时,两种桁梁桥中跨跨中挠度冲击系数均低于边跨跨中挠度冲击系数(轴力冲击系数具有相同规律),但冲击系数变化趋势无明显规律,当车速继续增加时,各关键截面冲击系数值很难预测。由此可见,车速对两种桁梁桥冲击系数的影响规律不可预测,部分填充混凝土没有降低矩形钢管组合桁梁桥在移动荷载作用下的动力放大效应。
2.3 桥面不平度影响
设定车速60 km/h,车重385 kN,计算3级桥面不平度等级下部分填充与无填充矩形钢管组合桁梁桥冲击系数,计算结果如表3与表4所示。

表3 不同桥面不平度等级下部分填充混凝土矩形钢管组合桁梁桥关键截面冲击系数Table 3 Impact coefficients of key sections of partially concrete-filled rectangular steel tubular composite truss bridge under different deck roughness grade

表4 不同桥面不平度等级下无填充混凝土矩形钢管组合桁梁桥关键截面冲击系数Table 4 Impact coefficients of key sections of rectangular hollow steel tubular composite truss bridge under different deck roughness grade
由表3与表4可知,随着桥面不平度等级降低,两种矩形钢管组合桁梁桥关键截面挠度冲击系数与轴力冲击系数显著增大,增幅最大约为400%,最小约为116.67%;各级桥面不平度下,两种矩形钢管组合桁梁桥轴力冲击系数最大达到0.44,且明显大于挠度冲击系数;桥面不平度劣化会导致两种桁梁桥在移动荷载作用下的动力放大效应显著增大;部分填充混凝土矩形钢管组合桁梁桥相对于无填充矩形钢管组合桁梁桥关键截面冲击系数未出现差异性规律。
2.4 车重影响
设定桥面不平度A级,车速为60 km/h,计算两种矩形钢管组合桁梁桥在车重变化下的冲击系数,结果如表5与表6所示。
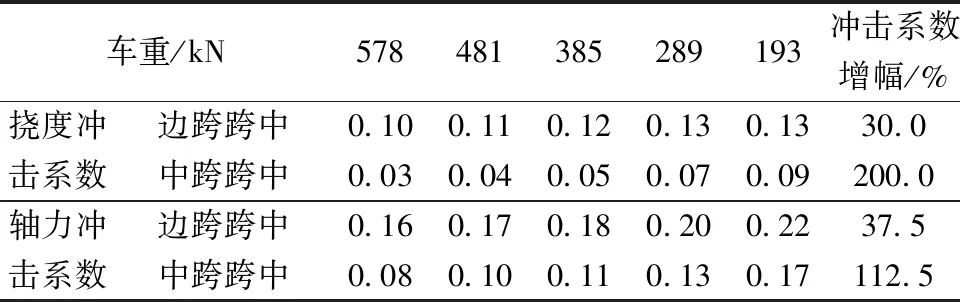
表5 不同车重下部分填充混凝土矩形钢管组合桁梁桥关键截面冲击系数Table 5 Impact coefficients of key sections of partially concrete-filled rectangular steel tubular composite truss bridge under different vehicle weight

表6 不同车重下无填充矩形钢管组合桁梁桥关键截面冲击系数Table 6 Impact coefficients of key sections of rectangular hollow steel tubular composite truss bridge under different vehicle weight
由表5与表6可知,两种矩形钢管组合桁梁桥冲击系数值均随着车重降低而增大,增幅最大约为200%,最小约为30%;两种桁梁桥关键截面轴力冲击系数大于挠度冲击系数。可见,轻车更易引起桥梁较大的动力放大效应,且在进行该类桥梁动力设计时,不可以简单选用挠度冲击系数或轴力冲击系数作为设计值。
3 结果分析
通过对部分填充混凝土矩形钢管组合桁梁桥与无填充矩形钢管组合桁梁桥关键截面冲击系数进行分析,可以看出两种桁梁桥冲击系数无明显规律,但是轴力冲击系数明显大于挠度冲击系数。为进一步确定矩形钢管组合桁梁桥冲击系数与其自身填充系数之间的关系,合理给出此类桥梁动力评价参考,现设定桥面不平度A级,车重385 kN,车速为60 km/h,取9种填充系数对矩形钢管组合桁梁桥进行模态分析与瞬态动力分析,并结合现行公路桥规[25]进行探讨。
《公路桥涵设计通用规范》(JTG D60—2015)[25]对冲击系数的计算与取值描述为
(3)
式(3)中:f为结构基频,Hz。
9种填充系数下桁梁桥冲击系数规范计算值如表7所示,9种填充系数下桁梁桥各截面冲击系数计算值如图7所示。

表7 9种混凝土填充系数下矩形钢管混凝土组合桁梁桥冲击系数规范计算值Table 7 The standard calculation values of impact coefficients of rectangular steel tubular composite truss bridge under 9 concrete filling coefficients
由表7可知,随着填充系数增加,矩形钢管组合桁梁桥基频与其冲击系数规范计算值均在增大,但增幅并不明显,冲击系数规范计算值在[0.19, 0.21]区间内。由图9可知,随着混凝土填充系数的增大(下弦杆混凝土填充长度增加),由于桁梁桥下弦杆相对刚度提高,其冲击系数值略有增大。不同填充系数下挠度冲击系数中支点处较大,跨中处较小;轴力冲击系数边支点处较大,跨中处较小。其主要是由于跨中处相对刚度偏低所致,与桥梁结构的整体刚度分布有关。除中支点与边支点所在截面外,矩形钢管组合桁梁桥其他各截面冲击系数均在一定范围内浮动。其中,中支点处挠度冲击系数值较大,最大值为1.41,边支点处轴力冲击系数值较大,最大值为3.91,远大于其他截面。边支点处弦杆轴力(值)水平很低,桁梁桥设计时由跨中弦杆轴力控制,边跨梁端高轴力冲击系数取值不能反映全桥整体冲击效应。同理由于桥墩的支撑作用中支点处挠度值很小,中支点处高挠度冲击系数也不能反映桁梁桥整体冲击效应。

图9 9种混凝土填充系数矩形钢管混凝土组合桁梁桥冲击系数计算值Fig.9 The calculation value of impact coefficients of rectangular steel tubular composite truss bridge under 9 concrete filling coefficients
基于上述各参数下矩形钢管组合桁梁桥冲击系数计算值,考虑美国、加拿大、中国等国家桥梁规范对某桥梁冲击系数的取值,剔除靠近边支点和中支点处冲击系数大于0.5的样本值,对共867个冲击系数计算值进行拟合优度检验,冲击系数频数统计区间长度取0.05,统计分析结果如图10与表8所示。

表8 冲击系数统计参数表Table 8 Statistical parameters of impact coefficients
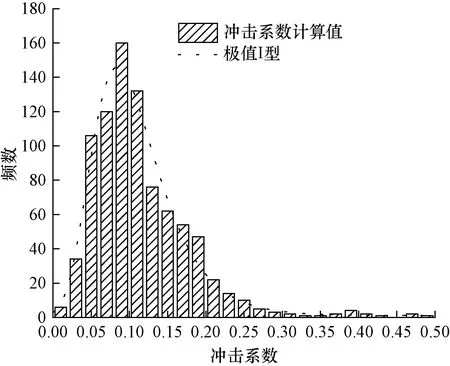
图10 冲击系数频数分布图Fig.10 Frequency distribution of impact coefficients
由图10与表8可知,矩形钢管组合桁梁桥867个冲击系数拟合结果服从极值I型分布,且拟合度较高。在实践中,通常取保证率为95%的参数统计值作为参考值,多因素影响下该部分填充混凝土矩形钢管组合桁梁桥冲击系数对应95%保证率下的数理统计值为0.223。
9种混凝土填充系数下5个国家规范的冲击系数值对比见图11。在所讨论的工况中,美国、加拿大、英国和澳大利亚规范中的冲击系数值均为定值[22-23],分别为0.33、0.3、0.25和0.3,明显高于建议值0.223。对于这种新型桥梁,这些国家规范中的冲击系数取值偏于保守。《公路桥涵设计通用规范》(JTG D60—2015)中冲击系数的取值与桥梁基频[25]有关,随着混凝土填充系数的增大,其值略有增大,如表7所示。基于《公路桥涵设计通用规范》(JTG D60—2015),9种混凝土填充系数下桥梁的冲击系数值均小于建议值0.223,应引起桥梁设计者的重视。
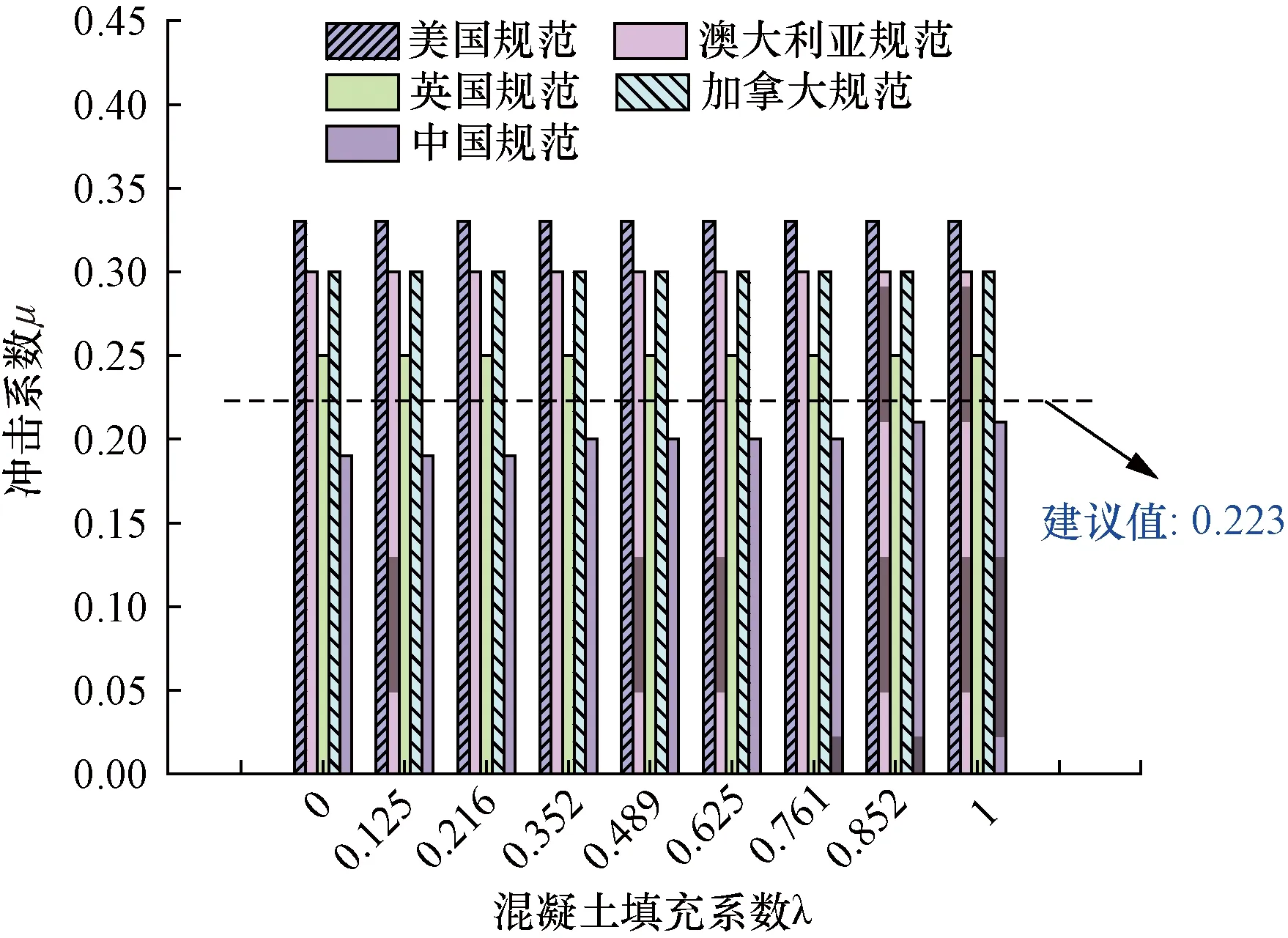
图11 5个国家规范在9种混凝土填充系数下的冲击系数值对比Fig.11 Comparison of impact coefficient values of five national codes under 9 concrete filling coefficients
4 结论
(1)部分填充混凝土后能有效降低矩形钢管组合桁梁桥下弦杆的动力响应,但并没有降低桁梁桥在移动荷载作用下的动力放大效应,各截面冲击系数随混凝土填充系数变化无明显规律。
(2)随着车速增加,部分填充混凝土桁梁桥与无填充桁梁桥关键截面挠度冲击系数与轴力冲击系数变化趋势基本一致,但车速对两种桁梁桥冲击系数的影响规律不可预测。
(3)桥面不平度是影响桁梁桥冲击系数的重要因素,桁梁桥关键截面冲击系数随桥面恶化而显著增大,增幅最大约为400%,最小约为116.67%,可见,在桥梁运营期内定期养护桥面是非常必要的。
(4)桁梁桥冲击系数随着车重降低而增大,增幅最大约为200%,最小约为30%;轻车更易引起桁梁桥较大的冲击系数,但由于轻车的静载效应较小,桁梁桥实际应力水平并不高。
(5)随着混凝土填充系数的增大(下弦杆混凝土填充长度增加),由于桁梁桥下弦杆相对刚度提高,其冲击系数值略有增大。桁梁桥轴力冲击系数显著大于挠度冲击系数,在进行该类桥梁动力设计时,不可以简单选用挠度冲击系数或轴力冲击系数作为设计值。对9种混凝土填充系数下矩形钢管组合桁梁桥冲击系数的867个计算值进行拟合优度检验,拟合结果呈极值Ⅰ型分布,在95%的保证率下,桁梁桥冲击系数建议值为0.223。
