复杂载荷下硬涂层对整体叶盘的减振特性

2023-12-15党鹏飞周哲杨铮鑫龚斌

科学技术与工程 2023年33期

党鹏飞, 周哲, 杨铮鑫, 龚斌

(沈阳化工大学机械与动力工程学院, 沈阳 110142)

整体叶盘是把发动机转子的叶片和轮盘设计成一个整体,采用整体加工或焊接方法制造而成[1]。而在航空发动机中,叶盘结构振动特性对整体结构的可靠性具有很大影响[2]。因此,为了避免整体叶盘在复杂载荷下出现振动性破坏导致结构失效,研究其振动特性是有必要的。

高俊男等[3]为了在整体叶盘结构上有效实施硬涂层阻尼减振技术,以简化整体叶盘为对象并基于Mindlin板理论,建立叶片双面涂敷NiCrAlCoY+YSZ硬涂层整体叶盘的有限元模型,并给出求解涂层整体叶盘固有特性和在阶次激励作用下的频域振动响应的方法。赵宇等[4]基于多点激励单点响应方法开展了整体叶盘结构模型的模态试验,并在多功能转子实验台上开展不同转速下应力测试,验证了其不同转速下的应力分布规律。吴斌等[5]研究发现了某发动机整体叶盘盘体约束状态的变化对叶片模态参数的影响甚微,并且当整体叶盘盘体刚度比叶片大到一定倍数时,叶片的模态即可认为是相对独立的。Mahmoodi等[6]利用确定的接触模型参数,研究了两种涡轮叶片模型的频率响应,并考察了接触面物理性质的抬升现象对涡轮叶片频率响应函数的影响,并展示了其对涡轮叶片振动响应的影响。高峰等[7]提出一种对叶片涂敷硬涂层的阻尼减振方法,并创建了涂敷硬涂层的整体叶盘复合结构连续参数模型,研究得出NiCoCrAlY+YSZ硬涂层会引起整体叶盘固有频的变化。Tang等[8]采用混合维数有限元方法对某整体叶盘进行了振动特性分析。Chen等[9]建立了一种带有硬涂层的整体叶盘自由振动特性和阻尼效应的解析方法,并分析了涂层厚度对固有频率变化和阻尼能力的影响。

现选用钛合金作为整体叶盘的材料,对叶盘叶片的侧面涂敷NiCoCrAIY+YSZ硬涂层,基于ANSYS Workbench模态分析法进行求解。分析在离心载荷、温度载荷、气动载荷耦合作用下对涂敷硬涂层的整体叶盘固有频率的影响;选取具有特征性的振型进行分析总结;分析在激励作用下有无涂敷硬涂层整体叶盘的位移响应;通过绘制有无涂敷硬涂层整体叶盘坎贝尔图,分析在工况转速下硬涂层对整体叶盘的共振影响。

1 有限元建模和材料参数

1.1 整体叶盘有限元模型

首先使用SolidWorks软件对整体叶盘进行三维建模,之后导入ANSYS Geometry中进行模型处理。叶盘整体都采用四面体单元进行网格划分,其中叶片部分网格单位设为5 mm进行加密处理,其余部分设为10 mm,计算共有112 553个单元格和205 003个节点,其整体叶盘模型如图1所示。表1为硬涂层整体叶盘的几何和材料参数。

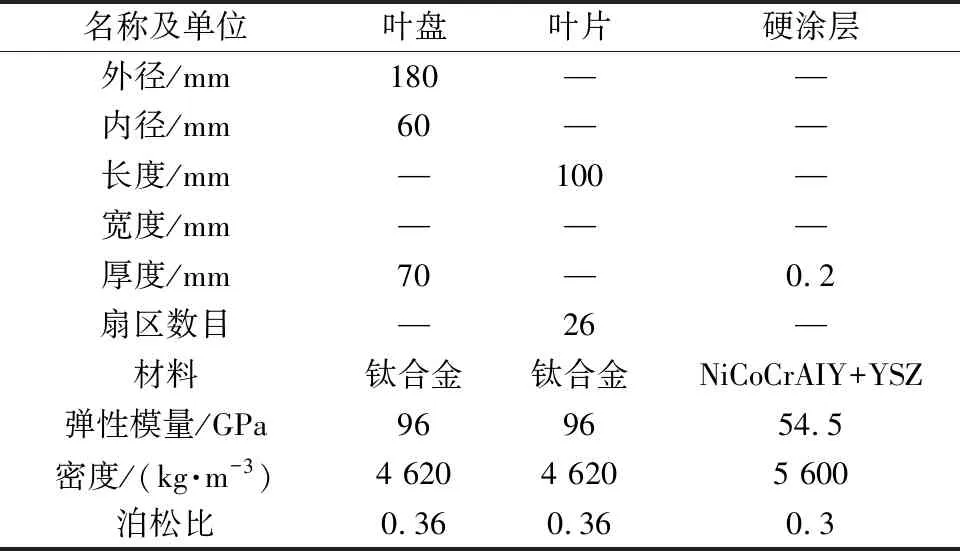
表1 硬涂层整体叶盘的几何参数和材料参数Table 1 Geometric and material parameters of hard-coated monolithic leaf discs

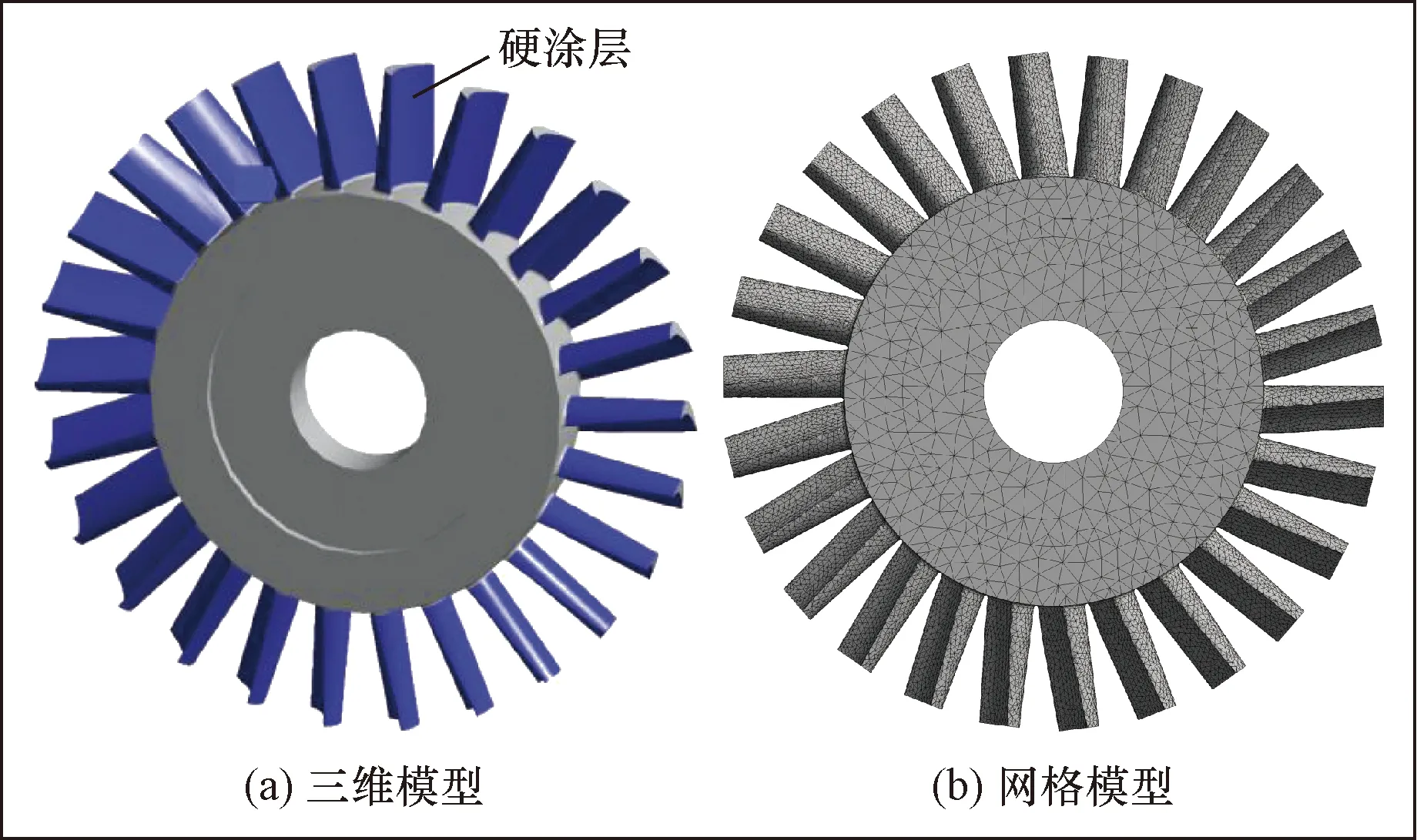
图1 整体叶盘模型Fig.1 Overall leaf disk model

1.2 整体叶盘稳态温度场模型

参考文献[10]可知,涡轮整体叶盘在实际工况下,其叶片部分的温度沿叶径向分布规律大致为叶尖与叶跟温度较低, 叶身中部温度较高。由于冷却作用, 叶盘温度的高低大致服从线性梯度分布。使用一维插值的方法对航空发动机整体叶盘沿径向稳态温度场进行分段插值拟合[11],插值数据如图2所示。

图2 径向温度变化数据Fig.2 Radial temperature variation data

根据图2中的节点参数,设置整体叶盘的温度梯度,获得叶盘的稳态温度场载荷,如图3所示。

图3 整体叶盘的稳态温度场Fig.3 Steady-state temperature field of the overall leaf disc

1.3 整体叶盘流场模型

为了仿真和耦合场计算的方便,建立整体叶盘外流域和内流域场,整体采用四面体单元进行网格划分,并加密流场和整体叶盘接触的面,计算得到915 495个节点和1 294 727个单元。气流方向从左到右,模型边界条件采用压力进口和压力出口,整体叶盘流场的进口压力为160 000 Pa, 出口压力为标准大气压,将它们作为流体分析和固体分析的边界条件。气体冲击受力面为整体叶盘,作为求解量。选择标准的k-ε湍流模型和标准壁面函数,求解时选用SIMPLE算法和二阶迎风格式。流场模型和导入的压力载荷如图4和图5所示。

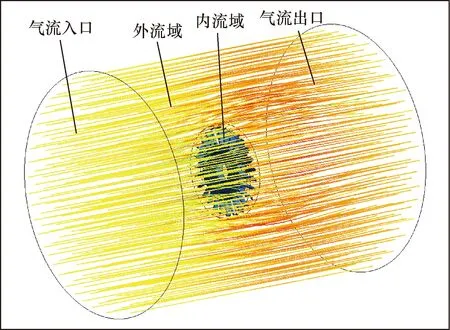
图4 整体叶盘流场模型Fig.4 Integral leaf disc flow field model

图5 压力载荷图Fig.5 Pressure load diagram

2 基本计算理论

对整体叶盘结构进行有限元分析时,首先将结构整体进行离散化处理,再由拉格朗日方程建立其结构的动力学方程[12]为

(1)

系统经过简化后,整体叶盘无阻尼振动方程为

(2)

x=Xsin(ωt+α)

(3)

式中:X为振幅列阵;ω为固有频率;α为初相位。

将式(3)代入式(2)得

(K-ω2M)X=0

(4)

令A=K-ω2M,detA=0,即

(5)

通过求解行列式得出整体叶盘固有频率为

(6)

3 振动特性分析

3.1 固有频率分析

由于整体叶盘具有周期对称性,所以对其结构采用循环对称方式进行有限元分析。分别计算了整体叶盘和硬涂层整体叶盘在3种工况(表2)作用下的前6阶频率。

表2 整体叶盘工况设计Table 2 Overall leaf disc working condition design

考虑到整体叶盘在工作时受到离心和温度载荷影响,计算了整体叶盘在不同转速下的固有频率(表3)。在工况1载荷作用下,随着整体叶盘转速的增加,其中有无硬涂层的整体叶盘一阶和二阶固有频率都逐渐降低,并且在相同转速下涂敷硬涂层使固有频率分别降低2.00%～2.13%、2.04%～2.28%;三阶固有频率不受影响,并且在相同转速下涂敷硬涂层使固有频率降低1.64%;四阶固有频率逐渐下降,并且在相同转速下涂敷硬涂层使固有频率降低1.46%～1.59%;五阶和六阶的固有频率总体趋于升高,并且在相同转速下涂敷硬涂层使固有频率分别降低1.31%～1.34%、1.11%～1.31%。

表3 在工况1下有无硬涂层整体叶盘固有频率对比Table 3 Comparison of intrinsic frequencies of integral leaf disc with and without hard coating at working condition 1

考虑到整体叶盘在工作时受到离心和气动载荷影响,计算了整体叶盘在不同转速下的固有频率(表4)。在工况2载荷作用下,随着整体叶盘转速的增加,其中有无硬涂层的整体叶盘一阶和二阶固有频率都逐渐降低,并且在相同转速下涂敷硬涂层使固有频率分别降低1.99%～2.12%、2.05%～2.30%;三阶固有频率不受影响,并且在相同转速下涂敷硬涂层使固有频率降低1.64%;四阶固有频率逐渐下降,并且在相同转速下涂敷硬涂层使固有频率降低1.45%～1.59%;五阶和六阶的固有频率总体趋于升高,并且在相同转速下涂敷硬涂层使固有频率分别降低1.30%～1.34%、1.10%～1.31%。

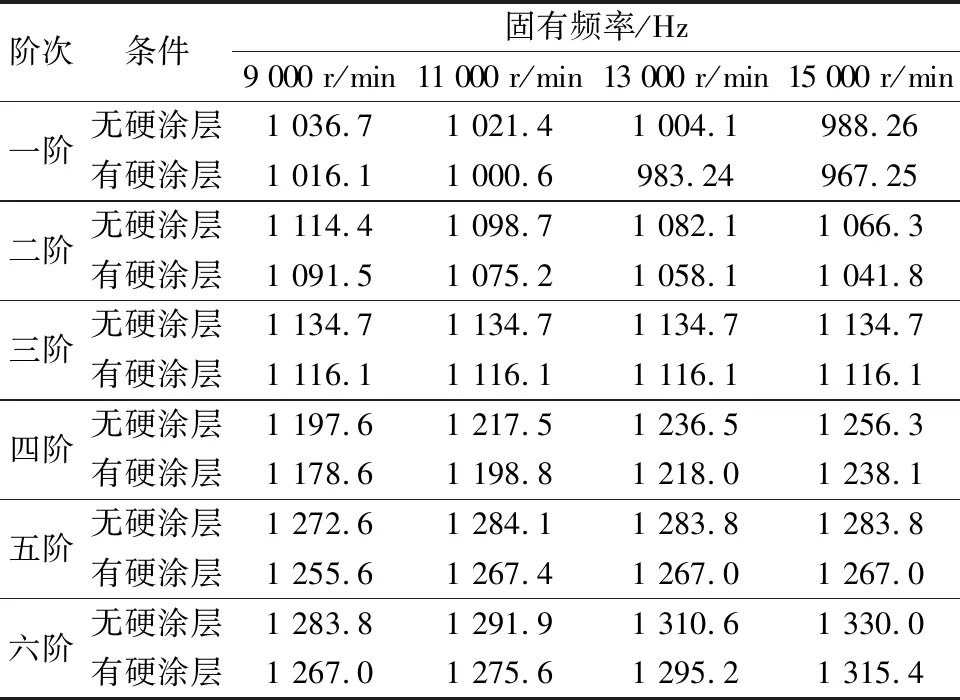
表4 在工况2下有无硬涂层整体叶盘固有频率对比Table 4 Comparison of intrinsic frequencies of integral leaf disc with and without hard coating at working condition 2

考虑到整体叶盘在工作时受到离心、温度和气动载荷影响,计算了整体叶盘在不同转速下的固有频率(表5)。在工况3载荷作用下,随着整体叶盘转速的增加,其中有无硬涂层的整体叶盘一阶和二阶固有频率都逐渐降低,并且在相同转速下涂敷硬涂层使固有频率分别降低1.99%～2.13%、2.06%～2.30%;三阶固有频率不受影响,并且在相同转速下涂敷硬涂层使固有频率降低1.64%;四阶固有频率逐渐下降,并且在相同转速下涂敷硬涂层使固有频率降低1.45%～1.58%;五阶和六阶的固有频率总体趋于升高,并且在相同转速下涂敷硬涂层使固有频率分别降低1.30%～1.35%、1.10%～1.33%。

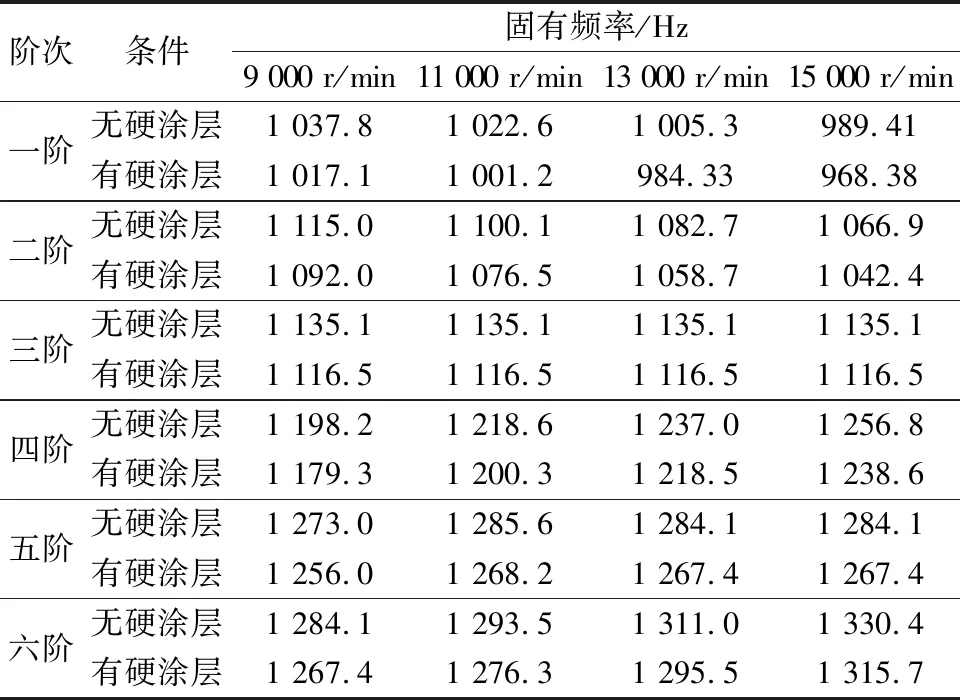
表5 在工况3下有无硬涂层整体叶盘固有频率对比Table 5 Comparison of intrinsic frequencies of integral leaf disc with and without hard coating at working condition 3

比较工况1和工况3可知气动载荷对整体叶盘固有频率的影响,同理比较工况2和工况3可知温度载荷对整体叶盘固有频率的影响。由图6和图7可知,在设定9 000 r/min和15 000 r/min的转速中,在2阶处,气动载荷对有无硬涂层整体叶盘固有频率影响最大,变化率分别为0.74%、0.76%;在1阶处,温度载荷对有无硬涂层整体叶盘固有频率影响的最大变化率均为0.12%。

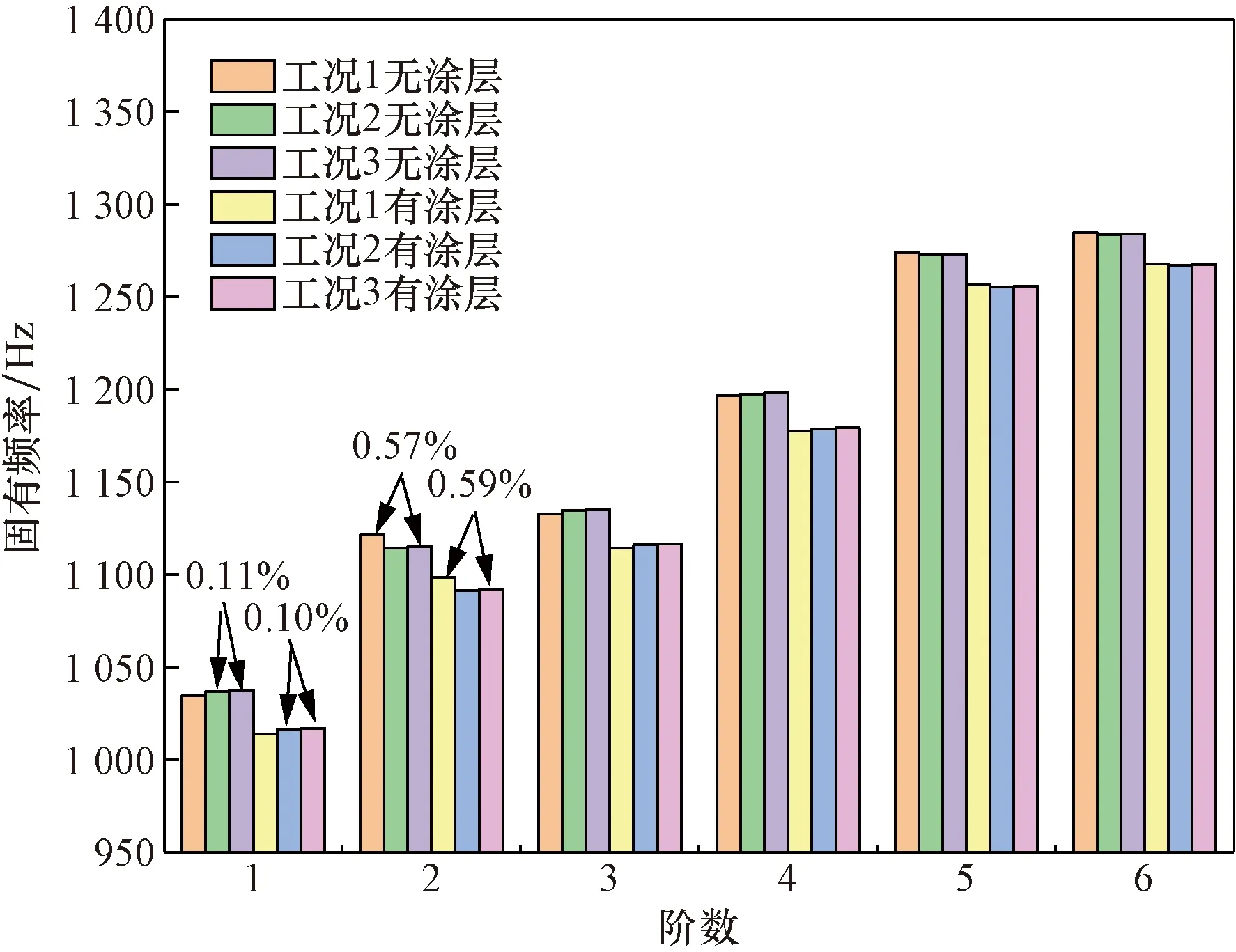
图6 整体叶盘在9 000 r/min下的3种工况固有频率对比图Fig.6 Comparison of the inherent frequencies of the three operating conditions of the integral leaf disc at 9 000 r/min

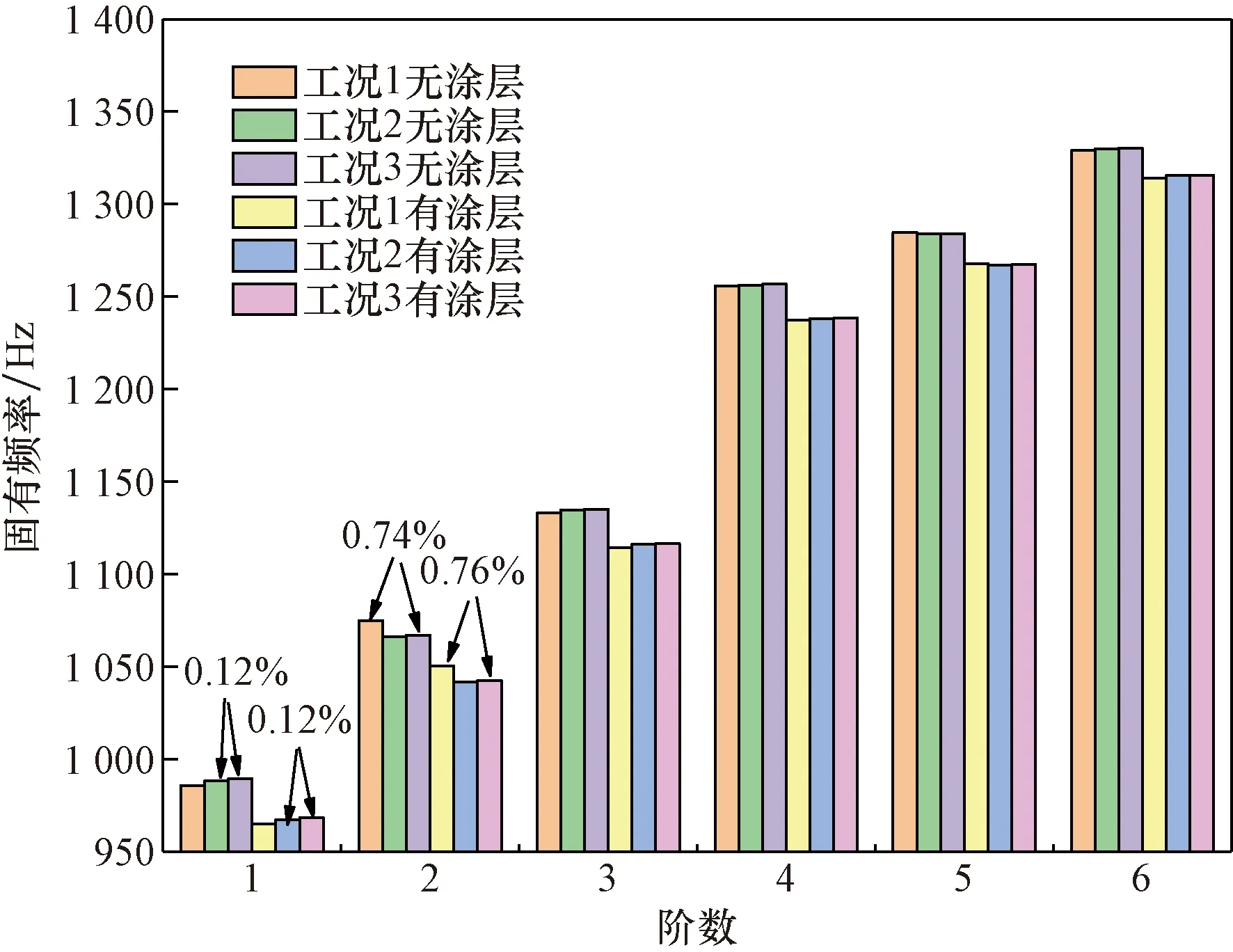
图7 整体叶盘在15 000 r/min下的3种工况固有频率对比图Fig.7 Comparison of the inherent frequencies of the three operating conditions of the integral leaf disc at 15 000 r/min

综合上所述,在3种工况下涂敷硬涂层可以降低航空发动机整体叶盘的固有频率,且影响变化率为1.10%～2.32%;并且对整体叶盘固有频率影响的载荷因素从大到小分别为:气动、温度、载荷。

3.2 振型分析

经过对比可知,有无涂敷硬涂层对整体叶盘振型没有影响。在工况3载荷,转速设置12 000 r/min下对无涂层整体叶盘振型进行分析,得到整体叶盘六阶模态振型图。其中第五阶主要是叶片的弯曲振动,其余阶次主要是叶片和轮盘形成的耦合振动。如图8所示,叶盘的形变量从中心到叶端逐渐增加,叶端达到最大形变,说明整体叶盘叶尖更容易发生变形及振动损伤。

图8 整体叶盘六阶模态振型图Fig.8 Sixth-order mode vibration diagram of integral leaf disc

3.3 谐响应分析

将航空发动机整体叶盘分别在有无硬涂层的条件下进行响应分析,其中谐响应的频率范围设置为0～5 000 Hz内,激振力为1g(g为重力加速度)的激励幅度,位移方向为X方向,提取整体叶盘特征为响应点,其位移响应如图9所示。

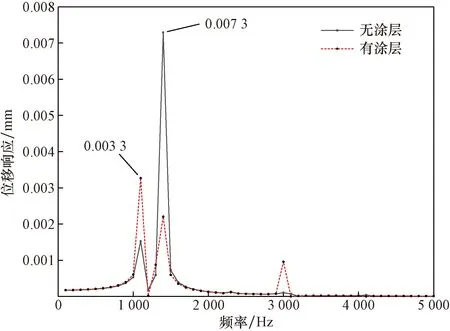
图9 有无硬涂层整体叶盘位移响应对比Fig.9 Comparison of displacement response of integral leaf disc with and without hard coating

由图9可知,在激振频率为1 100 Hz附近时,有硬涂层的整体叶盘振幅响应达到峰值,其位移响应大小为0.003 3 mm;在激振频率为1 400 Hz附近时,无涂层叶盘位移的振幅响应达到峰值,位移响应大小为0.007 3;有硬涂层的整体叶盘比无涂层的响应峰值幅度降低了54.8%;在综合上所述,涂敷硬涂层对叶盘位移响应峰值具有抑制作用。

3.4 共振分析

以整体叶盘模型在工况3载荷条件下进行分析。借助坎贝尔图(Campbell)判断整体叶盘发生共振现象,结果如图10和图11所示。

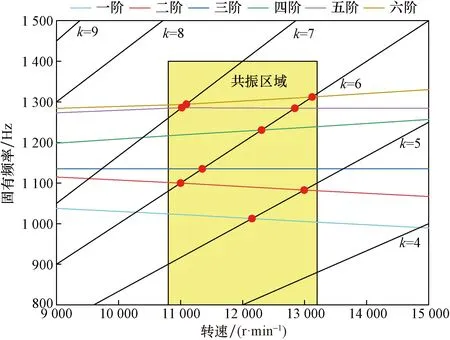
图10 无硬涂层叶盘坎贝尔图Fig.10 Campbell diagram of non-hard coated leaf disc

图11 有硬涂层叶盘坎贝尔图Fig.11 Campbell diagram with hard coated leaf disc

整体叶盘的转速范围设定在9 000 r/min～15 000 r/min,正常工况工作转速设置为12 000 r/min。将整体叶盘每阶固有频率按照9 000、11 000、13 000、15 000 r/min转速下对应的频率值连成线,并计算出发动机在该工作转速时所对应的频率值。严格来说叶盘的共振现象是不可避免的, 但是需要保证叶盘的工作转速尽量远离共振转速区[11]10% (称为共振裕度) 以上, 即可达到避共振要求。其中, 共振裕度η计算公式为

(7)

式(7)中:ντ为共振转速;νω为工作转速。

由图10可以看出,在激振力谐波系数k=5倍激振力的作用下,与第一阶、二阶振动形成共振,其共振转速分别为12 151.7、12 993.1 r/min,裕度分别为1.3%、8.3%;在k=6倍激振力的作用下,与第二阶、三阶、四阶、五阶、六阶振动形成共振,其共振转速分别为11 000.9、11 351.1、12 306.1、12 842.2、13 121.8 r/min,裕度分别为8.3%、5.4%、2.6%、7.0%、9.3%;在k=7倍激振力的作用下,与第五阶、六阶振动形成共振,其共振转速分别为11 019.3、11 094.2 r/min,裕度分别为8.2%、7.5%;而在其他交点处,裕度均大于10%,所以无硬涂层整体叶盘在11 000.9、11 019.3、11 094.2、11 351.1、12 151.7、12 306.1、12 842.2、12 993.1、13 121.8 r/min转速下时较易产生共振。

彩色曲线为一阶～六阶转速和固有频率的关系,射线为k=4～9的激振频率射线,两者的交点为共振点,共振点对应的转速为共振转速[13]

由图11可以看出,在激振力谐波系数k=5倍激振力的作用下,与第一阶、二阶振动形成共振,其共振转速分别为11 921.1、12 732.9 r/min,裕度分别为0.7%、6.1%;在k=6倍激振力的作用下,与第三阶、四阶、五阶、六阶振动形成共振,其共振转速分别为11 165.1、12 103.4、12 675.3、12 950.2 r/min,裕度分别为7.0%、0.9%、5.6%、7.9%;在k=7倍激振力的作用下,与第五阶、六阶振动形成共振,其共振转速为10 863.1、10 937.3 r/min,裕度分别为9.5%、8.9%;而在其他交点处,裕度均大于10%,所以有硬涂层整体叶盘在10 863.1、10 937.3、11 165.1、11 921.1、12 103.4、12 675.3、12 732.9、12 950.2 r/min这些交点转速下,可能发生不同程度的共振。

综上所述,在12 000 r/min工况转速下,以上标记的那些转速均为较危险的工作转速,应在振动分析和结构设计中加以考虑。而且涂敷硬涂层可以使整体叶盘共振点数由9个降为8个。