空间几何解析,坐标建系探究
2023-12-15贺姣妮
数学教学通讯·高中版 2023年10期


[摘 要] 空间几何是高中数学的重点内容,问题解析对学生的空间几何观有一定的要求. 求解时常借助空间向量法,直接利用向量法对应的问题公式转化求解,如角度、距离等问题. 文章对一道高考真题进行解法探究,总结归纳,并结合实例探究向量法建系的四种情形.
[关键词] 空间距离;二面角;坐标系;向量法
真题探究
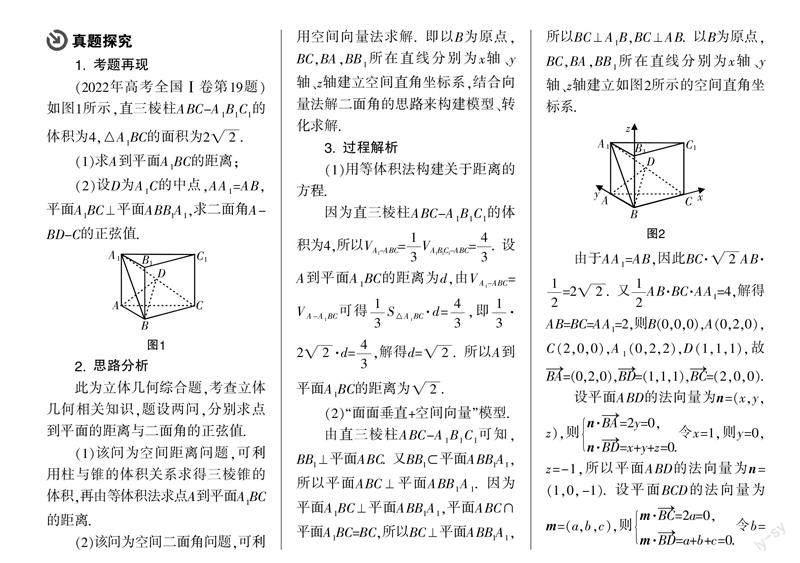
1. 考题再现
(2022年高考全国Ⅰ卷第19题)如图1所示,直三棱柱ABC-ABC的体积为4,△ABC的面积为2.
(1)求A到平面ABC的距离;
教学思考
上述對一道空间向量题开展解题探究,生成利用向量法求解空间角度问题的四种思路. 下面提出两点教学建议.
建议一:挖掘解法的知识背景.
解题探究中除了总结方法外,还要关注知识基础. 如上述用向量法求解空间角度问题,就是基于向量积运算来转化角度问题的. 在探究教学中,可以借助直观模型,引导学生从向量积运算中推导公式,让学生深刻理解公式,灵活运用公式. 同时,开展总结探究,生成模型策略.
建议二:探索解法构建的多种情形.
类型题的破解方法通常有多种构建方式,针对不同情形可选用对应的策略. 以上述向量法建系为例,有四种构建方式,包括棱垂直、线面垂直、面面垂直、底面中心点的高. 在探究教学中,要结合具体问题引导学生思考,体会合理构建坐标系的重要性. 同时指导学生关注空间几何的特殊性质,提取其中的特殊关系,按照“模型提取—特性分析—坐标建系”的思路开展问题探索.
作者简介:贺姣妮(1990—),本科学历,中小学一级教师,从事高中数学教学工作.
