内置分块波纹钢板-混凝土组合剪力墙抗震性能分析

丁习斌 姜艳涛 吴边 张凤亮

摘 要：传统的钢板-混凝土组合剪力墙构造复杂、现场施工难度大，由于连续的钢板将剪力墙的混凝土一分为二，还可能导致墙体整体性变差。为克服上述缺陷，本文提出了一种内置分块波纹钢板的新型钢-混凝土组合剪力墙，并对其抗震性能进行了数值分析。基于ABAQUS有限元计算软件，首先验证了本文提出的建模方法的可靠性，进一步建立了内置水平、竖向分块波纹钢板-混凝土组合剪力墙的非线性数值分析模型。计算结果表明：墙体的滞回曲线饱满，具有良好的延性及耗能能力；波纹钢板的放置方向对墙体性能的影响很小； 加大轴压比或减小高宽比都会降低墙体的延性。

关键词：分块波纹钢板；钢-混凝土组合剪力墙；有限元分析；数值模拟；抗震性能

中图分类号：TU317

文献标志码：A

近年来大量超高层剪力墙结构、框架-核心筒结构的出现，对剪力墙构件的设计提出了更高的要求。相较于传统的钢筋混凝土剪力墙，钢板-混凝土组合剪力墙能显著提高剪力墙的抗震性能，减少截面面积，在复杂高层、超高层结构中有着广泛应用。

由于钢板-混凝土组合剪力墙与钢筋混凝土剪力墙在抗震性能、受力-变形机理、设计方法等多方面存在差异，有必要开展系统的研究。早年间日本学者对开缝钢板组合剪力墙进行了研究，墙两侧利用混凝土盖板对整块钢板进行限制，防止钢板发生整体或者局部屈曲［1］。尽管试验证明了该墙的性能较为良好，但混凝土只对钢板起限制作用，并未完全发挥性能。孙建超等［2］也对钢板组合剪力墙进行了大量研究，共设计了11个剪跨比为1.5的钢板组合剪力墙，试验结果表明该种形式的墙体中，混凝土与钢板能够很好地发挥作用，两种材料的优势均得到充分利用，提高了组合剪力墙的抗剪承载力以及延性等力学性能。试验还研究了钢板的连接形式，提出了钢混组合剪力墙的抗剪截面控制公式。相较于平钢板，波纹钢板具有面外刚度更大，与混凝土有更好的结合受力等优点。SHAHMOHAMMADI等［3］研究了不同形式的波纹钢板-混凝土组合剪力墙，并与平钢板组合剪力墙性能进行对比，验证了波纹钢板剪力墙性能的优越性。张良等［4］提出了“承重抗侧分离”的波形钢板-钢管混凝土柱组合剪力墙，采用数值分析等方法研究了其抗震性能。郝婷玥［5-6］等对钢板-混凝土组合剪力墙进行了轴压试验，着重研究了钢板与混凝土不同连接形式对试件整体承载力以及耗能能力等性能的影响。试验结果表明栓钉连接能够保证钢板和混凝土的良好结合，墙体整体性能良好。曹万林等［7］对内置分块平钢板的双肢剪力墙进行了研究，主要对4个1 ∶5的缩尺模型进行往复加载，结果表明该种墙体抗侧刚度大，耗能能力良好，抗震性能优秀。

针对施工过程中钢板易变形及模板固定困难等问题，汪潇驹等［8］采用了样板墙试验确定混凝土配合比，利用BIM技术降低钢筋绑扎难度，保证了组合剪力墙浇筑质量。为满足组合钢板墙模板施工的需要，在钢板剪力墙上间隔布置对拉螺杆套筒及开设对拉螺杆孔［9］。董传艺等［10］通过减少钢板剪力墙的焊接作业量来控制钢板的变形。

尽管国内外学者对于钢板-混凝土组合剪力墙已经有了较深入和系统的研究，但主要还是围绕墙体内置整块钢板的这一类构造方式，对于采用分块钢板的构造形式的研究还比较少。本文在已有研究基础上，通过建立三维有限元数值分析模型，详细分析了内置分块波纹钢板-混凝土组合剪力墙的抗震性能，对后续开展试验研究以及参数分析提供参考。

1 数值模型建立

1.1 建模方法

利用ABAQUS有限元软件建立模型，混凝土采用C3D8R实体单元，型钢柱及钢板采用壳单元，钢筋采用2节点的T3D2桁架单元。因网格划分对于模型收敛以及结果的准确性有较大影响，所以对模型的网格精细划分为标准的六面体单元，尺寸取50 mm。模型边界条件尽量符合实际受力过程中的约束条件，底部完全固定，将剪力墙顶面自由度耦合于一点，用于轴力以及水平位移荷载的施加。钢板及型钢与混凝土采用面面接触，法向为硬接触，切向采用罚函数定义摩擦，摩擦系数取0.3，考虑钢筋与混凝土之间的滑移。

1.2 材料本构模型

1.2.1 剪力墙混凝土本构模型

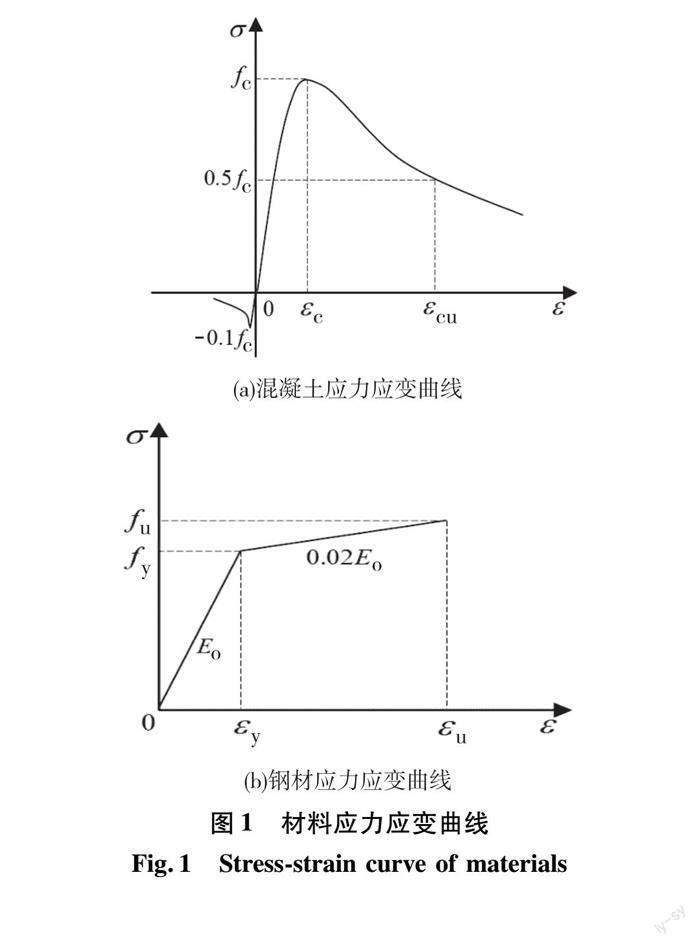
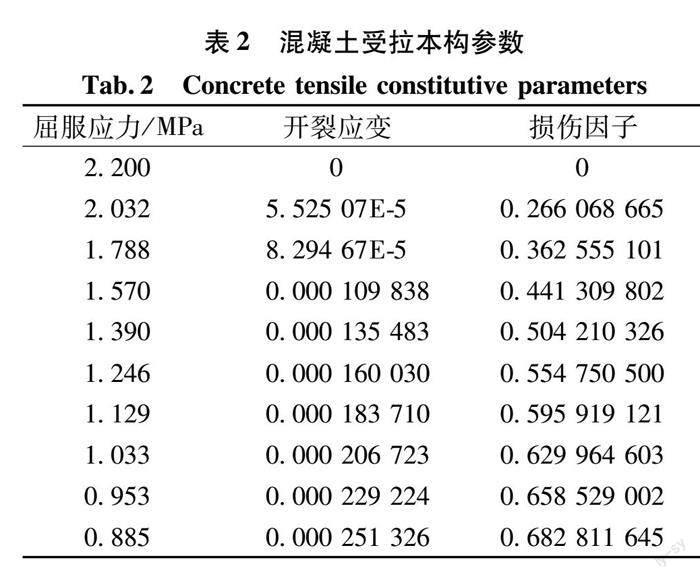
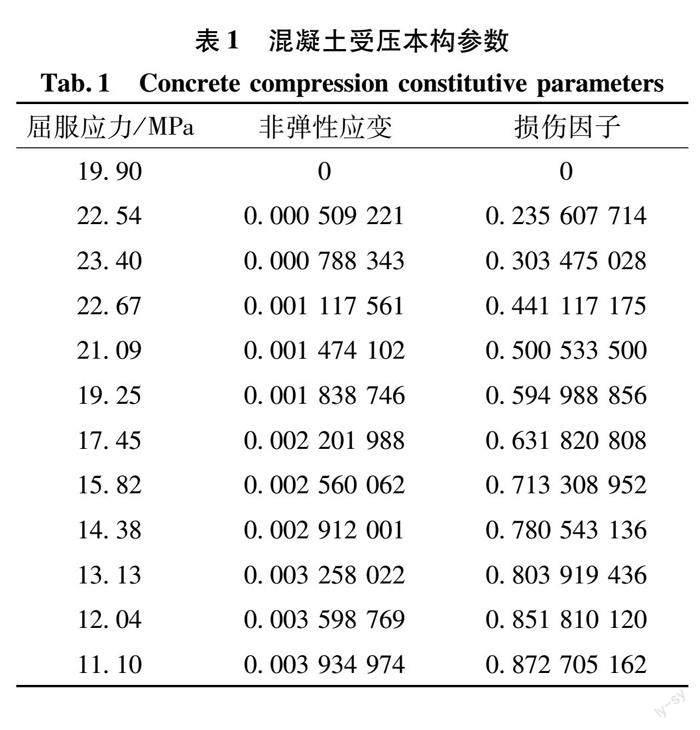
采用ABAQUS软件提供的混凝土损伤塑性模型，该模型考虑了混凝土在承受荷载过程中的受拉或者受压破坏，混凝土的应力-应变曲线（图1（a））的计算则参考《混凝土结构设计规范》（GB50010—2010），具體参数如表1、表2所示。

1.2.2 钢材本构模型

钢材本构（图1（b））为双折线模型，该模型在钢材屈服前保持线性，斜率为初始弹性模量，在钢材屈服进入塑性阶段之后应力应变依然保持线性关系，塑性阶段折线斜率取初始斜率0.02倍。

2 模型建立及验证

2.1 模型建立

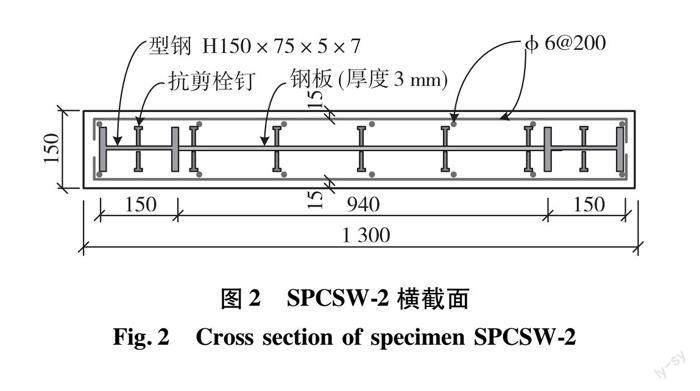
为验证ABAQUS有限元建模及数值分析方法的正确性，对文献［11］中SPCSW-2试验构件（图2）进行数值模拟。该试验剪力墙试件的尺寸为1 300 mm×150 mm×1 978 mm，采用HRB335级钢筋，钢筋间距200 mm，钢板采用Q235型钢材，厚度为3 mm，混凝土强度等级为C40，型钢尺寸为H150 mm×75 mm×5 mm×7 mm，墙体轴压比0.2，加载方式采用往复位移加载。有限元模型如图3所示。

2.2 结果验证

图4为有限元计算结果与文献［11］试验结果骨架曲线的对比图，二者拟合基本良好，在弹性阶段两条曲线基本一致；结构发生屈服后，有限元分析结果相较于试验结果荷载略大，原因可能是建模过程中没有考虑钢筋与混凝土的滑移，同时实际试验的结构可能存在一些缺陷，而在有限元分析中没有考虑；如图4所示，当试验结构承载力下降临近破坏时，有限元结果并没有很明显的下降，可能是因为有限元中钢材本构采用双折线模型，承载力下降不够明显。但综合来看，有限元结果与试验结果基本相符，误差较小，验证了数值模拟的可靠性。

3 分块波纹钢板-混凝土组合剪力墙性能分析

3.1 分块波纹钢板-混凝土组合剪力墙

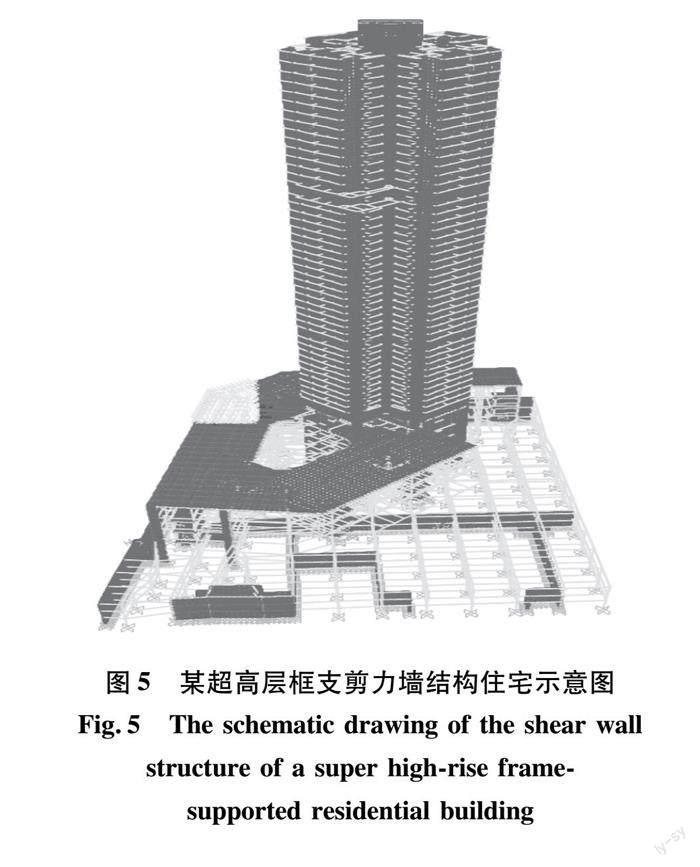
分块波纹钢板-混凝土组合剪力墙的提出源于深圳市某超高层住宅项目。该住宅项目包含了多栋高度超过150 m的框支剪力墙结构建筑（图5），由于结构高度高且受到建筑使用功能的限制，出于降低墙厚的考虑，在结构的底部加强部位采用了钢板-混凝土组合剪力墙。钢板-混凝土组合剪力墙虽然有效减小了底部剪力墙的厚度，然而大片连续钢板的使用，给结构的施工带来的较大的困难。此外，由于整块钢板将混凝土一分为二，混凝土与钢板间容易出现分离，导致墙体的整体性变差，降低其抗震性能。

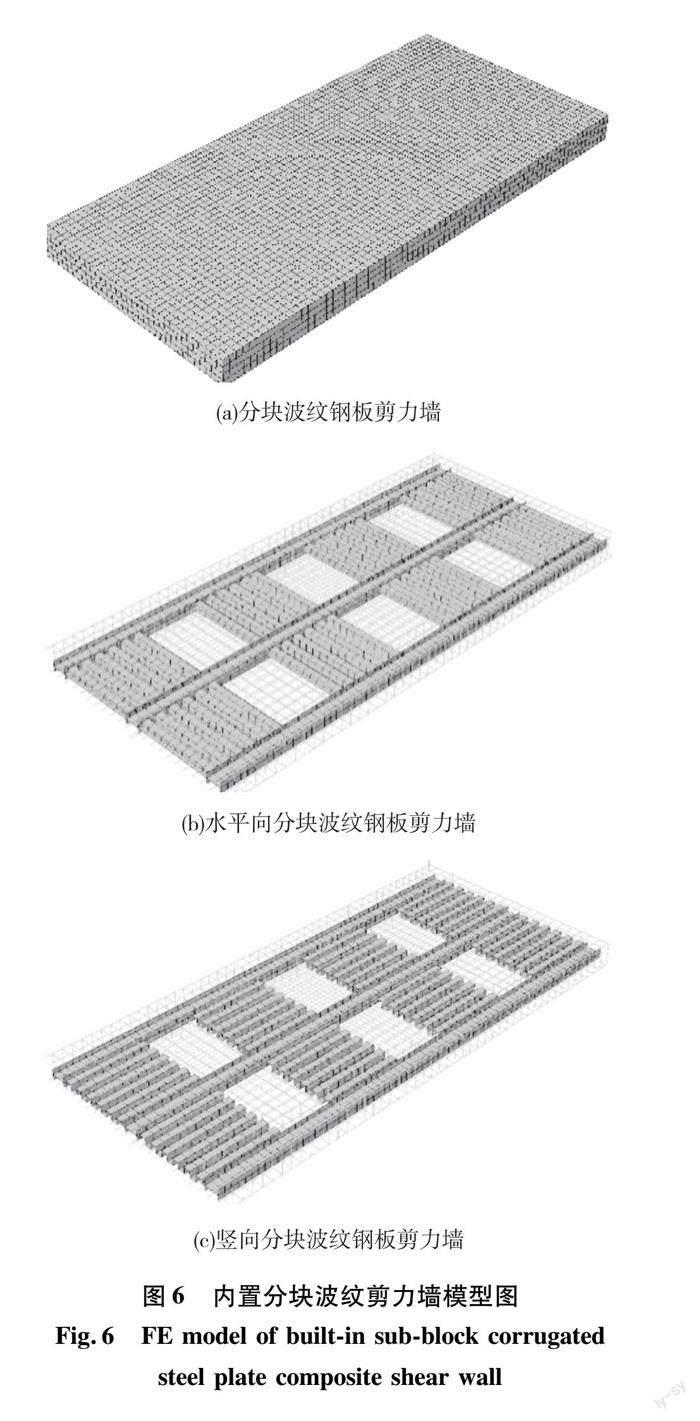
为了解决传统的钢板-混凝土组合剪力墙的上述缺陷，本文提出了分块波纹钢板-混凝土组合剪力墙的设计。如图6所示，该设计采用了型钢骨架约束的分块波纹钢板替代整块钢板，将其内置于混凝土剪力墙中。相较于传统的钢板-混凝土组合剪力墙，该设计有3个主要优点：（1）采用分块钢板为剪力墙模板的对拉螺杆留出了大量空间，组合剪力墙的施工过程中，无需进行钢板开孔、对位等工序，提高了施工效率;（2）采用分块钢板有利于钢板两侧的混凝土形成整体，组合剪力墙不会出现混凝土与钢板间的分离现象，有利于增强钢板、混凝土的组合效应;（3）分块钢板采用波纹钢板而非平钢板，这种构造方式可有效提高钢板的平面外刚度，防止其出现局部屈曲，同时还增强了钢板与混凝土间的黏结作用，减少了抗剪栓钉的使用。

3.2 组合剪力墙试件设计

为了验证分块波纹钢板-混凝土组合剪力墙的抗震性能，分别设计了钢板波纹方向不同的两种形式的组合剪力墙试件（CSW1和CSW2）。试件的尺寸为3 400 mm×400 mm×7 200 mm，均采用HRB400级钢筋，纵筋直径25 mm，箍筋及水平筋均为14 mm，内置钢板厚13 mm，波角为90°，CSW-1含钢量3.43%，CSW-2含钢量为3.37%，钢材均采用Q345型，型钢为H250 mm×150 mm×13 mm×13 mm，本次模拟混凝土等级选为C35，墙体轴压比为0.2，剪跨比为2.1，剪力墙截面如图7所示。采用第2节所述建模方法，分别建立了上述剪力墙试件的有限元模型（如图6所示）。

考虑到有限元模拟不存在仪器测量误差，采用拟静力试验中常用的力-位移混合式加载制度反而会增加模拟的复杂程度。因此，按照位移控制方式进行加载，对于力加载阶段，由于该阶段试件基本处于弹性，假定按线性关系将力换算为位移。

3.3 内置分块波纹剪力墙性能分析

3.3.1 应力云图

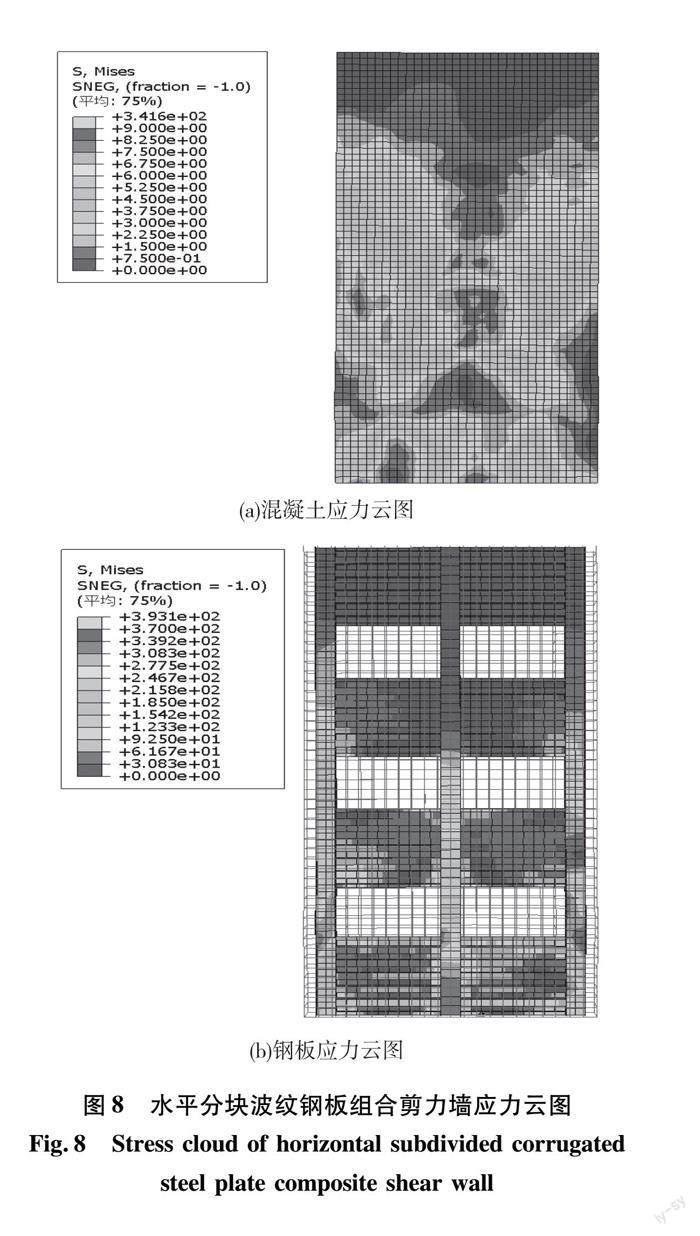
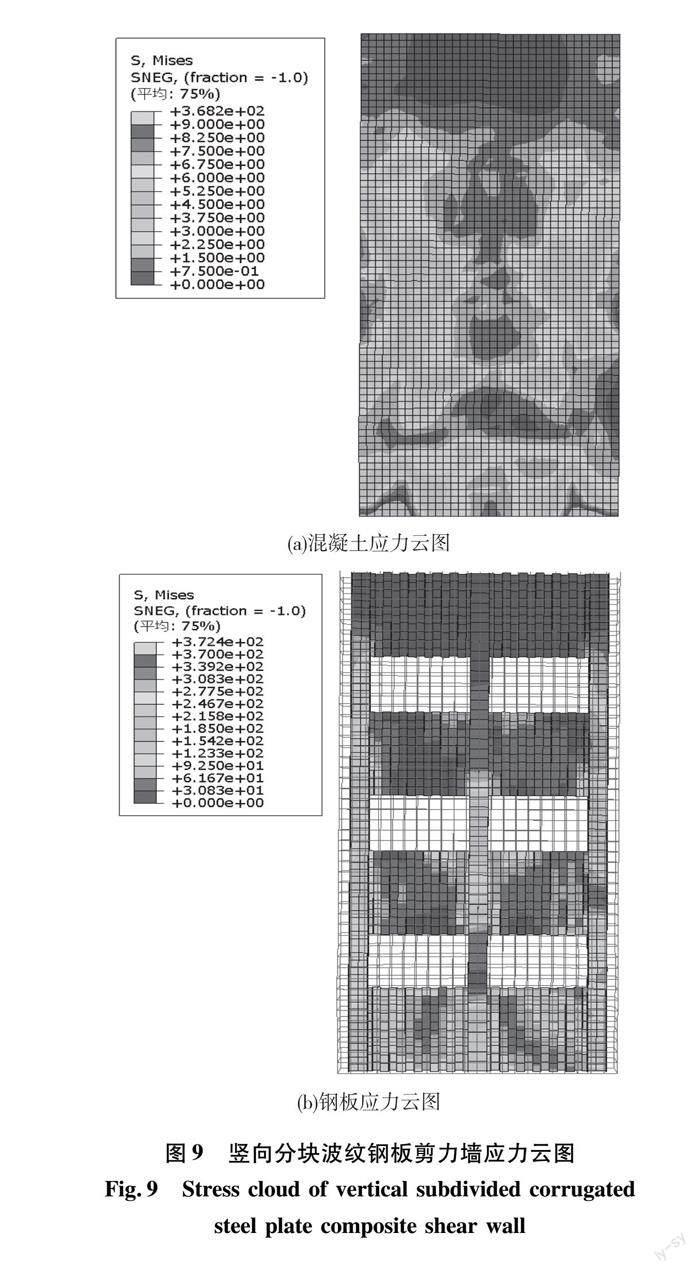
两种形式剪力墙的应力云图分别如图8、图9所示，由于本文研究的钢板剪力墙是将传统剪力墙的整块钢板切割成小块波纹钢板，所以分块钢板间成为了墙体的薄弱部位。从混凝土应力发展来看，两片剪力墙均从墙体的中下部边缘开始出现破坏，随着荷载的施加逐步向墙体中部发展；从钢板应力发展来看，主要从底部第一个钢板分界处开始出现破坏。在荷载作用下，墙体中混凝土及钢板均表现为顶部应力较小，破坏主要集中体现在中下部的薄弱部位。应力云图反应了两种形式的剪力墙在承受相同荷载的情况下，性能相差不大，需要进一步对该种形式墙体进行研究分析。

3.3.2 滞回曲线及骨架曲线

滞回曲线又称恢复力特性曲线，是结构或者构件在往复荷载作用下结构恢复力随着变形变化的曲线，多通过对结构或构件的拟静力试验来确定，是对结构进行抗震分析的基础。骨架曲线则是将往复荷载作用下所得到的滞回曲线的拉或压各级加载的极值荷载前后相连所得到的曲线。该曲线模型能够很好的反应结构或构件在承受荷载的情况下不同阶段的结构特性。

通过对两个模型的计算，得到如图10滞回曲线与图11骨架曲线。两种构造的剪力墙在往复荷载作用下的滞回曲线饱满程度相差很小。采用冯鹏等［12］提出的最远点法计算各试件的屈服点，得出水平分块波纹钢板剪力墙屈服位移为12 mm，竖向分块波纹钢板剪力墙屈服位移为13.9 mm，对应的屈服荷载分别为1 905.3 kN、1 802.4 kN。原因是当剪力墙承受水平荷载时，由于水平分块波纹钢板无法或者发生很小的面内变形，侧向刚度比较大，而竖向分块波纹钢板由于所承受的侧向荷载和波纹方向垂直，导致波纹钢板在受力时可以发生类似于手风琴式的变形（即顺波纹方向拉伸和压缩会使其刚度降低），延性较好。骨架曲线反应出在弹性阶段两种墙体的曲线完全重合，进入塑性阶段则出现了一些不同，水平分块波纹钢板刚度依旧较大。塑性阶段的曲线发展表明两种墻体出现很小的下降段后就趋于平缓，并没有出现实际试验中下降到85%的现象，原因是模拟过程中钢材本构并没有设置下降段，当混凝土发生破坏，结构承载力开始下降，混凝土退出工作后，则主要由型钢柱及钢板组成的钢框架承担主要荷载。

通过对滞回曲线及骨架曲线的分析，发现两种不同放置方式的波纹钢板剪力墙抗震性能相差不大，滞回曲线呈现出较为饱满的梭形，表明该类型剪力墙的塑性变形能力很强，具有很好的耗能能力和抗震性能。

3.3.3 刚度退化曲线

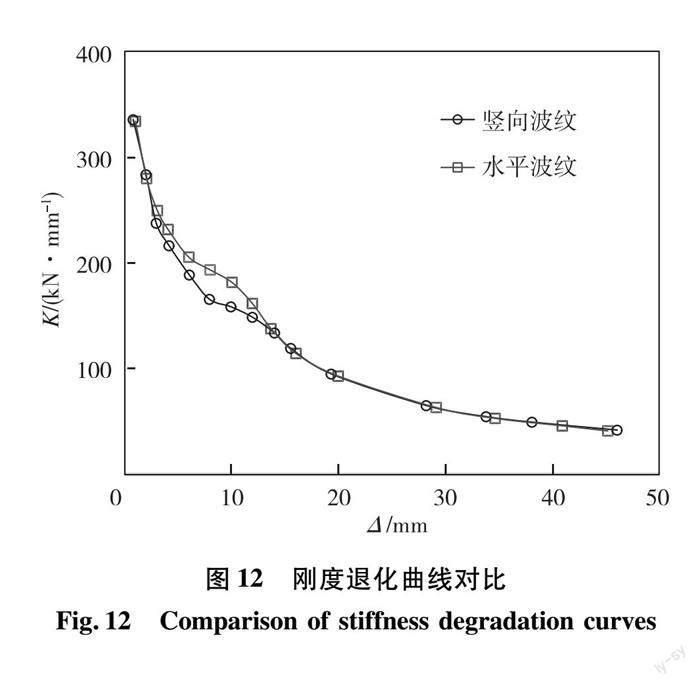
当结构承受往复荷载作用并且想要保持相同的峰值荷载时，相应的位移会随着往复荷载的次数增加而增加。墙体出现变形或裂缝等，都会导致结构的刚度退化。

图12表明随着波形钢板的屈服，结构的刚度下降幅度较大，由于水平钢板在承受侧向力时不会产生“手风琴效应”，所以在这一阶段两种剪力墙的刚度又有所不同。随着水平荷载的逐渐增大，钢板屈曲后对水平荷载的承受占比逐渐减小，结构刚度逐步下降并趋于平缓。

3.4 轴压比对结构性能的影响

为探究轴压比对组合剪力墙抗震性能影响，本文分析了轴压比分别为0.2、0.3、0.4、0.5时组合剪力墙的荷载-位移曲线，墙体其他参数保持不变。图13表明随着轴压比的提高，结构的初始刚度逐渐增大，当轴压比为0.5时，屈服位移明显小于其他三种情况，结构承载力退化速度加快。轴压比由0.2增大到0.4时，屈服位移略有增大，但不明显，当结构处于退化阶段时，结构刚度退化较快，综合来看，当结构轴压比为0.3时，结构能够充分发挥作用，抗震性能良好。

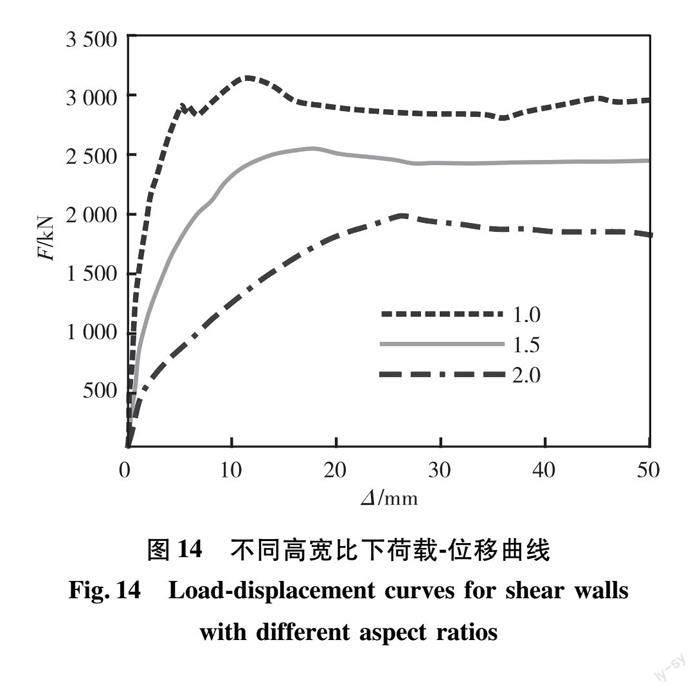
3.5 高寬比对结构性能的影响

对轴压比为0.2，三种不同高宽比的组合剪力墙（分别为1.0，1.5，2.0）进行的数值模拟结果如图14所示。随着组合剪力墙高宽比的减小，即随着组合剪力墙由弯曲变形为主的高墙转变为由剪切变形为主的低矮墙时，剪力墙的承载力、刚度逐步提高。本例中，高宽比由2.0减少到1.0后，剪力墙的承载力提高了约50%。但是，墙体的屈服位移也随之显著减小，导致其整体的延性变差。

4 结论

本文对水平向和竖向的分块波纹钢板-混凝土组合剪力墙进行了分析。首先对建模及数值分析方法的正确性进行了验证，计算与试验结果的骨架曲线拟合良好，表明模拟结果可靠；随后对水平以及竖向的分块波纹钢板剪力墙相关参数进行分析，结果表明：

1）水平向以及竖向的分块波纹钢板-混凝土组合剪力墙的滞回曲线以及骨架曲线相似，结构性能差别不大；

2）分块波纹钢板-混凝土组合剪力墙滞回曲线饱满，具有良好的延性及耗能能力，结构的抗震性能良好；

3）当轴压比不超过0.4时，分块波纹钢板-混凝土组合剪力墙的力学性能良好，钢板和混凝土的材料性能都能得到充分的发挥；

4）随着高宽比的减小，分块波纹钢板-混凝土组合剪力墙的承载力逐步提高，但是其屈服位移减小、延性变差。

本文初步分析了分块波纹钢板-混凝土组合剪力墙的抗震性能。相较于传统的钢板-混凝土组合剪力墙，分块波纹钢板-混凝土组合剪力墙易于施工，墙体具有整体性好、构造简单等优点。同时，分块波纹钢板-混凝土组合剪力墙还具备良好的抗震性能，可替代传统的钢板-混凝土组合剪力墙，用于高层、超高层剪力墙结构底部加强区。

参考文献：

ASTANEH-ASL A. Seismic behavior and design of composite steel plate shear walls［R］. California： Structural Steel Educational Council，2002.

［2］ 孙建超， 王杨， 孙慧中，等. 钢板混凝土组合剪力墙在中国国家博物馆工程中的应用［J］. 建筑结构， 2011， 41（6）： 14-19.

［3］ SHAHMOHAMMADI A， MIRGHADERI R， HAJSADEGHI M， etc. Application of corrugated plates as the web of steel coupling beams［J］. Journal of Constructional Steel Research， 2013， 85（5）： 178-190.

［4］ 张良， 吴边， 张凤亮，等. 波形钢板加强的钢管混凝土组合剪力墙抗震性能分析［J］.工业建筑， 2022， 52（10）： 146-155， 138.

［5］ 郝婷玥， 曹万林， 董宏英，等. 不同构造内置钢板-混凝土组合剪力墙轴压性能试验研究［J］. 建筑结构学报， 2016， 37（5）： 20-28.

［6］ 郝婷玥， 曹万林. 双钢板混凝土组合剪力墙轴压承载力研究［J］. 工程科学学报， 2017， 39（11）： 1765-1773.

［7］ 曹万林， 刘皞， 董宏英，等. 内藏不同高宽比分块钢板双肢剪力墙抗震性能试验研究［J］. 地震工程与工程振动， 2016， 36（5）： 1-9.

［8］ 汪潇驹， 马骏， 张雪斌，等. 钢板混凝土组合剪力墙施工技术［J］. 建筑技术， 2018， 49（7）： 737-740.

［9］ 王铁梦. 工程结构裂缝控制“抗与放”的设计原则及其在“跳仓法”施工中的应用［M］. 北京： 中国建筑工业出版社， 2007.

［10］董传艺， 郭强， 王帅，等. 超高层建筑项目中的核心筒组合钢板剪力墙施工技术［J］. 建筑施工， 2021， 43（1）： 37-39.

［11］高敬宇. 波形钢板剪力墙及组合墙抗震性能试验研究［D］. 西安： 西安建筑科技大学， 2017.

［12］冯鹏， 强翰霖， 叶列平. 材料、构件、结构的“屈服点”定义与讨论［J］. 工程力学， 2017， 34（3）： 36-46.

（责任编辑：于慧梅）

Seismic Performance Analysis of Segmented Corrugated Steel

Plate-Concrete Composite Shear Walls

DING Xibin1， JIANG Yantao2， WU Bian*2， ZHANG Fengliang2

（1.Construction Engineering Company of China Railway No.5 Engineering Group Co.， Ltd.， Guiyang 550081， China;

2.School of Civil and Environmental Engineering， Harbin Institute of Technology （Shenzhen）， Shenzhen 518055， China）

Abstract：

The traditional steel-concrete composite shear wall is complicated in configuration and is difficult to construct on site， and the shear wall integrity may deteriorate due to the continuous steel plate bisecting the concrete of the wall. In order to overcome those shortcomings， an innovative design of steel-concrete composite shear wall with built-in segmented corrugated steel plate is proposed in this paper， and its seismic performance is investigated numerically. Firstly， based on the ABAQUS software， the simulation approach used herein was firstly verified. Then， nonlinear numerical analysis models for the composite shear wall with the horizontally and vertically placed corrugated steel plates were further established. The results show that： the hysteresis curve of the shear wall is full， with good ductility and energy dissipation capacity; the placement direction of the corrugated steel plate has little effect on the performance of the wall; increasing the axial compression ratio or decreasing the shear-span ratio would weaken the ductility of the wall.

Key words：

segmented corrugated steel sheets; steel-concrete composite shear wall; finite element analysis; numerical simulation; seismic performance