厚松散层下开采覆岩及地表移动变形规律试验研究

夏筱红, 魏宏涛,2, 杨伟峰, 徐洪远, 张方正

(1.中国矿业大学资源与地球科学学院, 徐州 221116; 2.中交第一航务工程勘察设计院有限公司, 天津 300222)

煤炭开采后将引起围岩破碎垮落,变形失稳而产生位移、开裂,直至上覆岩土层整体移动变形、弯曲下沉,采动过程将在空间上形成性质复杂的采空区,而在地表形成移动下沉盆地。中外专家从不同的研究角度,依据不同的标准,进行了采掘引起的地面沉降影响范围及采空区上覆岩层移动变形规律的研究[1-4],学者们对采动覆岩与地表移动变形特征的研究主要集中于理论分析与计算、相似材料模型实验、数值模拟和监测等方面,方法较多,成果较为丰富[5-7]。通过干涉式合成孔径雷达(interferometric synthetic aperture radar,InSAR)时序处理Sentinel-1A影像技术,王智纯等[8]开展了新疆西准噶尔沙吉海地区采空区地表形变时空特征研究。李学良[9]采用光纤-微震相结合的方法,对煤矿老采空区覆岩移动变形进行了监测研究,该实时监测能够满足预期监测目的。王晓蕾[10]等论述与分析了煤层开采地表沉陷监测及预测过程与技术方法。

对地表移动变形特征与松散层厚度的关系也开展了很多研究[11-13]。厚松散层下采煤地表移动规律有其独特性,基岩和松散层存在一定的耦合关系。基岩的厚薄、能否形成对上覆土层的结构控制,都将影响着上覆岩土体结合程度和地表的移动变形特征[14]。许延春等[15]提出当松散层很厚时应按土层埋深和沉积年代分段划分松散层移动角量。彭林军等[16]通过对深部开采沉陷结构力学模型的研究,提出了盆地水平煤层地表沉陷的理论预测模型。彭世龙等[17]针对厚松散层薄基岩煤层开采建立了采动与底含疏降水共同作用下地表沉陷预计模型,探讨了此条件开采地表沉陷特征及其主要影响因素。王永辉等[18]针对某煤矿巨厚松散层下开采沉陷问题,探索了地表变形规律和地下岩土体移动特征。上述成果丰富了矿山开采岩移理论,但对于特定条件的沉降变形区仍需开展有针对性的研究。

针对厚松散层下煤层开采覆岩及地表移动变形问题,以山东兖州矿区某煤矿的地质条件为研究背景,采用相似材料模型试验,研究采动过程中覆岩破坏规律,监测地表及各层覆岩移动变形指标的变化,探索采掘结束后的地表持续变形特征。研究成果不仅对矿区工程建设用地及线路规划选址提供技术依据,而且丰富了厚松散层这种特殊地质条件下开采地表移动变形规律的理论研究。

1 研究区地质条件

兖州矿区某煤矿,该区面积约2.2 km2,研究区煤系整体构造形态为一倾向东的单斜构造,地层有起伏形成宽缓的褶曲;井田内的大、中型断层多以正断层形式产出,且具有多期活动特征。该煤矿二叠系下统山西组,属于一套过渡相、陆相碎屑岩含煤沉积建造,主采3煤层厚度为7.9～9.2 m,平均8.5 m,倾角0°～15°,平均8°,为近水平煤层。煤系地层上覆第四系厚度182.2～196.2 m,属于厚松散层,3层煤上覆基岩厚30～80 m。3煤区北部较为普遍的分布有厚薄不等的底黏土层,钻孔揭露厚度3.24～6.80 m,南部则局部分布,底黏土的赋存起到了阻隔第四系松散层底部含水层与基岩风化带的水力联系作用。基岩风化带岩性以细砂岩为主,发育垂直小裂隙,但多为泥质充填,为弱含水层或微弱含水层基本干燥无水,开采过程中覆岩及地表移动变形时可忽略含水层突水造成的影响。

研究区煤矿3煤上覆岩层及土层可按其成因类型、岩性岩相、成层条件与厚度变化、结构特征以及物理力学特征等组合,进行工程地质岩(土)层(组)的划分,由此概化地质原型,构建地质模型,为模型试验的材料配比与铺设奠定基础。

2 相似材料模型设计

2.1 模型设计

本试验以研究区煤矿9301工作面作为原型,位于矿区北部,所采煤层为二叠系山西组3煤,工作面煤层采厚2.2 m,工作面走向约1 600 m,斜长200 m。依据相似理论及模型架尺寸,取几何相似比Cl=200,时间相似比Ct=14.14,根据原型与模型的应力比值,确定应力相似比Cσ=334,根据前三者可得到密度相似比Cγ=1.67。

试验所采用的模型架400 cm(长)×30 cm(宽)×200 cm(高),根据模型设计尺寸调节其高度。模型设计采厚为1.1 cm,模型两侧各留设相应煤岩柱,底板铺设厚度为20 cm,模型总高137.25 cm。

2.2 相似材料选择

模型试验的组成主要包括骨料和胶结物,本次试验以河砂作为主要材料,即骨料;石膏,碳酸钙作为胶结物;除此之外,考虑到煤层埋深较大,且上覆岩土层包含厚松散层,故以质量较轻的锯末作为配料,用以模拟松散地层;另外,用云母粉及云母片起到分层的作用。依据矿区岩土样物理力学指标(表1),按前述相似比制作不同岩土层材料配比试样,并进行力学测试校核。

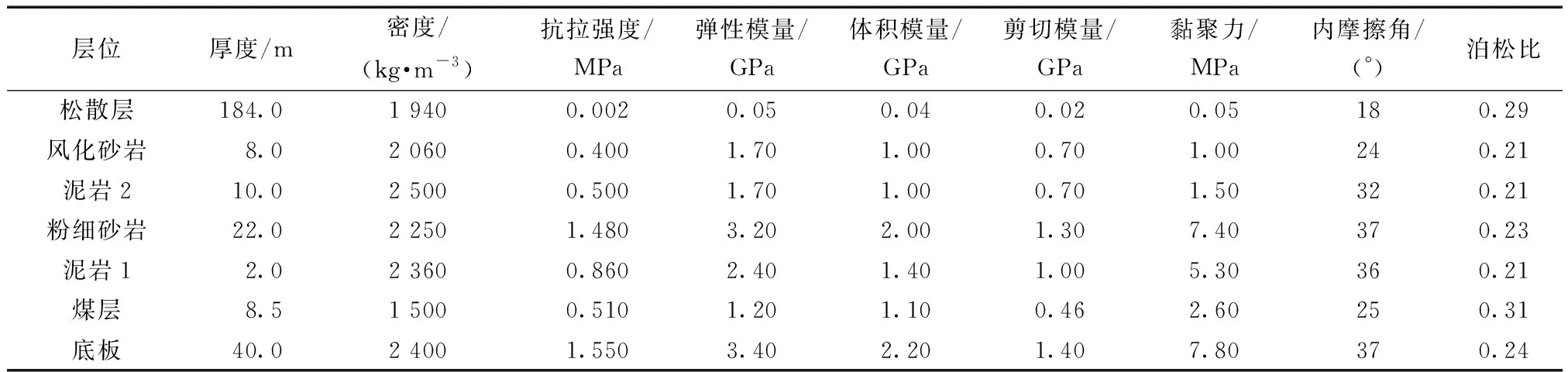
表1 岩土样物理力学参数

2.3 监测设计

采用百分表及布设监测线的方式,共布设4层百分表,分别在地表以及距地表30、60、90 cm处,每层布设7个,共计28个百分表,等间距布设(图1);另外,在模型表面布设位移监测点,采用固定机位拍摄法,对开采过程中的位移进行实时监测记录,再通过计算机软件对各测点进行后处理。

图1 模型位移测点布设图Fig.1 Layout of model displacement measuring points

3 试验结果分析

3.1 覆岩破坏高度及变化情况

模拟开采时,对预先设置的煤层从左至右依次开挖,两侧留足尺边界煤柱,每次开采5 cm,共开采40次,开采时间间隔3 h,开采总时间120 h。开采过程中覆岩变形破坏特征如图2所示。

监测开挖至模型稳定覆岩变形破坏情况,可分4个阶段,具体如下。

(1)初次垮落阶段。当煤层开采35 cm(相当于实际开采70 m)时,模型直接顶板泥岩出现初次垮落。在此之前,由于工作面推进距离较短,未达到岩体破裂所需的临界采宽,岩体未发生破坏。垮落后,岩体充填采空区,岩体内应力达到新的平衡。

(2)垮落带发育阶段。随着工作面的持续向前推进,直接顶板岩体不断垮落,直至工作面开采结束。在模型向前推进到70 cm时(对应实际开采距离140 m),垮落带升高到3.8 cm,此后垮落带只在横向上发展,其竖向垮落高度保持不变。

(3)裂隙带发育阶段。伴随着垮落带的发育,其上部形成悬空,当悬空距离超过上覆砂岩破裂的临界限度时,砂岩面出现破断,由于下伏垮落带的支撑作用,在煤柱两侧出现折断,形成类似铰接的结构。在工作面推进至50 cm(对应实际100 m)时,裂隙带初次出现,并随着工作面的推进快速向上发育。当推进至90 cm(对应实际180 m)裂隙带发育至煤层上方18 cm(包含垮落带)处,随着采动的持续进行,在横向上持续扩张。随着下伏采空区面积扩大,垮落岩体被上覆裂隙带岩体逐步压实,而裂隙带高度不再向上发育,裂隙带与上覆岩层局部出现离层。

(4)覆岩移动变形阶段。随着采动距离增大,裂隙带与上覆岩层产生的离层也在上覆岩层的弯曲变形中逐渐闭合。至工作面采长180 cm时,采空区中部产生的离层基本闭合,仅剩局部横向裂缝。在工作面开采结束后,并未对模型架进行拆除,持续观察覆岩(土)层在其自重作用下的缓慢变形发育。并对地表及覆岩移动变形继续进行观测,直至变形稳定,位移基本不再发生大的变化。

最终形成的垮落带高度约为3.8 cm(相当于实际7.6 m),裂隙带高度约为14.2 cm(相当于实际28.4 m)。经计算,模型的垮采比为3.5,裂采比为12.9。

3.2 地表及覆岩移动变形规律

矿井工作面推进到一定距离后,采空区所造成的岩移便波及地表,使工作面上方地表因采动而发生水平向及竖直向移动,形成范围较工作面更大的下沉盆地。

通过在模型地表及各覆岩层设置位移测点,架设百分表,对地表及覆岩移动变形进行观测。统计汇总移动变形数据并绘制成曲线(图3、图4),可较完整地呈现地表及覆岩(土)层在开采过程中的动态移动变形规律。

3.2.1 地表移动变形规律

经测量结果反映出的采动过程中各阶段地表的移动变形情况如图3所示,由此地表移动变形规律如下。

(1)最大下沉值基本位于采空区中央,下沉曲线沿中央中线大体上呈对称分布;且随着工作面向前推进,采动距离的扩大,下沉值呈快速增长,其地表下沉影响范围也逐渐扩大,最大下沉值也随着工作面的推进不断沿着开采方向前移。水平移动曲线沿着采空区中央呈现反对称,峰值基本处于矿柱上方地表处;且水平移动值的零点基本位于采空区中央区域,因采空区中央地表总体上只发生竖向的下沉,在水平方向移动量较小或不移动;随着工作面的推进,水平移动值的零点也随着工作面前移,左侧峰值位置保持不变,仅随着开采距离的增大而数值增加,右侧的反向峰值位置及数值,随着工作面推进不断增大且前移。

(2)根据测得的下沉值及水平移动值,通过倾斜和曲率变形的计算公式进行计算,获得倾斜和曲率变形曲线[图3(c)、图3(d)]。由倾斜变形曲线知,地表的倾斜变形与水平移动曲线呈现类似规律,都表现为沿着采空区中央呈反对称的趋势,且右侧反方向倾斜值随着采动推进增大前移。由图3(d),地表曲率在推进至100～300 m时出现3个峰值,分别为位于两侧煤柱上方的两个正曲率峰值以及位于采空区中央的负曲率峰值;当工作面推进至400 m时,曲线上仍是两个正曲率峰值,分别位于两侧煤柱上方,而在负曲率部分,相较于前300 m开采,负曲率峰值有所减小,呈现波动状态。

(3)随着采动距离增大,地表盆地的影响范围也在不断扩大,地表最大下沉值、水平移动值、倾斜变形、曲率变形也逐渐增大,影响较为集中,收敛较缓慢,边界处下沉趋势仍较平缓。

3.2.2 不同层位覆岩移动规律

通过对不同层位的移动变形观测,获得终采阶段地表及覆岩层的移动变形曲线(图4),由此探索覆岩和地表的变形规律。

(1)通过对不同推进阶段各层位的下沉曲线[图4(a)、图4(b)]分析知,竖向下沉值随着覆岩深度的增大而增大,最大值均位于不同推进阶段的采空区中央附近,呈对称分布;各阶段下沉值在煤柱上方收敛较快,位于煤柱一侧的下沉值随着深度的增大而略有减小,主要由于采空区影响范围类似于碗状结构,随着距地表深度的增大,该区域位于地表边界点与采空区边界的连线外侧,加之下方煤柱的支承作用,导致煤柱上方下沉值随埋深增大而略有减小。随着工作面的推进,地表及覆岩下沉值逐渐增大,且下沉曲线的形状也由V字形变为类似U形。

(2)由于存在厚松散层,可观测到不同松散层厚度处的移动变形情况,由图4(b)可知,随着测线越靠近地表,松散层厚度越大,下沉曲线越平缓,且影响范围越大。这一现象也反映出在煤层开采过程中上覆厚松散层呈倒梯形下沉。

(3)由倾斜变形曲线[图4(c)]与水平移动曲线[图4(e)]可知,不同埋深的水平移动曲线及倾斜变形曲线呈现相似的规律,两者均沿着采空区中央呈反对称,同时有一正一负两个峰值,在采空区中央附近的水平移动值较小,贴近于零值线。不同层位的水平移动值的极值均位于采空区煤柱上方附近,且随着深度的增加,移动值减小;由于基岩层移动角大于松散层移动角,加之该研究区松散层较厚,地表水平移动变形值最大值偏向煤柱边界外侧,而地表下180 m处覆岩水平移动最大值偏向工作面上方。

(4)图4(d)、图4(f)为曲率变形及水平变形曲线,两者趋势大致相同,沿采空区中心轴线呈对称分布,在煤柱上方出现最大值,随着距地表深度的增大而增大,在采空区上方区域,两者均回归零值线附近,这是由于充分采动下地表及覆岩出现平底,故曲率及水平变形均在零值线上下徘徊。

通过对不同层位下沉值及水平移动值进行统计,综合下沉曲线,通过式(1)、式(2),对此刻各层位的下沉系数及水平移动系数进行计算。计算结果如表2所示。

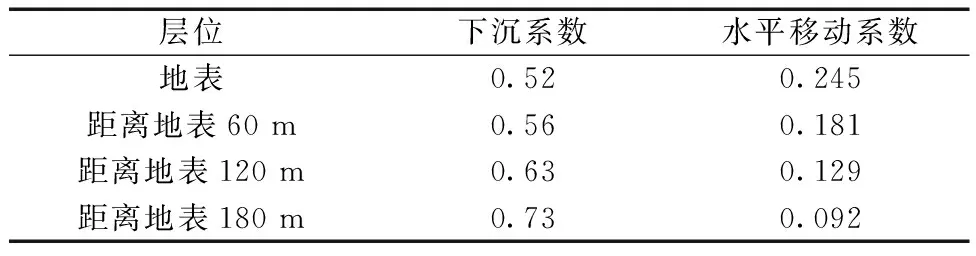
表2 不同埋深下下沉系数及水平移动系数Table 2 Subsidence coefficient and horizontal movement coefficient of different burial depths

(1)

(2)

式中:q为下沉系数;W为下沉值;M为采厚;α为煤层倾角;b为水平移动系数;U为水平移动值。

3.2.3 地表持续移动变形规律

停采后继续通过百分表对地表下沉进行观测,持续观测时间以地表下沉移动变形期结束、残余变形期开始作为最终的观测时间点,即一般情况下以6个月内下沉值不超过30 mm为界限或下沉速度v<0.167 mm/d。对停采后不同时间的百分表数据进行统计,绘制持续下沉曲线(图5),从图5可以看出,停采后地表仍产生较大下沉位移。在持续下沉阶段,采空区中央附近下沉值较大,在边界处由于煤柱的支撑作用,持续下沉仍有发生但相对较小,且左右两侧的持续下沉量并不完全对称,右侧区域的持续下沉量比左侧区域略大,主要由于开切眼位于左侧,起始采动中,左侧区域首先受到扰动,在后来的开采过程中已经伴随了持续下沉,故在停采后的持续观测阶段左侧区域相较于右侧区域下沉值偏小。最大下沉量接近基岩层位的下沉值,采掘后的地表持续下沉值更多来源于厚松散层受扰动后的层内压缩。

通过测点对地表水平移动分析,伴随着地表下沉值的增大,水平移动值也缓慢增大,监测得到地表移动变形参数如表3所示。

4 结论

依托研究区煤矿地质原型,采用模型试验,研究了厚松散层下煤层采动过程中地表及覆岩的移动变形规律。得出如下结论。

(1)通过对地表及不同埋深下地层的下沉及水平移动值对比,随着埋深的增加,采空区中央区域的下沉值不断增大,厚松散层在煤层开采过程中,随着基岩顶板的垮落、弯曲,松散层呈现倒梯形下沉,随着松散层厚度的增大,下沉曲线更加平缓、下沉值减小、影响范围增大;水平移动值在煤柱上方随着深度的增大而减小,距离顶板较近的层位水平移动最大值偏向工作面上方,而非煤柱正上方;下沉系数随着埋深增大而增大,水平移动系数随着埋深增大而减小。在煤层采厚2.2 m条件下,观测获得地表的最大下沉值为1 447.6 mm,最大水平移动值为394.6 mm。

(2)松散层的移动变形是基岩下沉与松散层压缩叠加造成的,在采掘结束后的持续变形阶段,松散层压缩导致的移动变形值在整体移动变形上占比增大;基岩层的移动变形主要受煤层开采的影响,整体呈正梯形。厚松散层矿区的下沉盆地更加平缓,影响范围更大,厚松散层的缓慢压缩致使残余下沉时间更长。

(3)对覆岩破坏规律进行分析,可将覆岩破坏分为4个阶段:初次垮落阶段,垮落带发育阶段,裂隙带发育阶段,覆岩稳定变形阶段;观测获得垮落带与裂隙带高度分别为7.6 m和28.4 m,垮采比3.5,裂采比12.9。

(4)通过对开采后的模型持续观测,地表的持续变形呈现出采空区中央附近持续下沉较大,水平移动值伴随着厚松散层在自重作用下的压缩不断增大,但整体发育缓慢,监测结果可获得其移动变形基本指标的量化值。