含腐蚀缺陷管道拉伸应变能力预测模型研究

余志峰, 田宏军, 赵前坤, 曹宇光*, 刘媛媛

(1.中国石油天然气管道工程有限公司, 廊坊 065099; 2.中国石油大学(华东)储运与建筑工程学院, 青岛 266000)

作为主要的运输油气资源设备,长输管道的安全性显得尤为重要。现役管道一般处于地下或者海底,而埋藏环境的复杂性使得管道易受到腐蚀[1-2],极端的地理条件也会带给埋地管道更多形式的安全威胁,如地震、滑坡、土地冻胀或者融化沉降等灾害导致地面移动,从而对埋地管道造成较大的轴向变形[3-4]。然而,一些学者发现基于应力评估对土体移动下埋地管道的安全评价过于保守[5-7],随着管线钢性能的提升,基于应变评估在地质灾害地段管道的安全评价中逐渐得到利用。目前已有部分规范对应变评估进行规定,如ManualforDeterminingtheRemainingStrengthofCorrodedPipelines(ASME B31G—2012)[8]、OilandGasPipelineSystems(CSA Z6620—2015)[9]和CorrodedPipelines-RecommendedPractice(DNV RP-F101—2013)[10]等。基于应变评估的关键目标为确保管道不丧失完整性的同时能够维持土体移动引起的塑性变形。

拉伸应变能力(tensile strain capacity, TSC)是指管道在不丧失完整性下的极限拉伸应变水平,它在应变失效评估中至关重要,因为其可以直接与管道拉伸断裂联系在一起。在役管道的完整性评估通常涉及具有腐蚀缺陷的管段。然而,关于腐蚀管道TSC的研究十分有限,许多研究都集中于环焊缝管道的拉伸断裂和腐蚀管道的压缩屈曲。Tang等[11]基于模拟延性开裂的GTN(Gurson-Tvergaard-Needleman)模型,通过裂纹尖端张开位移确定含裂纹管道的TSC,并基于参数有限元分析结果拟合TSC预测方程。Smith等[12]通过实验和有限元分析研究了腐蚀管道的屈曲失效,并预测了失效时的极限弯矩和管道挠度。Dewanbabee[13]研究了腐蚀缺陷尺寸和内压等因素对轴向压缩载荷下腐蚀管道褶皱形成的影响,随后对弯曲载荷和内压联合作用的腐蚀管道进行参数敏感性分析。目前亟需开发一个适用于腐蚀管道的TSC预测方程以快速评估应变设计地段腐蚀管道的拉伸应变能力。

鉴于此,首先建立腐蚀管道TSC数值计算模型,并将其计算结果与全尺寸管道拉伸试验测试结果进行对比,验证数值模型的准确性。随后,利用参数有限元分析,研究腐蚀缺陷尺寸(深度,宽度和长度)和管道尺寸(外径和壁厚)对TSC的影响。最终,根据输入参数对TSC的影响规律构建了具有合理形式的预测方程,结合有限元结果拟合一个能够预测腐蚀管道TSC的封闭式方程,为基于应变设计地段腐蚀管道的完整性评估提供参考。

1 全尺寸管道拉伸实验

Zhou等[14]基于液压控制加载系统开展了全尺寸管道拉伸实验以研究拉伸应变能力。实验材料为X70管道,其管道外径D为324 mm,管道壁厚t为7.14 mm。管道外壁表面加工“均匀盒状缺陷”(腐蚀深度d、腐蚀宽度W和腐蚀长度L),腐蚀缺陷的几何特征如图1所示。实验过程分为两个加载阶段:第一阶段,对管道施加内压直至管体的环向应力达到72%的管材最小屈服强度;第二阶段,通过固定端夹具对管道施加轴向拉伸载荷直至其破裂。此外,实验管道的0°、90°、180°和270°轴线安装了位移传感器与应变计,具体的铺设位置如图2所示。管道发生断裂时,通过4个1D位移传感器和数字图像相关(digital image control, DIC)仪器测量距离管道中心1D～2D的平均轴向应变,并将其平均值作为TSC。C-FER公司总共进行3组含不同腐蚀缺陷的管道拉伸试验,每个腐蚀缺陷的尺寸如表1所示。

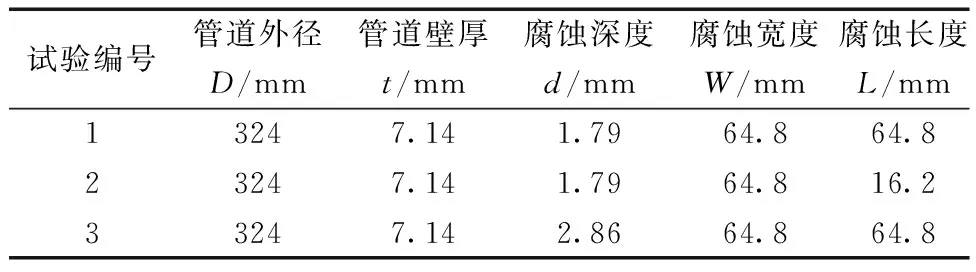
表1 全尺寸管道拉伸实验中的腐蚀缺陷尺寸Table 1 Dimensions of corrosion defects in full-size pipe tensile tests

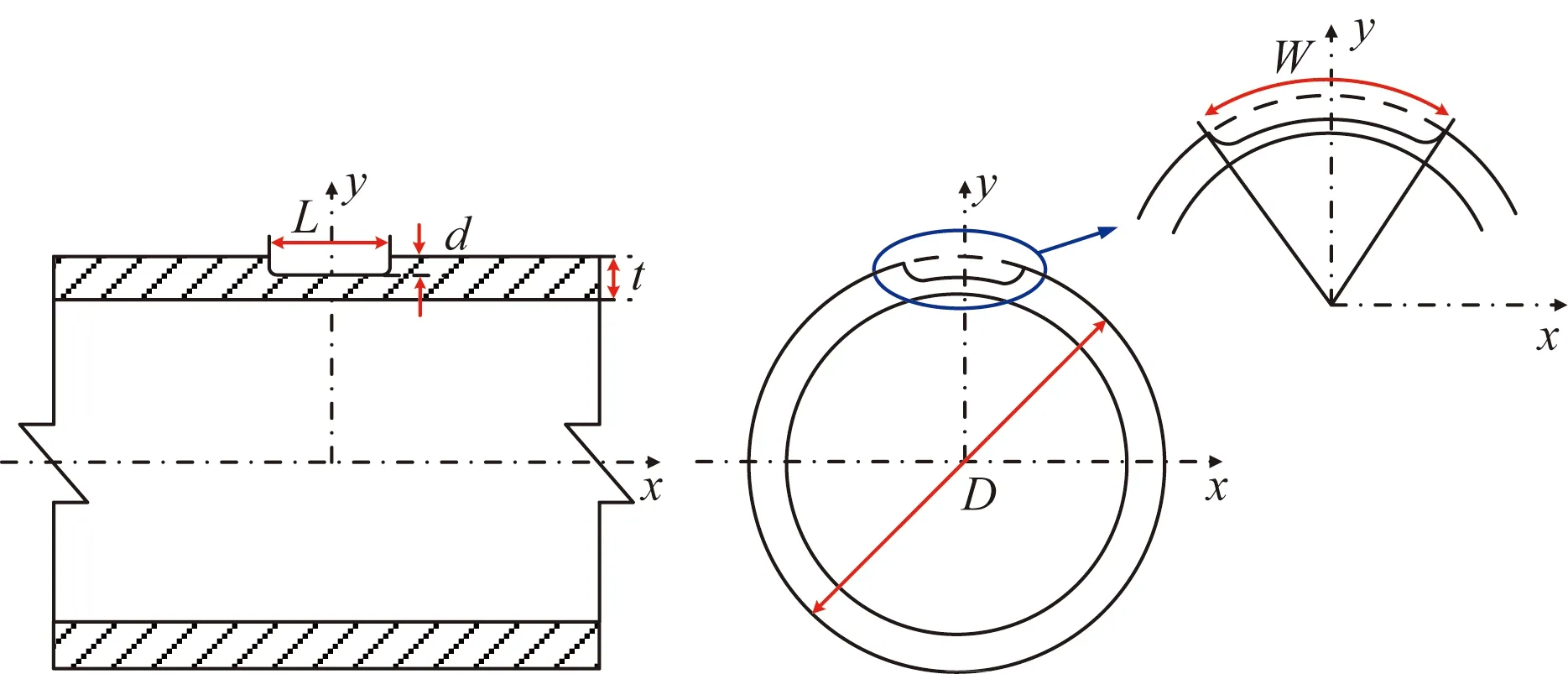
图1 腐蚀缺陷几何特征Fig.1 Geometric characteristics of corrosion defects

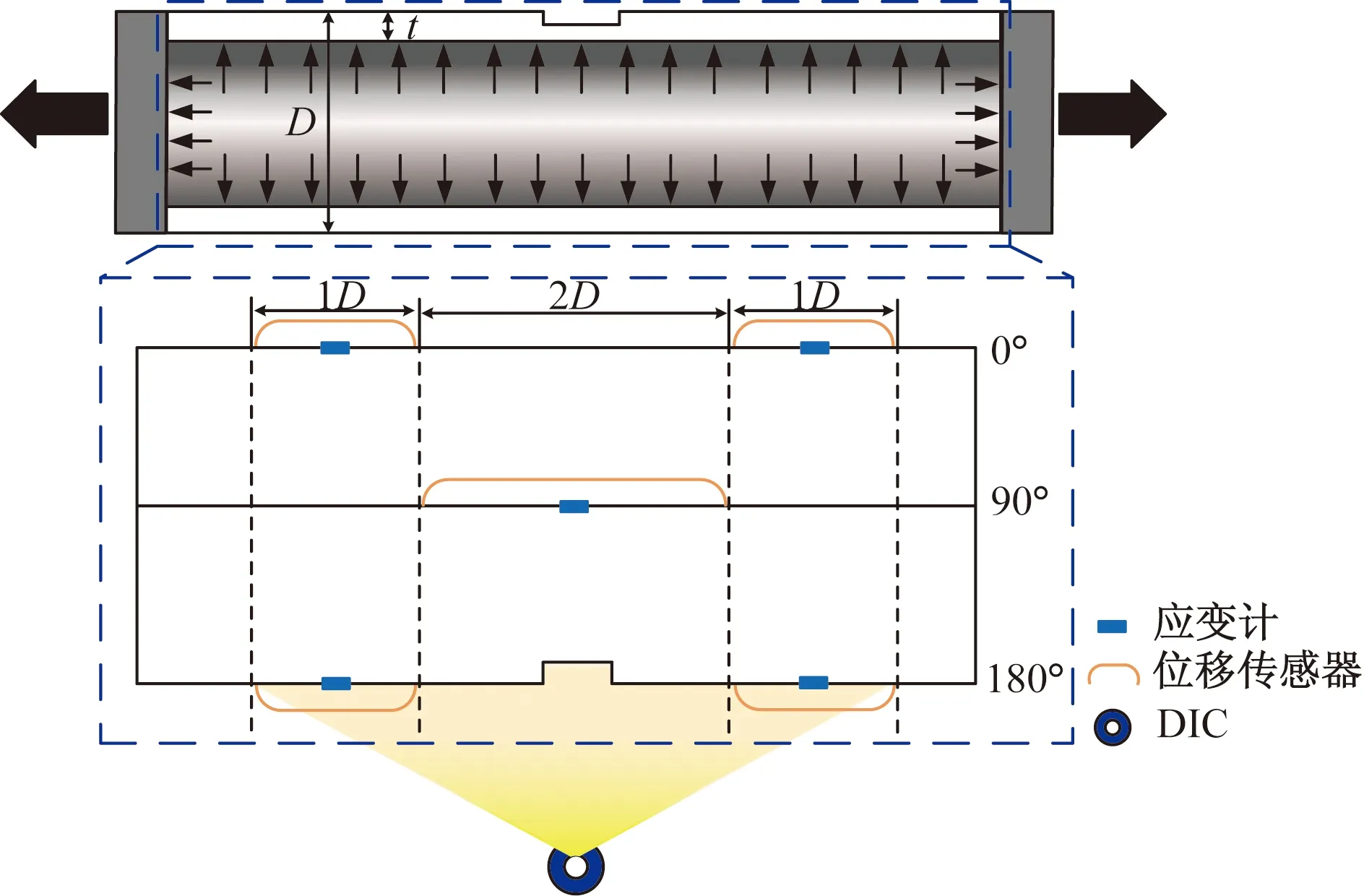
图2 全尺寸管道拉伸试验示意图Fig.2 Schematic diagram of full-size pipe tensile experiment

2 TSC有限元计算方法及验证

2.1 有限元模型

对全尺寸管道实验进行有限元分析以验证腐蚀管道TSC的数值计算方法。为了简化模型的网格数量,根据几何结构的对称性建立1/4腐蚀管道模型,模型的3个对称截面施加对称约束。在管道右端的截面中心布置一个参考点,并建立此管端截面与参考点的耦合,以实现轴向拉伸载荷的施加。考虑到几何结构与材料的非线性,单元类型采用高阶三维20节点的实体单元。为了平衡计算的效率和精度之间的矛盾,将腐蚀缺陷及其附近区域网格细化,距离腐蚀缺陷较远的区域划分地相对稀疏。遵循BSI 7910的建议,腐蚀缺陷的剩余韧带沿壁厚方向划分为4层单元。网格模型的最小和最大的单元尺寸分别为3 mm×3 mm和30 mm×20 mm,单元总数量在65 000～75 000。腐蚀缺陷管道有限元模型及参考点的耦合方式如图3所示。

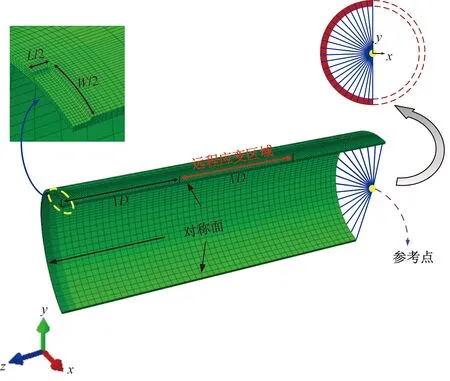
图3 1/4腐蚀管道有限元模型Fig.3 The 1/4 finite element model of the corroded pipeline

遵循试验的加载方式,有限元中的加载通过两个分析步进行:在第一分析步中,对管道模型的内表面施加压力,同时考虑施加内压后的端盖效应[15],即对端部界面上的所有节点施加等效的轴向应力;在第二分析步中,对参考点施加轴向位移载荷以拉伸整个管体,直至其失效,整个拉伸过程中的内压保持恒定。

2.2 材料模型

模拟计算时,假设管线钢材料服从各向同性硬化的塑性流动准则。管线钢的真实应力-应变关系可以通过Ramberg-Osgood模型描述为

(1)

式(1)中:σ和ε分别为真实应力和真实应变;σy为管线钢的屈服强度;E为弹性模量;α和n为与材料应变硬化相关的常数。

基于Masayuki[16]提出的经验关系,R-O本构方程中的α和n可以通过管线钢的屈服强度σy和抗拉强度σb估算为

(2)

式(2)中:εpy为材料达到屈服时的塑性应变,取0.2%。

(3)

全尺寸管道试验中X70管线钢的屈服强度为573 MPa,抗拉强度为638 MPa,弹性模量为203 GPa和泊松比为0.3。

2.3 失效准则

在有限元中,腐蚀管道的TSC定义为拉伸载荷下管道失效时的极限远程应变,即容许拉伸远程应变[17]。为了获得相对稳定的轴向应变,需要规避腐蚀缺陷附近的应变集中和管端附近的应变波动[18]。因此,选取距离腐蚀缺陷1D～2D的远程应变区域(图3红色标记区域)以计算腐蚀管道的TSC。

RecommendedPracticeforFitness-for-service(API 579—2020)[19]中提供了基于应力修正临界应变的局部失效准则,即当最大等效塑性应变达到临界应变时管道发生失效,该准则适用于评估具有缺陷结构的完整性。RecommendedPracticeforFitness-for-service(API 579—2020)给出通过应力三轴度表征临界应变的经验关系式,可表示为

(4)

式(4)中:εf为临界应变;σm和σeq分别为平均应力和等效应力,σm/σeq为应力三轴度;εLu、m2和αsl为需要确定的材料常数。

参考Kim等[20]通过缺口圆棒拉伸试验和有限元分析确定的材料参数,计算出X70管线钢的临界应变εf为1.66。式(4)中具体的材料参数如表2所示。

表2 X70管线钢临界应变的材料参数Table 2 Material parameters of critical strain of X70 pipeline steel

2.4 模型验证

根据图4所示的腐蚀管道失效时轴向应变云图与实际腐蚀缺陷断裂形貌[17]的对比结果可知,与试验对应的3根管道失效时轴向应变集中位置均接近实际断裂位置,表明数值模拟结果具有合理性。图5为有限元计算的TSC与实验测试值的对比结果,可以看出,TSC数值计算值与实测值之间的最小误差为4.41%,最大误差为9.24%,两者相近且符合模拟精度,验证TSC数值计算方法的准确性。此外,针对试验1号管道,提取模型的最大等效塑性应变和远程应变数据,且采用RecommendedPracticeforFitness-for-service(API 579—2020)确定TSC。根据图6所示的最大等效塑性应变随远端应变的变化曲线可知,最大等效塑性应变始终增大,而远端应变先增大后减小,管体的最大远端应变确定为2.33%。通过应变失效准则确定的TSC为2.19%,其与管体的最大远端应变在数值上接近,进一步验证了TSC数值计算方法的可靠性。

图4 轴向应变云图与实际断裂形貌的对比结果Fig.4 Comparison results between axial strain nephogram and actual fracture morphology

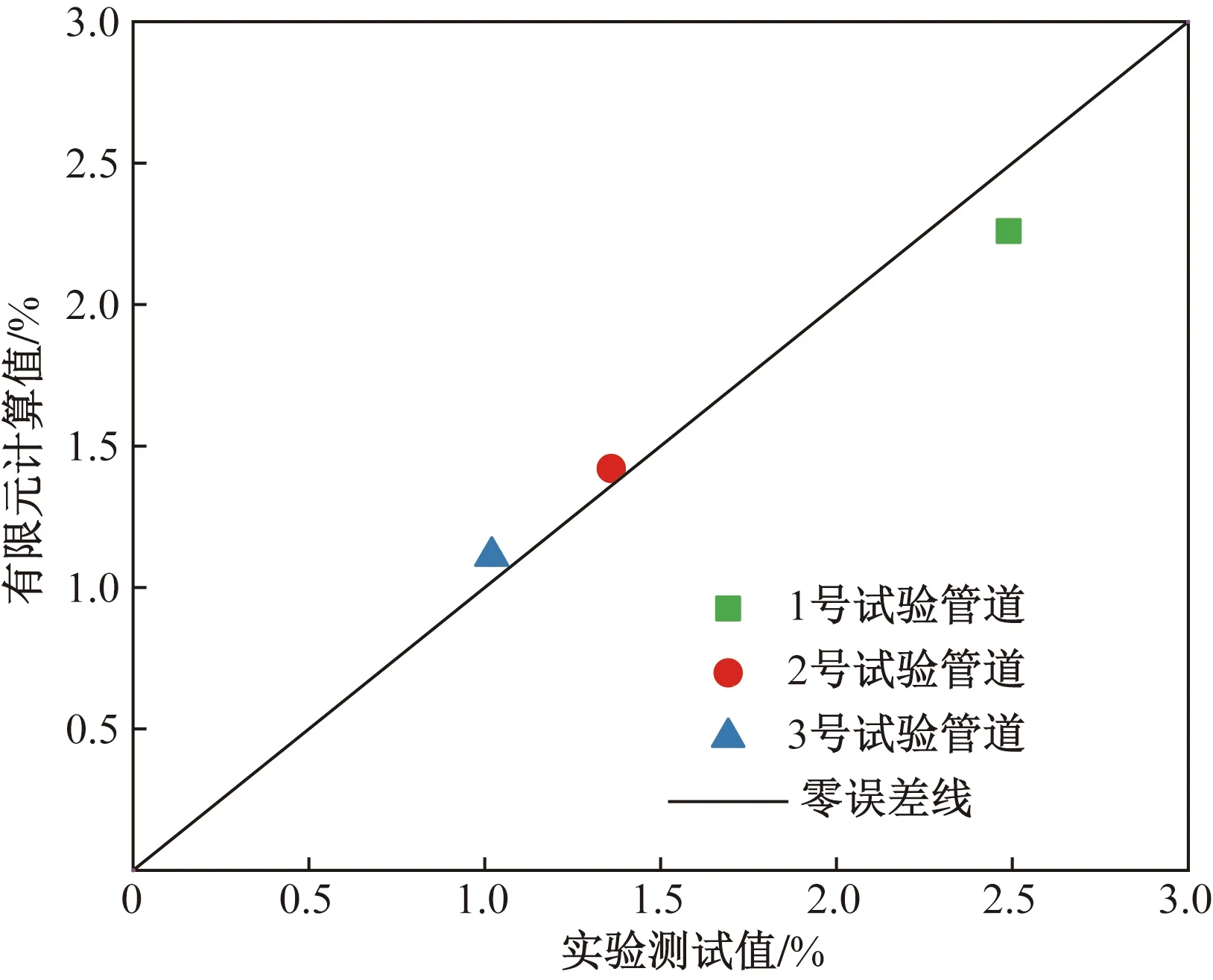
图5 有限元计算值与实验测试值的对比结果Fig.5 Comparison results of finite element calculationvalues and experimental test values

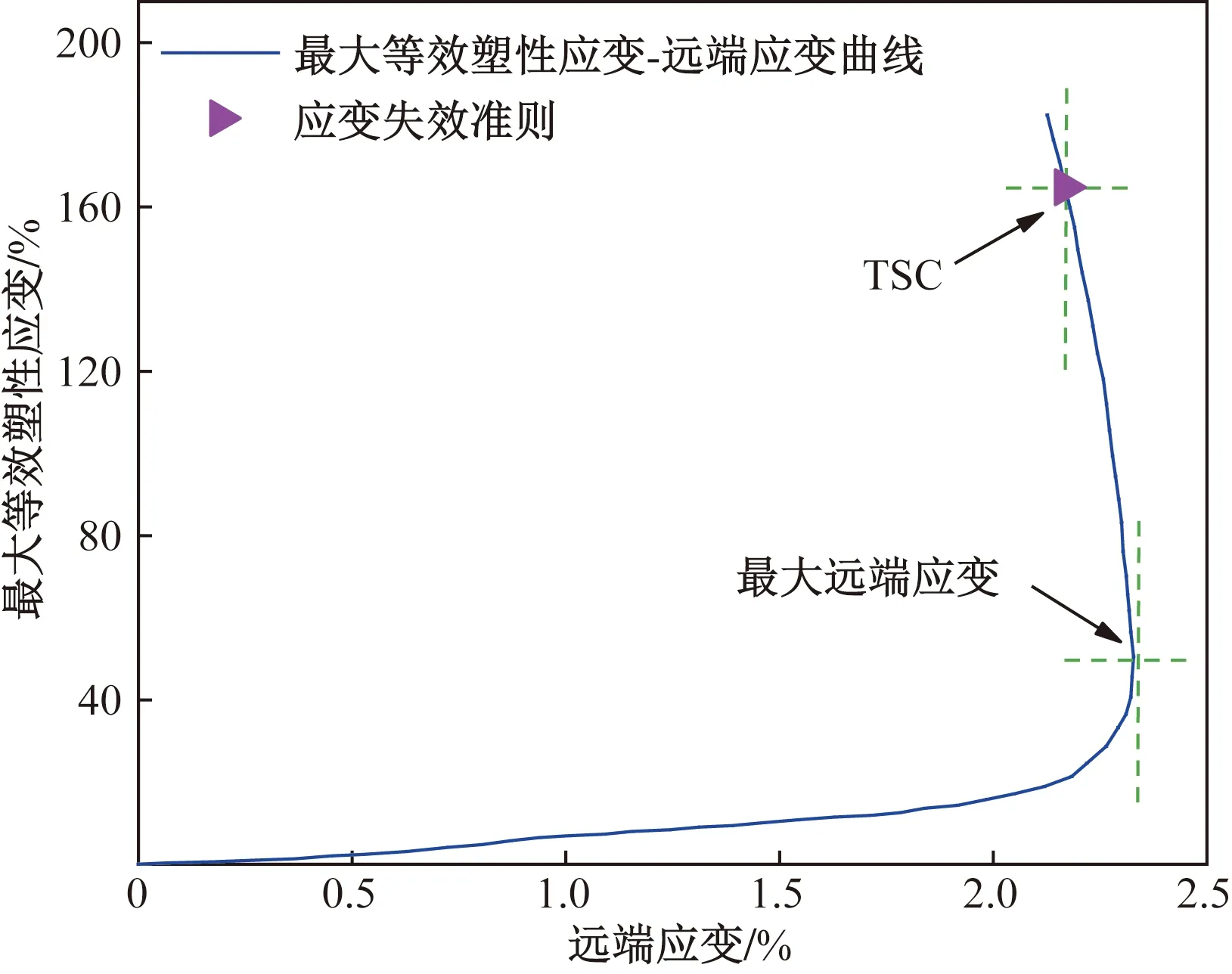
图6 最大等效塑性应变与远端应变的关系Fig.6 Relationship between maximum equivalent plastic strain and remote strain

3 参数有限元分析结果

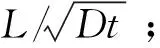
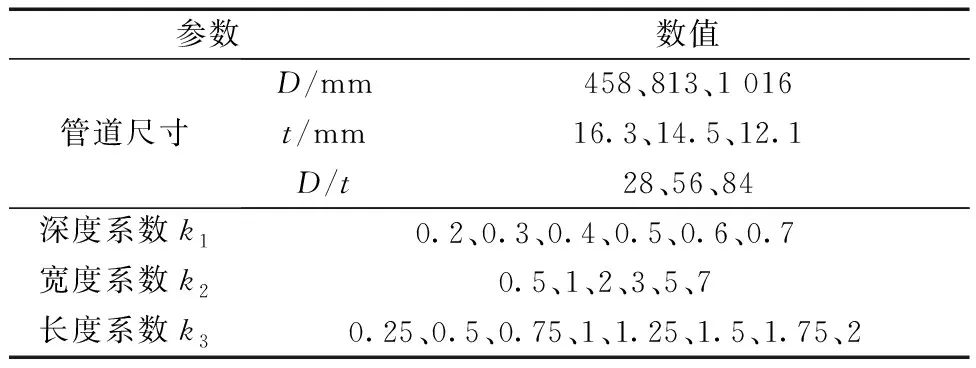
表3 TSC数值计算参数Table 3 TSC numerical calculation parameters

3.1 腐蚀深度的影响

根据不同腐蚀深度管道在失效时的轴向应变云图(图7)可知,对于k2=2,k3=1的腐蚀缺陷,当腐蚀深度系数k1=0.2时,应变集中在距缺陷中心36.12 mm处;随着k1增加到0.7,应变集中位置仅向轴向边缘移动2.01 mm,表明腐蚀管道发生拉伸断裂的位置与腐蚀深度无关。此外,随着k1从0.2增加到0.7,最大轴向应变从27.54%增加到93.11%,而TSC从1.98%下降到0.79%,表明腐蚀深度的增加会加剧轴向应变向腐蚀区域集中,从而使TSC降低。

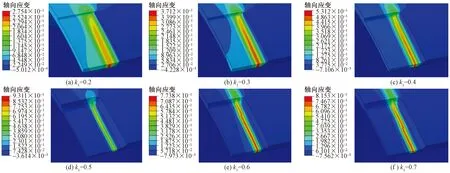
图7 不同腐蚀深度管道失效时刻轴向应变云图Fig.7 Axial strain nephograms of pipeline with different corrosion depths at the failure moment

根据图8所示的腐蚀宽度一定(k2=2)时拉伸应变能力(tensile strain capacity, TSC)随腐蚀深度的变化曲线可知,TSC随腐蚀深度的增加而明显下降,且TSC关于腐蚀深度系数k1呈非线性负相关。对于k2=0.04,k3=1的腐蚀缺陷,随着k1从0.2增加到0.7,TSC从1.71%下降到0.52%,下降幅度为69.59%。结果表明,腐蚀深度是影响腐蚀管道抵抗拉伸断裂的重要因素,腐蚀深度的增加会降低腐蚀管道的局部强度。

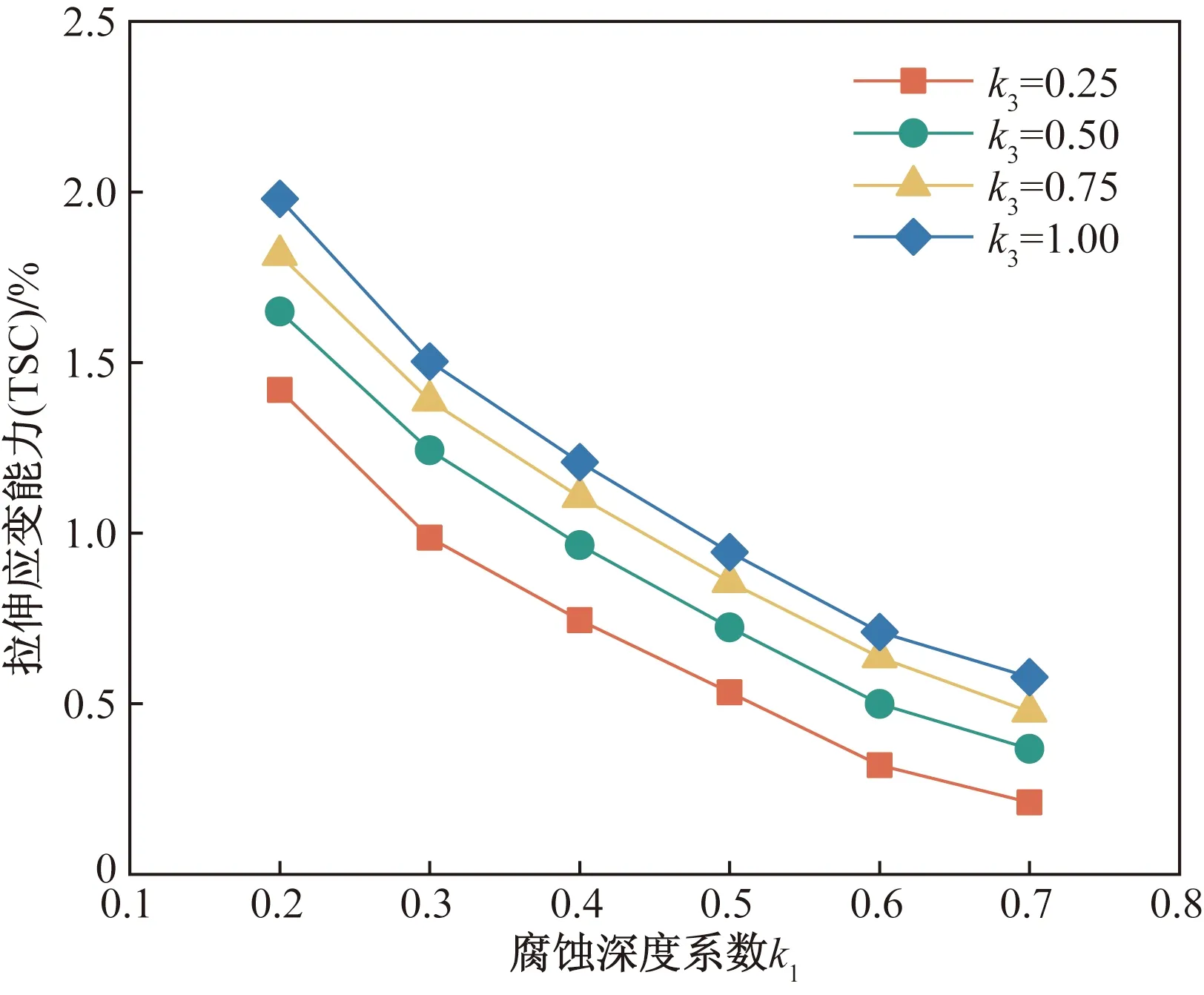
图8 TSC随腐蚀深度的变化Fig.8 Variation of TSC with corrosion depth

3.2 腐蚀宽度的影响

根据图9不同腐蚀宽度管道在失效时的轴向应变云图可知,对于k1=0.3、k3=1的腐蚀缺陷,当腐蚀宽度系数k2=0.5时,应变集中在距缺陷中心41.96 mm处;随着k2增加到7,应变集中位置仅向缺陷中心移动3.76 mm,表明腐蚀宽度几乎不影响腐蚀管道发生拉伸断裂的位置。随着k2从0.5增加到7,最大轴向应变从31.27%增加到60.61%,而TSC从3.74%下降到0.60%。与腐蚀深度的作用相同,腐蚀宽度的增加会加剧轴向应变向腐蚀区域集中,从而降低TSC。

根据图10所示的腐蚀长度一定(k3=1)时TSC与腐蚀宽度的关系可知,TSC随着腐蚀宽度的增加而减小。对于k1=0.4,k3=1的腐蚀缺陷,当腐蚀宽度系数k2=0.5时,TSC为2.25%,随着k2增加到7,TSC下降到0.25%,下降幅度为88.89%。TSC随腐蚀宽度的变化曲线均具有非线性特征,表现为随腐蚀宽度的增加,TSC在k2≤3时减小得更快;当k2达到3时,k1为0.5、0.6和0.7的3条TSC随腐蚀宽度系数的变化曲线几乎重叠,这是因为壁面发生了大量的金属损失,管道的承载能力不足以抵抗内压。因此,基于应变的评估不能应用于过于大深度和宽度的腐蚀缺陷。在后续预测方程的拟合中,不考虑TSC低于0.2%的情况。

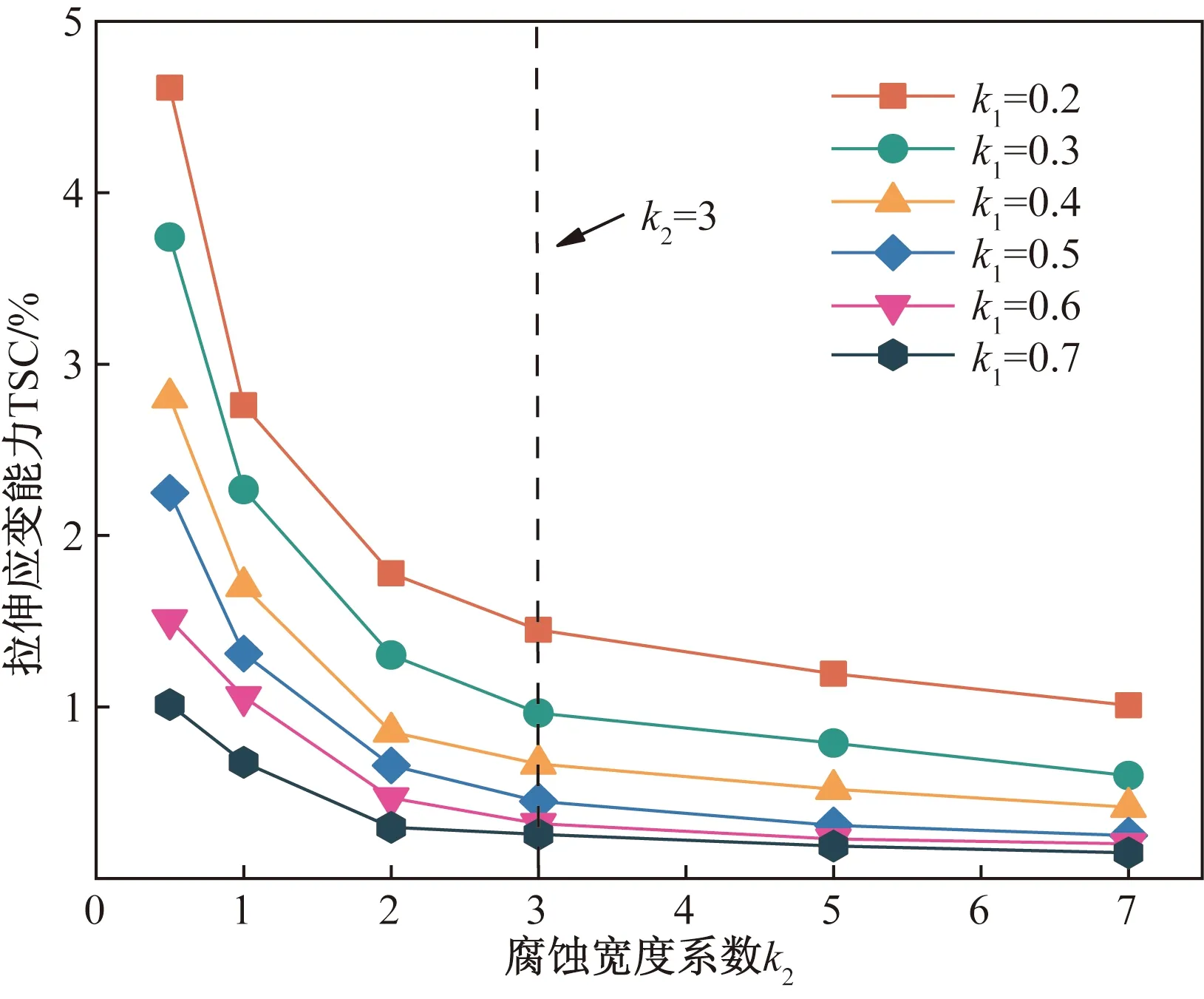
图10 TSC随腐蚀宽度的变化Fig.10 Variation of TSC with corrosion width

3.3 腐蚀长度的影响

研究表明,只有短腐蚀缺陷才会影响腐蚀管道的应变能力,而临界腐蚀长度尚未被明确[14]。鉴于此,对腐蚀长度系数k3≤2的不同腐蚀管道进行数值建模。根据图11所示不同腐蚀长度管道在失效时的轴向应变云图可知,当k1=0.3,k2=1时,随着k3从0.25增加到1,应变集位置从腐蚀区域的中部移动到75.76%(距腐蚀中心距离/腐蚀缺陷长度)处,当k3继续增加到2时,应变集中位置移动到腐蚀区域的77.75%处。结果表明,腐蚀长度在k3≤1时影响腐蚀管道发生拉伸断裂的位置。这是因为腐蚀长度的增加导致剩余韧带横截面上的力中心发生偏移,从而使弯曲应力发生变化。随着k3从0.25增加到1,最大轴向应变从61.24%下降至42.81%,而TSC从1.31%增加到2.29%;当k3继续增加到2时,最大轴向应变仅下降至42.39%,而TSC增加至2.36%。结果表明,当k3≤1时,腐蚀长度的增加才会缓解轴向应变向腐蚀区域集中,从而使TSC上升。

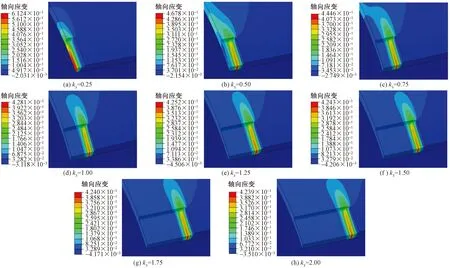
图11 不同腐蚀长度管道失效时刻轴向应变云图Fig.11 Axial strain nephograms of pipeline with different corrosion lengths at the failure moment

图12为腐蚀缺陷管道TSC随腐蚀长度的变化情况。根据图12(a)所示的腐蚀深度一定(k1=0.3)时TSC与腐蚀长度的关系可知,当k3≤1时,腐蚀管道TSC随腐蚀长度的增加而线性增加。这是因为腐蚀长度的增加降低了缺口效应,从而增强了管道的塑性变形性能。当k3达到1后,TSC随腐蚀长度的变化曲线趋于水平,表明TSC与腐蚀长度无关。由图12(b)可以看出,TSC随腐蚀长度变化的规律(k1=0.5)与图12(a)中获得的结果(k1=0.3)相似,且腐蚀长度对TSC的影响存在一个相同的临界值,即k3=1。根据以上结果得出结论,腐蚀长度对TSC的线性增强作用只发生在k3≤1时。

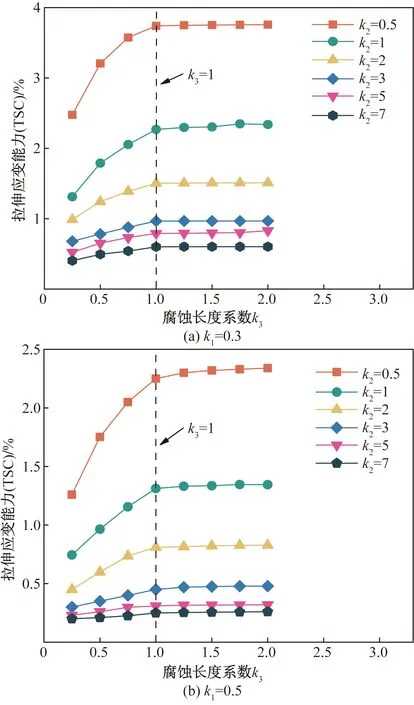
图12 TSC随腐蚀长度的变化Fig.12 Variation of TSC with corrosion length

3.4 径厚比的影响

分别建立径厚比为28(D=458 mm,t=16.3 mm),56(D=813 mm,t=14.5 mm)和84(D=1016 mm,t=12.1 mm)的X70管道,以研究管道尺寸对TSC的影响。在管道外表面建上不同尺寸的腐蚀缺陷,径厚比对TSC的影响如图13所示。可以看出,TSC随着径厚比的增大变化地很小。例如,对于腐蚀尺寸为k1=0.3,k2=2和k3=1的管道,随着D/t从28增加到56,TSC从1.59%下降到1.51%,当D/t继续增加到84时,TSC仅下降到1.47%,结果表明TSC与管道径厚比无关。

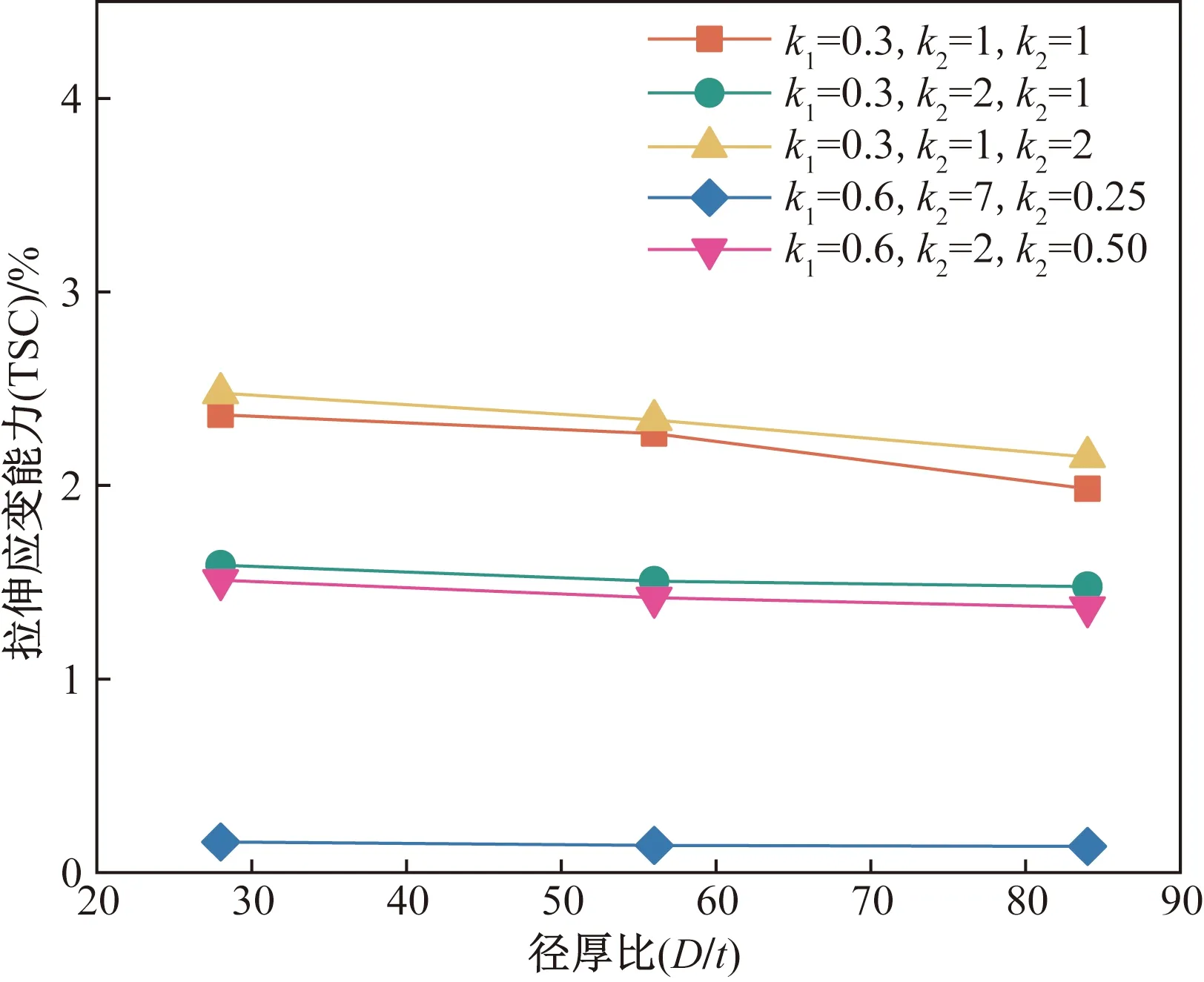
图13 TSC随径厚比的变化Fig.13 Variation of TSC with diameter-to-thickness ratio

4 TSC预测方程的拟合及验证

为了拟合一个能够预测腐蚀管道TSC的封闭式方程,笔者收集了198个数值算例中TSC大于0.2%的185个算例。由于管道的径厚比(D/t)对TSC几乎不存在影响,未将其纳入预测方程。TSC作为一个关于腐蚀深度系数k1(0.2≤k1≤0.7)、腐蚀宽度系数k2(0.5≤k2≤7)和腐蚀长度系数k3(0.25≤k3≤2)的函数。在方程推导中,需要选择具有适当函数依赖性的方程形式,以保证TSC与输入参数之间的相关性。根据参数有限元分析结果发现,TSC关于腐蚀深度系数k1和腐蚀宽度系数k2呈非线性负相关,关于腐蚀长度系数k3呈线性正相关(k3≤1)。此外,TSC预测方程需满足3个边界条件:当k1趋近于1时,TSC趋近于0;当k1=k2=k3=0时,TSC与腐蚀缺陷尺寸无关;当k3趋近于1时,TSC趋近于一个常数。因此,通过腐蚀缺陷尺寸描述的TSC方程可以假定为

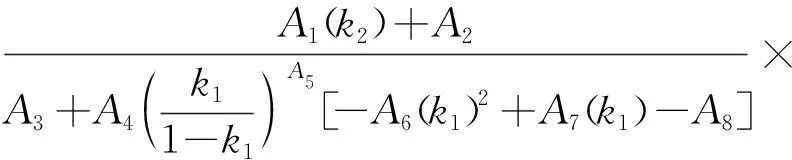
(5)

式(5)中:A1～A8为待定回归系数。

由于影响TSC的临界腐蚀缺陷长度为k3=1,需要对输入参数的范围进行2层划分。基于185个有限元结果,采用OriginLab软件包进行对式(5)进行非线性拟合,所确定的回归系数如表4所示。此外,非线性拟合中的决定系数R2为0.984 2,残差平方和为1.576 9,其验证了所构建的预测方程形式的合理性。

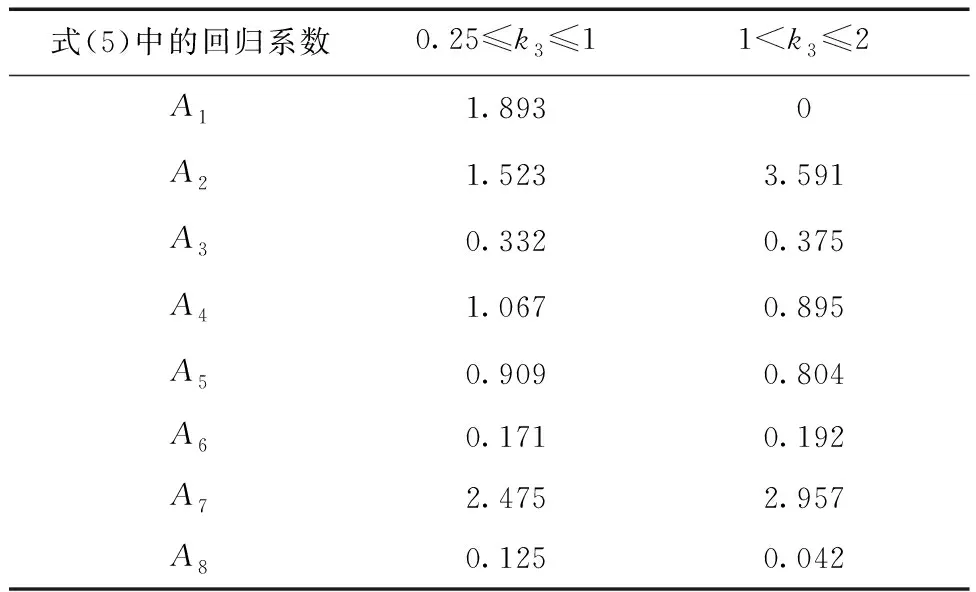
表4 式(5)所确定的回归系数Table 4 Regression coefficients determined for formula(5)

图14为采用预测方程计算的TSC和有限元结果之间的对比结果,其中45°实线代表零误差线,两条虚线代表±20%误差线。可以看出,大部分数据点均靠近0误差线,且仅有个别数据点超出±20%误差线,所提出方程与有限元法之间的TSC平均误差为5.78%,这表明两者之间拟合地较好。

图15为对185个算例采用预测方程和有限元法得到TSC比率(方程预测值/有限元预测值)的概率直方图。可以看出,TSC比率近似服从正态分布,其中82.34%算例的TSC比率处于0.9～1.1范围内,且94.17%的TSC比率处于0.8～1.2范围内,表明在这185个算例中,82.34%的预测误差小于10%且94.17%的预测误差小于20%,进一步验证了所提出方程的可靠性。

表5为TSC方程预测值与实验测试值之间的对比结果,可以看出,最小误差和最大误差分别为3.68%和24.51%,在一定程度上验证了所提出方程的准确性,较大的误差是由于数值模型无法充足考虑真实的实验条件从而导致非线性拟合结果存在偏差较大的数据。

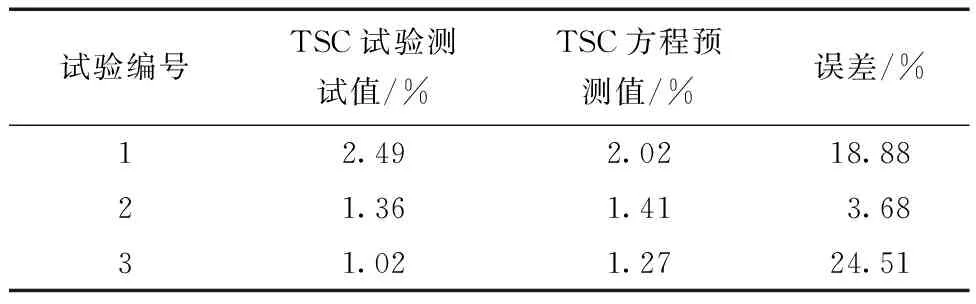
表5 方程预测值与实验测试值的对比Table 5 Comparisons of equation predicted values and experimental test values

5 结论

基于API 579应变失效准则建立了腐蚀管道的TSC数值计算模型,并通过全尺寸管道试验进行验证,随后根据参数有限元分析结果,构建一个准确且可靠的TSC预测方程,得到以下主要结论。

(1)腐蚀缺陷的深度和宽度不会影响腐蚀管道发生拉伸断裂的位置;当腐蚀缺陷长度系数k3≤1时,腐蚀长度的增加使拉伸断裂的位置从腐蚀区域的中部向边缘移动。腐蚀深度和宽度的增加会加剧轴向应变向腐蚀缺陷集中,从而使TSC下降;缺陷长度的增加会缓解轴向应变集中,从而使TSC上升。

(2)腐蚀管道的TSC关于缺陷深度和宽度呈非线性负相关;当k3≤1时TSC关于缺陷长度呈线性正相关,当k3>1时TSC不受缺陷长度的影响;腐蚀管道的径厚比几乎不影响TSC。

(3)所提出方程的形式是基于TSC与影响参数之间的相关关系建立的,因此其具有较强的预测能力。与有限元结果相比,TSC方程的平均预测误差为5.78%,误差分析结果表明,94.17%的算例的预测误差小于20%;与实验测试结果相比,TSC方程的最小和最大预测误差分别为3.68%和24.51%。事实证明所提出方程对预测腐蚀管道TSC具有准确性和可靠性。