深层水平井机械坐封过程力学精细描述
2023-12-14陈科任俊松丁亮亮梁莹
陈科, 任俊松, 丁亮亮, 梁莹*
(1.中石化西南石油工程有限公司井下作业分公司, 德阳 618000; 2.西南石油大学机电工程学院, 成都 610500)
机械坐封技术是进行油气井测试作业的重要工艺步骤,其原理为井口释放一定的悬重作用至封隔器胶筒使其径向变形,实现对油管柱内部与生产套管间的环形空间的压力封堵[1]。受水平井结构影响,测试管柱套管接触会产生摩阻;同时,测试管柱有效轴向压力超过屈曲临界载荷,测试管柱将发生屈曲变形并与套管接触使测试管柱与套管的摩阻激增。因此摩阻使井口释放的悬重不能完全传至封隔器胶筒。现场机械坐封井口悬重释放值的选取依赖经验且保守(大于等于封隔器最小压重的1.5倍),对于深层水平井,过大悬重释放值易对封隔器造成损伤,严重影响测试作业安全性。因此,开展深层水平井机械坐封过程力学研究,优化机械坐封施工参数对指导现场操作人员十分重要。
井下管柱的力学问题已被学者完成了大量的理论研究与实验分析[2]。对于井中管柱的受载问题,Johancsik等[3]首次对三维井中的管柱开展了研究,忽略管柱刚度建立了三维软杆模型。Sheppard等[4]通过实验得出模型中的摩阻系数是一个受井眼参数与泥浆影响的综合值。Ho[5]考虑了管柱刚性并建立了管柱受载的三维刚杆模型,但模型复杂求解困难。韩志勇[6]考虑了管柱与井壁不同接触状态,分别建立了井下管柱的二维与三维管柱受载模型。此后,中外学者将软杆模型与刚杆模型的考虑因素和求解算法方面进行了改进[7-10],并将模型至应用管柱的强度校核[11-12]。针对管柱的屈曲问题,Lubinski[13]首次提出了螺旋屈曲的概念,并利用能量法研究了封隔器管柱的屈曲行为,推导出了螺距与压缩力的关系公式。Paslay等[14]推导出了斜直井的正弦屈曲临界载荷。Wu[15]将管柱屈曲临界载荷以及屈曲引起的附加接触力引入管柱的整体受力模型中,建立了考虑屈曲效应的井下管柱受载模型。Mitchel[16-17]依据滑动摩擦原理,建立了含屈曲的管柱轴受载模型,并确定了管柱的屈曲长度和与井筒壁的接触载荷。文献[18-21]考虑了管柱接头以及扶正器的影响,结合钻柱的屈曲建立了管柱局部和总体受力相耦合的全管柱受载模型。练章华等[22]建立了管柱屈曲的有限元模型,分析了复杂工况下不同边界条件下的管柱的屈曲形态与横向位移,并对优化产量、设置扶正器等缓解屈曲的措施开展了评价。
虽然中外学者对井下管柱力学行为进行了大量的研究,但对深层水平井机械坐封阶段如何精准确定井口悬重值并无应用。机械坐封过程管柱端部约束条件、高垂比的水平井结构及复杂的屈曲形态让机械坐封施工参数设计变得困难。鉴于此,综合考虑井眼轨迹与管柱屈曲摩阻、及变截面影响,建立了测试管柱坐封过程的力学分析模型,为深层水平井的机械坐封悬重释放参数的设计提供了理论参考。
1 测试管柱机械坐封过程力学分析模型
1.1 模型建立
机械坐封的工作原理如图1所示。将处于井眼中的一段测试管柱(含变截面)作为一个管柱单元段i,在对其进行受力分析之前需要进行如下假设。①管柱单元的曲率为常数且管柱轴线和井眼轴线重合;②两测点间井眼轨迹位于一个空间平面内;③管柱的弯曲变形在弹性范围之内。
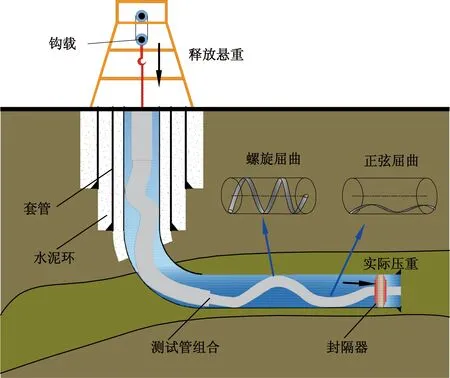
图1 机械坐封示意图Fig.1 Mechanical setting diagram
管柱单元段i的三维受力示意图如图2所示。
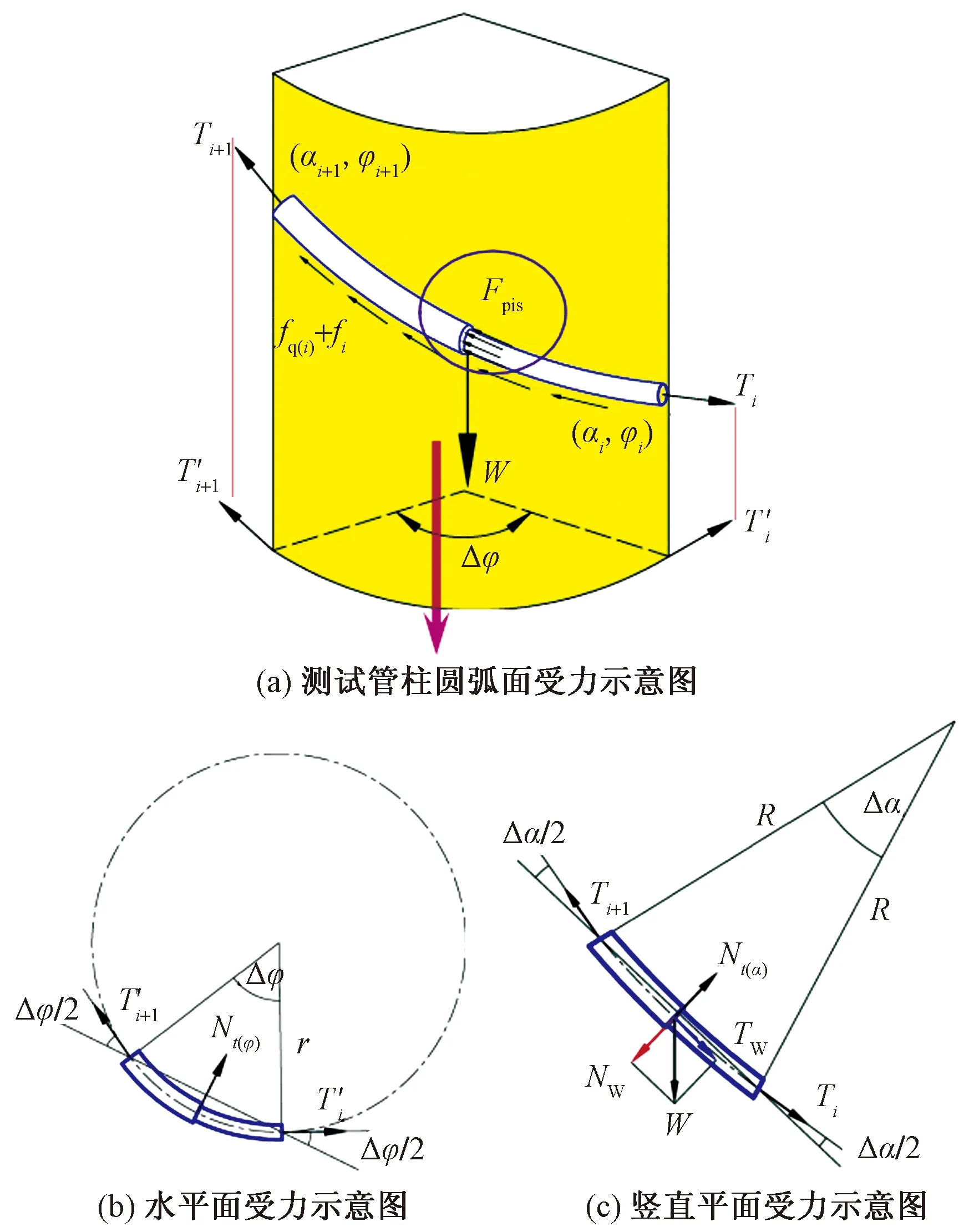
Ti、Ti+1分别为单元段管柱上、下端面真实轴向力;Fpis为变截面处的活塞力;T′i、T′i+1分别为单元段管柱的上、下端面真实轴向力在水平面的投影;αi、αi+1分别为单元段管柱上端面、下端点井斜角;φi、φi+1分别为单元段管柱上端面、下端面方位角;Δα为井斜角增量;Δφ为方位角增量;W为单元段的管柱重力;fi为管柱与套管侧向力引起的摩擦力;fq(i)为管柱与套管屈曲引起的摩擦力;R为单元段管柱在竖直平面的曲率半径;r为单元段管柱在水平面的曲率半径;TW为重力轴向分量;NW为重力法向分量;Nt(α)为侧向力在竖直平面的分量;Nt(φ)为侧向力在水平面的分量
根据圆弧面的单元管段柱受力,将单元段管柱受力分解在水平面和竖直平面随后合成并进行简化[3],最终得到管柱坐封过程的力学模型为
(1)
式(1)中:W为单元段的管柱重量,N/m;Ti、Ti+1和ΔT分别为微元段的上端点、下端点真实轴向力增量,N;αi、αi+1分别为单元段管柱的上端面与下端面井斜角,rad;Δα为井斜角增量,rad;Δφ为井方位角增量,rad;Ni、fi分别为管柱与套管的侧向力、侧向力引起的摩擦力,N;μ为管柱与套管壁的摩擦系数;Nq、fq分别为管柱与套管的屈曲接触力、屈曲摩阻力,N;L为单元段管柱的长度,m。
当管柱发生屈曲变形之后,管柱将进一步与井壁或套管接触,屈曲使得管柱与井壁套管因自重或井眼轨迹弯曲所产生的接触力进一步增加,因此单位长度屈曲附加接触力[17]为
(2)
式(2)中:Te为管柱的有效轴向力,N;r为测试管柱与套管之间的环空间隙,m;I为管柱的极惯性矩,m4;E为管柱的弹性模量,GPa。
真实轴向力与有效轴向力的差异源于管柱是否处于含有流体的环境中[23],真实轴向力T用于管柱的强度校核;而有效轴向力Te用于测试管柱弯曲、屈曲判断,是一种不存在的力。
对于井内流体为静流体,真实轴向力与有效轴向力关系可表示为
Te=T+PoAo-PiAi
(3)
若井内流体为动流体则,可表示为
(4)
式中:Po、Pi分别为管柱外压与内压,Pa;Ai、Ao分别为当前管柱内面积、管柱外面积,m2;ρi、ρo分别为管柱的内流体与外流体密度,kg/m3;ui、uo分别为管柱的内流体与外流体流速,m/s。
测试管柱为多级管柱时,除了测试管柱与套管的环空间隙会发生变化,管柱变截面活塞力也不可忽略,活塞力计算公式[24]为
Fpis=(Ai1-Ai2)Pi-(Ao1-Ao2)Po
(5)
式(5)中:Ai1、Ao1、Ai2、Ao2分别为处于单元管柱变截面前端(管柱下端为前,上端为后)管柱内面积、管柱外面积、变截面后的管柱内面积、外面积,m2。
有效轴向压缩力增加至屈曲临界载荷时,管柱将正弦或螺旋屈曲。文献[13-15]研究成果表明,实际的水平井中,不同井段的屈曲构型不相同,不同井段的屈曲临界载荷参考公式如表1所示。

表1 屈曲临界载荷公式参照表Table 1 Buckling critical load formula
1.2 模型求解
封隔器随测试管柱下到预定位置时,测试管柱的受载是测试管柱坐封时轴力的计算基础,因此将下入到预定位置之后的井口载荷Fhook、封隔器处的管柱轴力Fpacker与释放悬重Fslack-off作为已知条件,同时将测试管柱划分为N个单元段,并以井口管柱为起点对管柱单元段从小到大编号。
由于实际井眼轨迹参数存在测量误差,因此需要对井眼轨迹进行平滑处理。常用的处理方法为五点滤波法[25],其表达式为
(6)

由于模型中的轴向力与侧向力存在耦合关系,因此采用迭代法进行计算,整个测试管柱的轴向力计算过程如图3所示。
全管柱的轴向载荷得到确定,则封隔器的实际压重Wp为[26]
Wp=T′packer-Tpacker
(7)
式(7)中:T′packer为释放悬重后的封隔器处管柱轴力,N;Tpacker为未释放悬重时的封隔器处管柱轴力,N。
2 实例计算
针对某深层水平井,使用机械坐封过程的管柱力学分析模型对测试管柱在机械坐封过程中进行受力计算,计算测试管柱轴向力沿井深的分布情况以及封隔器的实际压重,最终确定该井机械坐封施工的最小悬重释放值。其中套管内径为168.3 mm,下入深度8 200 m,实例井及机械封隔器的基本数据如表2~表4所示。

表2 实例井身参数Table 2 Example wellbore parameters

表4 封隔器参数Table 4 Packer parameters of example wells
由于井口悬重释放之后封隔器的实际压重难以测得,只能通过向环空打压验封确定坐封是否成功反推最小坐封悬重释放值。实例井封隔器的最小压重为6.8 t,故采用悬重释放6.8 t为起点,逐渐增加井口悬重释放值,并随后利用向环空反打压(10~11 MPa)验封的方法进行悬重测试,记录封隔器验封合格下井口的最小悬重释放值,最后将本模型所计算结果与现场成功坐封的最小悬重释放值进行比较,若悬重释放值的计算结果大于现场成功的最小坐封悬重释放值,则可验证理论模型的可靠性。
对实例井测试管柱进行受载计算,得到不同释放悬重值下的管柱轴向力如图4所示,经过计算,0与100 kN释放悬重下封隔器处的管柱轴力之差为69.12 kN,即封隔器的实际压重6.912 t,满足封隔器的最小压重6.8 t,故10 t为本模型计算的最小井口释放悬重释放值。
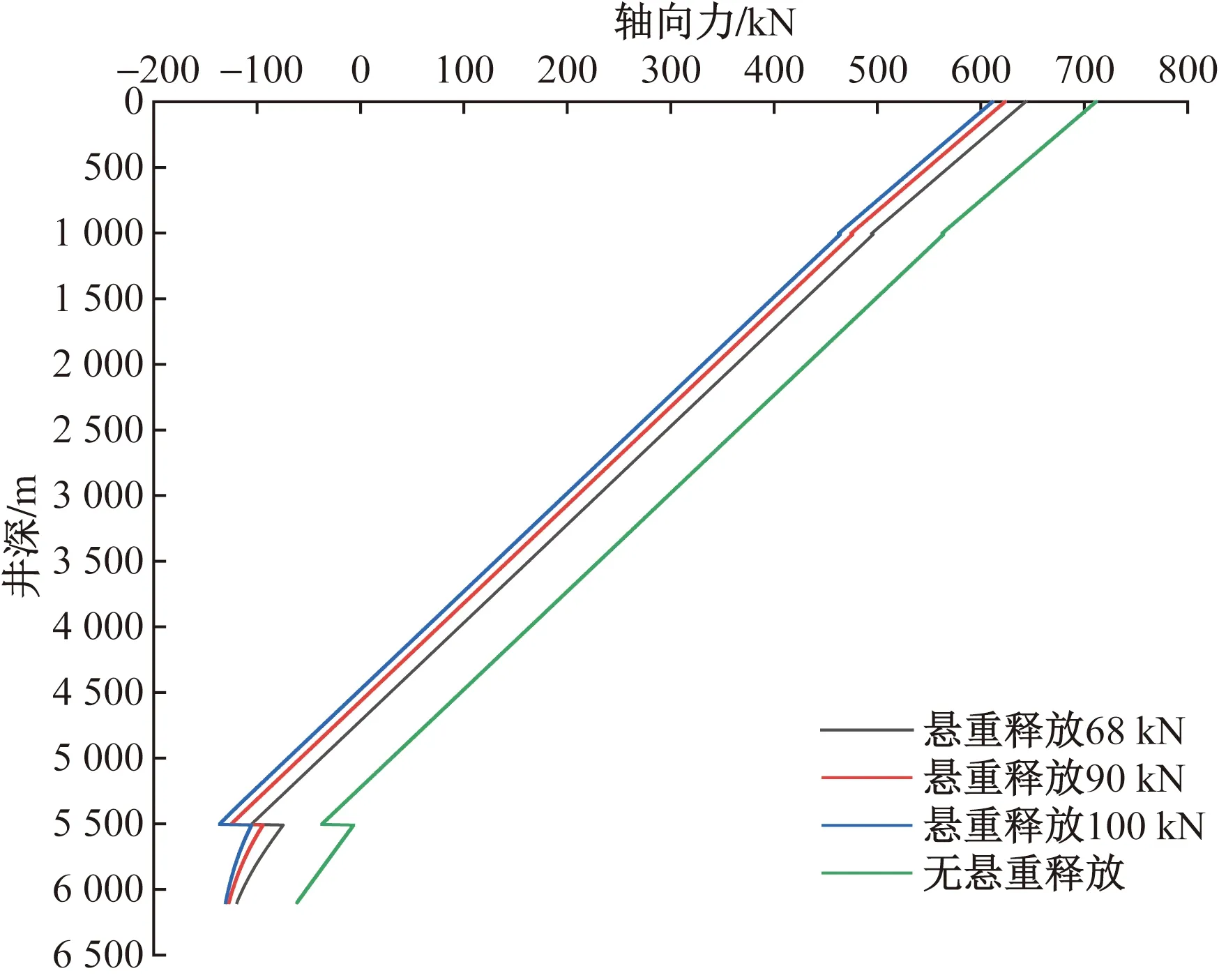
图4 实例井测试管柱轴向受载沿井深分布Fig.4 Axial force distribution of test string along measured depth
现场测试为准确求得坐封合格下的最小释放悬重,以0.5 t增量下放悬重,最终测得测试管柱在8.8 t悬重下井口存在压力变化,在释放悬重达到9.3 t时,井口管柱稳压10 min无压力波动表明验封合格。经过测试得到测试管柱的最小释悬重为9.3 t。理论模型计算数据与现场实测数据对比结果如表5所示。
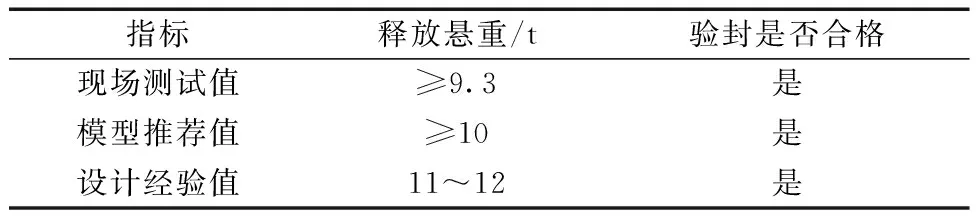
表5 实测数据对比Table 5 Comparison of measured data from example wells
通过现场不断进行验封测试,得到实例井成功坐封时的井口最小释放悬重为9.3 t,而相对于设计经验12~13 t的释放悬重,本文模型计算的最小悬重释放值10 t更接近现场实测,相对误差为7%。因此,本文模型所计算出的结果可对现场释放悬重提供数值支持。
3 敏感性分析
基于本文模型,选用该实例井井况参数,针对井口悬重、油套管环空间隙以及封隔器位置,开展各因素对机械坐封的管柱受力、封隔器压重的影响分析。
3.1 井口释放悬重值对管柱轴向力的影响
由图5可知,无井口释放悬重时,测试管柱轴力沿井深分布呈直线,原因是封隔器位置至井口的井斜角变化很小,井眼轨迹所导致的摩阻小。随着井口悬重的增大,轴力曲线开始出现弯曲,当井口释放悬重达到约400 kN,封隔器处轴力将基本保持稳定。
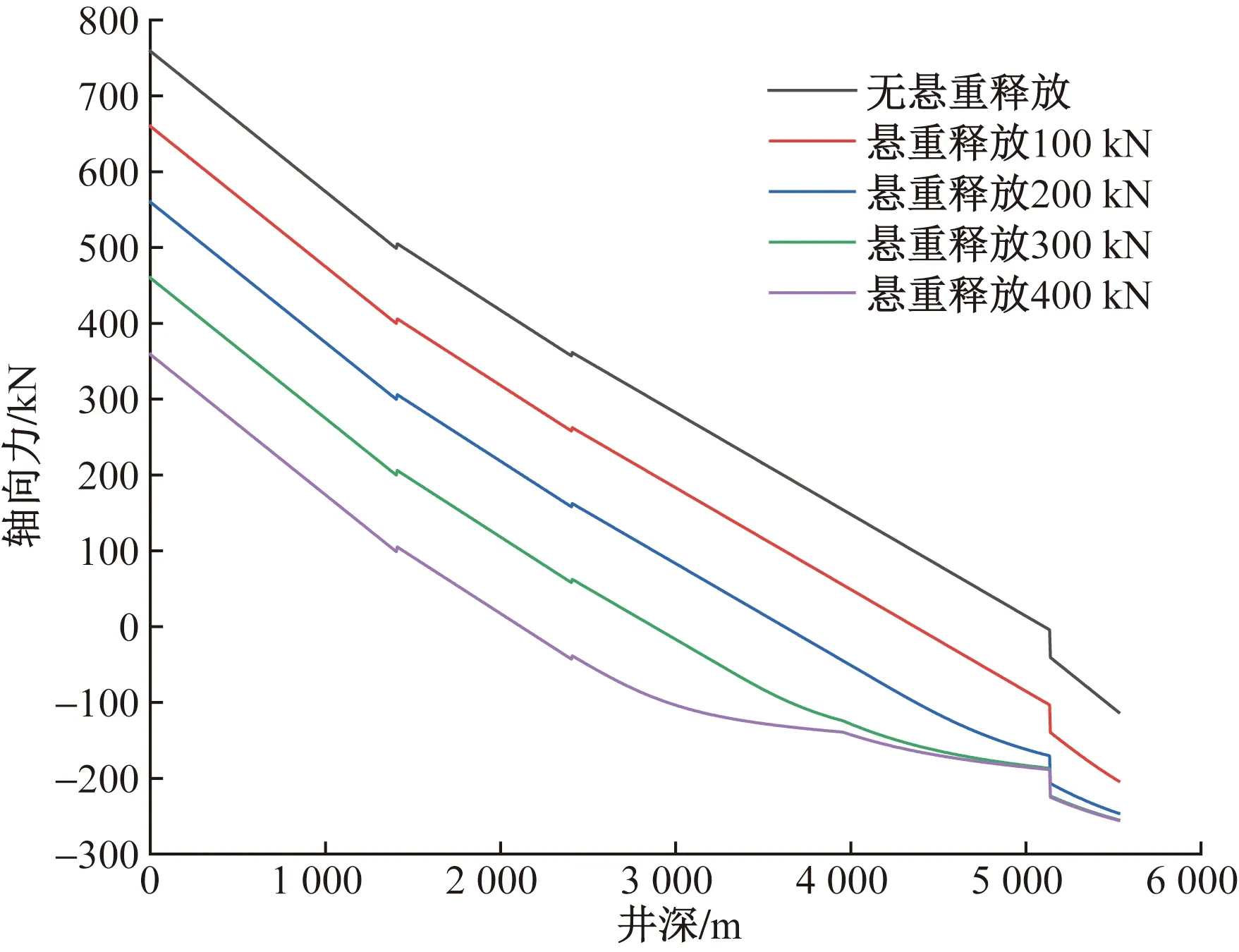
图5 不同释放悬重下管柱轴力沿井深分布Fig.5 Axial force distribution along measured depth under different released slack-off weight
3.2 油套管环空间隙对管柱轴向力的影响
取不同尺寸的中间套管尺寸在同一释放悬重值500 kN进行研究,结果如图6所示。
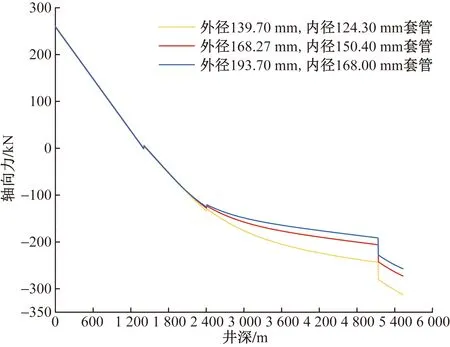
图6 不同套管尺寸下的测试轴向受载Fig.6 Axial force on testing string under different casing sizes
从图6可知,套管内径的增加会使油套环空间隙越大,管柱轴力沿井深的曲线弯曲加剧。表明若测试管柱尺寸不变,管柱屈曲产生的摩阻随套管内径增大而增大,因此采用较小的套管尺寸在一定程度可减缓屈曲摩阻。
3.3 井口释放悬重值对封隔器压重的影响
为研究机械坐封封隔器实际压重与井口释放悬重的关系,通过计算获得机械坐封封隔器实际压重与井口释放悬重关系如图7所示。
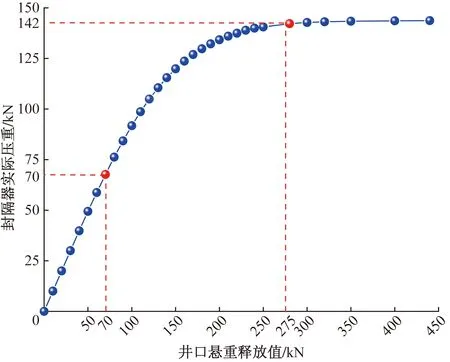
图7 井口释放悬重与封隔器实际压重关系Fig.7 Relationship between the released hook loads from the wellhead and the actual load on the packer
从图7可知,当井口悬重释放值在0~70 kN时,封隔器压重与井口悬重释放基本呈线性关系。当悬重释放在70~275 kN,封隔器压重增长速率随井口释放悬重增大而减缓,管柱屈曲加剧;释放悬重超过275 kN时,封隔器压重将维持在140 kN上下,此时管柱已经处于“锁死”状态,井口释放悬重不再传至封隔器。
3.4 封隔器位置对封隔器压重的影响
为揭示机械封隔器设置位置对封隔器压重影响,将封隔器设置在不同位置,观察井眼轨迹产生的摩阻对坐封效率的影响,同时增加井口悬重释放值观察屈曲对测试管柱坐封的影响。计算结果如图8所示从图8可知,封隔器位置设置在5 000 m以上时,由于测试管柱井斜变化小,100 kN的释放悬重大部分能作用到封隔器上;随着悬重的不断增加导致的屈曲摩阻增加,其坐封效率才逐渐降低。随着封隔器位置逐渐接近水平段及管柱末端,管柱所受井眼轨迹产生的摩阻逐渐累积增大,且摩阻将进一步影响轴力,使管柱受压缩力增大并发生屈曲,管柱坐封效率逐渐降低;随着释放悬重的增加,两种摩阻的叠加将使得坐封效率急剧下降。故进行坐封作业时,若封隔器被设计在水平段,则不宜采用机械坐封。

图8 不同坐封位置与封隔器受力关系Fig.8 Stress relationship between different setting positions and packer
4 结论
(1)针对现场机械坐封井口悬重释放值的选取依赖经验,经验参数易对封隔器造成损伤的问题,提出了一种综合考虑井眼轨迹、管柱屈曲摩阻及变截面影响的测试管柱机械坐封力学分析模型,为机械坐封施工参数设计提供理论支撑。
(2)运用模型对某深层水平井进行悬重释放值设计,模型计算结果与现场所测得最小释放悬重误差为7%,对现场下放悬重提供了数值指导、提高了坐封效率,延长了封隔器的使用寿命。
(3)测试管柱屈曲影响因素主要源于油套管环空间隙和有效轴向压缩力;严重的屈曲将使管柱锁死,使压重不能有效传递;封隔器位置决定了坐封阶段井眼轨迹导致的摩阻力大小,位置越靠近井底,管柱摩阻与屈曲摩阻将进一步增加,最终降低坐封效率。
