基于CNSGA-III算法的乌苏市水资源优化配置

张玉祥, 穆振侠*, 田晓杰

(1.新疆农业大学水利与土木工程学院, 乌鲁木齐 830052; 2.新疆水利工程安全与水灾害防治重点实验室, 乌鲁木齐 830052)

随着社会的进步、经济的发展,水资源的重要性日益凸显。但由于水资源的不合理与低效利用,致使水资源供需失衡,供需矛盾不断加剧[1],为使有限的水资源更好地服务于社会经济发展的需求及满足生态环境保护的需要,水资源优化配置的作用日益彰显。随着水资源配置研究的深入,如何让经济、社会及生态环境3个目标效益都达到相对较优的情况成为当前学者研究的热点与难点。

近年来,针对区域水资源优化配置问题,不同学者从多角度提出了不同的配置方法。朱思峰等[2]以社会、经济、生态效益为目标函数,采用基于分解的多目标进化算法(multiobjective evolutionary algorithm based on decomposition,MOEA/D),明确了侧重经济、社会、生态效益水资源分配方案。方国华等[3]运用粒子群算法探究了区域水量水质联合配置模式。杜丽娟等[4]以公平性最优、缺水率最小为目标,将快速非支配排序遗传算法(non-dominated sorting genetic algorithm-II,NSGA-II)算法用于求解灌区水资源优化配置模型中。李建美等[5]采用基于参考点约束支配的算法(non-dominated sorting genetic algorithm-III,NSGA-III),探究了以区域经济效益最大为目标的的水资源配置方案。在使用优化算法解决多目标水资源配置问题时,不仅要考虑优化算法的收敛性,还要考虑如何选择合适的分配方案,以上研究所运用的智能算法对初值、目标函数要求不高,在处理多变量、多约束的问题上还有所欠缺,同时在方案选择上均以单个目标效益达到最优作为配置方案,这就容易导致所选方案与区域实际情况不符,不能较好满足区域可持续发展的要求。为解决多方案选择的问题,相关方案优选模型相继被提出。单宝英等[6]结合改进的遗传算法与熵权法,进行水资源配置方案的优选。张倪平等[7]运用层次分析法对水资源分配方案进行优选。陆建红等[8]采用逼近理想解排序法(technique for order preference by similarity to ideal solution,TOPSIS),在对各水资源分配方案综合效益评价基础上,进行方案优选。从前期的研究成果来看,关于水资源的优化配置大多数从算法优化的角度出发,研究角度相对单一。其次是关于水资源配置方案的评价方法,目前主要有层次分析法、TOPSIS法、灰色关联法等,这些方法在一定程度上对区域水资源的优化配置具有重要借鉴意义,但也存在一定的局限性[9-10],一是权重的确定主要以专家经验法为主,存在主观片面性;二是评价方法比较单一,难以保证评选结果的准确性[11-12]。

基于此,将熵权-TOPSIS方案优选模型和水资源多目标模型相结合首次运用于乌苏市水资源优化配置研究,并采用优化性能较好的改进NSGA-III算法,简称CNSGA-III算法,研究成果有利于从促进区域社会经济发展、生态环境保护的角度进行水资源的合理配置。

1 水资源配置模型的建立与求解方法

1.1 目标函数

为更好地实现人-水-自然的和谐,达到水资源高效利用的目标,从经济效益、社会效益与生态效益角度进行目标函数的选取,寻求整体效益最佳的水资源配置方案。考虑到的资料的易获取性及对生态环境的敏感性,以化学需氧量(COD)指标作为生态效益目标确定的依据。

(1)根据研究区各用水部门所产生的供水效益总和最大表示经济效益目标,可表示为

(1)

(2)以不同用水部门缺水量总和最小表示社会效益目标,可表示为

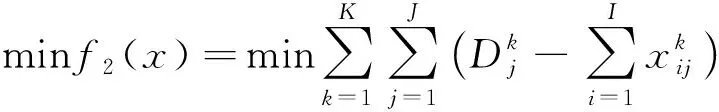
(2)

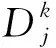
(3)根据研究区各用水部门排放的化学需氧量(COD)总量最小表示生态效益目标,可表示为

(3)

1.2 约束条件

(1)水资源承载力约束。

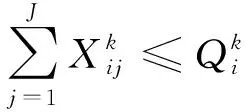
(4)

(2)用户需水量的上下限约束。

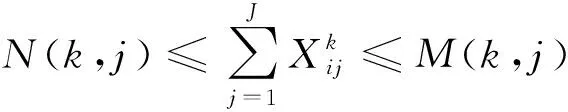
(5)

式(5)中:N为各用水部门需水预测水量;M为需水预测值的1.1倍。

(3)用水总量控制,可表示为

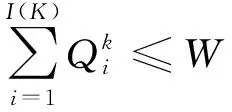
(6)

式(6)中:I(K)为子区K中水源i的数量;W为用水总量控制指标。

(4)变量非负约束。

Xij≥0

(7)

1.3 CNSGA-III算法

考虑到传统优化算法对解决复杂约束条件得局限性,相关学者将Deb约束准则引入NSGA-III算法中,称为CNSGA-III算法,具体步骤如下[13]。

1.3.1 参考点生成机制

为保证种群的多样性,NSGA-III通过目标函数分布的参考点来表示进化过程,通过采用Das and Dennis方法来生成一组均匀分布的参考点集。令参考点集合Q={λ1,λ2,…,λN},参考点满足式(8)。

(8)

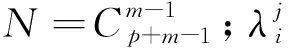
同时为避免随着目标维数变高,参考向量个数加大,出现计算缓慢、时间过长的问题,NSGA-III将采用边界层和内部层的双层参考点机制,分段数为P1、P2。参考点规模可表示为

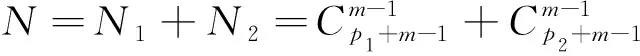
(9)

式(9)中:N1为边界层参考点集;N2为内部层参考点集。

对内部层参考点进行坐标转换,如式(10)最后将参考点集合进行合并,得到完整的参考点集合。

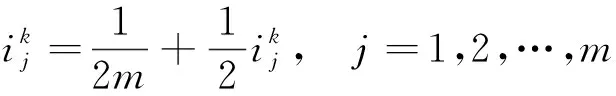
(10)

1.3.2 归一化与环境选择

因为每个函数都有各自的量纲,因此需要进行归一化操作。

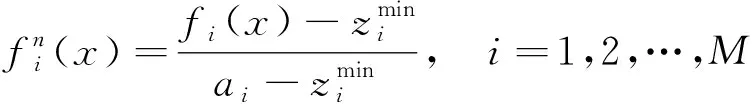
(11)

在环境选择阶段分为3步:①将每个解关联到不同参考点;②将参考点所联系的解的数量称作小生镜数;③选取所有参考点的小生镜数最小的参考点集,并随意选择一个参考点,判断临界层是否有解与其联系,符合条件的解则纳入种群数量,直至种群量达到N。

1.3.3 引入约束条件

选定某个解,判断其是否为可行解,需以约束条件为参考,若满足约束便为可行解,反之为不可行解,为明确不可行解的违反程度,通过约束违反值(CV)[14]来表现,其计算公式为

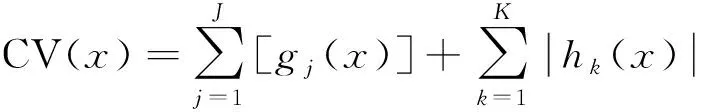
(12)

式(12)中:J为不等式约束数量,对应的gj(x)为不等式;K为等式约束数量,对应hk(x)为等式约束。

当g(x)<0时,gj(x)=-gj(x),否则gj(x)=0。当x满足约束条件中任何条件时,即x在可行域内,CV(x)=0;当x不完全满足约束条件时,即x不在可行域内,则CV(x)≠0。CV值越小,x越靠近可行域。

1.4 基于熵权-TOPSIS综合评价模型的方案优选

为了解决对多指标及多方案评价的问题,考虑到目前使用的TOPSIS法[15]主要依靠专家经验来确定权重,主观性较大,这样会导致最后计算结果明显偏离实际情况,为此以熵权-TOPSIS为方案优选评价模型[16],通过选取贴近实际情况的评价指标,并对其进行标准化处理,客观的赋予权重,最后计算每个评价方案的相对贴近度,从而选择最优的分配方案。有效降低了主观因素的影响,确保评选结果的准确性。

2 实例分析

2.1 研究区概况

乌苏市位于欧亚大陆腹地,准噶尔盆地西南缘的天山北坡经济带区域内,行政隶属于新疆维吾尔自治区塔城地区,地理坐标83°20′E～85°18′E,43°26′N～45°15′N。整体地势自南向北倾斜,呈南高北低、东部略高于西部的变化趋势。乌苏市地处北温带,属典型的大陆性气候,多年平均气温7.5 ℃,多年平均降水量168 mm,多年平均蒸发量为1 164 mm。近年来,随着所在区域开发力度的加大、社会经济的快速发展等,加之灌溉面积的不断增加和各方面用水需求的不断扩大,出现河水超引、地下水超采的问题,河流下游频现断流情况,致使所在区域艾比湖入湖水量锐减及湖面面积萎缩明显;并且伴随着所在区域水资源的不合理开发利用,导致地下水过度开采(超采率达48%),并诱发了其他一系列问题,如超采区及漏斗区频现、生态环境弱化等。因此,从合理开发利用水资源、遏制地下水超采以及脆弱生态环境保护的角度,亟需开展水资源合理、优化配置方面的研究工作。

2.2 规划年供需水预测

以2018年作为基准年,基于用水定额法对规划水平年2025、2035年(来水频率pi=75%)的供需水量进行预测,不同用水行业的用水定额借鉴《城市给水工程规划规范》(GB 50282—2016)、《塔城地区乌苏市农业节水发展规划》及《乌苏市城市总体规划(2018—2035)》,不同水平年各用水部门的需水预测结果如表1所示。将国家最严格水资源管理制度确定的“三条红线”指标中的“用水量控制指标”作为可供水量(表2)。

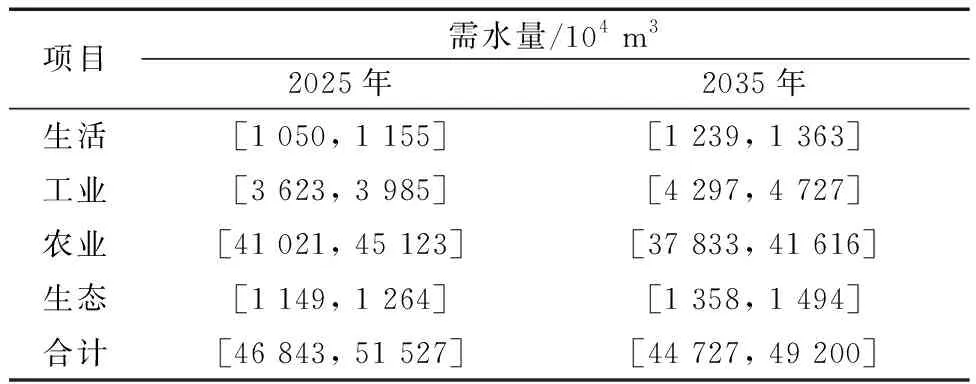
表1 乌苏市规划年需水量预测

表2 乌苏市规划年供水量分析

2.3 模型求解及方案选取

考虑到CNSGA-III算法在求解过程中会产生数量较多的方案集,容易导致决策者在方案选择时陷入困境。为此,首先结合区域发展规划、河流纳污能力以及决策者对各目标函数的偏好程度,来设定各目标效益值的取值区间,缩小方案选取范围,并将满足要求的水资源分配方案作为新的方案集;其次从综合经济、社会、生态效益的角度,建立评价指标体系,以熵权-TOPSIS模型作为方案优选模型,从新的方案集中评选出最优方案,并将其作为水资源优化配置方案。

2.3.1 模型求解

通过CNSGA-III算法对模型求解,得出乌苏市不同水平年水资源配置的Pareto解集合,也称为水资源分配方案集合,如图1所示。图1中的每一个点都由经济效益、总缺水量、COD排放量共同决定,而每一个点就代表着一个分配方案。鉴于本研究对该算法选取的种群规模较大,求解得出的分配方案较多,为了更加精确的选择出合适的方案,在充分考虑当地经济发展、地下水超采情况及现有污水处理设施背景的前提下,选取经济效益在12.0×108～12.2×108元、缺水量在6 600×104～6 662×104m3、COD排放量在144～147 t的15组分配方案作为2025年水资源配置待选方案;选取经济效益在17.1×108～17.21×108元、缺水量在6 273×104～6 284×104m3、COD排放量在135.5～135.7 t的15组分配方案作为2035年水资源配置待选方案。

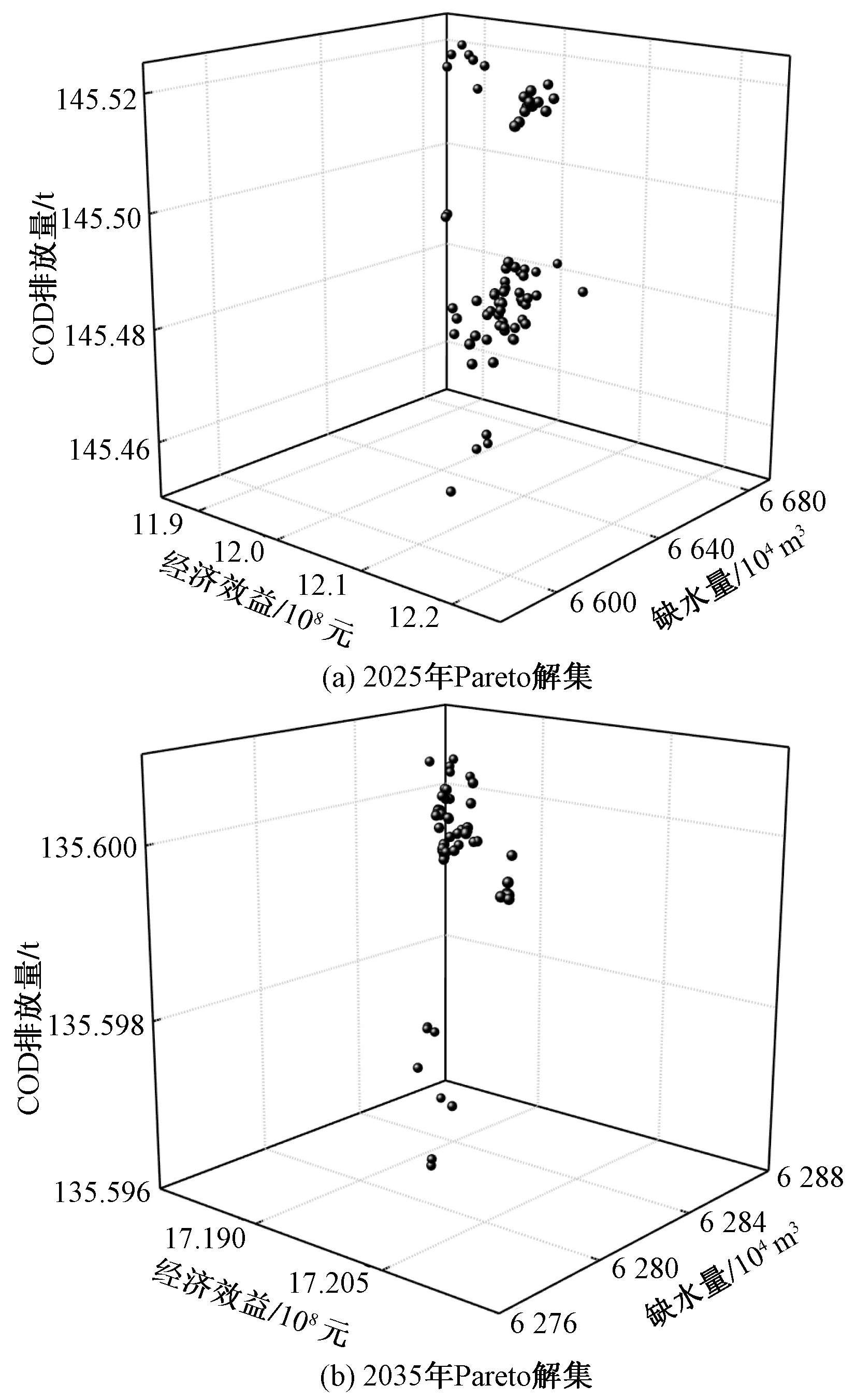
图1 规划年帕累托前沿分布Fig.1 Pareto frontier distribution for the planning year

2.3.2 方案优选

通过对不同水平年15组待选方案对比发现,经济效益最大时,其生态效益最差;生态效益最佳时,其社会效益最差,说明单方面效益最大,并不意味着整体效益最佳。因此以单方面效益最优来考虑水资源利用是不可取的,故需要从综合经济、社会、生态效益的角度来进行水资源优化配置。

为合理的构建评价指标体系,使最终的水资源配置方案更加全面的适合研究的情况,考虑到篇幅限制,仅以2025年为例,基于熵权-TOPSIS模型与15组非劣方案,综合考虑基础资料获取的可靠性与可行性,以经济、社会、生态效益及资源利用为准则层,选用区域缺水率C1(单位:%)、工业供水保证率C2(单位:%)、农业用水比例C3(单位:%)、单方水产出C4(单位:元/m3)、生态供水保证率C5(单位:%)、地下水开采率C6(单位:%)、污水回用量C7(单位:104m3)共7个指标作为指标层(表3),构建方案评价体系,其中指标类型为极小型主要有C1、C3、C6,除此之外均为极大型。具体的指标值及计算出的权重值w如表4所示。由表4可知,在综合评分中方案2得分最高,故选用该方案作为乌苏市水资源优化方案。

表3 水资源配置评价指标体系

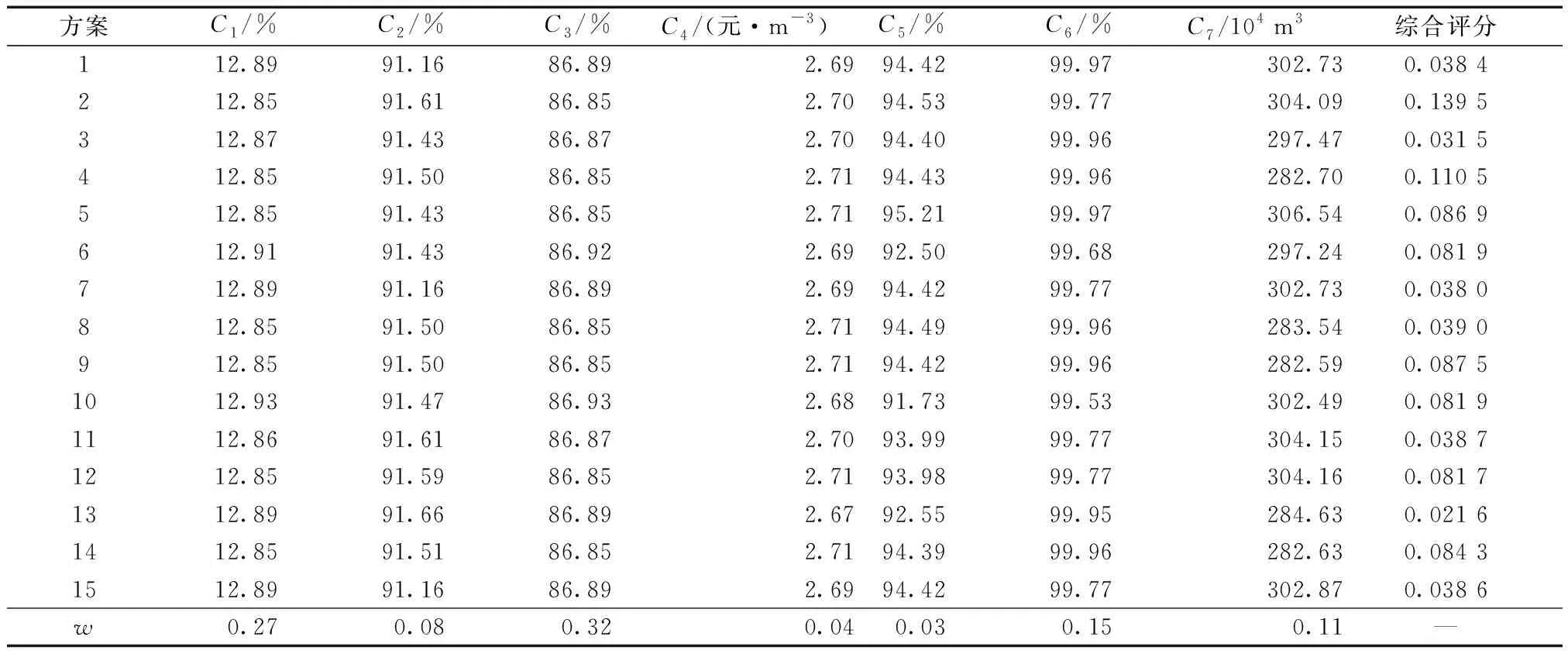
表4 各方案相关指标值

3 水资源优化配置结果分析

3.1 从供需平衡角度分析

从优化后的结果(表5)可以看出,在“三条红线”指标的限额下,配置水量无法完全满足需水,2025年缺水率为12.85%,2035年缺水率为12.77%,其缺水率在不断降低。在规划年中各用水部门均有不同程度的缺水,其中农业缺水率最大,分别为13.57%、13.48%。所在区域现状年用水量已经超出“三条红线”指标限额的20%,并且农业用水占比达到95%,存在较突出的压减用水量的任务;规划水平年能用的红线指标更少,而水的需求日益上升,因此在该形势下缺水是无法避免的,鉴于农业用水占比较大及其保证率较其他用水部门低,因此农业缺水的问题更加突出,这就要求所在区域严格执行非法耕地退减、大力发展高效节水与退耕还林还草等措施的严格实施,其他各业也应该加强节水用水,以缓解水资源不足的突出问题。

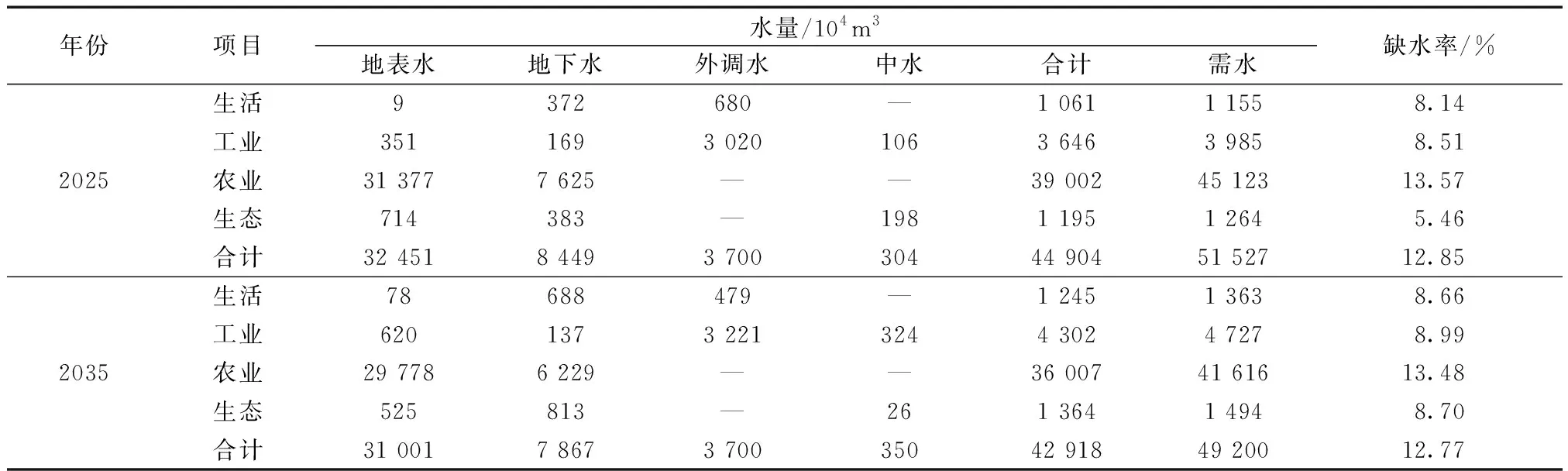
表5 2025年、2035年水资源优化配置结果

3.2 从用水结构比例分析

从用水结构比例分析可以发现,2025年生活、工业、农业、生态用水比例为2∶8∶87∶3;2035年为3∶10∶83∶4,与现状年用水比例(2∶3∶93∶2)相比,农业用水占比分别下降6%、10%,工业用水占比分别了提高5%、7%,表明通过水资源潜力挖掘、节-减水措施的实施、水资源的优化配置等,在一定程度能够使当地水资源更合理地加以利用,并使之朝有利用于经济发展与生态保护的方向过渡。优化后的用水结构能有效缓解当地由于农业用水占较大而诱发的用水矛盾突出的问题;同时工业、生态用水比例的提高,能够极大促进当地的经济发展、生态环境的持续改善,有助于逐步实现人-水-自然的和谐发展。

总体来看水资源优化配置方案及配置结果符合乌苏市的实际发展状况,具有一定的实践意义及参考价值。

通过对不同水平年配置水量对比(表6)可知,2025年、2035年优化后的供水量较原始供水量均有递减趋势,其节水总量分别为50×104m3、9×104m3。与现状年单一的地表水、地下水供水结构(53∶47)相比,规划年供水水源结构发生了改变,更加趋于合理,其中地表水、地下水、外调水、中水供水比例为72∶19∶8∶1,地下水占比下降28%,在一定程度上能有效遏制地下水的超采。

表6 不同水平年水量对比结果

通过优化后的规划年目标效益值(表7)可以看出,在经济不断提高的同时,其缺水率及COD排放量也在逐步下降,配置较为合理结果,验证了CNSGA-III算法的适用性。

表7 乌苏市水资源优化配置效益值

4 结论

以社会、经济及生态效益函数为目标,建立CNSGA-III算法及熵权-topsis模型的水资源优化配置模型,通过对比优化前后的水资源配置结果,充分说明了该算法在研究区的可行性及适用性,为不同行业的用水提供合理化建议,得出如下主要结论。

(1)构建的乌苏市水资源优化配置模型,引入了CNSGA-III算法进行求解,避免了收敛性不足、容易陷入局部最优等问题,求得了乌苏市2025年、2035年水资源分配方案非劣解集合,并根据当地的经济发展要求及现有污水处理设施的背景条件,考虑一定范围内的经济、社会及生态效益作为参考来选择合适的方案,最后选出15组非劣方案

(2)为了更加全面的选择适合乌苏市的水资源分配方案,引入熵权-TOPSIS评价模型,对15组非劣方案进行优选,在合理考虑各个目标效益的前提下,通过判断每个指标所含信息量的多少,客观、公正的,选出合适的方案。

(3)优化后的配置水量较原始供水量有递减趋势;2025年、2035年优化后的工业用水结构比例相比于现状年提高5%、7%,农业用水占比下降6%、10%,能有效缓解当地由于农业用水占比较大导致用水矛盾突出的问题,优化后的水源结构相比于现状年更加合理,地下水占比大幅度降低,有效遏制了地下水超采。表明水资源优化配置后的合理性及可行性。

在规划年需水预测上采用的是传统的用水定额法,以人口,灌溉面积,工业增加值为主要因素来进行需水计算,计算过程简单方便,但在实际中影响需水量的因素有很多,需进行系统的分析来确定出主要的影响因素,这样计算结果才会更加准确,在进行模型求解时,通过借鉴文献[17]的CNSGA-III算法来求解模型,解决单一算法时存在的算法性能缺陷问题,在方案优选上,传统的方案主要有:经济效益最大、社会效益最大、生态效益最大,但这些方案都过于片面,无论哪一个方案都只侧重于一个方面,而所采用的熵权-TOPSIS优选模型能较好地结合当地的发展情况,并综合3个目标的效益值,选择出适合的发展方案,如果条件允许,应尽可能多地选取能够反映当地实际情况的指标,更好地完善方案优选模型。在配置结果上,优化后的结果与优化前的结果相比,效果明显,对比前人对水资源优化配置后的研究成果来看,在用水结构,供水结构,以及用水总量上,变化趋势基本一致,符合配置要求。