数据子空间提取方法研究及应用

司立娜, 颜志强, 刘祖耀, 刘路, 朱亮

(1.深圳长城开发科技股份有限公司, 广东, 深圳 518035;2.西安电子科技大学, 机电工程学院, 陕西, 西安 710000)

0 引言

工业数据本身具有规模大、数据产生更新速度快、类型多而杂、价值密度低的特征,电子产品生产制造过程中也是如此,并且产品的过站工序合格率通常可达99%,异常的数据少,因为异常数据往往只会偶发于某个工序或某台机器设备或某一段未知的短暂时间段内,这就使得所产生的数据大多数为合格数据,异常数据占比非常小,这种不平衡状态分布的数据容易使得异常数据中的价值信息被掩藏,为进一步识别工艺参数改善因子,需要考虑如何从这种不平衡数据中提取出有价值的数据子空间进行研究。

数据子空间是相对于数据全空间而言,在刻画数据的所有特征属性中提取少量关键属性来组成新的数据空间,尤其是对高维的不平衡数据进行分析时,显得尤为重要。文献[1]使用PSO-SPLOF算法来探讨研究局部离群数据的子空间划分,文献[2]给出了使用信息增益的决策树算法应用到网络高维软子空间聚类中,文献[3]给出了一种基于基尼指标加权的离群子空间数据挖掘方法,文献[4]为解决实际财务数据分布的不平衡性,提出了将马田系统与集成分类算法(AdaBoost)相结合的算法设计,此算法可实现自动调节分类器样本的概率来更正平衡度。这些方法的应用也表明了数据挖掘的方法在提取和挖掘处理数据子空间及数据平衡分布中发挥着重要的作用,所以对于实际应用的工业数据,提出了基于传统CART树和CART树改进方法研究提取数据子空间。

1 研究方法与应用

传统的机器学习方法在具有超低价值率的工业数据挖掘中发挥着重要作用,如何从大量无规律的、超低价值率的数据空间中提取出具有明显规律特征的子空间数据集是本文的主要研究出发点,基于实际应用案例的需求,探索使用数据挖掘算法,包括传统的机器学习算法(CART)和改进的算法(双CART)来进行研究。

1.1 分类回归树(CART)

分类回归树(CART)算法最早由BREIMAN等[5]提出,目前已在统计领域和数据挖掘技术中普遍使用。它是用基尼系数代替熵模型,将最大化不纯度降低(或等价地,具有最小基尼指数)的属性选择为分裂属性,由CART算法构建的决策树在很多情况下比常用的统计方式构建的代数预测更加准确,而且数据越复杂,变量越多,算法的优越性越显著。

CART算法又称CART决策树算法,是应用于分类的一种树结构,其中每个内部节点代表某一属性的一次测试,每条边代表一个测试结果,叶子节点代表某个类或类的分布。CART算法基于基尼指标求出作为根节点的属性,然后自上而下以递归的方法构建模型,直至每个样本集在划分后都是完全纯净的,则停止建树。基尼指标用于度量样本的杂质度,对于样本集合D,定义[6]如式(1)

(1)

基尼指数考虑每个属性的二元划分,当考虑二元划分裂时,计算每个结果分区的不纯度的加权和,如果A的二元划分将D划分成D1和D2,则给定该划分,D的基尼指数为

(2)

1.2 分类回归树的改进(双CART)

在实际应用的工业数据中,传统的CART算法主要表现为分类准确率偏低,算法计算量偏大等情况,所以对传统CART方法进行改进,即提出了双CART法,增加人工设定阈值的方向进行后剪枝和两次CART分类树创建,目的是减小计算量,使得分类更加精确。双CART具体算法步骤如下:

Step 1 对所选原始超限数据构建第一棵CART树,得到叶子数据集{s1,s2,…,sn},每个叶子中均包含正负样本两类(即超上限类和超下限类);

Step 2 设定样本量初始阈值N0(一般选取总样本量的10%)和正负样本比例值初始阈值R0(一般初始选择60%,对第一步所产生的叶子数据集进行筛选,得到满足条件的候选数据子集{h1,h2,…,hk};

Step 3 对第二步所筛选得到的候选数据子集继续构建CART树,得到k棵CART分类树,计算每棵分类树的AUC,并设定AUC阈值,选择出最优分类路径和此路径的叶子数据集的样本量N及R;

Step 4 根据新的样本量N及R定为最终设定样本量和正负样本比例值阈值选取,返回Step 2继续,得到最终最优分类路径和最优数据子空间。

1.3 实例应用

机加工关键尺寸是公司产品生产工序中最重要的质量控制参数,将双CART分析方法应用到了尺寸数据分析当中,进一步筛选出尺寸异常数据的影响因子,指导生产现场工艺参数优化,目的是提高产品生产工艺能力指数,满足客户需求目标。

机加工关键尺寸数据的相关影响因子有机台号、停机时间、车间温度与测试温度之差(又称温度差)、抽检时间与测试时间之差(又称时间差)、真空值等。使用双CART方法,在第一步CART分类时设定初始阈值候选数据集数据量为最小30,叶子节点的正负样本比例最小60%,筛选出风险路径为超下限候选数据集路径5、路径7、路径10,超上限候选数据集路径1、路径4、路径6、路径9、路径13。继续对这些路径的叶子数据进行第CART分类,选择分类准确性AUC大于0.9的路径为最优分类路径,即风险最大路径,迭代优化得出选择候选数据集时设定样本量阈值N最小为50,R最小为70%,同步得到最优分类路径为机台号、待机时间、机台号,路径分析发现主要影响因子集中于机台号(2,9,16,22,23,37,41,46)和停机时间(小于2426 s内,即停机重启后2426 s内),这些是需要重点关注和改善的方面。双CART方法有效提取到了异常数据的属性子空间,同时也减少了传统CART算法的冗余计算量,并识别到了机加工关键尺寸数据的主要影响因子和改善方向。

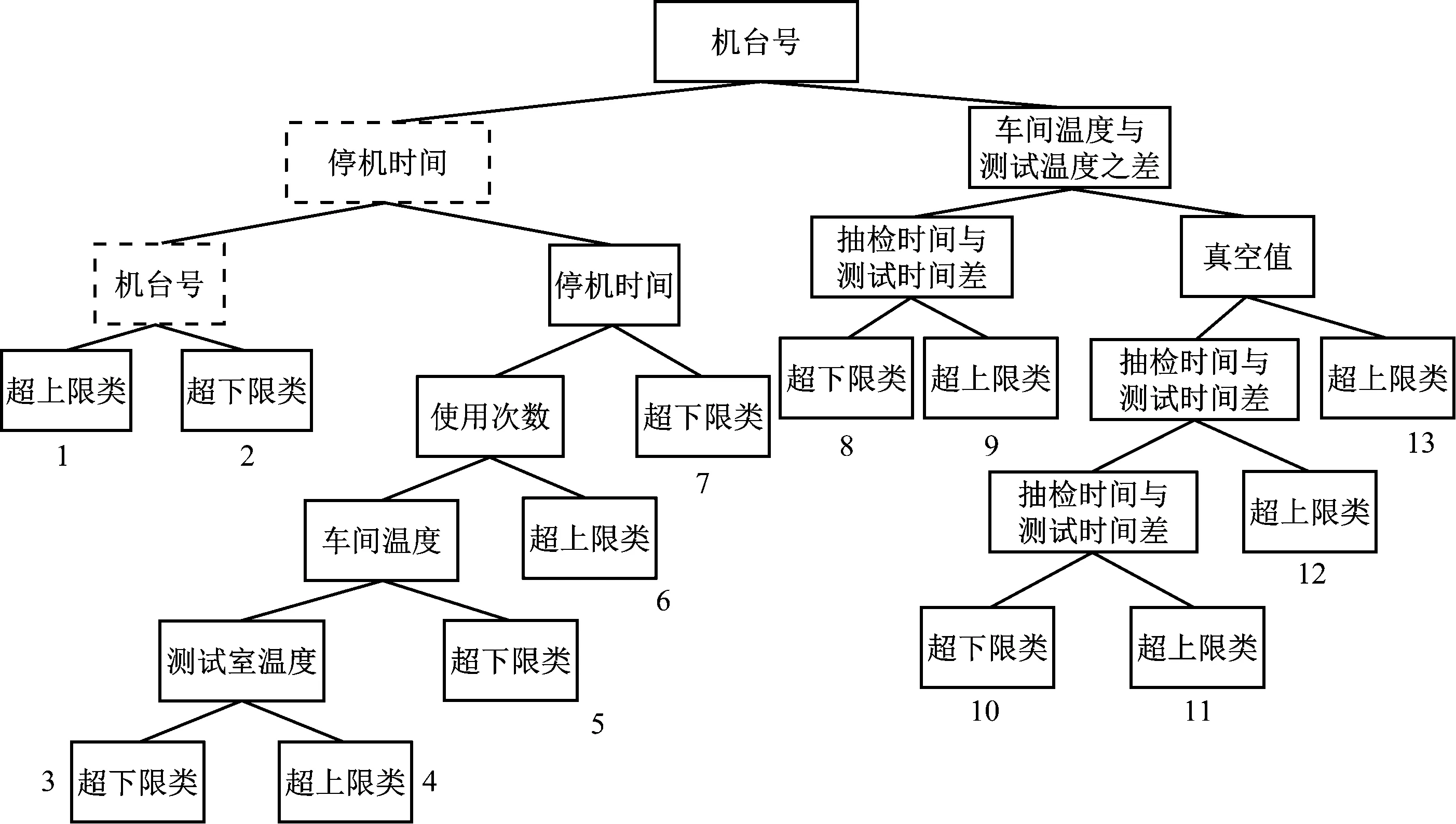
图1 CART树输出结果

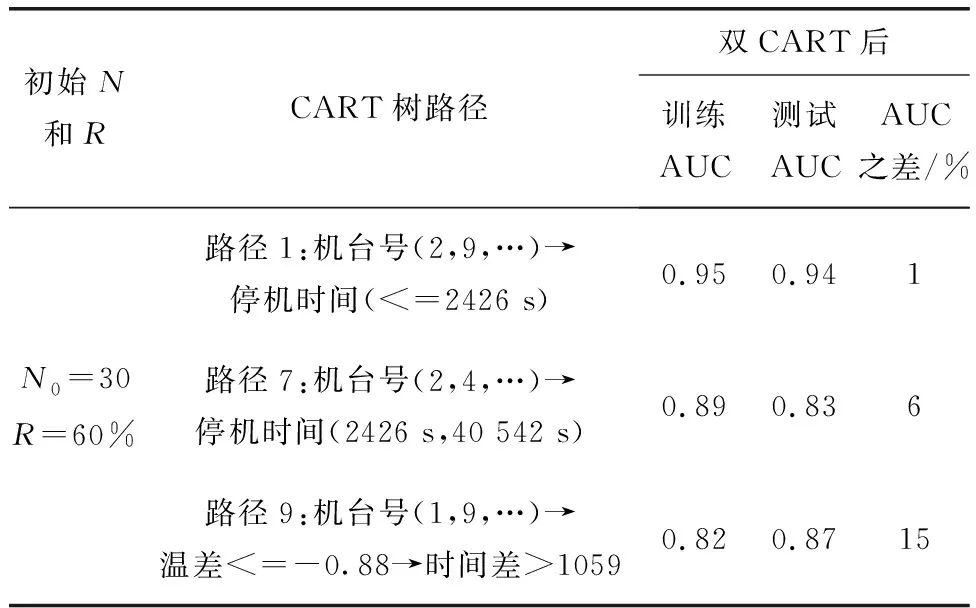
表1 双CART输出路径(初始N0和R0)部分示意表

表2 双CART输出最优路径结果(AUC阈值>0.9)

2 总结

本文提出了使用双CART方法进行数据子空间提取处理分析,并应用到机加工关键尺寸数据分析,实例表明双CART方法应用分类效果显著,可以从大量无规则的数据中提取有强相关的数据子空间,并且使用双CART方法识别到了影响尺寸质量的主要属性因子及风险路径,明确了机加工设备长时间停机重启后的重点监控时段时长,给出了在此时段内需要进行特殊监控的建议,即现场工艺人员重点关注此时段产出质量并持续调整机加工设备关键参数,结果验证了改善措施实施后工艺能力指数得到了提升。