定常线性薛定谔方程的一种高精度数值解法

张红梅，尹江华

（1.湖南工业大学 理学院，湖南 株洲 412007；2.株洲欧科亿数控精密刀具股份有限公司，湖南 株洲 412008）

1 研究背景

薛定谔方程是量子力学的基本方程之一，其地位与牛顿方程在经典力学中的地位相当。薛定谔方程已被广泛应用于理论物理、核物理、等离子物理、电磁波理论、化学、光学工程、地震学等领域之中。但对于这些实际应用中的大量复杂问题，用经典的解析方法和实验研究方法大多难以求解。随着计算机技术的快速发展，数值解法已成为其另一重要且有效的求解方法。薛定谔方程是耦合方程组，它还涉及复函数，采用经典的离散方法在单层网格下离散原方程所得的离散系统，通常规模较大，耗费大量的计算时间。因此，构建快速的数值解法十分必要。

有限体积元算法除了处理边界灵活、计算简便外，还能够在一定程度上保持物理量的局部和全局守恒性。这些性质使得有限体积元算法成为一种重要方法。近年来，学者们分别采用不同的有限体积元算法求解椭圆方程[1]、Navier-Stokes 方程[2]、扩散方程[3]等。

在求非对称问题或非正定问题的有限元解时，提出了两网格离散算法[4]，并将该算法应用到求解非线性边值问题[5]、Navier-Stokes 问题[6]、流体问题[7]等。随后，两网格有限元算法又被成功地应用于求解耦合方程组[8]，并进行了一系列的推广与应用[9-12]。在上述研究的基础上，C.S.Chien 等[13]采用两网格差分法求解非线性薛定谔方程组；Wu L.[5]用两网格混合有限元算法求解非线性薛定谔方程组。

近年来，国内外许多学者将两网格离散思想与有限体积元算法相结合，用于求解椭圆方程定解问题[14]、非线性双曲方程定解问题[15]、抛物方程定解问题[16]等。本文将有限体积元算法计算的灵活性与两网格算法的快速性相结合，构建两网格有限体积元算法，用于求解耦合方程组——定常线性薛定谔方程边值问题：

λΔ 为动能算子，且λ为正实数；

u(x)、V(x)、f(x)分别为未知函数、位势函数、右端项，均为复函数。

在实际计算时要将解的实部与虚部分开成如下等价的耦合方程组：

式中：u1(x)、u2(x)分别为u(x)的实部和虚部函数；

V1(x)、V2(x)分别为V(x)的实部和虚部函数；

f1(x)、f2(x)分别为f(x)的实部和虚部函数。

为了方便，假设

2 线性有限体积元算法及误差估计

方程（2）的变分形式可描述为：

设Th={ei}、Zh分别是形状正则的三角形网格剖分所有单元和剖分点的集合[9]，h为剖分步长。定义线性有限元空间

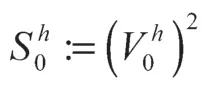
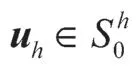
由式（4）和（8）可得正交关系

并在条件（3）成立的情况下，问题（8）的有限元解uh满足

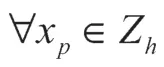
由文献[1]可知算子Ih满足引理1。

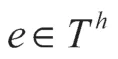
为简化方程组（2）的计算，将方程组（2）的前两式在控制体bp上积分，并利用 Green 公式可得

式中n为控制体边界的单位外法向量。

对上两式等号左边第二项进行近似计算，即控制体bp上的积分，被积分函数ui(x)取近似值ui(bp),i=1,2，进行计算，得，将上面两个方程两边分别乘以Ihw1和Ihw2，并对bp求和，则有

为了对式（13）和（14）化简，先给出如下引理2[2]。

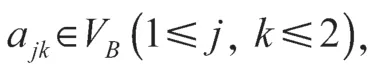
利用引理2 可得

由直接验证可知

将式（15） 和（16） 代入式（13）和（14），可得如下线性有限体积元变分问题：

定义范数容易证得

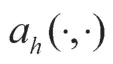
由引理3 和Lax-Milgram 定理知，变分问题（17）的解存在且唯一。

根据文献[9]有引理4。

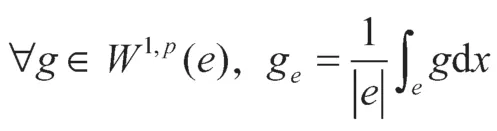
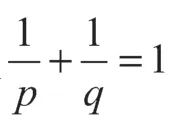
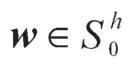
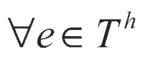
引理5 证毕。

根据文献[2]中的式（3.10）有

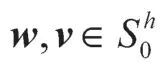
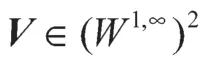
利用上式和式（23）可得式（24）。引理6 证毕。

引理7设u、uh分别为方程（2）和（17）的解，则有

证由式（21）、（17）和（19）得

引理7 证毕。

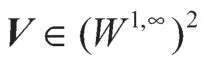
因而有

证由式（8）和（17）有

当式（22）和（24）中p=q=2 时，再联合式（25）则有

在式（26）中，令v=uh-uh，再由式（9）可得式（27）。引理8 证毕。

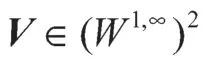
证由式（7）、（10）和（27）得

定理1 证毕。

3 两网格有限体积元算法及误差估计

为了简化式（18），将其拆成两部分并引入记号：

两网格有限体积元算法：

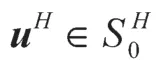
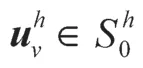
因而有

证将式（17）减去式（29），再由式（18）得

由假设条件（3）及式（12）、（19）、（25）和（28）可得

即得式（31）。

再由式（28）和（31）得

定理2 证毕。

4 两网格有限体积元算法数值实验

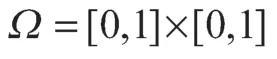
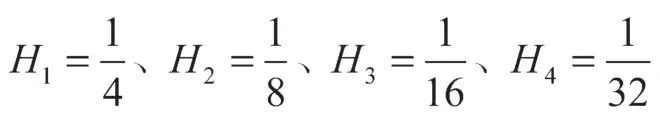
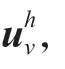
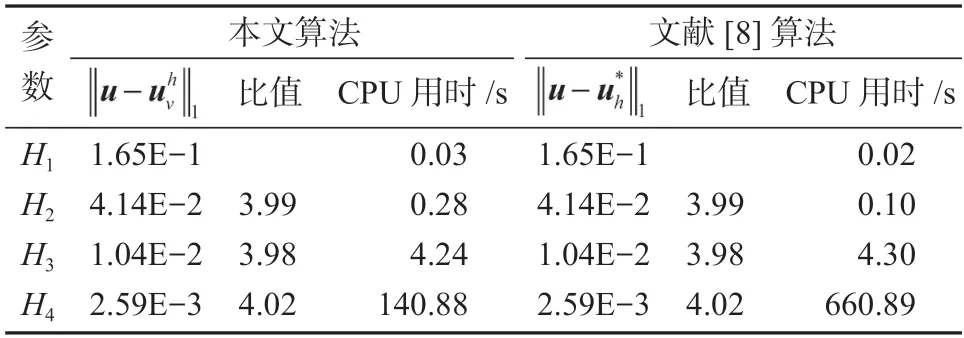
表1 λ=1 时两种算法的结果比较Table 1 Comparison of results between the two algorithms with λ=1

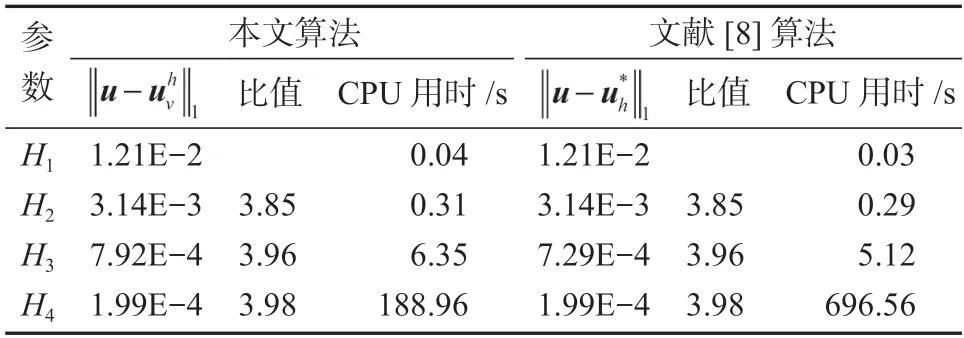
表2 λ=100 时两种算法的结果比较Table 2 Comparison of results between the two algorithms with λ=100

5 结语

薛定谔方程的实际应用比较广泛，方程的离散系统规模庞大。本文在已求出定常线性薛定谔方程两网格有限元解的基础上，重新构造了薛定谔方程的一种新的快速数值解法——两网格有限体积元算法。从理论上证明了该算法达到最优收敛阶，并用数值实验验证了该算法能节省大量的计算时间，极大地提高了求解效率。