能耗约束下基于预算等级的调度长度最小化算法

刘丹彤，张龙信，杨 佳，暴子豪，艾明慧

（湖南工业大学 计算机学院，湖南 株洲 412007）

1 研究背景

异构云系统（heterogeneous cloud system，HCS）由多个计算单元连接组成，其可扩展性强，在分析处理海量数据和进行大规模科学计算时发挥着重要作用[1-2]。随着人工智能、大数据和云计算等技术的飞速发展，计算的应用需求和系统性能都趋向多样化和复杂化，系统架构集成度不断提高，导致计算功耗显著增加，产生了更高昂的电力成本，甚至对环境造成了污染[3]。降低计算系统的能耗已成为当前HCS 开发和使用所面临的主要瓶颈，也是影响经济和生态技术发展的重要因素。推进节能能够提高计算设备的利用率，促进经济可持续发展[4]。

近年来，在能耗约束下进行科学工作流调度已经引起了广泛的研究。在电压和频率可变的虚拟机（virtual machine，VM）上进行能耗感知任务调度一直被学者们广泛研究[5]。动态电压和频率缩放（dynamic voltage and frequency scaling，DVFS） 作为一种被广泛使用的降低系统能源消耗的经典技术，主要通过调整VM 上的电源电压和频率来进行功率感知任务调度，提高能量效率比，从而实现对系统能耗的控制[6-7]。

HCS 中基于功率感知的任务调度长度最小化一直是一个研究热点。Tang Z.等[8]提出了利用空闲时间的回收来合并效率较低的VM 以实现对空闲时间的有效利用，减少能量浪费。Song J.等[9]提出了一种有效的调度算法，在能耗受限的情况下，通过对松弛能量的相对平均分配以最小化应用程序的调度长度。王兰等[10]将节点根据其通信开销和计算开销划分为单独的队列，再将关键节点划分到适合的队列中，减少了工作流的完工时间并提高了处理器的调度效率。Li K.Q.[11]将关注重点放在静态功耗上，通过解析方法建立了具有给定能耗约束的并行任务集的最小调度长度，同时建立了给定调度长度约束下任务集最小能耗的下界。该解析思想为具有动态和静态功耗工作流调度提供了分析方法，以评估启发式算法性能。A.K.Maurya 等[12]在基于能量感知服务的水平协议和不改变最大完工时间的前提下降低频率，同时利用预测最早完成时间算法以计算工作流的完工时间。文献[13]提出了两种经典的算法，其中异构的最早完成时间优先算法（heterogeneous earliest-finish-time，HEFT）是一种基于插入思想的最小完成时间算法，而关键任务置于同一处理器算法（critical-path-on-a-processor，CPOP）则在任务优先级阶段进行了改进，并最小化关键任务的执行时间。M.Sulaiman 等[14]将启发式算法和元启发式算法的思想相结合，利用列表和任务复制思想提出了两种基于遗传算法的任务调度算法，能够实现较低的复杂度前提下优化调度长度和平均调度长度比等多项指标。

近年来，Xiao X.R.等[15]在异构系统上探究了能耗约束条件下并行应用的调度长度最小化问题，并提出了能耗约束下最小化调度长度（minimum schedule length with energy consumption constraint，MSLECC）算法。其主要思想是将工作流的总能耗约束传递给每个任务，从而使得调度过程中的关注点转移到每个任务，然后以启发式的调度方法最小化工作流的调度长度。MSLECC 算法具有良好的性能，但MSLECC 算法在能耗预分配阶段直接为每个未调度任务分配了其最小能耗，这种预分配方法虽能满足总能耗约束条件，但公平性欠佳，任务集的调度长度并不乐观。因此，需要设计一种高效的调度算法以减少调度长度。

基于此，本文提出预算等级（budget level，BL）分配机制这一全新的概念，将应用程序的能耗约束合理地传递给每个任务。BL 分配机制不再使用最小能量预分配方法分配任务的能耗约束，而是根据任务自身能耗水平作为一种智能权重分摊能耗，避免因任务优先级敏感而使能耗分配不公。本文基于这一分配策略提出了能耗约束下最小化调度长度算法（minimizing scheduling length under energy constraints based on budget level，BLMSL），能在能耗约束条件下取得较小的调度长度，减少任务优先级对能耗分配的影响。

2 基本模型

2.1 应用模型

本文应用的一个典型工作流图如图1所示。

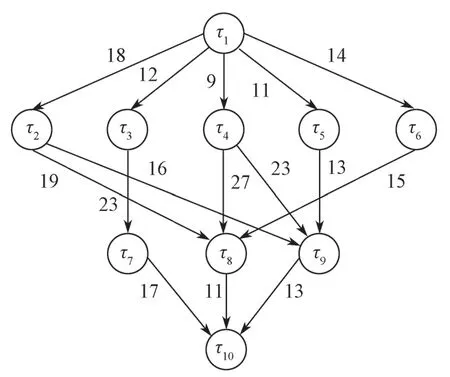
图1 一个典型的工作流图Fig.1 A typical workflow diagram

本文的目标计算平台由一组计算、存储能力各异的VM组成，VM资源池用VM={vm1,vm2,…,vm|VM|}表示，其中|VM|为虚拟机的数量。并行应用任务集（directed acyclic graph，DAG）通常使用有向无循环图G=(N,E,C,W)表示，其中N为G中任务τi集合，即τi∈N。E表示G中直接相连两任务节点的通信边集合，每条边ei,j∈E表示连接任务τi和任务τj的通信边。C为直接相连两节点间通信边的时间开销集合。若τi和τj分配给不同VM，ci,j为τi和τj间的通信时间。W为任务在不同VM上执行的通信成本集合的矩阵，wi,k表示任务τi分配在vmk上执行时所需的计算开销。

对于G中任意直接相连的两个任务节点τi和τj，ei,j∈E表示只有当任务τi执行完毕，并且任务τj执行所依赖的所有数据准备就绪，τj才可被执行。在给定的DAG 中，没有前置任务的任务为入口节点，记做τentry；没有后续任务的任务为出口节点，记做τexit。表1 显示图1所示DAG 中各任务在不同VM上的计算开销。

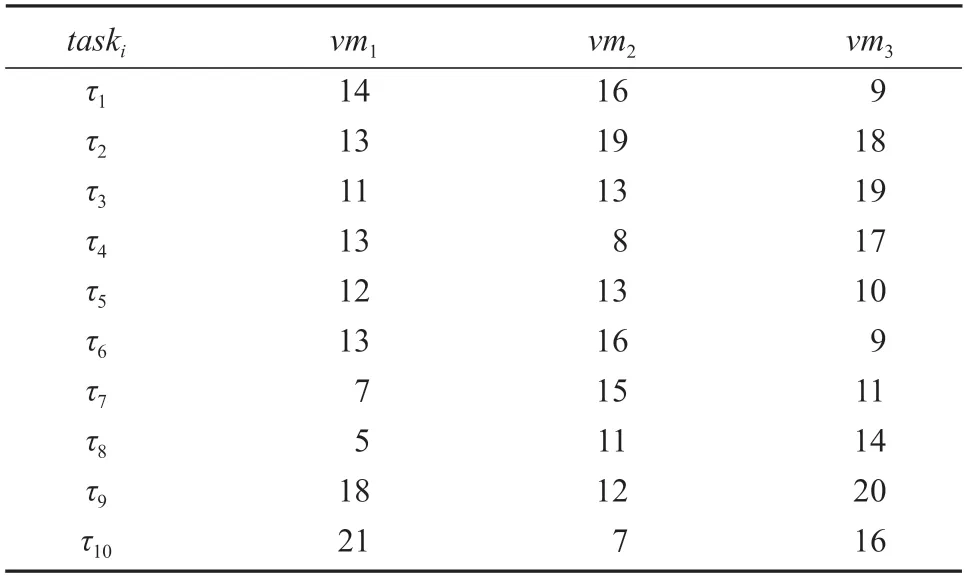
表1 任务的计算开销Table 1 Task calculation cost

2.2 功率和能耗模型

DVFS 基于电源电压与工作频率的线性关系，依靠降低频率减小电源电压，达到节能的目的。本文假设一个支持DVFS 的系统，采用广泛使用的系统级功率模型为HCS 建模，能耗表达式为

式中：φs为静态功率，其主要包括维持电路工作的基本消耗及存储器休眠状态时的能量开销，系统在打开或关闭时，相关的开销较大，使得φs始终处于消耗状态；φind+φd表示动态功率，其中φind为与频率无关的动态功率，只有通过关闭整个系统的电源才能消除；h为系统状态，指示当前系统是否消耗动态功率（系统处于激活状态时，h=1；系统处于关闭状态时，h=0）；φd为系统动态能量消耗，为与频率相关的动态功耗，通常表示为

式中：Ceff为有效负载电容；Vdd为供应电压；为时钟频率。

当系统以较小的频率运行时，由于φind的存在，系统总能耗的减少并不明显，因此存在最低节能频率，其表达式为

由于系统中VM的异构性，本文定义以下集合：与频率相关的动态功率φd集合，

与频率无关的动态功率φind集合，

有效电容Ceff的集合，

实际有效频率的集合，

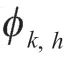
其中，

3 BLMSL 算法

3.1 相关知识

为了便于理解，本文进行如下定义。

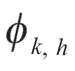
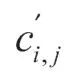
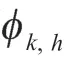
定义3调度长度（SL）是并行应用集从入口任务开始执行，到出口任务执行完毕所花费的总时间，即出口任务的实际完成时间与入口任务的实际开始时间的差值，可表示为

式中AST(τentry)为入口任务的实际开始时间。

3.2 问题描述

本文所研究的问题是在满足用户能耗约束的条件下，针对用户提交的工作流任务图，以最少的时间完成调度，提高用户服务质量。即在不超过能耗约束的条件下，为每个任务分配具有适当频率的可用VM，同时使得DAG 应用程序的调度长度最小。

能耗约束下并行应用的调度长度最小化问题可以形式化表示如下：

式中：E(G)为工作流所消耗的实际能量；Ebdgt(G)为工作流的预算能耗约束。

由于工作流总能量是所有任务能量之和，工作流的最小能量值Emin(G)和最大能量值Emax(G)可表示为

任务τi的最小能耗Emin(τi)和最大能耗Emax(τi)分别以最小和最大频率遍历所有的VM获得，其表达式如下：

3.3 任务优先级

在将任务分配给VM之前，首先需要确定任务调度的顺序。

定义4向上优先等级。在任务的优先依赖关系条件下，并行应用任务集的向上优先等级自DAG 任务集的出口节点开始递归向上进行计算，记为ζ。任务τi的ζ值等于其后继任务与τi之间的通信成本之和的最大值加上其在所有VMs上的平均计算成本，其计算表达式如下：

式中：wi为任务τi的平均执行时间，可通过式（17）计算：

同理，任务τi的向下优先等级(τi)的计算表达式如下：

3.4 能耗预分配

定义5可改进能量。在用户给定能耗约束且当前工作流的最小能耗已知时，工作流的可改进能量Eadv(G)表达式如下：

定义6预算等级（BL）。工作流能耗的可支配部分将按照每个任务不同的BL等级进行分配，任务的BL计算如下：

工作流中任务τi初始给定的BL预算等级能耗EBL(τi)由其预算等级BL和最小能耗等因素决定，其计算式如下：

在极端情况下，任务的预分配能耗也始终不能超过其能耗上限，因此任务的预分配能耗Ebdgt(τi)应满足：

设定一个等待调度的并行应用任务集Seq(G)，该任务集按照ζ值降序排列的调度序列为{τs(1),τs(2),…,τs(|N|)}，设定当前的待调度任务为τseq(j)，则{τs(1),τs(2),…,τs(j-1)}表示已调度完成的任务集合；{τs(j+1),τs(j+2),…,τs(|N|)}为未被调度的任务集合，此时任务集的总能耗为：

工作流的实际总能耗必须小于等于其能耗约束，即Eseq(j)(G)≤Ebdgt(G)。可以得到：

根据式（24）可得出将任务集总能耗约束分摊给每个单独任务的方法，则序列中当前待调度任务的能耗约束为：

式（25）使任务集总能耗约束传递给每个任务，并降低了算法时间及复杂度。

3.5 调度长度最小化算法

具有能耗约束的工作流调度长度最小化算法（BLMSL）的伪代码如算法1所示。

步骤1 计算任务集中所有任务的ζ值和值，这是BL预分配策略的基础，并根据ζ值降序排列得到任务的调度队列。步骤3 计算每个任务的BL值和所能消耗的最小和最大能量。步骤4～5 计算工作流的最小最大能耗以及可改进能耗Eadv(G)，并根据可改进能耗计算出任务的Ebdgt(τi)。步骤10～27 将任务依次出队进行调度，确定每个任务的能耗约束Egiven(τi)，并选择该能耗约束下具有最小调度长度的VM和频率组合。其中步骤13～26 为队列中的任务选择合适的VM与频率，直至队列中所有任务均完成调度。步骤29 和30 分别统计工作流的实际总消耗能量Eact(G)和调度长度SL(G)。

遍历任务队列中的所有任务的时间消耗为O(N)，对于就绪任务队列中的每个任务，遍历所有VM和频率组合为其选择满足能耗约束且具有最小EFT的VM的时间复杂度为O(|N|×|VM|×|F|)，其中|F|表示从k,low 到k,max的离散频率数量。因此，可以得出BLMSL 算法的时间复杂度为O(|N|2×|VM|×|F|)。

算法1BLMSL 调度算法

输入：G=(N,E,C,W)，VM，Egiven(G)；

输出：E(G)，SL(G)。

2:fori←1 to|N|do；

3:计算Emin(τi) 、Emax(τi)和BL(τi)；

4:计算工作流图的Emin(G)、Emax(G)；

5:计算工作流图的Eadv(G)；

6:end for

7:fori←1 to|N|do

8:计算EBL(τi)和Ebdgt(τi)；

9:工作流图G根据节点的ζ值降序排列得到任务优先队列Seq(G)

10:while 队列Seq(G)非空

11:τtmp= 队头节点

12:计算Egiven(τi)；

13:for eachvmk∈VMdo

15:计算Eact(τi,vmk,k,h)；

16:ifEact(τi,vmk,k,h) ＞Egiven(τi) then

17:continue；

18:end if

19:计算Eact(τi,vmk,k,h)；

20:ifEFT(τi,vmk,k,h)＜AFT(τi)

21:vmpr(i)←vmkandpr(i),hz(i)←k,h

22:Eact(τi,vmpr(i),pr(i),hz(i)) ←E(τi,vmk,k,h)

23:AFT(τi) ←EFT(τi,vmk,k,h)

24:end if

25:end for

26:end for

27:end while

28:end for

29:计算Eact(G)；

30:计算SL(G) ←AFT(τexit)；

31:returnE(G)，SL(G)

3.6 调度实例分析

本节使用图1 中的DAG 图来进行本文实验，表2 列出了VM的相关参数，如动态功率、有效开关电容和动态功率指数等。能耗约束值Ebdgt(G)设置为Emax(G)×λ，λ的取值为0.5。当MSLECC 算法使用表2所示参数的VM调度图1 中的任务集时，其总调度长度是129.525 6。

表2 VM 的功率参数Table 2 VM power parameters

在相同配置的情况下，表3 显示了BLMSL 算法在图1所示的任务集中总调度长度为85.852 4，所消耗能耗为71.739 2。相比MSLECC 算法，BLMSL 算法的调度长度减少了33.73%，能量消耗减少了9.04%，使得工作流的调度长度和能耗都得到优化。

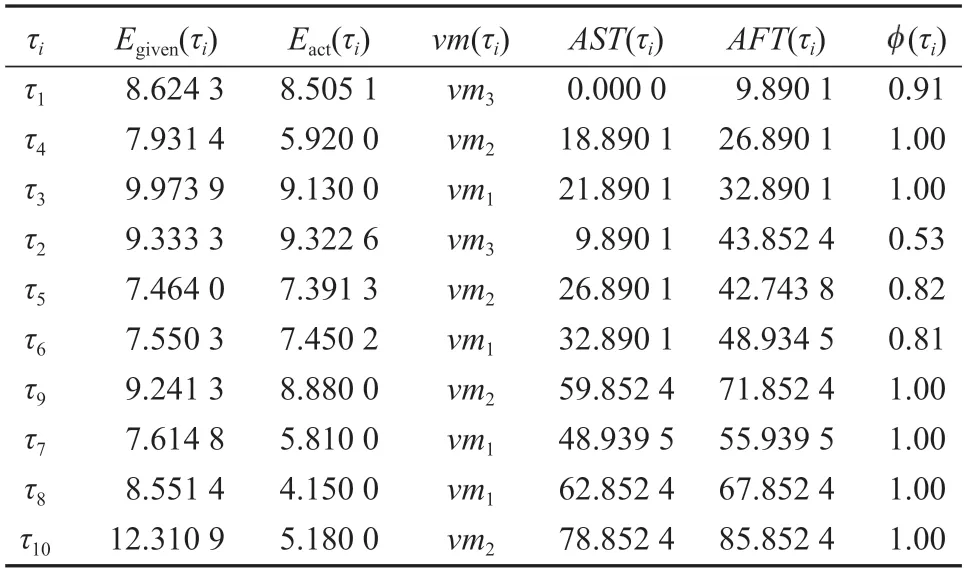
表3 使用BLMSL 算法在图1所示的并行应用分配结果Table 3 Parallel application allocation results as shown in Fig.1 using BLMSL algorithm

使用BLMSL 算法调度图1 中任务集的结果如图2所示，调度长度为85.852 4。

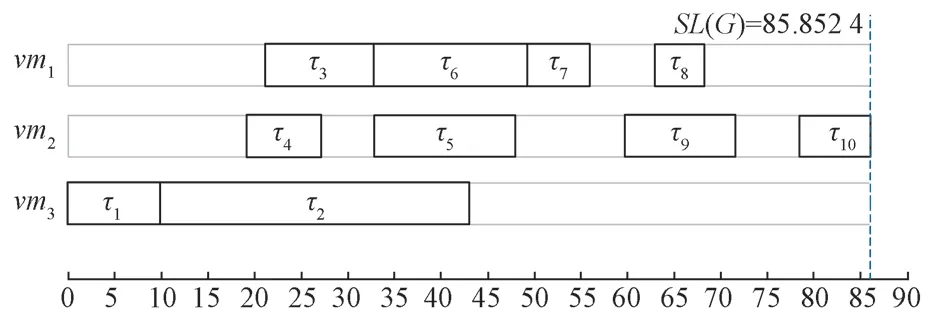
图2 BLMSL 算法的调度效果图Fig.2 Scheduling effect diagram of BLMSL algorithm

4 实验结果及分析

本节进行了多组实验来对比观察BLMSL 算法相较于其它先进算法的性能。首先介绍实验设置，然后给出实验结果及分析。

4.1 实验设置

实验中工作站配置了Intel Core(TM) i5-9300H@2.40GHz 八核处理器，16 GB 内存，系统运行版本为Windows10，采用Python 作为实验的编程语言。模拟的HCS 具有64 个计算能力和单价各异的VM。VM的主要参数如下：10 ms ≤wi,k≤100 ms，10 ms ≤ci,j≤100 ms，0.03 ≤Pk,ind≤0.07，2.5 ≤mk≤3.0，k,max=1.0 GHz。所有的频率均为离散值，精度为0.01 GHz。

HEFT 算法是异构系统上以减少调度长度为目标的经典算法，MSLECC 算法与本文的工作均为在考虑能耗约束的前提下最小化调度长度，因此选择这两种算法作为实验中的对比算法。这3 种算法的研究目标均是最小化工作流的调度长度。

本文的实验使用实际的能耗E(G)和最终的调度长度SL(G)作为算法性能的评价指标，使用高性能计算领域中广泛使用的真实应用并行任务集进行测试，通过改变应用规模的大小和能耗约束的大小来更直观地说明BLMSL 算法的有效性。

4.2 Epigenomics 工作流应用

本节选择生物遗传学领域的表观基因组学Epigenomics作为测试的工作流结构，下文中简称EP，其科学工作流应用程序的结构如图3所示。

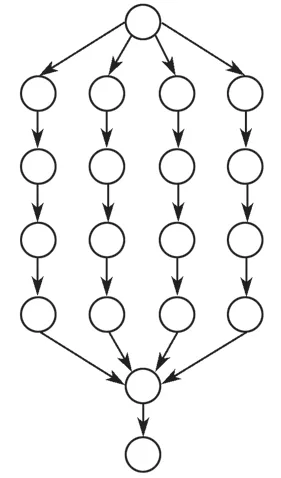
图3 Epigenomics工作流结构图Fig.3 Epigenomics workflow structure diagram

实验一。本组实验工作流的能耗约束固定为0.5（即Egiven(G)=Emax(G)×0.5）， 将EP 应用的规模分别设置为19,51,103,523,1 003，随后比较在不同任务数量时不同算法的实际能量消耗和调度长度。MSLECC 算法和BLMSL 算法在所有的实验案例中都能在满足能耗约束的前提下成功进行调度，而由于HEFT 算法不考虑功耗约束，虽然实现了较小的调度长度，但其能耗未能满足能量约束条件。

表4 展示了3 种算法在不同任务数量下的实际能耗和调度长度。随着工作流应用程序规模扩大，能耗和调度长度随之增大。相比HEFT 和MSLECC 算法，BLMSL 能够保证在满足能耗约束的条件下，获得较小的调度长度，在应用规模为N=1 003 且消耗能量基本相同的情况下，BLMSL 算法相比MSLECC 算法调度长度减少了约63.22%，体现了其在调度长度最小化方面的巨大优越性。

表4 不同应用规模下的EP 工作流调度结果Table 4 EP workflow scheduling results under different application scales

图4 展示了3 种算法在不同任务数量的EP 应用下的调度长度结果，发现BLMSL 算法在满足能耗约束条件下，实现了较其他算法更小的调度长度。

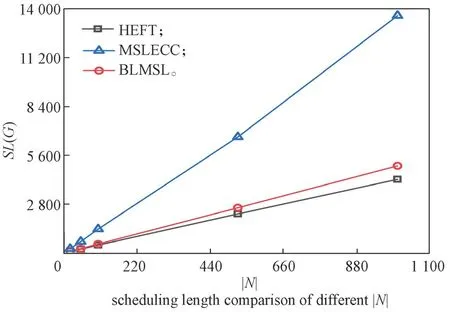
图4 不同任务数的SL 对比Fig.4 SL comparison of with different task numbers

4.3 Inspiral 工作流应用

本组实验采用重力物理学领域的LIGO 科学工作流，其结构如图5所示。

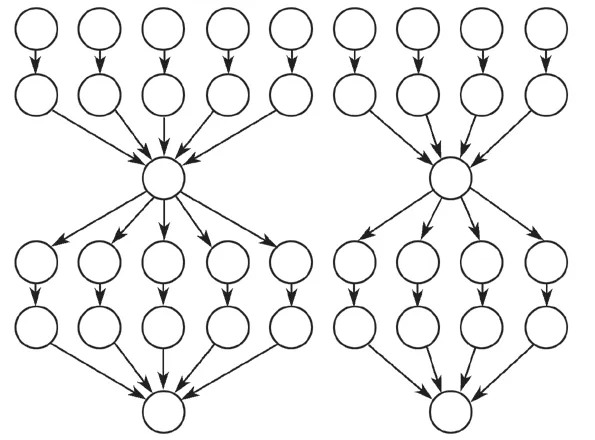
图5 Inspiral 工作流结构图Fig.5 Inspiral workflow structure digram

实验二。将实验的应用规模固定为94，能耗约束值Egiven(G)计算为Emin(G)×λ，λ的取值从2 到4，取值间隔为0.5。

详细调度结果见表5，当给定能耗较宽松时，工作流中任务能利用更宽松能量实现更小调度长度，λ=4.0，BLMSL 算法在满足能耗约束条件下，实际调度长度和HEFT 算法仅相差3.72%，而能量消耗却比HEFT 算法节省13.47%。当并行应用任务集给定能耗较小时，BLMSL 算法的优越性更突出，如λ=2 时，BLMSL算法实际调度长度比MSLECC 算法提升了76.49%。

表5 不同能耗约束条件下的LIGO 工作流调度结果Table 5 LIGO workflow scheduling results under different energy consumption constraints

图6 显示了不同能耗约束的LIGO 应用下3 种算法的调度长度结果。从图中可以观察出，BLMSL算法在给定能耗条件变化较大的环境下依然能保持调度长度的相对稳定。且在不同能耗约束条件下，BLMSL 算法的最终调度长度值始终小于MSLECC算法的调度长度值。

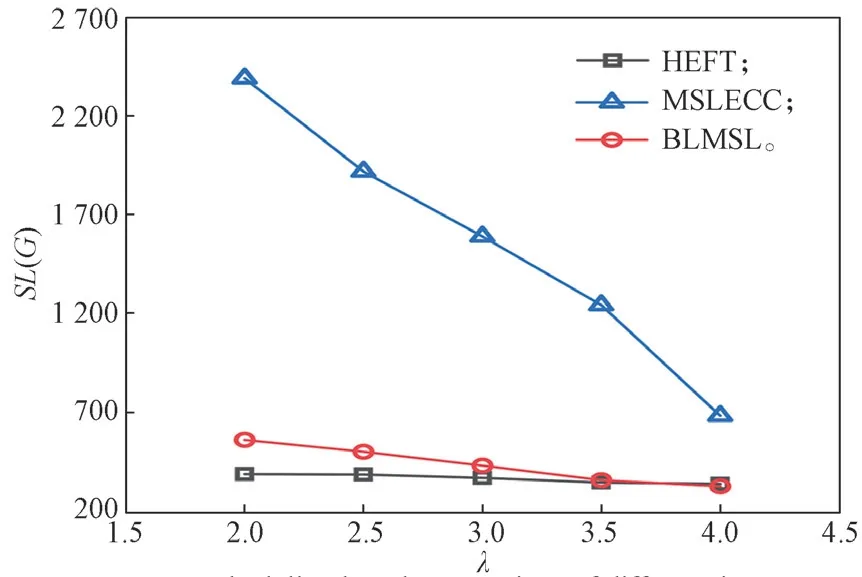
图6 不同能耗约束LIGO 的SL 对比Fig.6 SL comparison of LIGO with different energy consumption constraints

由以上结果可看出，BLMSL 算法能够同时兼顾工作流的能耗和调度长度两方面，实现性能平衡。通过观察在LIGO 和EP 并行应用科学工作流上进行的诸多实验，充分说明BLMSL 算法在两个科学工作流上的实验中始终保持着优越的性能。

5 结语

针对HCS 中能量受限并行应用的调度长度最小化问题，本文设计了BL等级预分配机制，并基于BL等级预分配策略提出了BLMSL 算法来实现算法的调度长度最小化，提升了能耗预分配阶段的合理性和科学性，避免了因对任务优先级敏感而影响调度长度问题。在多个科学工作流上进行实验的结果表明，BLMSL 算法能在能耗约束的条件下实现更小的调度长度。未来，课题组将致力于探索云环境中工作流集在预算约束下的高可靠性研究方法。