基于自稳隐形拱理论的巷道支护研究

王同光 WANG Tong-guang

（中煤西安设计工程有限责任公司，西安 710054）

0 引言

随着煤矿开采深度的增加，开采活动逐渐扩展到地质条件更为复杂的区域[1]。现有的一些井下支护措施虽然可以满足生产需求，但由于缺乏科学依据，无法充分发挥经济效益[2，3]。

基于自稳隐形拱理论的锚杆支护设计在一般围岩巷道取得了良好的支护效果[4-6]。在研究中，胡鹏等[7]以自稳隐形拱理论为基础，针对矩形巷道进行了改进，设计了导硐法掘进的刚柔双层网支护的圆弧角矩形切眼。高健铭等[8]以自稳隐形拱理论为基础，通过计算得出黄陵矿业一号煤矿六盘区回采巷道围岩控制的支护参数，并利用计算机数值模拟软件进行多次迭代计算，测定了巷道围岩的松动圈范围。王磊等[9]应用自稳隐形拱理论，将岩体承载能力的界限纳入锚索锚固范围内，将支护策略由被动支护转为主动支护，并进行了支护参数的优化。郑选荣[10]在陕北榆阳煤矿2302运输巷道中，使用FLAC数值模拟软件和自稳隐形拱理论，对巷道的掘进断面和支护方案进行了优化。这些研究通过应用自稳隐形拱理论，对巷道的设计和支护方案进行了改进和优化，为巷道工程的安全施工提供了指导和参考[11，12]。

本文以陕北可可盖煤矿巷道的断面形式和原有支护方案为基础，基于自稳隐形拱理论进行了支护参数计算，并运用FLAC软件进行了验证与分析，以此得到合理的自稳隐形拱支护方案，提高工程的安全性和经济效益。

1 自稳隐形拱锚杆支护理论

自稳隐形拱理论的基本观点首次将岩体的承载能力的界限划定为破坏岩体。该理论认为岩体的破坏不仅与是否达到塑性有关，还认为即使松散的围岩达到塑性破坏后仍然具有一定的承载能力[13，14]。

图1为岩石的应力-应变曲线，可以看出，岩石在受到压力后仍然具有一定的强度，即使达到塑性也仍然具有一定的承载能力。

图1 岩石应力-应变曲线

地下硐室的围岩在开挖之后会发生塑性变形甚至断裂破坏。然而，如果开挖后的巷道顶板上的围岩单元体处于挤压状态，它们仍然具有一定的承载能力。将顶板内拉应力为零的单元体相连，得到的连线形成的曲线在平面应变问题中呈现为一个椭圆形，该椭圆形曲线被称为自稳隐形拱。

巷道围岩不稳定区划如图2所示。可以看出，在大多数情况下，产生塑性破坏的围岩体仍然被视为岩体的承载主体；而巷道的稳定是由于巷道顶部存在自稳隐形拱。

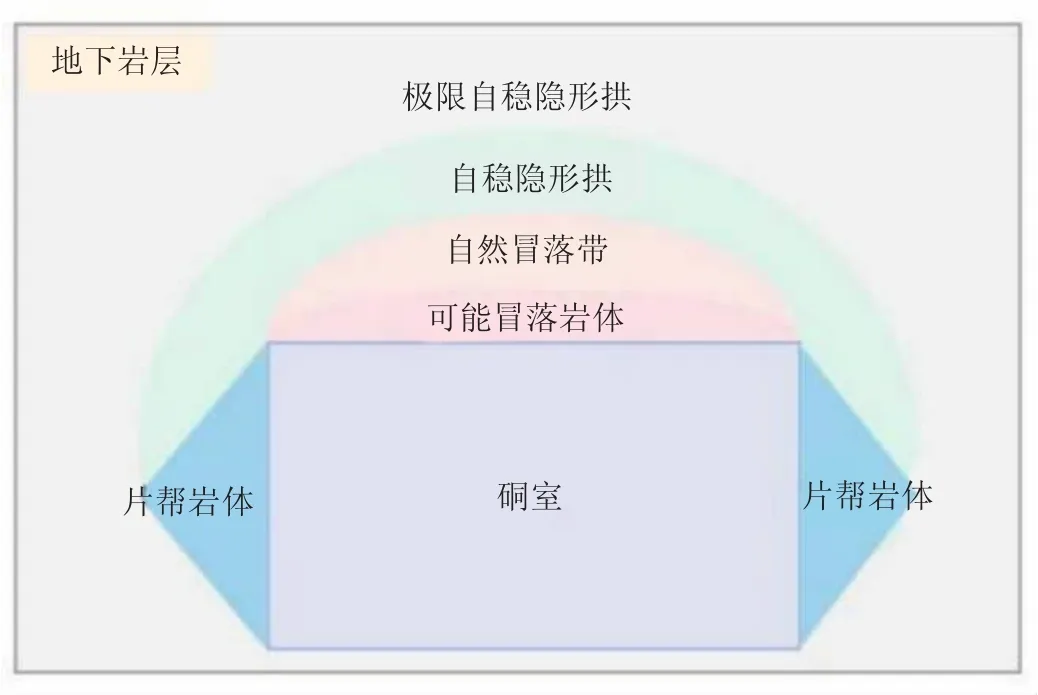
图2 巷道围岩不稳定区划

图3为帮锚对自稳隐形拱的影响，可以看出，有效的支护可以将顶部的压力转移到两侧帮部深部。如果在隧道开挖后，在帮部采用预应力锚杆支护使其变为类似刚性结构，那么极限的自稳隐形拱现象就会消失。没有极限的自稳隐形拱，隧道围岩的不稳定区域就会大大减少。

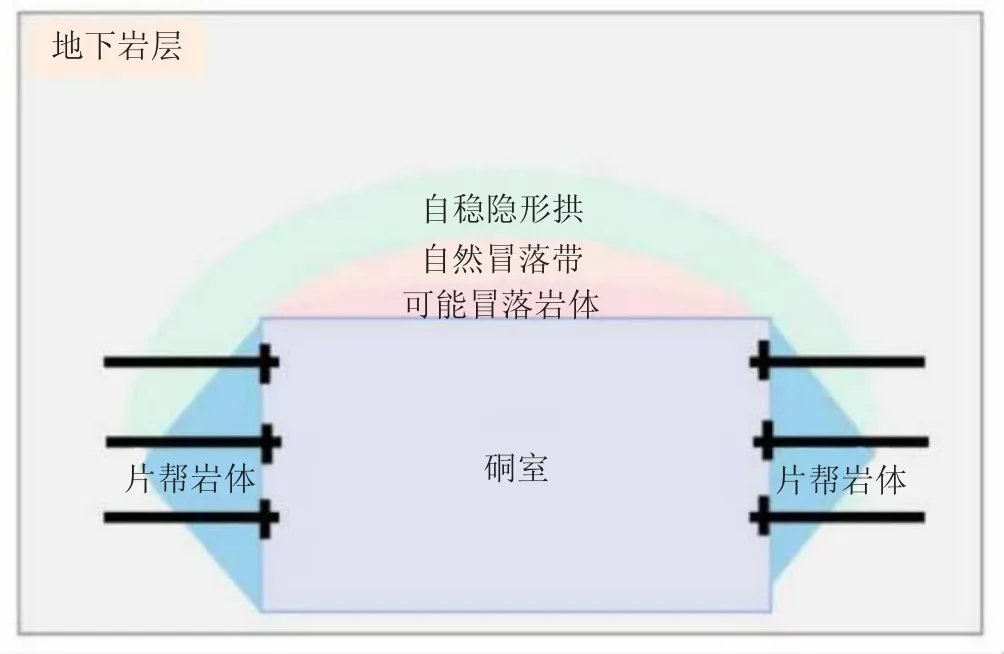
图3 帮锚对自稳隐形拱的影响

隧道顶部锚杆的加固作用也可以改变自稳隐形拱的大小。图4为顶锚对自稳隐形拱的影响，可以看出，采用预应力锚杆支护来改变巷道顶部的自稳隐形拱变形对围岩的加固效果，会形成较小的新的二次、三次隐形承载拱。随着自稳隐形拱不断变小，巷道顶板的稳定性增加，从而大大减小了巷道围岩的不稳定区域。

图4 顶锚对自稳隐形拱的影响

2 自稳隐形拱计算方法

依据自稳隐形拱的定义，巷道顶部应力应力单元中水平方向的拉应力均为零[15]。这一曲面的近似曲线方程为：

其中，

式中，W0为巷道顶板宽度，m；p0为巷道顶部垂直地压，MPa；σ2为顶板岩体的抗拉强度，MPa。

将自稳隐形拱方程转化为通式，则有：

式中，ha为巷道两帮起弧点距离底板的高度，m；hw为巷道的高度，m。

地下硐室开挖后，在无支护条件下，片帮岩体达到最大深度hw/2时，自稳隐形拱也会发展到最大，所对应的自稳隐形拱称为极限自稳隐形拱，其方程为：

极限自稳隐形拱是地下巷道围岩可能破坏的最大区间边界，对应的方程为：

其中，极限自稳隐形拱离顶板的最大高度为：

3 工程应用与实践

3.1 工程概况及地质特征

可可盖煤矿副斜井倾角6°，下山施工，每隔600m设50m的缓冲平段，斜长5305.3m。副斜井井筒采用明槽开挖+TBM工法施工，明槽段开挖长度290m，TBM掘进工法施工段长度5041.3m。

可可盖煤矿TBM基岩段围岩分级如表1所示。

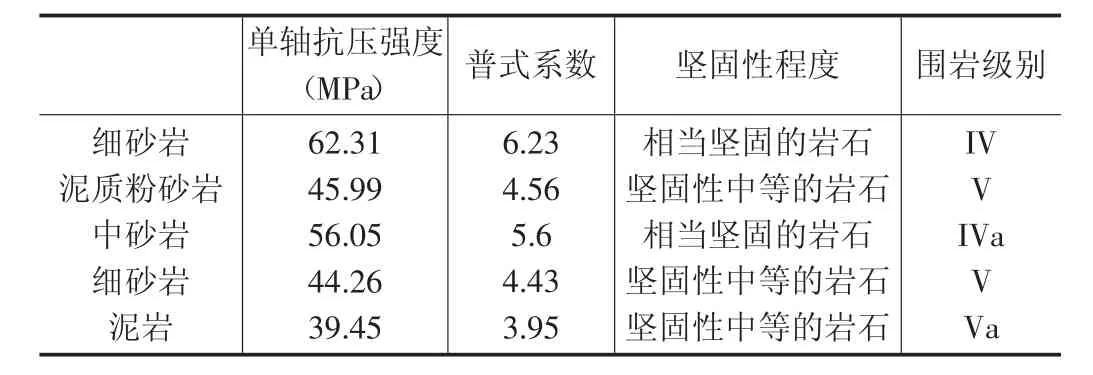
表1 TBM基岩段围岩分级

3.2 巷道支护参数的确定

由式（2）可知，当x=0时，

岩体抗拉强度取抗压强度的1/10，则巷道顶板最大隐形拱高度为：ymax=1.63m。

由式（10）计算可得极限隐形拱的最大高度为：ylid=3.53m。

根据自稳隐形拱曲线方程的计算，可以得到TBM基岩段巷道顶板的最大自稳隐形拱高度和极限隐形拱高度。当达到极限最大隐形拱高度时，普通的锚杆支护就难以达到理想的效果。在这种情况下，改选使用锚索进行支护更为合理。其中，锚杆采用HRB400钢筋，直径22mm，长度2400mm，间排距1000×1000mm；锚索采用直径为17.8mm的钢绞线，长度7300mm，沿井筒拱顶布置，间排距3000×3000mm；金属网采用直径为6.5mm的HPB300钢筋焊接，网格大小为100×100mm。

3.3 支护效果分析

鉴于本项目模拟的内容和特点，选用FLAC数值分析软件进行模拟。以可可盖煤矿主斜井明槽表土段为工程背景，模拟明槽段施工开挖并进行相应的支护模拟。模型尺寸（长×宽×高）50m×100m×45m，采用Mohr-Coulomb屈服准则模拟围岩变形。

从图5中可以看出，支护后的围岩顶板下沉量、底鼓量以及两帮移进量分别为15.932mm、7.64mm和12.502mm。根据这些数值可以得出结论，巷道开挖后围岩的变形稳定速度较快且变形较小。这表明采用锚网喷技术能够有效控制巷道顶板的下沉，并控制巷道两侧帮部的变形。在巷道的稳定阶段，顶板的最大下沉速率为0.25mm/d，而两侧帮部的最大变形速率为0.3mm/d。由于稳定阶段的变形速率非常小，围岩得到了良好的稳定。

图5 围岩表面位移

图6为采用十字布点法监测得到的巷道表面位移。

图6 位移-时间曲线

从图6可以看出，两侧帮部的最大位移量为105mm，而顶板的最大位移量为80.5mm。这些位移量均在设计允许的变形范围内，说明支护效果较为理想。对于个别地段出现顶板下沉较大的情况，可以考虑优化支护方案，增加锚杆长度或减小锚索间距，以提高锚索的抗变形能力，减缓顶板的冲击载荷作用，以此改善巷道的稳定性。

4 结论

根据自稳隐形拱理论推导的巷道锚杆支护技术设计思路，有效地提升了巷道的承载能力，防止了碎矸冒落，并扩大了自稳隐形拱理论的应用范围。在数值模拟和施工现场的监测数据中得到了可靠性的证明，应用自稳隐形拱理论进行巷道支护可以有效地控制围岩的变形，并为不良地层TBM施工中巷道锚网喷参数的设计提供了新的依据。