一种航天用分步预紧连接装置

□ 刘 寅

天津航天机电设备研究所 天津 300458

1 设计背景

从20世纪后期开始,世界各国开展深空探测活动日益频繁,探测目标的选择逐步转向小行星、火星等地外天体。在探测任务中,返回系统需要采集星体表面的土壤。在将土壤转运至返回器的过程中,需要一种装置能够分步传递推力至后续组件。在推力传递过程中,当推力达到要求数值时,先进行卸载,再继续传递推力。笔者根据整体功能的需求性,设计了一种航天用分步预紧连接装置。

2 结构设计

分步预紧连接装置主要由子套、调节螺钉、钢球、波簧、张紧套、导向帽、压簧、母套等部分组成。分步预紧连接装置结构如图1所示。

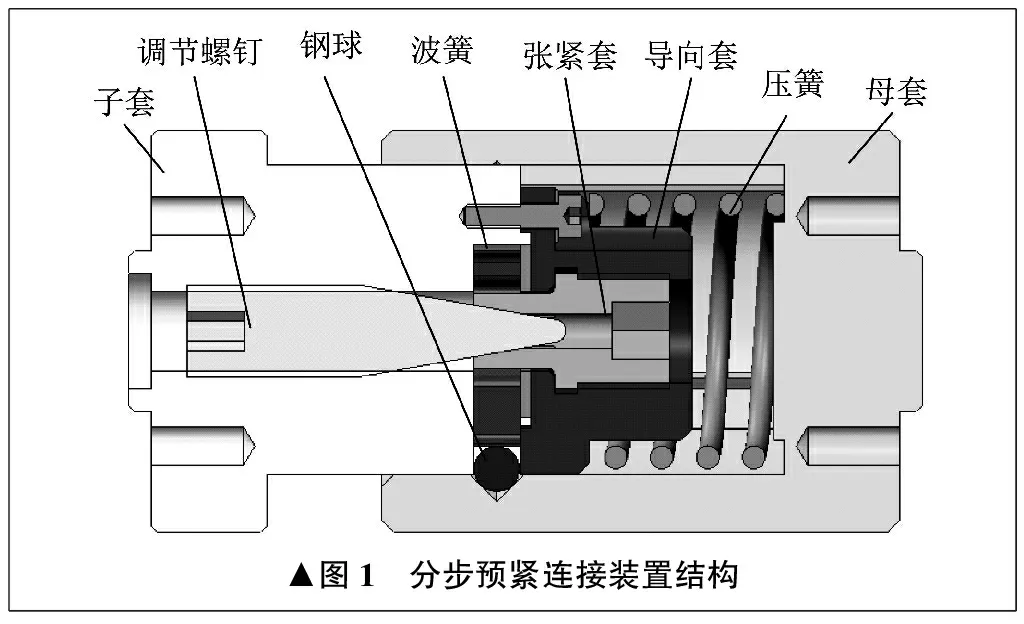
分步预紧连接装置中,子套和母套的作用是为前后组装提供接口。其中,子套的内侧为波簧提供装配和导向定位凹槽,母套的内侧为压簧提供轴向进给导向和收纳空间,并为钢球提供止推槽。子套如图2所示,母套如图3所示。

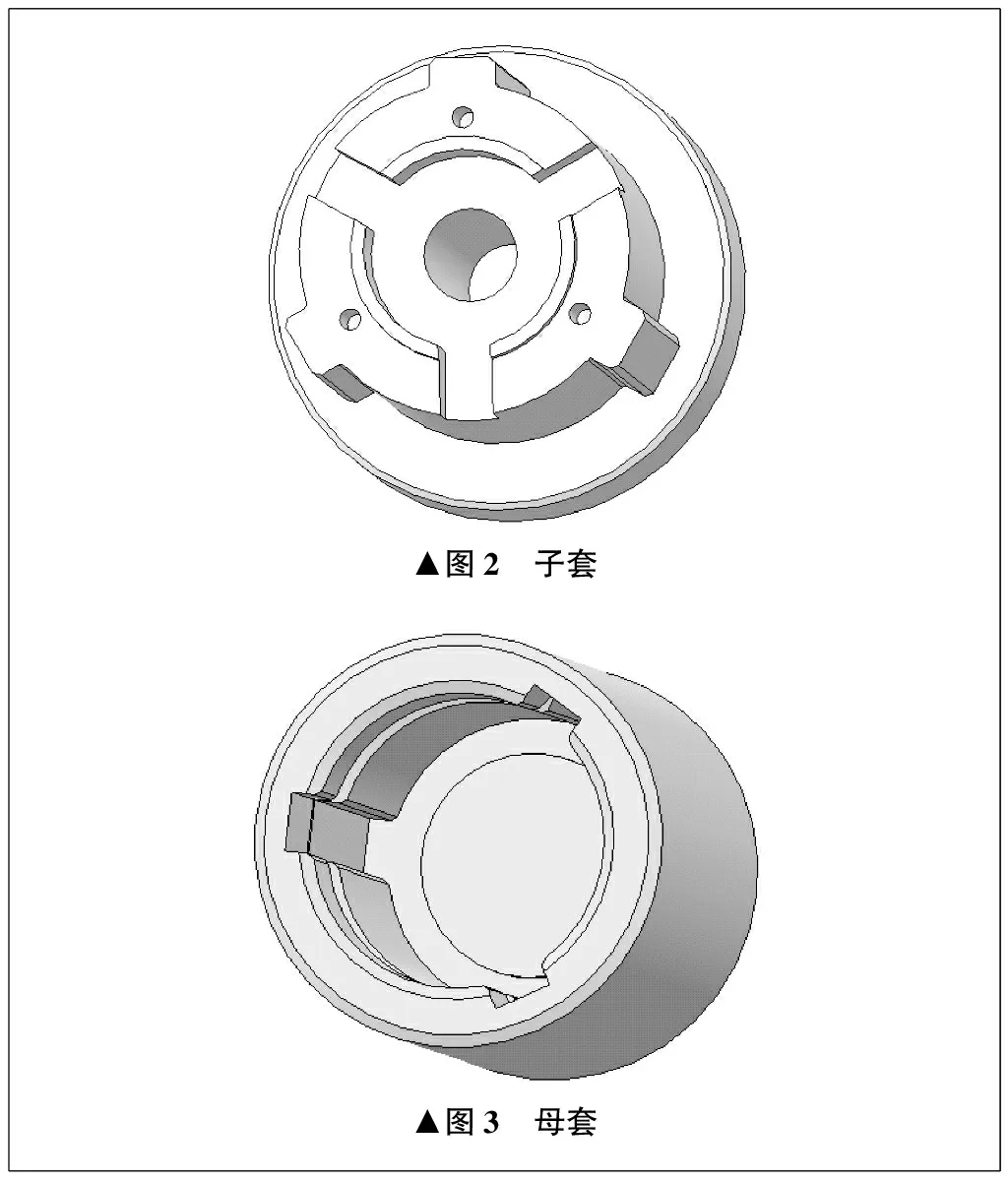
调节螺钉通过螺纹旋入张紧套,张紧套的外侧与波簧内侧接触。压簧和导向帽安装于母套内,压簧存在一定预紧力,用于向导向帽提供推力,通过调整垫片将波簧压紧在子套内。调节螺钉装配如图4所示。

3 工作原理

分步预紧连接装置的作用在于能够将输入推力分步传递给后续连接组件。在这一过程中,当第一段推力达到要求数值时,先进行卸载,使推力几乎归零之后,继续传递下一段推力。

分步预紧连接装置工作原理如图5所示。子套受到轴向推力传递给钢球。钢球受到母套凹槽向内推力作用,压缩波簧变形。波簧向内压缩,直至钢球自身移动到凹槽外。子套受到轴向推力作用,继续向前运动。压簧预设的预紧力可以防止子套带动前端零件一起产生惯性冲力,保证推进动作整体平稳。

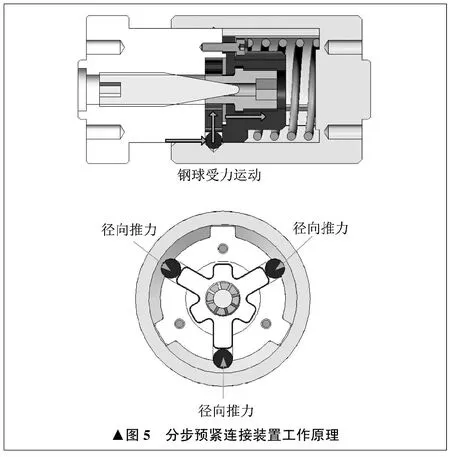
4 钢球受力计算

钢球在产生位移前,共受到来自三个方向的力,分别为系统给予的推力Fp、波簧给予的弹力Fs、凹槽给予的支反力Fz。其中,Fp与Fs成90°夹角,Fp、Fs均与Fz成135°夹角。材料之间存在润滑涂层,在忽略材料之间相对摩擦力的情况下,不难得出Fp和Fs受力大小相同。钢球受力分析如图6所示。

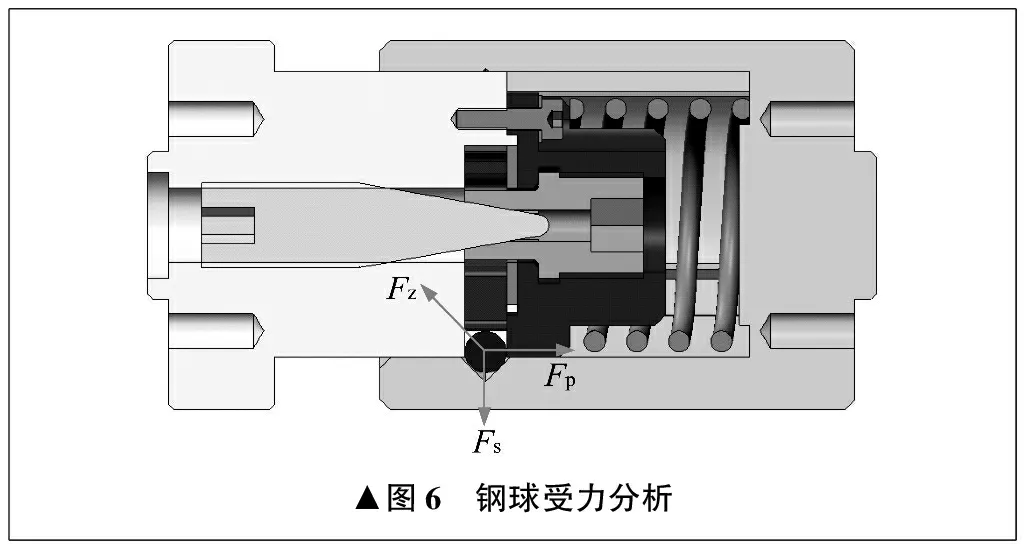
通过以上分析,将克服推力的计算问题转换为波簧弹力的固有属性设计。已知要求推力理论值为250 N,波簧弹力后期可以通过调节螺钉微量调节至最终数值。

5 波簧有限元分析

5.1 模型简化

分步预紧连接装置结构较为复杂,波簧产生大变形导致网格节点位移较大,系统矩阵必须以较小载荷步进行更新。由于接触较多,导致每一载荷步的迭代收敛速度较慢。为减少计算所需要的时间,仿真计算主体部分取1/6模型进行分析,如图7所示。为了验证模型分析可靠性,将对1/6模型分析的结果与对1/2模型和完整模型分析的结果相比较,1/2模型与完整模型分别如图8、图9所示,发现所得到的分析结果差距约为0.32%,因此可以认为此项简化并没有影响仿真结果。

5.2 接触与刚体设置

接触属性包括切向属性与法向属性。由于本次仿真分析产生的接触压力并不大,因此在法向压力上不设置上限值。在切向属性中设置摩擦因数,研究范围为0.05～0.3,中间每间隔0.05取一个值,不设置接触阻尼。

模型由球槽、钢球、波簧、下引导面、侧引导面五个部件组成,结构如图10所示。其中,钢球与球槽、波簧、侧引导面、下引导面之间存在接触,波簧与侧引导面、下引导面之间存在接触,共有六对接触。

由于侧引导面、下引导面、球槽的弹性变形对此次分析的影响均很小,因此可以忽略弹性变形,设置为刚体,以减小计算量,控制点设置在质心处。钢球的弹性变形直接影响接触角的大小与摩擦力的方向,波簧的弹性变形为整个模型提供拉脱阻力,所以将波簧设置为弹性体。

5.3 边界条件设置

仿真中,为了更好地模拟真实情况,采用两个分析步。第一个分析步将球槽向钢球靠近,在分析步结束时正好接触刚球。第一个分析步模拟的是钢球的装配过程,意义在于为第二个分析步中钢球与球槽的接触提供初始的分析条件。第二个分析步将引导面作为一个整体向上提升2 mm,此时钢球已从球槽中脱出,后续拉力不产生变化。

由于使用1/6模型,因此对称面处还需要设置对称约束,即约束对称面上的节点在垂直于面的方向上不产生位移,在平行于面的方向上不产生旋转。模型整体约束如图11所示,RP1点控制球槽位移,RP2点控制两个引导面位移。

5.4 分析结果

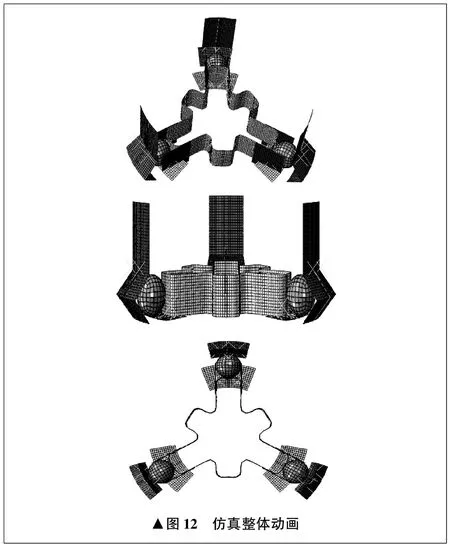
仿真整体动画如图 12所示。

拉力随钢球竖直位移变化如图13所示。

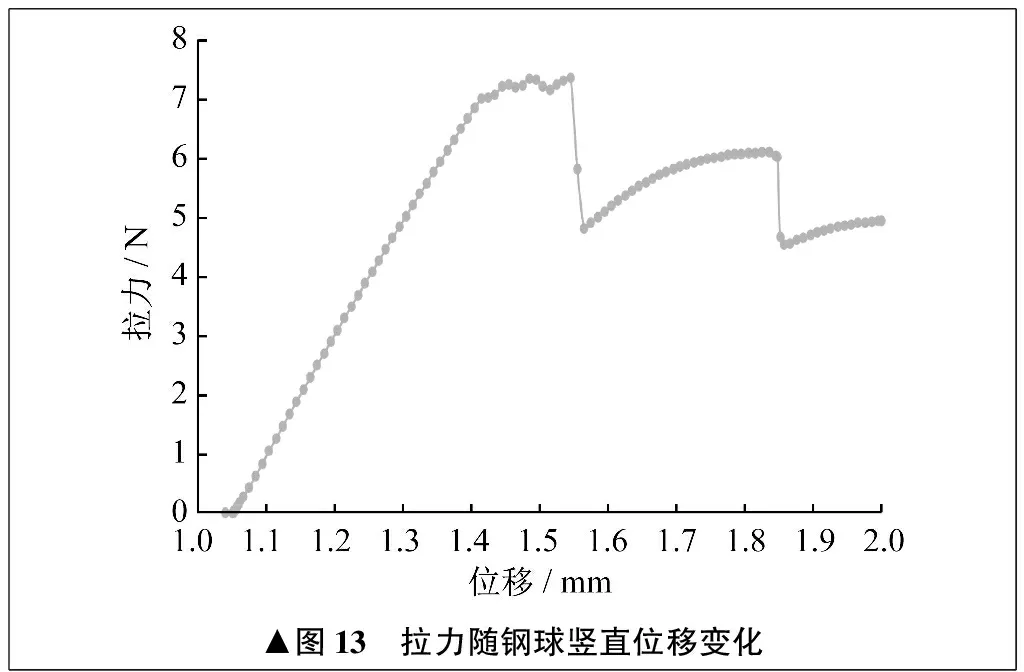
图13中前半部分近似为线性关系,说明波簧在端点处位移与弹性力的关系近似为正比例函数,后续的理论计算会用到这一结论。在后半段出现较大波动,原因是钢球在此时与球槽的拐角位置接触。接触点区域很小,在计算接触时较难准确得出接触力的大小,但是此时已经越过拉力值的最高点,所以不必给予过多关注。

6 参数优化

6.1 波簧厚度与拉力

从直观上来说,波簧厚度越小,弹性系数越小,在钢球行程相同的情况下,对钢球的弹性力也就越小,从而使整体机构更容易拉出。仿真也证实了这一点。仿真摩擦因数为0.1,计算一组不同厚度的波簧所需要的拉力,无中心预紧,结果如图14、表1所示。

表1 波簧厚度与拉力关系

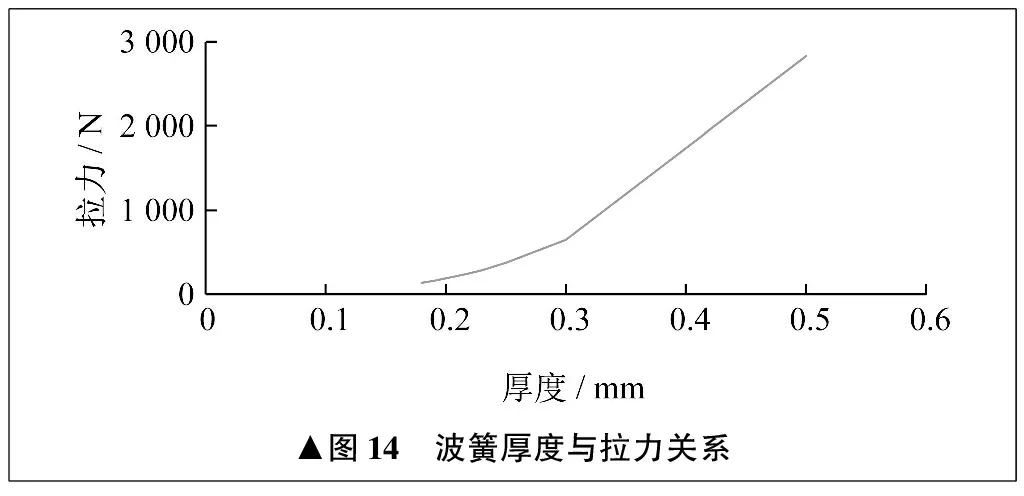
从结果中可以发现,当波簧厚度为0.22 mm时,所需要的拉力为250.28 N,小于280 N,为螺栓调整留下余地。因此,在不改变弹簧形状的情况下,倾向于将波簧厚度调整为0.22 mm。

5.2 摩擦因数与拉力

从直观上来说,摩擦因数越大,使机构拉出的弹性力也越大。波簧厚度为0.20 mm与0.22 mm,仿真计算两组不同摩擦因数与拉力关系,无中心预紧,结果如图15、表2所示。

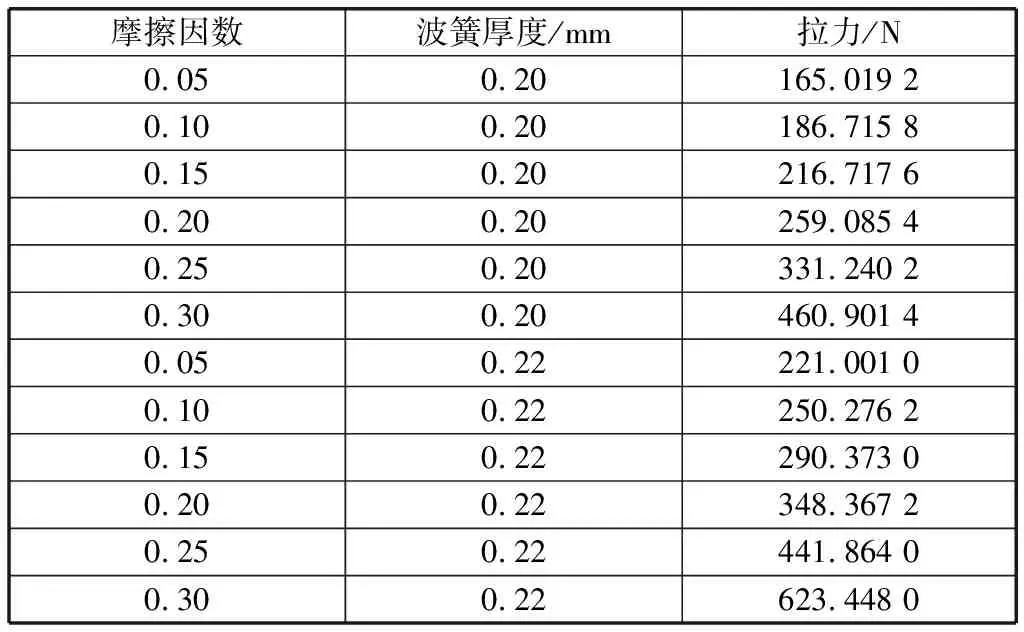
表2 摩擦因数与拉力关系

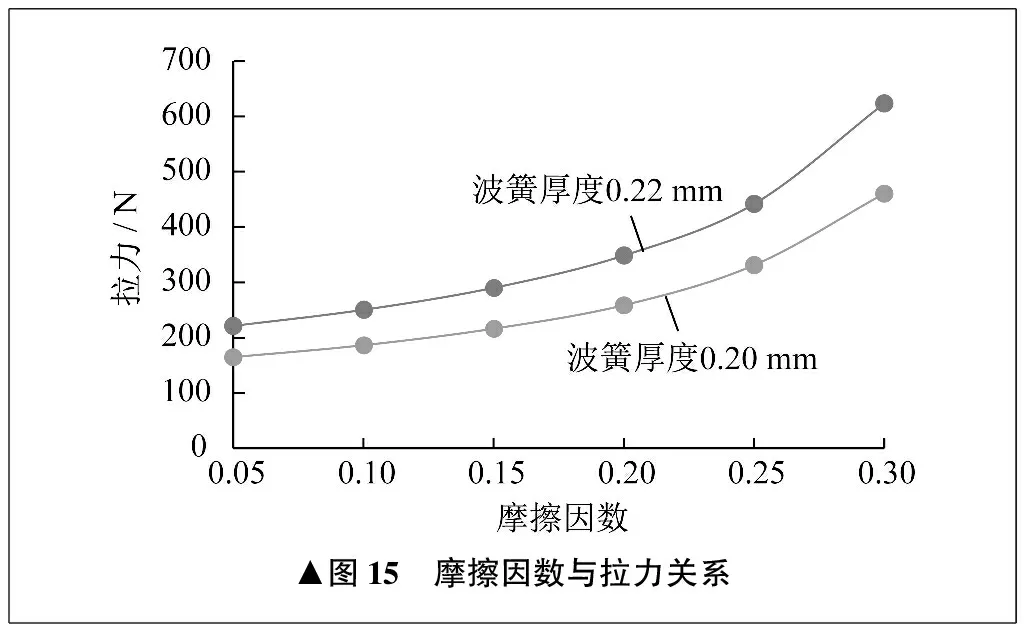
从结果中可以发现,模型对于摩擦因数较为敏感,在摩擦因数变化0.05的范围内,拉力大小改变约为40 N,波簧厚度越大,拉力改变越大。

7 结束语

笔者设计了一种航天用分步预紧连接装置,通过理论计算、有限元仿真、参数优化三种方法得到解锁边界条件的极限推力,满足分步预紧的功能要求。