基于表面及迎风面改性的锯齿翅片强化传热研究

2023-12-12张西龙张永亮董文林房玉宝

制冷学报 2023年6期

张西龙侯硕张永亮董文林房玉宝

(青岛理工大学机械与汽车工程学院青岛 266520)

散热器广泛应用于汽车、空调、电子产品以及化工等领域,随着人们对散热器设计提出紧凑、高效、经济等更高要求,强化传热技术应运而生。强化传热的途径主要有增加传热面积,增大传热温差和提高传热系数,而翅片作为散热器的重要组成部分,众多学者[1-4]对其进行了研究,通过结构改进及参数优化来提高传热系数以实现强化传热,但同时也伴随着较大的压降损失。

鲁亚龙等[5]将平直翅片改为弧形,朱行[6]将平直翅片改为波纹型,改进后的翅片较平直翅片传热性能提高约15%。Ke Hanbing等[7]对比了平直和波纹翅片管换热器性能的差异,与平直翅片相比,波纹翅片的热边界层会不断被破坏,从而提高换热性能。曾炜杰等[8]分析了圆柱型翅片管换热器变工况下的换热性能。郝鸿伟等[9]提出了一种新型波纹-锯齿翅片,传热性能较传统翅片可提高约30%。除改变翅片形状来强化传热外,翅片表面结构和尺寸优化也是研究强化传热的方向之一。Chen Chaowei等[10]对平直翅片进行打孔,多孔翅片不仅可以增强传热,还能有效降低压降。陈梦杰等[11-12]在翅片表面引入凸起和凹窝来强化换热,整体换热性能均有不同程度的提高。敬文娟等[13]综合考虑了孔大小、孔数量、孔布局以及孔形状等结构参数对换热性能的影响。

上述研究表明,无论是改变翅片形状还是表面处理,都实现了强化传热,但在不同截面通道内嵌入翅片后,所得结果有所不同。李鹏程等[14]对石墨管内嵌入扇形翅片进行了数值模拟,结果表明,角度布置为45°时强化换热的效果最佳。A. Vaisi等[15]分析了波纹翅片和带状翅片不同结构参数对换热的影响,两换热面之比接近1时,热性能系数最好。Lan Yongqi等[16]设计了一种带有截断偏移翅片的新型微通道,数值结果表明,过大偏移值会抑制热增强。因此,要想散热通道达到最佳换热的效果,嵌入的翅片需适当的参数值,否则不但不利于强化传热反而会带来较大的压降损失。

基于上述分析可知,在对翅片进行强化传热研究时,虽然研究范围很广结论也不尽相同,但在对翅片表面进行强化研究时主要是围绕平直翅片,而对本身散热性能更好的锯齿型翅片表面强化传热的研究较少。本文以锯齿型翅片为研究对象,通过改进翅片表面及迎风面结构使得新型锯齿型翅片在平均压降损失几乎没有变化的情况下,传热性能和综合性能均得到提升,达到强化传热的目的。

1 数值模型的描述及方法

1.1 散热器模型简化

利用散热器结构的周期性和对称性,取一个周期上的结构单元建立单元体模型,如图1(a)所示,结构示意图及尺寸参数如图1(b)所示,其中散热单元长度L=50 mm,宽度D=4.4 mm,翅片间距d0=2 mm,原点位于单元体模型的正中间。为实现强化传热的目的,在翅片表面设置不同形状的凹槽和凸起,具体结构及尺寸如图2和表1所示。

表1 翅片几何参数

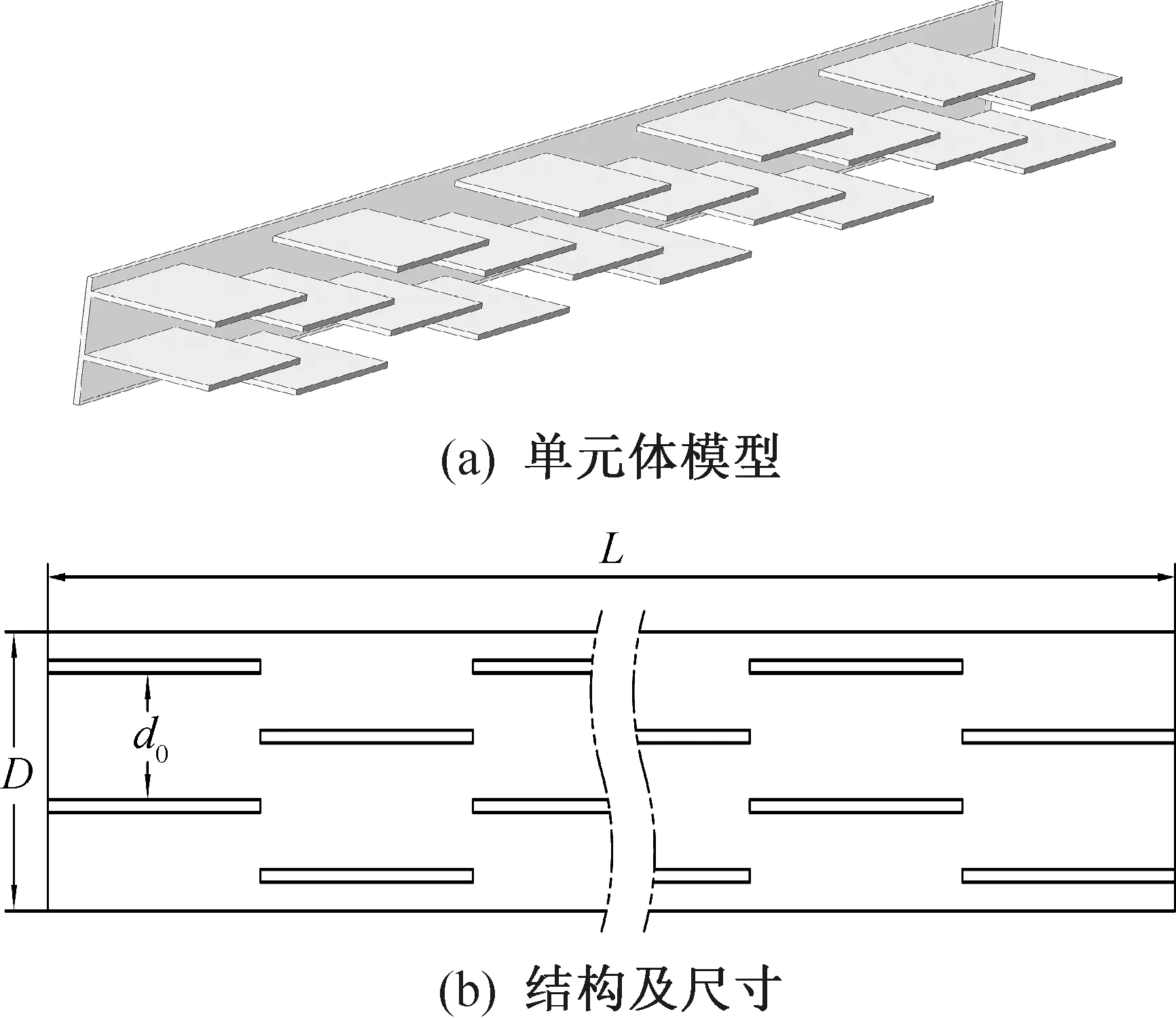
图1 元体模型及其结构

图2 改进后单个翅片结构

1.2 控制方程及数据处理

流体在流动与传热的过程中,要满足3大控制方程,即质量守恒方程、动量守恒方程和能量守恒方程,控制方程的通用形式为[17]:

(1)

式中:ρ为流体密度,kg/m3;Φ为通用变量,可代表u、υ、T等求解变量,单位分别为m/s、m/s、K;t为时间,s;U为速度,m/s;ΓΦ为广义扩散系数;SΦ为广义源项。针对特定的方程,Φ、Γ、S具有特定的形式。

通道截面的水力直径[18]:

(2)

式中:dh为水力直径,m;d为翅片高度,mm;d0为翅片间距,mm;b为翅片厚度,mm。

流动雷诺数:

Re=ρυdh/μ

(3)

式中:υ为流体速度,m/s;μ为流体的动力粘度,N·s/m2。

努塞尔数:

Nu=hdh/k

(4)

式中:h为对流换热表面传热系数,W/(m2·K);k为静止流体导热系数,W/(m·K)。

压降损失:

咳嗽跟呼吸的空气有很大关系。如果空气太脏，或者是太干燥，宝宝就咳得厉害。所以，在家里护理宝宝时，若天气好，应多开门窗通气，使屋里的空气保持清新；若天气不好，可以使用空气净化器来改善室内的空气；若空气干燥，要用加湿器增加室内湿度，使用加湿器使室内湿度保持在40%～50%，湿度太大也不行，容易使房间滋生霉菌。也可以选择让宝宝吸入水蒸汽的方式缓解咳嗽。睡前在浴室内放会儿热水，待蒸汽充满浴室，把宝宝抱进去尽可能多待一些时间，让呼吸道通过多吸入一些水蒸汽获得充分的滋润，这个方法也有助于缓解鼻塞和咳嗽。还可以用妈妈们蒸脸的蒸汽机让宝宝的呼吸道滋润，但蒸汽机里不能使用自来水或矿泉水，要使用蒸馏水。

Δp=p1-p2

(5)

式中:p1、p2分别为进、出口平均压力,Pa。

翅片气侧摩擦因子:

(6)

综合性能评价指标[19]:

(7)

式中:下标0代表传统锯齿型翅片;i代表改进结构后的锯齿型翅片,分别可取1(矩形)、2(圆形)、3(三角形)。

1.3 边界条件设置

计算域和边界条件如图3所示,来流速度分别为2、4、6、8、10 m/s,来流温度为300 K。翅片壁面设置为恒温壁面,温度为363 K,其余壁面为绝热条件。空气域上下两面设置为周期性边界条件,翅片和空气域的正面设置为对称边界条件。同时,为防止热回流,空气域进、出口分别延长5 mm 和15 mm。

图3 边界条件

1.4 网格划分及独立性验证

利用ANSYS Workbench 中的Fluent Meshing模块对散热单元进行网格划分,如图4所示。为提高数值模拟时在凹槽和凸起位置的准确性,采用局部网格加密并在空气域与翅片交界面位置添加边界层的方法。同时为保证计算精度,网格独立性验证结果如表2所示,通过网格独立性验证发现,网格数为1 181 035时的Nu和Δp与网格数为2 222 811时的相差约2%,所以综合考虑本文最终采用1 181 035个网格进行仿真分析。

表2 网格独立性验证

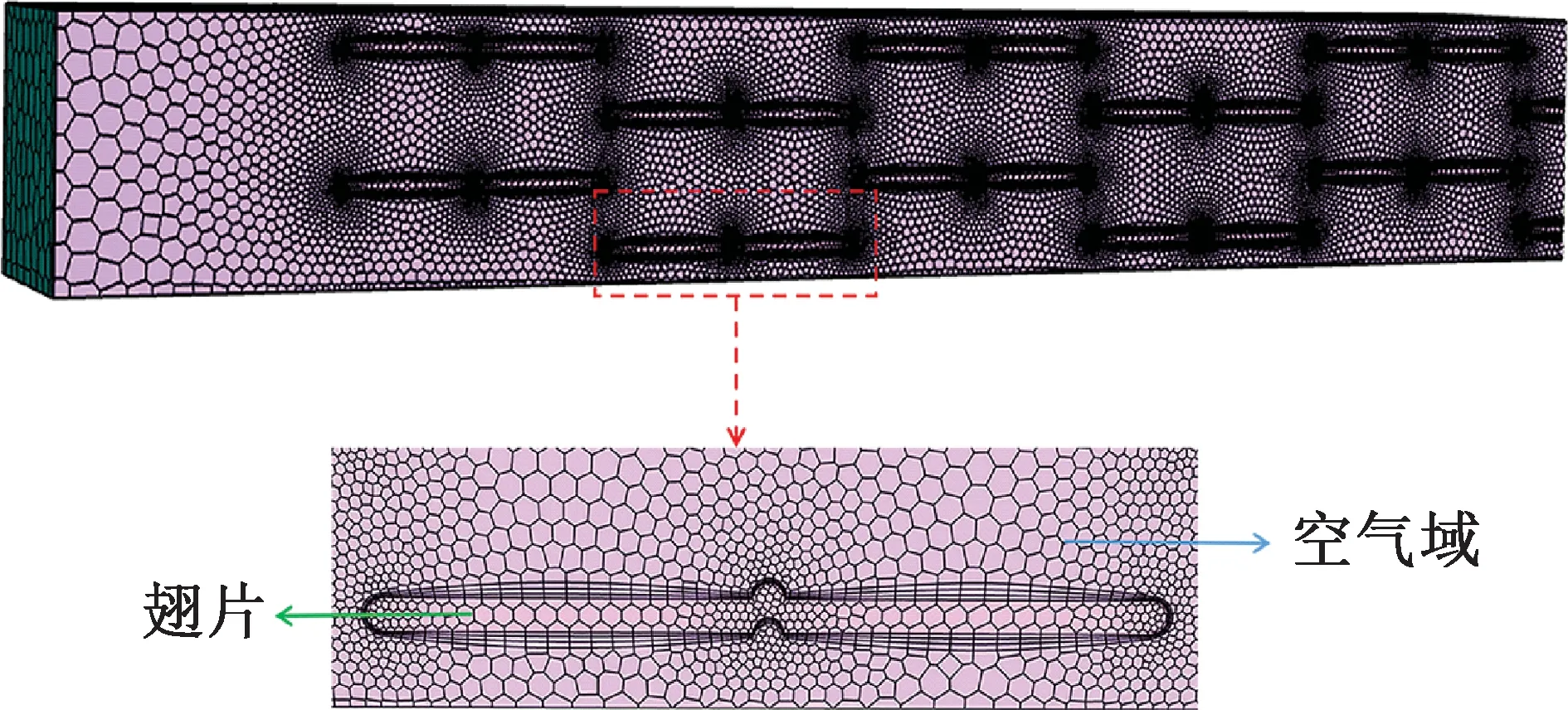
图4 网格划分及局部网格放大

1.5 模型验证

为验证模型的正确性,将本文数值模拟得到的数据与文献[20]中的实验数据进行对比,如图5所示。由图5可知,数值模拟得到的结果略大于实验结果,但总体误差约为10%,且两者变化趋势一致,验证了模型的正确性。

2 结果与分析

2.1 不同结构对温度场和速度场的影响

2.1.1 温度场分析

图7 局部及纵截面温度分布云图

由图7的局部和纵截面温度分布云图可知,改进结构后翅片周围空气域的平均温度有不同程度的提高,其中case 1～case 3的纵截面平均温度分别为332.518、332.289、331.619 K,与传统锯齿翅片相比分别提高5.787、5.558、4.888 K,说明有更多的热量从热翅片传递至冷空气而被其带走。分析原因是改进结构后翅片壁面附近的热边界层较传统锯齿翅片更薄,热阻减小,更利于对流传热,且在材料质量不变的情况下,改进后的翅片比传统锯齿型翅片的散热面积有所增加。同时,无论是何种形状,冷空气与热翅片在凹槽位置会比凸起位置传递更多热量,分析原因是冷空气在凹槽的位置会短暂积聚,与热翅片接触的时间相对更长,且扰动更剧烈,所以热传递带走的热量更多。

2.1.2 速度场分析

速度场如图8和图9所示。由图8横截面速度分布云图可知,4种翅片均在主流道流速较快,翅片表面附近的流速较低。与传统锯齿翅片相比,改进结构后平均风速会提高,其中case 0～case 3的横截面平均速度分别为2.363、2.395、2.396、2.391 m/s,3种形状对横截面平均速度提高的影响程度相差较小。

图8 横截面速度分布云图

图9 局部及纵截面速度分布云图

由图9局部和纵截面速度分布云图可知,改进结构后翅片周围空气域的平均速度有不同程度的提高,其中case 0～case 3的纵截面平均速度为2.389、2.436、2.435、2.429 m/s,矩形和圆形几乎相同,三角形提高最少。同时,改进后的翅片比传统锯齿型翅片整体速度边界层更薄,但在凹槽位置的速度边界层会变厚,原因是空气在沿翅片表面流动时,由于凸起和凹槽的存在,会产生背向凸起和流向凹槽的分速度,整体流速不再平行均匀流动,在凹槽位置由于产生流向槽内的空气,所以槽内空气停留时间更长,与温度分布规律相对应。

2.2 不同结构对翅片综合性能的影响

为更加完整地揭示三维模型整体的传热性能,以凹槽和凸起高度R=0.1 mm 时的数值模拟结果为例对散热单元的综合性能进行分析。通过改变结构会使Nu提高的同时伴有Δp的损失,因此评价其综合性能时需要同时考虑散热和压降两方面因素,以η作为评价散热器综合性能的指标。

不同形状对Nu、Δp、η的影响如图10和图11所示。由图10(a)可知,无论是何种形状,改进后翅片的Nu均高于传统锯齿型翅片,且两者之间的差值随Re的提高而增大,与传统锯齿型翅片相比,改进后的翅片Nu平均提高了9.4%。同时,改进时所选形状对Nu提高的影响程度几乎无差异。由图10(b)可知,与Nu影响规律类似,无论是何种形状,改进后翅片的Δp均高于传统锯齿型翅片,且两者之间的差值随Re的提高而增大。但改进时所选形状对Δp的影响效果与Nu不同,矩形和三角形对Δp的影响差异较小,且影响程度几乎不随Re的改变而改变,圆形的压降小于前两者,且差值随Re的提高而增大,因此改进时考虑压降因素应选压降损失更小的圆形。

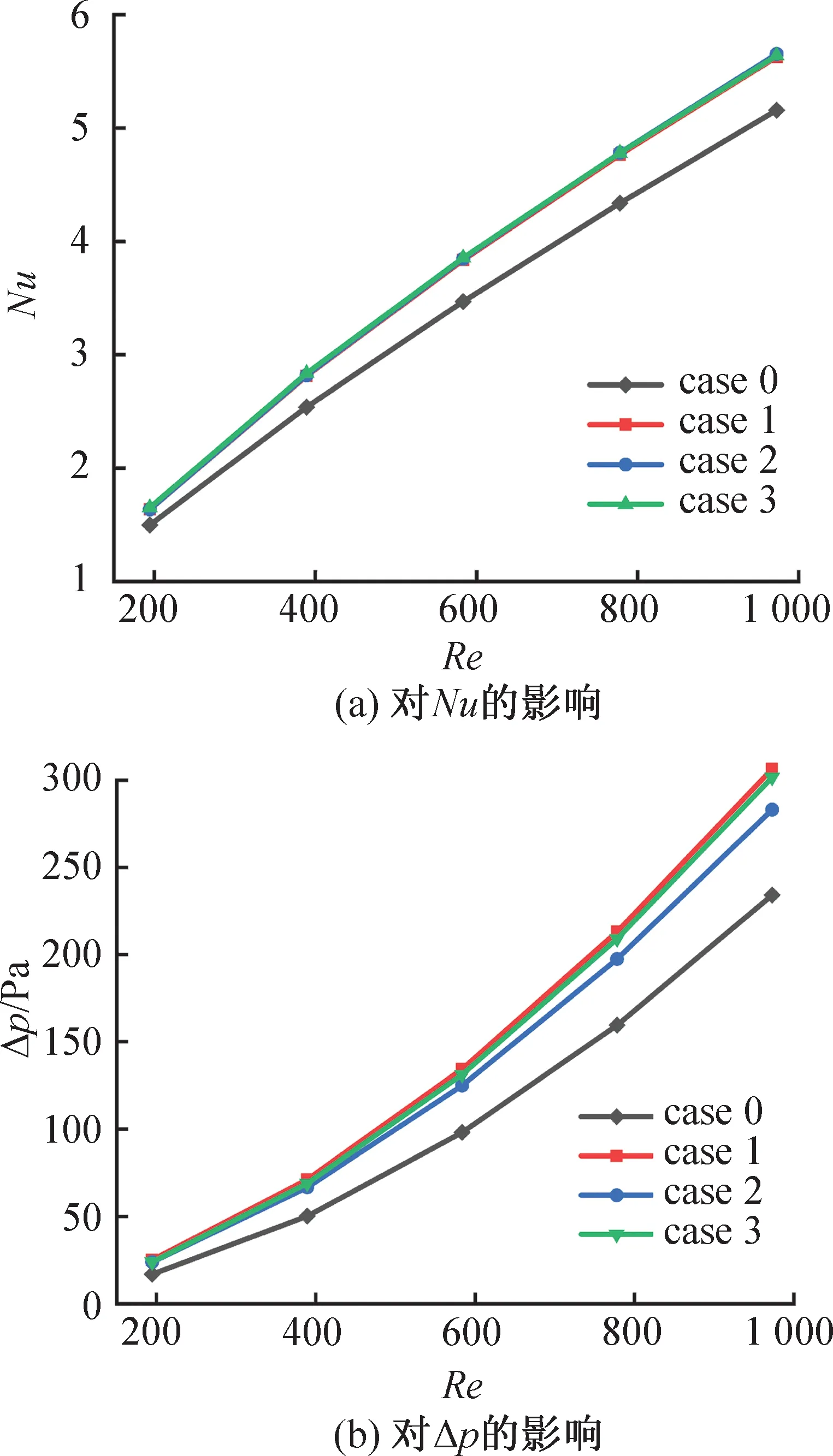
图10 不同形状对性能的影响

图11 不同形状对综合性能η的影响

由图11可知,无论何种形状,改进后翅片的综合性能评价指标η与Re均呈正相关,但随Re的提高,圆形较矩形和三角形的差值均增大,三角形较矩形之间的差值减小。圆形的综合性能优于另外两种,因此在翅片表面设置凹槽和凸起时选择形状为圆形。

在综合考虑散热和压降的情况下,在翅片表面设置圆形凹槽和凸起时,当Re<300时,综合性能评价指标η<1,说明虽然改进后的翅片散热性能有所提高,但也损失了过多的压降,导致综合性能下降,因此在圆形case 2的基础上将翅片两端也改进为圆形成为case 4。

改进翅片两端结构对Nu、Δp、η的影响如图12和图13所示。由图12可知,相较于传统锯齿型翅片,改进后的case 4的Nu平均提高7%。同时,当Re>400时,压降损失反而减小,且随Re的提高压降损失的差值增大,Re=972.5时压降损失最大减小了21%。由图13可知,在case 2 的基础上继续改进翅片两端的结构后,散热翅片的η均大于1,最高提高了12.2%,说明改进后的最终结构在提高散热的同时也有效缓解了压降损失。

图12 改进翅片两端结构对Nu和Δp的影响

图13 改进翅片两端结构对η的影响

2.3 不同参数对翅片综合换热性能的影响

以翅片结构为case 4时为例对散热单元进行数值模拟,分析圆形凹槽和凸起高度R对强化传热性能的影响。不同凹槽和凸起高度对Nu、Δp、η的影响如图14和图15所示。由图14(a)可知,在相同Re条件下,随着R的增大,Nu也增大,散热性能增强,但从R=0.05 mm至R=0.20 mm每次高度增加0.05 mm 的过程中Nu的增长趋势减缓,强化传热程度减弱。由图14(b)可知,圆形凹槽和凸起高度R对压力损失Δp的影响规律与Nu类似,在相同Re条件下,高度R与压降损失Δp呈正相关。同时,当R<0.15 mm时,相较于传统锯齿型翅片,改进后的平均压降损失反而减小,当R≥0.15 mm时,平均压降损失与传统锯齿型翅片基本持平。

图14 不同凹槽和凸起高度对性能的影响

图15 不同凹槽和凸起高度对η的影响

由图15可知,随着圆形凹槽和凸起高度R的增加,综合性能η也相应增大,R=0.05 mm时综合性能平均提高11.2%,R=0.20 mm时综合性能平均提高6.8%。分析原因,当Re=583.5时,相较于传统锯齿型翅片,改进后R=0.05 mm时Nu仅提高了3.1%,而Δp减小了8.4%,由η的定义及图14可知,R=0.05 mm时η最大的原因是Nu小幅增大的同时Δp却大幅减小。而改进后R=0.20 mm时Nu提高10.5%,而Δp仅增加2.1%,R=0.20 mm时η最小的原因是Nu大幅增大的同时Δp也小幅增大。因此应选取合适的高度来达到Nu和η的平衡,R=0.15 mm时,与传统锯齿型翅片相比,平均压降损失Δp基本不变,而Nu平均提高8.7%,η平均也提高8.7%。