制冷换热器双侧强化换热管的实验方法对比

苏博文 欧阳新萍

(上海理工大学能源与动力工程学院 上海 200093)

管壳式换热器结构简单、适用性强[1],常用于大型制冷系统中[2],其性能的改善可节约成本和能源[3]。双侧表面强化换热管,采用特定表面结构以增加传热面积和提升换热效果[4],被广泛用于制冷管壳式换热器。对于强化管的性能测试,由于其表面结构复杂,不便在壁面布置温度传感元件,故管内或管外的传热性能很难直接检测。因此,一般通过检测总传热系数,再通过合适的实验和数据处理方法来获得管内、管外对流换热表面传热系数。这些方法包括Wilson图解法(Wilson plot method, WPM)[5]和Gnielinski公式[6]。WPM是分析管壳式换热器中换热管对流换热表面传热系数的优质工具[7],优于经典热阻法[8]。此外WPM可用于拟合圆管中的不同流态下的换热关联式[9]以及确定复杂情况下的对流换热表面传热系数[10]。然而,在分析整体传热数据时,很难评估WPM获得结果的准确性[11]。许多学者使用Gnielinski公式[6]进行研究,该公式能够预测90%以上的实验数据,准确率在±15%以内[12],计算不同类型强化管对流换热表面传热系数的误差较小[13-14]。

WPM和Gnielinski公式适用于管内光滑管, 对于双侧强化管,需要对其进行修正和变型。如通过修正Copper和Wojtan公式拟合强化管管内沸腾的传热系数[15]、修正Gnielinski公式[16](modified Gnielinski formula, MGF)、WPM与Gnielinski公式一起使用的Wilson-Gnielinski公式[17](Wilson-Gnielinski formula, W-GF)等。通过修正和变型,MGF和W-GF提高了计算强化管对流换热表面传热系数的精确性。冀文涛等[16]使用MGF分析不同强化管,93%数据偏差在±20%以内。W-GF可用于分析强化管性能[18],且平均标准误差较小[19],可靠性较高[20]。这两种方法可以避免WPM中要求的“Re的指数为定值”的限制,但其分别引入流动阻力系数和强化倍率的假定,在数据处理过程中会产生误差。

此外,上述研究一般针对某种实验和数据处理方法进行分析,很少在不同方法之间进行对比。本文对一种双侧强化管的传热性能进行了实验,提出了一种高效分离管内、管外对流换热表面传热系数的实验方法,称为待定指数法(undetermined exponent method,UEM)。在实验数据处理中,将UEM与WPM、MGF和W-GF进行应用对比。

1 制冷换热器双侧强化管实验方法

通过实验测得的温度和流量数据可计算换热量Q以及对数平均温差ΔTLMTD,总传热系数K[W/(m2·K)]计算如下:

Ao=πdoL

(1)

(2)

式中:Ao为蒸发管外名义表面积,m2;do为蒸发管光滑段外径,m;L为蒸发管光滑段长度,m;Q为换热量,W;ΔTLMTD为对数平均温差,K。

总传热系数与管内、外对流换热表面传热系数关系如下:

(3)

式中:hi、ho分别为强化管管内、管外对流换热表面传热系数,W/(m2·K);Rw、Rf分别为管壁导热热阻、管内污垢热阻,(m2·K)/W;di为蒸发管光滑段内径,m。

1.1 Wilson图解法(WPM)

Wilson图解法是经典的管内、管外对流换热表面传热系数实验测试方法。要求在若干个工况的实验中,保持换热壁面某一侧的对流换热表面传热系数不变,改变另一侧的流体流速,从而得到两侧的对流换热表面传热系数。前提条件:变流速一侧对流换热表面传热系数与流速的幂次关系必须已知。该方法的更多细节可参见文献[5]。对于管内表面,对流换热表面传热系数计算如下:

(4)

(5)

Y=1/K

(6)

式中:ci为系数;ui为管内流体流速,m/s;X、Y均为系数。

对式(3)进行线性拟合得到常数ci, 进而计算得到hi和ho。对于双侧强化管,流速幂指数非0.8,而是依据表面结构确定,所以该方法不适用。若仍假定强化管hi计算式中流速的指数为0.8,则会带来一定误差。

1.2 修正Gnielinski公式法(MGF)

Gnielinski公式用于光滑管管内的对流换热表面传热系数计算。对于强化管,将Gnielinski公式分子中光滑管阻力系数f替换为强化管阻力系数fr[16],即:

(7)

(8)

式中:Nu为流体的努塞尔数;Δp为强化管流动阻力损失,Pa;ρ为流体密度,kg/m3;Re为流体的雷诺数;Pr为流体的普朗特数;下标w为壁面;根据式(7)结果计算强化管hi:

hi=Nuλ/di

(9)

式中:λ为导热系数,W/(m·K)。通过式(3)分离出ho。MGF无需知道WPM中所要求的流速的幂指数,但需知道或测定强化管内的阻力系数fr,且式(7)的理论依据不足。

1.3 Wilson-Gnielinski公式法 (W-GF)

强化管的hi可认为是光滑管管内对流换热表面传热系数hip(W/(m2·K))的βi倍[17],称βi为强化管管内对流换热表面传热系数的强化倍率,即:

hi=βihip

(10)

将式(10)代入式(3),实验过程中ho保持不变,仅改变管内流速,令:

(11)

(12)

式中:a、b均为系数。以1/hip为自变量、1/K为因变量,根据实验数据进行线性拟合,得到a、b数值,即可分离得到hi和ho。

与MGF相比,W-GF除了避免“流速或Re的指数需已知”的条件,还无需测量或计算fr,更便于应用。式(10)中假定βi为定值,实际的βi会随管内Re变化而变化,因此会导致一定的误差。

1.4 待定指数法(UEM)

UEM是本文提出的应用于双侧强化管实验的新方法。Sieder-Tate[21]公式常用于光滑管内湍流对流换热表面传热系数的计算。而对于强化管,固定的系数和指数不再适用,而是与强化表面结构相关的待定值。因此,管内对流换热表面传热系数的计算可修改如下:

(13)

(14)

式中:Ci、C′i为系数;n为指数。将式(14)代入式(13)中,再将化简后的公式代入式(3),可得:

(15)

实验过程中ho保持不变,仅改变管内流速,令:

(16)

X=1/Ren

(17)

式中:ε为系数。同时将式(6)和式(12)代入,则式(15)可表示为:

Y=εX+b

(18)

通过实验的各工况获得Rej和Kj的值。先假设一个n的初值,可得:

(19)

Yj=1/Kj

(20)

再根据式(18)拟合得到ε、b的初值。以ε、b、n的初值通过式(18)计算各工况的K′j值。建立目标函数Z:

Z=(K1-K′1)2+(K2-K′2)2+…+

(Kj-K′j)2+…+(KN-K′N)2

(21)

式中:Kj(j=1,2,3,…,N)为总传热系数的实验值;K′j为根据式(18)计算的理论值;N为测试点或测试条件的数量。不断调整n的数值,直至目标函数Z的数值达到最小,即认为此时的n值为最优值,相应的ε、b值也为最终所求值。

经验表明,n值通常在[0.3,1]区间内,可以使用0.618寻优法在该区间内找到使函数Z最小化的最佳n值。然后获得ε和b的相应最佳值,从而计算出合理的管内、外对流换热表面传热系数。

综上所述,UEM方法无需知道强化管内对流换热表面传热系数的相关公式中流速的指数以及管内的阻力系数,也无需式(10)的近似假设,因此UEM比上述3种方法更容易应用。无假设条件,因此也更准确。

2 双侧强化管实验台及实验结果

2.1 实验管与实验台

实验用双侧强化管如图1所示,结构参数如表1所示。实验管长为3.2 m,是由两个1.6 m长的紫铜(T2)实验管串联而成。管内和管外的流体分别为水和制冷剂R134a。

表1 双侧强化管结构参数

图1 双侧强化管理论截面和实际截面

实验台如图2所示,实验管放置在蒸发筒体内,进行管外满液式蒸发实验。有3个主要回路:实验管外的制冷剂(R134a)回路、管内的水回路、冷凝器管内的乙二醇回路。还有两个带有制冷装置的辅助回路,每个回路分别提供实验要求温度的乙二醇溶液和水。

图2 实验装置

2.2 不确定度

根据测量不确定度指南[22]进行计算,各种方法的不确定度结果在后续相关图中给出了范围标示。

2.3 实验结果

第一组工况中,蒸发压力为0.357 MPa(对应5.6 ℃的饱和蒸发温度),蒸发管的热通量q为40 kW/m2,此时ho可基本保持不变。水流速ui在1.0～3.0 m/s之间变化,共测试7个工况,测试结果如图3所示。该组数据可采用前述各种实验方法分离得到hi。

图3 管内变流速工况

第二组工况中,ui保持 3.0 m/s,蒸发压力仍控制在0.357 MPa,热通量q在15～46 kW/m2之间变化,共7个工况,实验结果如图4所示。该组数据用于得到ho的规律。

图4 管外变热流工况

3 数据处理结果和对比

根据第一组工况中的数据,分别使用上述4种实验方法来分离强化管管内、外对流换热表面传热系数。

3.1 不同实验方法得出hi的数据结果

3.1.1 Wilson图解法 (WPM)

假定强化管管内对流换热计算式中流速的指数为0.8,根据WPM,威尔逊图如图5所示,拟合数据如下:

图5 WPM的威尔逊图

(22)

将hi代入式(3),可计算得到ho。为得出强化管管内对流换热表面传热系数的强化倍率,光滑管管内对流换热表面传热系数采用经典Sieder-Tate[21]公式进行计算:

(23)

式中:μfl、μw分别为以流体平均温度、壁面温度为定性温度的动力粘度,Pa·s。

(24)

将各参数代入,得ci为0.085,式(22)变型为:

(25)

通过式(10)计算强化管管内对流换热表面传热系数的强化倍率βi为3.15。

3.1.2 修正Gnielinski公式法(MGF)

图6、图7所示分别为fr、hi与Re的关系。采用前述MGF方法,计算得:

图6 流动阻力fr和Re的关系

图7 MGF中Re和hi的关系

hi=5.506Re0.782

(26)

准则式形式为:

(27)

由于Re的指数与光滑管不同,计算强化管管内对流换热表面传热系数的强化倍率时需选择比较基准。选择Re为27 000作为基准,得βi为3.23。

3.1.3 Wilson-Gnielinski公式法(W-GF)

如图8所示,通过Wilson-Gnielinski图拟合出斜率a为0.376 2后,得强化管管内对流换热表面传热系数的强化倍率βi为2.92。hi和Re之间的关系如图9所示,通过幂函数对图9中的数据拟合可得:

图8 Wilson-Gnielinski图

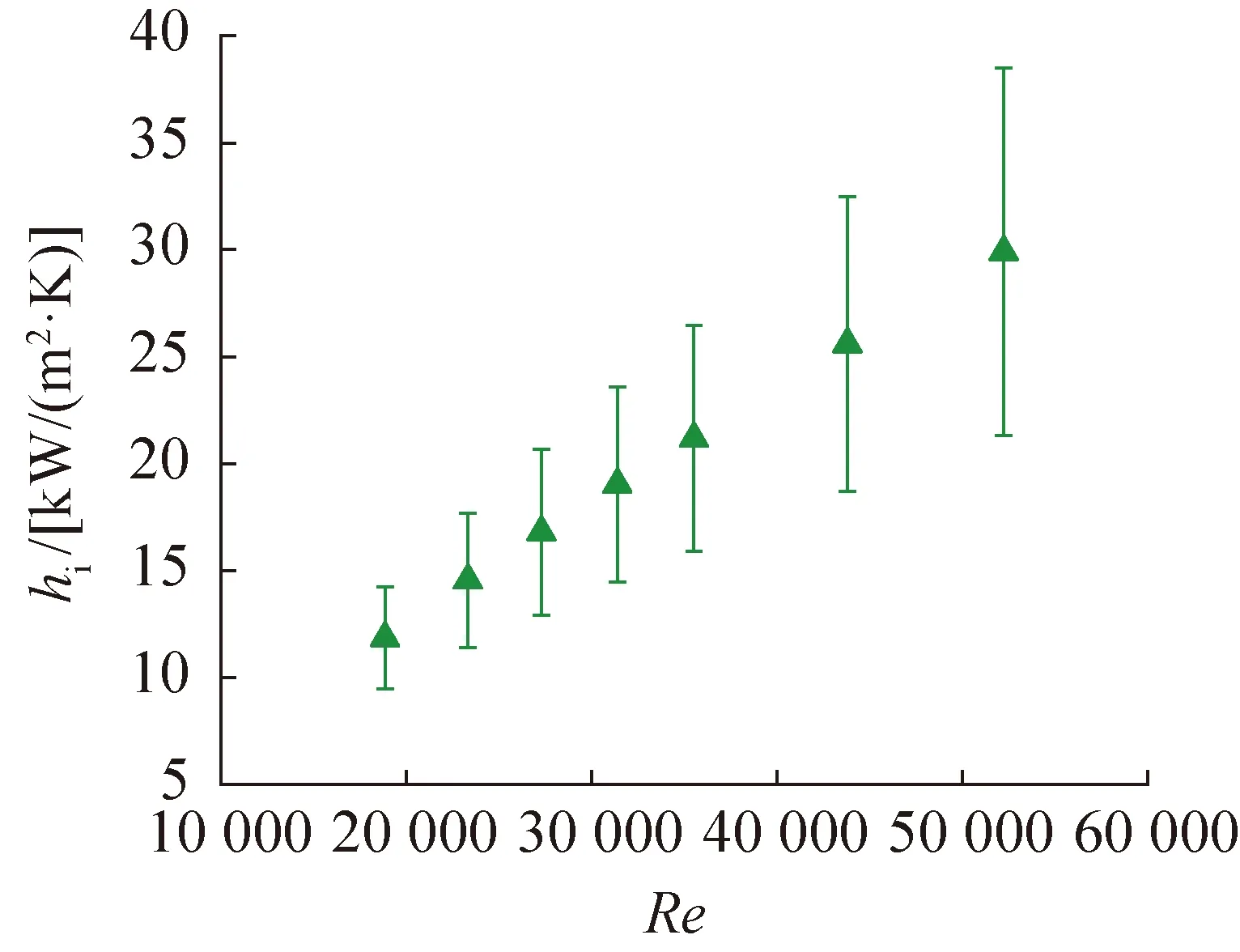
图9 W-GF中Re和hi的关系

hi=1.629Re0.904

(28)

再根据式(23)的准则关联式整理得到:

(29)

3.1.4 待定指数法(UEM)

采用前述UEM方法,计算得到最佳n为0.796,ε和b的值分别为0.000 05和0.252 7,则:

(30)

hi=4.34Re0.796

(31)

整理得准则关联式:

(32)

hi和Re之间的关系如图10所示,强化管管内对流换热表面传热系数的强化倍率βi为2.88。

图10 UEM中Re和hi的关系

3.2 管内对流换热表面传热系数hi对比

对于不同方法得出的hi对比如图11所示。当管内Re低于27 000时,不同方法得出的hi差异较小,而随着水流速度的增加,差异逐渐增大。W-GF的hi高于其他方法,而UEM低于其他方法。在实验的最低Re(约19 000) 时,4种方法得到的hi的不确定度范围在18.8%～20.2%之间,在最高Re(约52 000)时,不确定度范围稍大,在11.0%～28.7%之间。其中,UEM的不确定度最小,在上述Re范围时为18.8%～11.0%。在不同方法下,由WPM、MGF、W-GF和UEM给出的βi分别为3.15、3.23、2.92和2.88,不同方法之间的βi差异在1.5%～15.0%之间,这也是4种方法得到的hi的差异范围。

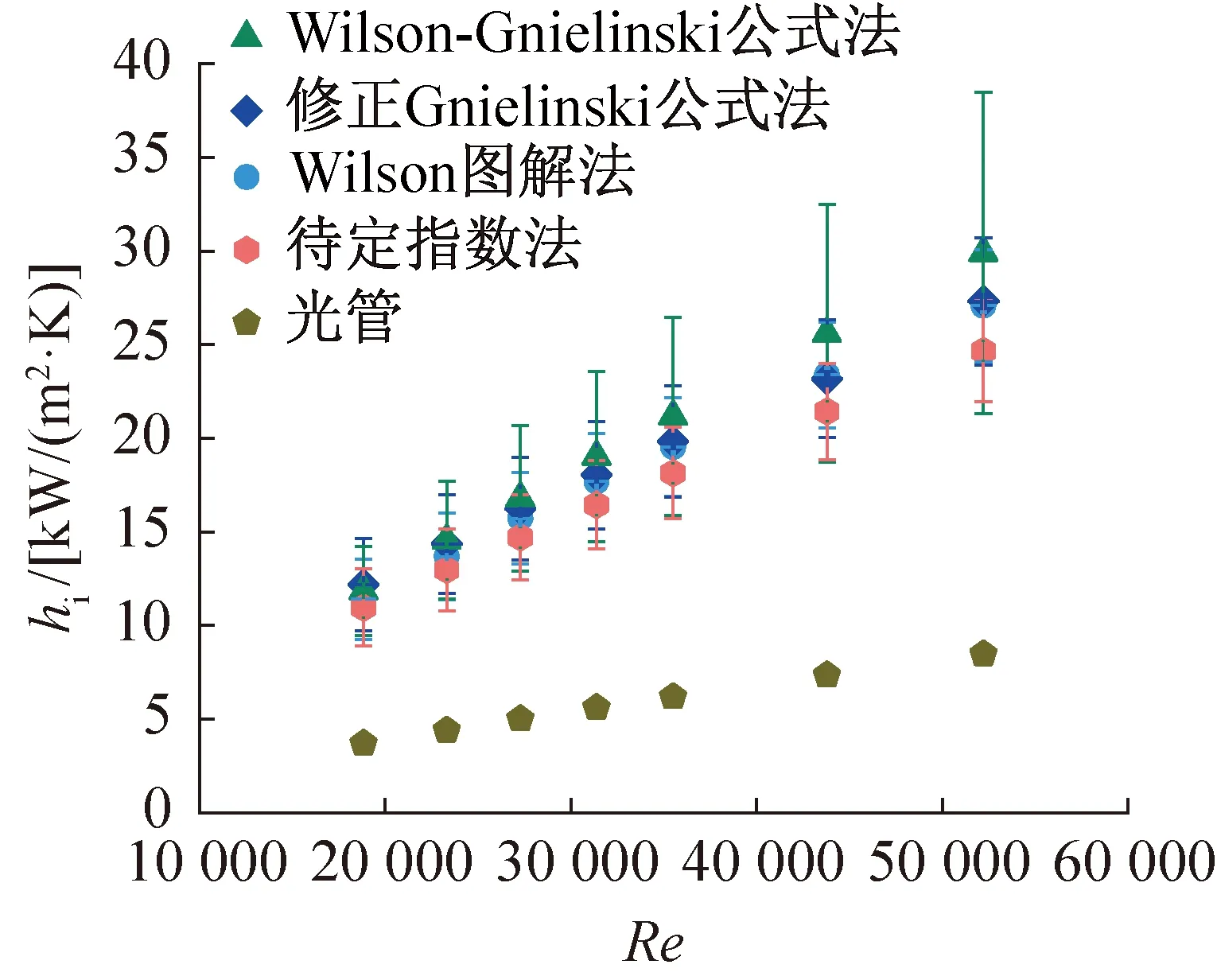
图11 不同实验方法下hi对比

3.3 管外对流换热表面传热系数ho对比

基于第二组工况中的数据,通过3.1中的计算方法获得不同实验方法对应的hi,再通过分离得到不同实验方法下ho。不同实验方法下ho随q的变化如图12所示。使用Copper公式[23-24]计算光滑管的管外对流换热表面传热系数hop[W/(m2·K)]。

图12 不同实验方法下ho随q的变化

hop=Cq0.67Mr-0.5prM(-logpr)-0.55

(33)

M=0.12-0.2logRp

(34)

式中:C为Copper系数,取值为90;Mr为液体的分子量;M为系数;pr为对比压力,其值等于液体实测压力与临界压力之比(管外制冷剂为R134a,临界压力为4.07 MPa);Rp为平均表面粗糙度,μm,对于被测管Rp取0.35 μm。

通过幂函数拟合图12中的数据,得出管外蒸发的传热关联式:

WPM:ho=208.2q0.426

(35)

MGF:ho=221q0.418

(36)

W-GF:ho=245.4q0.405

(37)

UEM:ho=162.2q0.457

(38)

与光滑管相比,WPM、MGF、W-GF和UEM得出的管外对流换热表面传热系数的强化倍率βo分别为3.30、3.24、3.15和3.54。4种方法所得结果之间存在差异,差异范围为1.8%～11.0%,这也是4种方法得到的ho的差异范围。

从4种方法得到的强化管管内、管外对流换热表面传热系数差异较小,4种方法均可用于双面强化管的性能实验,但前3种方法均存在各自的应用局限性和应用误差,应根据具体的已知条件、应用条件选择使用。UEM应用限制条件少、使用方便、误差较小,推荐使用。分析大量文献报道的数据,认为该方法所得的管内强化倍率为2.88、管外强化倍率为3.54的数据更可靠。

4 结论

本文使用4种实验方法对双侧强化换热管进行满液式蒸发换热实验并进行数据处理。得到结论如下:

1)4种方法获得的管内、管外对流换热表面传热系数的偏差分别在15%、11%之内,差异较小,因此均可作为双侧强化管的性能实验方法。但WPM、MGF、W-GF方法均存在各自的应用局限性和应用误差,所以应根据具体的已知条件、应用条件选择使用。UEM方法应用限制条件少、使用方便、误差较小,用于双侧强化管的换热性能测试更合适。

2)4种实验方法得到的强化管管内、管外对流换热表面传热系数强化倍率范围分别为2.88～3.23、3.15～3.54。UEM方法所得的管内、管外对流换热表面传热系数强化倍率分别为2.88、3.54,数据更可靠。