求数列通项公式的新视角——构造常数列

赵世瑜

(甘肃省渭源县第一中学,甘肃 定西 748200)

在等差数列、等比数列以外的一些特殊数列中,我们常用累加法、累积法和构造法求其通项公式,这些方法都对应某种特定的类型,运用起来程序性强,学生很容易掌握.笔者经过研究,发现此类问题可以通过构造常数列加以解决,现将自己的一些心得整理出来,希望能起到抛砖引玉的作用.

1 常数列的定义

如果数列{an}满足an+1=an,则称{an}为常数列,此时有an=a1.

2 构造常数列求通项公式

2.1 an+1=an+f(n)型

例2 在数列{an}中,a1=1,an-an-1=2n-3,n≥2,n∈N*,求{an}的通项公式.

解因为an-an-1=2n-3,所以an-(n-1)2=an-1-(n-2)2,n≥2,n∈N*,所以数列{an-(n-1)2}是一个常数列.

又因为首项为a1-(1-1)2=1,所以an=(n-1)2+1=n2-2n+2,n∈N*.

例3已知数列{an}满足an+1-an=4n+1,且a1=1 求数列{an}的通项公式.

解因为an+1-an=4n+1,所以an-an-1=4n-3,n≥2,n∈N*.

所以an-(2n2-n-1)=an-1-[2(n-1)2-(n-1)-1],n≥2,n∈N*,所以数列{an-(2n2-n-1)}是一个常数列.

又因为首项为a1-(2×12-1-1)=1,所以an=2n2-n,n∈N*.

评注我们可以感受到此方法在语言表达上比用累加法显得更加简洁,同时肯定有人看完例2,3会感慨:此法只应天上有!其实不然,下面给出一般性的结论.

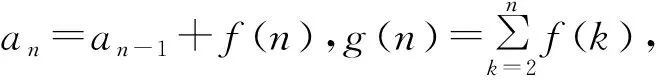
也许有读者会问:g(n)是怎样构造出来的呢?方法如下:

假设an-g(n)=an-1-g(n-1),则g(n)-g(n-1)=f(n),所以g(2)-g(1)=f(2),g(3)-g(2)=f(3),…,g(n)-g(n-1)=f(n),n≥2,n∈N*.

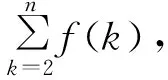
2.2 an+1=anf(n)型

例4 在数列{an}中,a1=1,an+1=2nan(n∈N*),求通项an.

类似地,我们可以得到以下结论.

g(n)的构造方法如下:

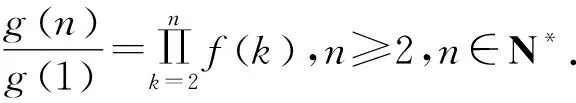
2.3 an+2=(1-λ)an+1+λan型

例5 已知数列{an}满足:a1=2,a2=3,an+2=3an+1-2an(n∈N*),求数列{an}的通项公式.

解因为an+2=3an+1-2an(n∈N*),所以an+2-2an+1=an+1-2an(n∈N*),所以数列{an+1-2an}是以a2-2a1=-1为首项的常数列,即an+1-2an=-1,从而an+1-1=2(an-1).

又因为a1-1=1,所以{an-1}是以1为首项,2为公比的等比数列,所以an-1=2n-1,即an=2n-1+1(n∈N*).

我们可以把以上问题推广到一般情景.

定理3数列{an}满足:a1=a,a2=b,an+2=pan+1+qan(n∈N*,p2+4q≥0),

即x2=px+q,解得x=α或x=β,其中α+β=p,αβ=-q.

由①得an+1-αan=(b-αa)βn-1,

③

由②得an+1-βan=(b-βa)αn-1,

④

3 在高考中的应用

例6(2012年大纲全国卷)[1]函数f(x)=x2-2x-3.定义数列{xn}如下:x1=2,xn+1是过两点P(4,5),Qn(xn,f(xn))的直线PQn与x轴交点的横坐标.

(1)证明:2≤xn

(2)求数列{xn}的通向公式.

解(1)略.

例7(2008年四川卷理科)设数列数列{an}的前n项的和为Sn,已知ban-2n=(b-1)Sn.

(1)证明:当b=2时,{an-n·2n-1};

(2)数列{an}的通向公式.

解(1)略.(2)当b=2时,由(1)知,an=(n+1)2n+1.当b=0时,则an=2n-1;

该法在中学数学教学中2012年大纲全国卷[1]等有运用,我们的老师不仅要把解题技巧传授给学生,更重要的是要教会学生思考问题、教会学生领悟数学的思想方法,从而理解数学的本质.因为思维是数学的灵魂,技巧是灵活的,但思想方法却可以举一反三. 我们可用常数控制变数,通过构造常数列来求解数列的通项公式[2].