P3C-MADDPG算法的多无人机协同追捕对抗策略研究

高甲博 肖玮 何智杰

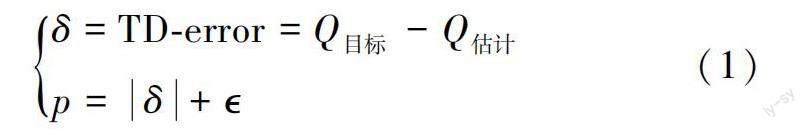
摘 要：針对策略未知逃逸无人机环境中多无人机协同追捕对抗任务，提出P3C-MADDPG算法的多无人机协同追捕对抗策略。首先，为解决多智能体深度确定性策略梯度（Multi-Agent Deep Deterministic Policy Gradient，MADDPG）算法训练速度慢和Q值高估问题，在MADDPG算法中分别采用基于树形结构储存的优先经验回放机制（Prioritized Experience Replay，PER）和设计的3线程并行Critic网络模型，提出P3C-MADDPG算法。然后基于构建的无人机运动学模型，设计追逃无人机的状态空间、稀疏奖励与引导式奖励相结合的奖励函数、加速度不同的追逃动作空间等训练要素。最后基于上述训练要素，通过P3C-MADDPG算法生成策略未知逃逸无人机环境中多无人机协同追捕对抗策略。仿真实验表明，P3C-MADDPG算法在训练速度上平均提升了11.7%，Q值平均降低6.06%，生成的多无人机协同追捕对抗策略能有效避开障碍物，能实现对策略未知逃逸无人机的智能追捕。

关键词：P3C-MADDPG；协同追捕对抗策略；优先经验回放；Q值；多无人机

中图分类号：E911文献标志码：ADOI：10.3969/j.issn.1673-3819.2023.06.002

Research on multi-UAV cooperative pursuit and confrontation

strategy based on P3C-MADDPG algorithm

GAO Jiabo^1，2， XIAO Wei¹， HE Zhijie^1，3

（1. Army Logistics Academy，Military Logistics Department，Chongqing 400000， China; 2. Unit 95019 of the Peoples

Liberation Army，Xiangyang 441100， China; 3. Unit 31680 of the Peoples Liberation Army， Chongzhou 611230，China）

Abstract：Aiming at the cooperative pursuit and confrontation task of multiple UAVs in the unknown escape UAV environment， a multi-UAVs cooperative pursuit and confrontation strategy based on P3C-MADDPG algorithm is proposed. First， in order to solve the problem of slow training speed and over estimation of Q value of Multi-Agent Deep Deterministic Policy Gradient （MADDPG） algorithm， In MADDPG algorithm， Prioritized Experience Replay （PER） based on tree structure storage and a parallel Critic network model with 3 threads are prioritized respectively， and the P3C-MADDPG algorithm is proposed. Then， based on the kinematics model of UAV， training elements such as state space， reward function combining sparse reward and guided reward， pursuit action space with different accelerations are designed. Finally， based on the above training elements， the P3C-MADDPG algorithm is used to generate the cooperative pursuit and confrontation strategy of multiple UAVs in the unknown escape UAV environment. Simulation experiments show that the P3C-MADDPG algorithm increases the training speed by 11.7% on average， and decreases the Q value by 6.06% on average. The generated multi-UAV cooperative pursuit and confrontation strategy can effectively avoid obstacles， and more intelligently realize the pursuit of unmanned aerial vehicles with unknown strategies.

Key words：P3C-MADDPG; coordinated pursuit and confrontation strategy;prioritized experience replay; Q value; multi-UAVs

收稿日期：2023-07-06

修回日期：2023-08-08

*基金项目：重庆市教委科学技术研究项目基金（KJZD-K202312903）;陆军勤务学院研究生科研创新项目基金（LQ-ZD-202209）;陆军勤务学院科研项目（LQ-ZD-202316）;重庆市研究生科研创新项目（CYS23778）

作者简介：

高甲博（1995—），男，硕士研究生，研究方向为无人机集群控制。

通信作者：肖 玮（1982—），女，副教授，博士。

现代战争中，无人机被大量投入战场，发挥成本低、灵活性强、冗余抗损等优势，迅速成为影响战争态势发展的关键力量^[1]。多无人机协同追捕对抗任务是无人机在现代战争中的典型应用^[2-6]，其实质是多智能体智能决策问题。学术界中应用较多的基于数学模型和仿生的多无人机协同追捕对抗策略，往往需要已知逃逸无人机策略。如文献[7]和[8]分别采用Voronoi图和阿波罗尼奥斯圆理论方法解决多智能体协同追捕问题。文献[9]和[10]分别提出仿鹰-欧椋鸟和仿灰狼智能行为和团队合作行为，给出了无人机集群追逃控制方法。真实战场环境中逃逸无人机的策略往往未知，因此对于策略未知逃逸无人机环境中多无人机协同追捕对抗任务研究更具重要意义和实用价值。

多智能体强化学习（Multi-Agent Reinforcement Learning，MARL）^[11]具有对未知环境学习探索的特点。随着MARL的广泛应用，将其用于解决多无人机协同追捕对抗策略问题，是实现空战智能决策的重要技术范式^[12]。文献[13]针对太空中多智能体之间的追逃博弈问题，应用MARL中的多智能体深度确定性策略梯度（Multi-Agent Deep Deterministic Policy Gradient，MADDPG）算法对智能体运动策略进行训练，使其涌现出“围捕”“拦截”“合作”“潜伏”等系列智能博弈行为。文献[14]将合作博弈中的凸博弈与非合作博弈中的马尔科夫博弈相结合，提出用马尔科夫凸博弈来解决智能体的协同对抗问题。文献[15]在基于MARL中的深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG）算法基础上，通过由易到难的课程学习方式不断提高无人机追捕能力，有效提高了算法的泛化性。

MARL系列算法是基于探索学习的，通过多次训练在一定程度上能实现对策略未知逃逸无人机的追捕。但由于经常采样到价值较低的经验数据，导致MARL系列算法训练速度慢。且由于以最大Q值作为期望Q值，使得Q值出现高估问题，导致策略网络训练迭代目标不准确，影响生成策略的智能性。为此，文献[16]从经验回放池数据着手，将并行、优先经验回放的思想融入MADDPG算法中，采用[M/N]个线程对经验池数据并行处理，选择损失函数值最小的线程网络梯度参数更新主网络梯度参数，在相同时间内使得经验数据的吞吐量扩展至[M/N]倍，从而提升训练速度。文献[17]将优先经验回放（Prioritized Experience Replay，PER）机制与传统深度强化学习算法和匈牙利算法相结合，提高高价值经验数据的利用率，加快算法收敛速度。文献[18]为解决深度Q网络（Deep Q-Network，DQN）算法Q值高估的问题，对目标网络和当前网络独立地进行价值估计，将最优动作选择和价值评估分开进行，一定程度解决Q值高估带来的影响。文献[19]通过选取双Critic网络中较小的估计Q值计算损失，相较于MADDPG算法有了更好效果。上述研究和改进大多应用在较为理想的任务环境，对于策略未知逃逸无人机等环境中多无人机协同追捕对抗任务研究较少。

针对上述问题，本文开展存在策略未知逃逸无人机环境中多无人机协同追捕对抗任务研究。首先为提高训练速度，加快算法收敛，采用基于树形结构储存的PER机制^[20-21]对MADDPG算法随机采样过程进行改进。为解决MADDPG算法存在Q值高估问题^[22]，设計3线程并行Critic网络模型，提出P3C-MADDPG（P—PER，3C—3线程并行Critic网络模型）算法。然后基于构建的无人机运动学模型，设计追逃无人机的状态空间、稀疏奖励与引导式奖励相结合的奖励函数、加速度不同的追逃动作空间等训练要素。最后基于上述训练要素，通过P3C-MADDPG算法生成策略未知逃逸无人机环境中多无人机协同追捕对抗策略。

1 P3C-MADDPG算法

1.1 P3C-MADDPG算法原理

P3C-MADDPG算法原理如图1所示。首先，进行马尔科夫博弈（Markov game）^[23]。各智能体依据当前t时刻的环境状态S_t，通过Actor网络选取动作A_t并执行，各智能体获得奖励R_t并进入下一状态S_t+1，产生以D=（S_t，A_t，R_t，S_t+1）为一组的训练数据。

其次，设计基于树形结构储存的优先经验回放机制（PER）。每组训练数据及其优先级（D，p）存入树形结构经验池的叶子中作为经验数据。当经验池中储存的经验数据量达到池子一半大小时，依据采样概率，采样m组优质经验数据。同时计算经验数据的重要性采样权重，用于修正经验数据分布。

再次，设计3线程并行Critic网络模型。该模型由3个相同的Critic评价网络并行组成，通过3个Critic评价网络同时对Q值进行估计。

最后，使用采样的经验数据对每个智能体的Actor网络和3线程并行Critic网络模型进行训练。当每局平均收益奖励值变化低于某阈值时，说明算法训练达到收敛状态，此时智能体的Actor网络和3线程并行Critic网络参数实现稳定。

1.2 P3C-MADDPG算法关键技术

1.2.1 基于树形结构储存的优先经验回放机制

MADDPG算法经常采集到大量价值很小的经验数据用于对网络模型进行训练，导致算法训练过慢。为此，在P3C-MADDPG算法中设计基于树形结构储存的优先经验回放机制，更多采样对网络模型参数更新作用大的经验数据，具体过程如下：

1）计算训练数据优先级p。以TD-error为价值标准对训练数据的优先级进行衡量^[24-26]：

式中，TD-error为在时序差分（temporal-difference，TD）中当前估计的Q值和其目标Q值的损失差值。当损失差值越大时，证明该组训练数据需要进一步地学习和探索，优先级更高；为大于0的小常数，用于保证所有的p>0。

2）存储训练数据及其优先级至树形结构经验池。在马尔科夫博弈中，会持续产生新的训练数据并存入经验池，得到网络模型训练所需的经验数据，因此经验池始终保持更新状态。若每次更新都对池中经验数据按优先级排序将非常耗时，影响网络模型训练速度。为此，本文利用树形结构解决这一问题。在树形结构的叶子节点上存储每组训练数据及其优先级（D，p）作为经验数据，而父节点只需存储两个分叉子节点优先级之和p_和=p_j+p_k，根节点为所有经验数据优先级之和p_总=∑p_j，采用这种数据结构，可以省去训练数据按优先级排序的过程，大大降低计算复杂度。

3）计算经验数据的采样概率P^j_i。采样时，将根节点的优先级之和除以采样量m，分成m个区间，在每个区间内随机选取一个数，并选择该数对应的经验数据，从而采样到m组经验数据。智能体i采样第j组经验数据D_j概率P^j_i为

式中，k为当前经验池中储存的经验数据个数，p^j_i为智能体i抽取的第j组经验数据的优先级，α为一个0到1的数，用来控制随机采样和贪婪采样的调节系数。

4）使用重要性采样权重修正经验数据分布。未使用PER时，经验池中的经验数据服从独立同分布，而PER会有偏地改变这一分布，比如一个TD-error较大的经验数据A，网络模型在梯度下降时总会从A方向进行。因此还需加入重要性采样方法，这样既保证每组经验数据被选到的概率不同，加快训练速度，又保证在训练时每个经验数据在梯度下降时的影响相同，从而保证结果收敛。智能体i采样D_j经验数据重要性采样权重ω^j_i定义为

式中，m为样本数；β为一个0到1的采样偏置指数，用来调整偏置修正程度，在代码设置中β会随训练次数线性递增。同时为防止计算中浮点数的误差累计造成误差爆炸，对采样权重ω^j_i进行归一化处理：

式中，max_i，k（ω^k_i）为m组经验数据内最大经验数据权重，k为最大经验数据权重的序号。

1.2.2 3线程并行Critic网络模型的P3C-MADDPG网络架构

1）3线程并行Critic网络模型设计

MADDPG算法中，目标Critic网络以最大值作为期望值获得其Q值，相对于真实期望Q值普遍存在高估问题，将最终导致策略网络训练迭代目标不准确，影响生成策略的智能性，例如：无人机在避障、防碰上不够智能，对策略未知逃逸无人机的跟踪缺乏持续性。为此，在P3C-MADDPG算法中，通过构建3线程并行Critic网络模型，通过对3线程并行Critic网络的输出Q值求平均，从而降低Q值。若采用2线程并行Critic网络的输出Q值求平均，对Q值的高估校正幅度太小，采用3线程以上并行Critic网络的输出Q值求平均时，计算量过大，影响算法训练速度，因此选择设计3线程并行Critic网络。

3线程并行Critic网络模型的P3C-MADDPG网络架构如图2所示，每个智能体具备8个网络，分别为1个当前Actor网络和1个目标Actor网络，3个当前Critic网络和3个目标Critic网络。训练时，只训练当前网络并更新其参数，目标网络参数在当前网络参数更新一定次数后，依据其参数进行更新。因此设计目标Actor网络和3线程并行目标Critic网络目的：一是防止训练中，每次网络参数更新幅度过大导致训练过程不稳定；二是采用时序差分法，将目标网络输出的Q值作为真实Q值，再通过贝尔曼方程计算目标函数用于得到Critic网络的损失。

2）P3C-MADDPG网络训练

第一步：智能体i选取经验池中第j组经验数据D_j=（S^j_t，A^j_t，R^j_t，S^j_t+1）进行训练，其中全局状态S^j_t=（s^j_t，1，…，s^j_t，N），A^j_t=（a^j_t，1，…，a^j_t，N），R^j_t=（r^j_t，1，…，r^j_t，N），S^j_t+1=（s^j_t+1，1，…，s^j_t+1，N），N為智能体的个数，（s^j_t，i，a^j_t，i，r^j_t，i，s^j_t+1，i）为智能体i局部状态。Actor网络采用“去中心化”方式执行，输入智能体i分别在时刻t和t+1的局部观测状态s^j_t，i和s^j_t+1，i，输出决策动作a^j_t，i和a^j_t+1，i，3线程并行Critic网络采用“中心化”训练，分别依据全局观测状态S^j_t、S^j_t+1和全局动作状态A^j_t、A^j_t+1对智能体i的状态动作进行评价，得到Q_1，i、Q_2，i、Q_3，i和Q′_1，i、Q′_2，i、Q′_3，i值。因此，P3C-MADDPG算法属于“中心化训练、去中心化执行”类型的算法。

目标函数y^j_i为

式中，r^j_t，i为智能体i在t时刻动作奖励值；γ为折扣因子。

智能体i的3线程并行当前Critic网络的损失函数L_i，η（w^t_i，η）定义为

式中，t为当前时刻；m为抽取的样本数量；η为Critic网络编号，η=1，2，3；Q_η，i（S^j_t，A^j_t;w^t_i，η）为当前第η个Critic网络通过第j组经验数据输出的状态动作值；w^t_i，η为第η个当前Critic网络参数；y^j_i为目标函数值；ω^j_i为第j组经验数据的重要性采样权重，对PER带来的经验数据分布偏差进行修正。

第二步，利用随机梯度下降法更新当前Critic网络参数w^t+1_i，η，表示为

式中，w^t+1_i，η为智能体i在t+1时刻第η个当前Critic的网络参数；α为Critic网络的学习率；▽·表示梯度计算。

第三步，随机选择1个当前Critic网络输出的Q值计算Actor网络梯度▽_θ^t_iJ，利用梯度上升法，更新Actor网络参数θ^t+1_i，表示为：

式中，θ^t_i为智能体i在t时刻当前Actor网络的网络参数；θ^t+1_i为其t+1时刻当前Actor的网络参数；β为Actor网络的学习率参数；▽·表示梯度計算。

第四步，更新目标Actor和Critic网络参数θ^t+1′_i、w^t+1′_i，η，表示为：

式中，τ为0到1的常数。

2 基于P3C-MADDPG算法的多无人机协同追捕对抗策略

2.1 任务描述与建模

2.1.1 策略未知逃逸无人机环境中多无人机协同追捕对抗任务描述

如图3所示，策略未知逃逸无人机环境中，多无人机协同追捕对抗任务表示为在一个大小已知的二维平面空域内，由n架追捕无人机对一架策略未知逃逸无人机进行追捕、监视和驱离。追捕无人机的追捕策略和逃逸无人机的逃逸策略都通过P3C-MADDPG算法生成，双方在不断对抗训练中完善自身策略。图中，p_nn=1，2，3和e分别代表追捕无人机和逃逸无人机，v_i=v_ix，v_iyi=p_n，e为追逃双方无人机的速度，其中v_ix、v_iy分别为无人机沿x轴、沿y轴的速度分量，d_cap为追捕无人机对逃逸无人机的有效监视距离，d_saf为旋翼式无人机的最小安全飞行空间。

追捕成功的条件：在规定时间120 s内，所有追捕无人机与逃逸无人机的距离d_pne满足d_cap≥d_pne≥d_saf，且v_pn和v_e方向一致，|v_pn|-|v_e|≤0.3 m/s。

逃逸成功的条件：在规定时间120 s内逃逸无人机与所有追捕无人机的最小距离min d_pne>d_cap。

追捕过程中约束条件：1）任意两架无人机之间的距离d_ij>d_saf；2）无人机不能碰到无规则边界障碍物；3）无人机不能超出边界。

2.1.2 旋翼式无人机运动学模型建立

以旋翼式无人机^[27]为例，建立无人机运动学方程为

式中，x_i，y_i为无人机的位置；a_i为无人机的加速度，a_ix、a_iy分别为无人机沿x轴、沿y轴的加速度。

在无人机实际控制中，受动力因素的影响，其速度、加速度的约束限制为

式中，a_xmax、a_ymax分别为无人机在x轴、y轴的最大加速度；v_max为无人机最大速度。

无人机的运动范围不能超出环境边界，其位置需满足：

式中，x_min、x_max、y_min、y_max分别为环境边界的最小、最大横坐标和最小、最大纵坐标。

2.2 多无人机协同追捕对抗策略的训练要素设计

依据1.1节可知，P3C-MADDPG算法决策时需要获取环境状态信息S，从无人机所有可能执行的动作中确定一个动作A输出并执行，同时对动作好坏给予相应奖励R。因此，需要结合在策略未知逃逸无人机环境中多无人机协同追捕对抗任务，为基于P3C-MADDPG算法生成多无人机协同追捕对抗策略设计所需的训练元素，包括追逃无人机的状态空间、稀疏奖励与引导式奖励相结合的奖励函数、加速度不同的追逃动作空间。

2.2.1 状态空间设计

狀态空间S是无人机与环境交互时，能够获取环境中有价值的全部信息，也是无人机做出良好决策的重要依据。全面合理的状态空间可以确保多无人机在强化学习算法控制下完成追捕对抗任务。因为P3C-MADDPG算法的特点是“中心化训练，去中心化执行”，所以在训练结束执行时，是一个完全分布式的控制方法，无人机只需掌握自身局部观测信息，无须与其他无人机之间进行通信。

追捕无人机的状态空间S_p主要包括自身信息s_pi、友方信息s_pj、逃逸无人机信息s_e、约束条件信息inf，表示为

自身信息s_pi包含自身位置坐标和加速度；友方信息s_pj包含两架友方无人机的相对位置坐标；逃逸无人机信息s_e包含逃逸无人机的相对位置和加速度；约束条件信息inf包含与其他无人机是否碰撞、是否躲避障碍物、是否超出边界。

逃逸无人机的状态空间S_e主要包括自身信息s_e、追捕无人机信息s_pn、约束条件信息inf，表示为：

自身信息s_e包含自身位置坐标和加速度；追捕无人机信息s_pn包含n架追捕无人机的相对位置；约束条件信息inf包含与其他无人机是否碰撞、是否躲避障碍物、是否超出边界。

2.2.2 奖励函数设计

奖励函数R依据追捕和逃逸任务以及约束条件，将稀疏奖励和引导式奖励相结合，解决稀疏奖励造成的算法难收敛问题。引导式奖励对无人机追逃过程中每个动作都给予奖励或惩罚，稀疏奖励只在目标达成时给予奖励，两者结合既能引导无人机不断接近目标，也能在无人机达到目标时给予与其他动作不同的奖励。追捕和逃逸无人机的目标任务相反，分别设计其奖励函数。

追捕无人机奖励函数R_p（其中01，a₂，a₃，a₄，a₅<1为调节系数，且满足a₁+a₂+a₃+a₄+a₅=1）设计为：

1）追捕距离奖励R_p1

为保证追捕任务的时效性，每时间步长会收到负奖励，通过引导式奖励使得追捕无人机快速追捕。

2）追捕成功奖励R_p2

当满足追捕成功条件时，采用稀疏奖励给予追捕无人机正向反馈。

3）碰撞奖励R_p3

当两架无人机之间距离小于最小安全飞行空间距离，说明两架飞机发生了碰撞危险，对这一错误行为采用稀疏奖励给予惩罚。

4）避障奖励R_p4

式中，d_iz为无人机与障碍物的距离。当无人机与无规则形状的山体障碍物和云朵障碍物发生碰撞时，采用稀疏奖励对当前位置状态下的无人机行为动作给予惩罚。

5）边界奖励R_p5

式中，d_ib为无人机与边界的距离。当无人机距离边界距离小于无人机最小安全飞行空间距离时，表征无人机飞行位置超出空域边界，采用稀疏奖励给予惩罚。

逃逸无人机奖励函数R_e设计为：

1）逃逸距离奖励R_e1

式中，b₁为调节系数（01<1）。当逃逸无人机超出追捕无人机的有效监视距离时，采用引导式的奖励引导逃逸无人机远离追捕无人机。

2）逃逸无人机在碰撞奖励R_e2、避障奖励R_e3、边界奖励R_e4与追捕无人机设计完全相同。

2.2.3 动作空间设计

动作空间A包括无人机在追捕对抗任务中可能执行的所有行为，一般坚持简单高效的原则，本文以旋翼式无人机为例设计动作空间。

旋翼式无人机在角速度上要求较低，主要通过横向和纵向的加速度对无人机进行控制，因此动作空间设计为沿x轴加速度a_ix、沿y轴加速度a_iy。假设逃逸无人机选用动力更强的旋翼式无人机，两者动作空间参数相同，但逃逸无人机的数值更大。动作空间A表示为

2.3 基于P3C-MADDPG算法的多无人机协同追捕对抗策略生成

基于P3C-MADDPG算法的多无人机协同追捕对抗策略生成过程如表1所示。

3 仿真实验与分析

本节通过建立策略未知逃逸无人机环境中多无人机协同追捕对抗环境，对P3C-MADDPG算法在训练快速性、降低Q值高估有效性、生成的多无人机协同追捕对抗策略的智能性进行验证。

3.1 实验环境及参数设置

实验采用Pycharm Community 2023.1和Anaconda3平台，仿真环境使用Python语言编写，深度学习框架采用Pytorch1.10模块，强化学习环境框架采用OpenAI Gym0.10.5模块。训练超参数设置如表2所示。

多无人机协同追捕对抗任务实验环境示意图如图4所示，环境参数设置如表3所示。对抗环境在一个长100 m、宽60 m的二维战场区域内，战场内存在两个无规则边界的山体障碍物和云朵障碍物，障碍物位置固定。3架追捕无人机和1架逃逸无人机从初始位置出发，分别在P3C-MADDPG算法的控制下进行追逃对抗任务，实验规定在120 s的时间内，任意一方在满足约束条件的情况下达到追捕成功或逃逸成功者获胜。

3.2 算法训练快速性實验

为验证P3C-MADDPG算法相对于应用优先经验回放机制的PER-MADDPG算法在训练快速性上更加优越，本次实验进行150局的训练，将每局中追捕无人机的平均累计收益奖励收集并绘制收益曲线图，曲线增长越快说明算法训练时间越短。PER-MADDPG算法累计收益奖励曲线图如图5所示，P3C-MADDPG算法累计收益奖励曲线图如图6所示。

图中横坐标为训练局数，纵坐标为3架追捕无人机在每局训练中平均累计收益奖励值。从图5和图6中可以看出，刚开始训练时，追捕无人机处于探索阶段，累计收益奖励较低，随着训练次数增多，追捕无人机的追捕策略逐渐智能化，累计收益奖励增高。对于PER-MADDPG算法，在训练第60局时累计收益奖励曲线基本实现平稳，算法基本收敛。P3C-MADDPG算法在训练第50局时累计收益奖励开始实现平稳，算法实现收敛状态。可见P3C-MADDPG算法的收敛速度明显更快，并在收敛区域内的累计收益奖励曲线更加平稳。

通过多次实验，每次实验达到收敛时，P3C-MADDPG算法所需训练局数以及相对于PER-MADDPG算法在训练快速性上的提升率如表4所示。在训练快速性上P3C-MADDPG算法相对于PER-MADDPG算法平均提升11.7%。

3.3 降低Q值高估实验

为验证P3C-MADDPG算法在降低Q值高估的有效性。在训练过程中，统计两种算法的目标Q值如图7所示，横坐标为训练次数，纵坐标为训练中目标Critic网络估计Q值的累计值，本次实验中P3C-MADDPG算法在训练过程中降低目标Q值高估6.25%。通过多次实验，目标Q值高估降低率如表5所示。可见P3C-MADDPG算法有效平均降低目标Q值高估6.06%，改进效果明显。

3.4 策略智能性实验

为验证基于P3C-MADDPG算法生成的策略相对于MADDPG算法更具智能性，将两种算法都应用于生成多无人机协同追捕对抗策略，通过实验结果分析两种策略的控制效果哪种更佳。经过150局的训练，两种策略的控制效果如图8所示。

图8a）中，对于第一种策略，d_p1p₃=6.03 m>d_saf=6 m快要碰撞时，两者的速度V_p1和V_p3并没有改变航向，继续保持原有方向继续飞行，可以看出两架追捕无人机没有学会在这种状态下如何防止碰撞，而且P₃和E无人机都出现了与边界距离为d_p3b=1.02 msaf/2，d_eb=0.89 msaf/2的情况，远离边界的策略不佳；对于第二种策略，在d_p1z=5.46 m，d_ez=3.12 m时（接近无人机最小安全飞行空间距离的一半d_saf/2=3 m），P₁无人机和E无人机都改变了原有的运动趋势，做出了远离山体的动作，学会了如何规避障碍物，使得自身具备躲避障碍物的能力。

图8b）中，对于第一种策略，在d_p2b=7.82 m时，P₂无人机能够转变运动方向远离战场边界。在d_p3z=5.31 m时，P₃无人机能够减速并转变运动方向，具备了避障能力；对于第二种策略，d_p1p₃=7.27 m时，V_p1p3且方向不同，P₁和P₃无人机都自主地采取动作防止碰撞，具备了己方之间防碰撞的能力。同时d_p3b=4.74 m时，P₃无人机改变运动方向远离战场边界，具备远离边界的能力。

图8c）中，红色虚线圆半径为7 m。两种策略实现了三架追捕无人机与逃逸无人机的距离d_pne满足d_cap≥d_pne≈7 m≥d_saf，速度V_pn和V_E方向一致，|V_pn|-|V_E|≤0.1 m/s≤0.3 m/s。但第一种策略在监视过程中，当d_p2z=2.6 msaf/2时，P₂无人机没有改变运动方向，会与山体障碍物发生碰撞，不满足约束条件。从图8d）可知，第一种策略在140 s时追捕无人机追到逃逸无人机，第二种策略只用了120 s，因此，只有第二种基于P3C-MADDPG算法生成的策略满足所有追捕成功条件。

从整体追捕效果分析，基于P3C-MADDPG算法的策略实现了三架追捕无人机对逃逸无人机的追捕，基于MADDPG算法的策略在追捕过程中出现多种不满足约束条件的情况，而且达到稳定监视状态的用时较长。因此，基于P3C-MADDPG算法的策略能够使得无人机学会自主处理无人机之间防碰撞、与障碍物避障、远离边界等问题，并且三架追捕无人机相互之间协同对快速移动的逃逸无人机完成了追捕。

4 结束语

本文针对策略未知逃逸无人机环境中多无人机协同追捕对抗任务，提出P3C-MADDPG算法的多无人机协同追捕对抗策略。通过实验证明，P3C-MADDPG算法在训练速度上平均提升11.7%，Q值平均降低6.06%，多无人机协同追捕对抗策略不仅满足避障、防碰、不超出边界的约束条件，而且能够更好地完成对策略未知逃逸无人机的智能追捕。

1）提出P3C-MADDPG算法。在理论上阐述P3C-MADDPG算法如何加快训练速度和解决Q值高估问题，介绍P3C-MADDPG算法的设计原理，着重对算法中，基于树形结构的优先经验回放机制和3线程并行Critic网络模型的P3C-MADDPG算法网络架构进行详细阐述。

2）基于P3C-MADDPG算法生成多无人机协同追捕对抗策略。通过构建旋翼式无人机运动学模型，设计追逃无人机的状态空间、稀疏奖励与引导式奖励相结合的奖励函数、加速度不同的追逃动作空间等训练要素，采用P3C-MADDPG算法生成策略未知逃逸无人机环境中多无人机协同追捕对抗策略。

参考文献：

[1] 朱超磊， 金钰， 王靖娴， 等. 2022年国外军用无人机装备技术发展综述[J]. 战术导弹技术， 2023（3）： 11-25， 31.

ZHU C L， JIN Y， WANG J X， et al. Overview of the development of foreign military UAV systems and technology in 2022[J]. Tactical Missile Technology， 2023（3）： 11-25， 31.

[2] 樊會涛， 闫俊. 空战体系的演变及发展趋势[J]. 航空学报， 2022， 43（10）： 527397.

FAN H T， YAN J. Evolution and development trend of air combat system[J]. Acta Aeronautica et Astronautica Sinica， 2022， 43（10）： 527397.

[3] SHAO S K， LI H Z， ZHAO Y J， et al. A new method for multi-UAV cooperative mission planning under fault[J]. IEEE Access， 2023（11）： 52653-52667.

[4] ZHANG J D， YANG Q M， SHI G Q， et al. UAV cooperative air combat maneuver decision based on multi-agent reinforcement learning[J]. Journal of Systems Engineering and Electronics， 2021， 32（6）： 1421-1438.

[5] XU C， XU M， YIN C J. Optimized multi-UAV cooperative path planning under the complex confrontation environment[J]. Computer Communications， 2020（162）： 196-203.

[6] 王文飞， 茹乐， 陈士涛， 等. 基于元模型的有人/无人机协同空战概念研究[J]. 电光与控制， 2022， 29（12）： 51-57.

WANG W F， RU L， CHEN S T， et al. Research on the concept of manned/unmanned aerial combat based on metamodel[J]. Electronics Optics & Control， 2022， 29（12）： 51-57.

[7] 张云赫， 苏立晨， 董云帆， 等. 基于Voronoi图最近邻协商的多机协同追捕方法[J]. 哈尔滨工程大学学报， 2023， 44（2）： 284-291.

ZHANG Y H， SU L C， DONG Y F， et al. Cooperative pursuit of multiple UAVs based on Voronoi partition nearest neighbor negotiation[J]. Journal of Harbin Engineering University， 2023， 44（2）： 284-291.

[8] 张澄安， 邓文， 王李瑞， 等. 基于阿波罗尼奥斯圆的无人机追逃问题研究[J]. 航天电子对抗， 2021， 37（5）： 40-43， 48.

ZHANG C A， DENG W， WANG L R， et al. Research on UAV pursuit and evasion based on Apollonius circle[J]. Aerospace Electronic Warfare， 2021， 37（5）： 40-43， 48.

[9] 于月平， 袁莞迈， 段海滨. 仿鹰-欧椋鸟智能行为的无人机集群追逃控制[J]. 指挥与控制学报， 2022， 8（4）： 422-433.

YU Y P， YUAN W M， DUAN H B. Pursuit-evasion control for UAV swarm imitating the intelligent behavior in hawks-starlings[J]. Journal of Command and Control， 2022， 8（4）： 422-433.

[10]彭雅兰， 段海滨， 张岱峰， 等. 仿灰狼合作捕食行为的无人机集群动态任务分配[J]. 控制理论与应用， 2021， 38（11）： 1855-1862.

PENG Y L， DUAN H B， ZHANG D F， et al. Unmanned aerial vehicle swarm dynamic mission planning inspired by cooperative predation of wolf-pack[J]. Control Theory & Applications， 2021， 38（11）： 1855-1862.

[11]HAN X Y. Application of reinforcement learning in multiagent intelligent decision-making[J]. Computational Intelligence and Neuroscience， 2022： 1-6.

[12]章胜， 周攀， 何扬， 等. 基于深度强化学习的空战机动决策试验[J]. 航空学报， 2023， 44（10）： 122-135.

ZHANG S， ZHOU P， HE Y， et al. Air combat maneuver decision-making test based on deep reinforcement learning[J]. Acta Aeronautica et Astronautica Sinica， 2023， 44（10）： 122-135.

[13]许旭升， 党朝辉， 宋斌， 等. 基于多智能体强化学习的轨道追逃博弈方法[J]. 上海航天（中英文）， 2022， 39（2）： 24-31.

XU X S， DANG Z H， SONG B， et al. Method for cluster satellite orbit pursuit-evasion game based on multi-agent deep deterministic policy gradient algorithm[J]. Aerospace Shanghai（Chinese & English）， 2022， 39（2）： 24-31.

[14]王钦钊， 多南讯， 吕强， 等. 基于强化学习的多智能体合作博弈对抗算法[J]. 装甲兵学报， 2022， 1（5）： 80-85.

WANG Q Z， DUO N X， LYU Q， et al. Multi-agent cooperative game confrontation algorithm based on reinforcement learning[J]. Journal of Armored Forces， 2022， 1（5）： 80-85.

[15]符小卫， 徐哲， 王辉. 基于DDPG的无人机追捕任务泛化策略设计[J]. 西北工业大学学报， 2022， 40（1）： 47-55.

FU X W， XU Z， WANG H. Generalization strategy design of UAVs pursuit evasion game based on DDPG[J]. Journal of Northwestern Polytechnical University， 2022， 40（1）： 47-55.

[16]高昂， 董志明， 李亮， 等. MADDPG算法并行优先经验回放机制[J]. 系统工程与电子技术， 2021， 43（2）： 420-433.

GAO A， DONG Z M， LI L， et al. Parallel priority experience replay mechanism of MADDPG algorithm[J]. Systems Engineering and Electronics， 2021， 43（2）： 420-433.

[17]乔哲， 黎思利， 王景志， 等. 基于PER-PDDPG的无人机路径规划研究[J]. 无人系统技术， 2022， 5（6）： 12-23.

QIAO Z， LI S L， WANG J Z， et al. UAV path planning based on PER-PDDPG[J]. Unmanned Systems Technology， 2022， 5（6）： 12-23.

[18]魏瑶， 刘志成， 蔡彬， 等. 基于深度循环双Q网络的无人机避障算法研究[J]. 西北工业大学学报， 2022， 40（5）： 970-979.

WEI Y， LIU Z C， CAI B， et al. Research on UAV obstacle avoidance algorithm based on deep cycle double Q network[J]. Journal of Northwestern Polytechnical University， 2022， 40（5）： 970-979.

[19]丁世飞， 杜威， 郭丽丽， 等. 基于双评论家的多智能體深度确定性策略梯度方法[J]. 计算机研究与发展， 2023， 60（10）：2394-2404.

DING S F， DU W， GUO L L， et al. Multi-agent deep deterministic policy gradient method via double critics[J].Journal of Computer Research and Development， 2023， 60（10）：2394-2404.

[20]YUAN W， LI Y Y， ZHUANG H Y， et al. Prioritized experience replay-based deep Q learning： multiple-reward architecture for highway driving decision making[J]. IEEE Robotics & Automation Magazine， 2021， 28（4）： 21-31.

[21]张严心， 孔涵， 殷辰堃， 等. 一类基于概率优先经验回放机制的分布式多智能体软行动-评论者算法[J]. 北京工业大学学报， 2023， 49（4）： 459-466.

ZHANG Y X， KONG H， YIN C K， et al. Distributed multi-agent soft actor-critic algorithm with probabilistic prioritized experience replay[J]. Journal of Beijing University of Technology， 2023， 49（4）： 459-466.

[22]XU D， CHEN G. Autonomous and cooperative control of UAV cluster with multi-agent reinforcement learning[J]. The Aeronautical Journal， 2022， 126（1300）： 932-951.

[23]刘诗诚. 基于深度强化学习的多智能体覆盖控制研究[D]. 秦皇岛： 燕山大学， 2022.

LIU S C. Research on multi-agent coverage control based on deep reinforcement learning[D]. Qinhuangdao： Yanshan University， 2022.

[24]胡皓然. 多智能体强化学习算法研究与应用[D]. 北京： 北京邮电大学， 2021.

HU H R. Research and implementation on multi-agent reinforcement learning[D]. Beijing： Beijing University of Posts and Telecommunications， 2021.

[25]赵英男， 刘鹏， 赵巍， 等. 深度Q学习的二次主动采样方法[J]. 自动化学报， 2019， 45（10）： 1870-1882.

ZHAO Y N， LIU P， ZHAO W， et al. Twice sampling method in deep Q-network[J]. Acta Automatica Sinica， 2019， 45（10）： 1870-1882.

[26]刘颖. 深度强化学习中的经验回放研究[D]. 南京： 东南大学， 2021.

LIU Y. Research on experience replay in deep reinforcement learning[D]. Nanjing： Southeast University， 2021.

[27]劉云辉， 石永康. 未知环境下多无人机协同搜索与围捕策略研究[J]. 现代电子技术， 2023， 46（6）： 98-104.

LIU Y H， SHI Y K. Research on cooperative search and round up strategy of multiple-UAV in unknown environment[J]. Modern Electronics Technique， 2023， 46（6）： 98-104.

（责任编辑：许韦韦）