基于PLS-BP神经网络的数控机床热误差建模研究
2023-12-12王文辉苗恩铭唐光元冯天勤
王文辉,苗恩铭,唐光元,冯天勤
(重庆理工大学 机械工程学院, 重庆 400054)
0 引言
数控机床热误差对零件的加工精度影响显著,研究表明热误差占机床总误差的40%~70%[1-3]。以热误差模型为核心的软件补偿方法因成本低、灵活度高的优势,成为现代机床热误差研究中的主流趋势[4]。
数控机床热误差软件补偿的核心问题是建立预测精度高、稳健性强的数学模型[5]。目前,反向传播(back propagation,BP)神经网络具有较强的非线性映射能力、高度自学习和自适应的能力[6-7],在描述复杂非线性的温度-热误差关系时具有优势,受到许多学者的关注。Yang等[8]建立神经网络模型,提高机床在不同切削条件下的预测精度;谭峰等[9]建立BP神经网络热误差模型,提高机床主轴的预测精度;伍伟敏等[10]基于BP神经网络搭建五轴数控机床热误差补偿模型,能够有效提高机床的加工精度。辛宗霈等[11]建立神经网络模型,提高了丝杆热变形量的预测精度。
上述研究中,BP神经网络在一定程度上可以提高模型的预测精度,但该算法在训练过程中容易受到冗余信息的干扰,使得模型难于快速确定最佳的权值和阈值,陷入局部最优,导致模型预测精度下降。因此,在机床热误差补偿建模中,BP模型的预测精度会出现提高和降低的现象,其稳健性较差,无法同时满足模型预测精度和稳健性的要求。
经研究发现,偏最小二乘(partial least squares,PLS)算法对自变量进行降维处理,提取主成分,能消除其所包含的冗余信息,有效提高模型的稳健性[12-13]。本文在BP神经网络建模的基础上,提出增加PLS算法的数据前处理方法,消除冗余信息的干扰,从而快速准确地获得模型的最佳权值和阈值,提高模型稳健性,称此方法为PLS-BP神经网络。
本文中,以台中精机Vcenter-55型数控加工中心为研究对象,采用传统BP神经网络算法建模,分析预测精度和稳健性性能。同时,采用所提PLS-BP神经网络方法进行建模预测,并与传统BP模型的预测效果进行对比分析,以验证PLS-BP模型的有效性和优越性。
1 热误差建模算法
1.1 BP神经网络
BP神经网络是一种多层前馈性神经网络,模型为节点构成的拓扑结构,包含输入层、隐含层和输出层[14],结构如图1所示。

图1 BP神经网络模型结构示意图
采用“2-5-1”BP神经网络热误差模型,输入层2个节点表示为2个温度敏感点输入变量;中间隐含层有5个节点;输出层1个节点为热误差数据。
在BP神经网络中,正向传播时输入信号经权值和阈值处理传递给隐含层,经隐含层神经元的传递函数处理后输出,逐层传递,最终输出信号。输出信号与热误差之间的残差作为误差信号,当误差信号过大时,则进行反向传播,将误差信号沿原来的通道返回,修改各层节点的权值和阈值使误差信号最小,重复训练最终得出网络模型。
1.2 PLS-BP神经网络
BP神经网络的高度自学习和自适应能力使模型的预测精度有所提升,但训练过程中容易受冗余信息的干扰,使得模型无法快速确定最佳权值和阈值,导致模型预测精度的稳健性下降。而在工程实践中,模型需同时满足精度和稳健性要求,故传统BP模型存在一定的缺陷。PLS算法对温度数据进行降维处理,并保留温度数据与热误差之间的相关性,用无相关性的主成分变量参与回归建模,可提高模型的稳健性[15]。
结合上述2种算法的优点,构建PLS-BP神经网络。使用PLS算法计算出主成分变量,用主成分变量作为输入信号建立BP模型。算法建模步骤如下:
设温度数据X(N×m)=[x1x2…xm],热误差数据Y(N×n)=[y1y2…yn],样本点个数为N。
步骤1将温度数据和热误差数据标准化,得到X0和Y0,然后分别提取X0和Y0的第一主成分t1和u1,保证t1和u1保留各原始数据的主要特征,且t1和u1之间的相关性达到最大,计算公式如下:
(1)
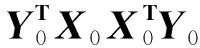
步骤2建立X0和Y0关于主成分t1的回归模型:
(2)
式中:p1=[p11,p12,…,p1m],q1=[q11,q12,…,q1n]分别为回归模型中的参数向量;X1和Y1分别为残差矩阵。
步骤3用残差矩阵X1和Y1替换X0和Y1重复上述步骤以进一步提取主成分,直至所提主成分贡献率超过95%。
步骤4假设最终通过PLS算法提取到r个主成分t1、t2、…、tr,将其作为神经网络的输入层,热误差数据Y作为输出层,搭建PLS-BP神经网络模型。
2 热误差测量实验
以Vcenter-55型数控加工中心作为被测对象,同步采集数控机床的热误差和温度,如图2所示。

图2 Vcenter-55数控立式加工中心实物图
热误差测量采用“五点测量法”,在X向和Y向上各布置2个电涡流传感器,Z向布置1个,如图3所示。电涡流传感器型号为ZH3010,量程为1 mm,测量精度为1 μm。
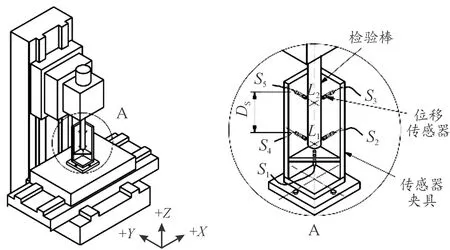
图3 五点测量法示意图
温度测量方面,使用20个型号为DS18B20的温度传感器在机床的主要热源附近进行测量,测量范围为-55~125 ℃,编号记作T1~T20,安放位置如表1所示。
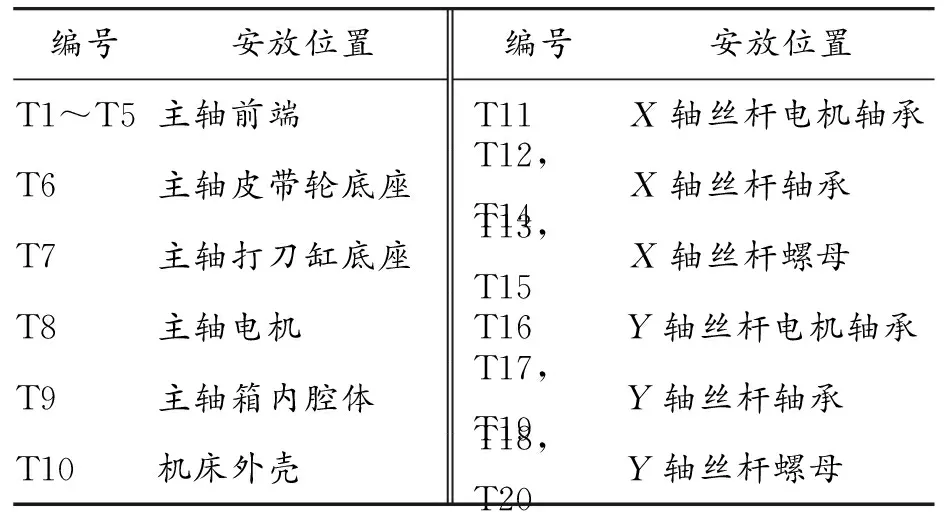
表1 温度传感器安放位置
依据上述实验装置,主轴以恒定转速2 500 r/min空转,每次实验持续时间达到7 h以上,累计获得机床在横跨3—9月份不同季节下的K1—K6批次实验数据,如表2所示。由于温度数据结果较多,本文中仅展示K1批次的部分温度数据,如图4所示。
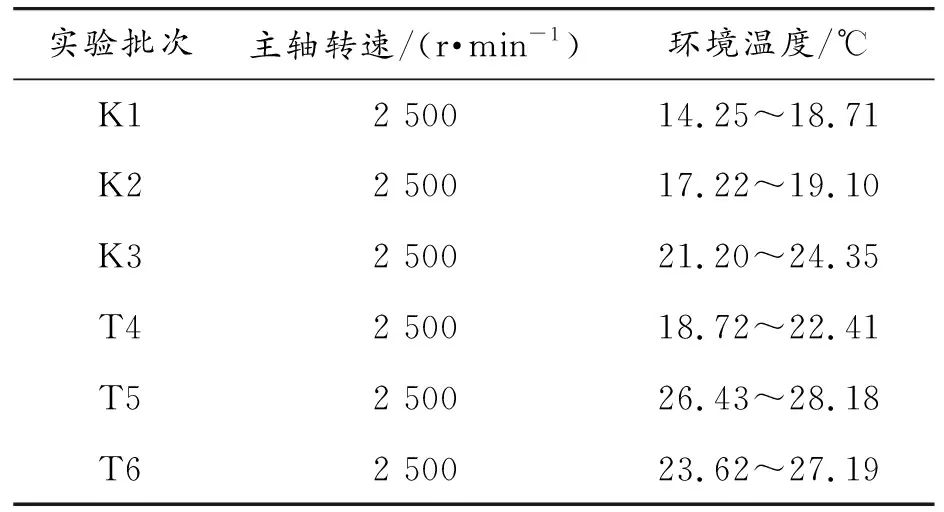
表2 实验数据

图4 K1批次部分温度曲线
因机床X轴和Y轴的热误差较小,故以Z向热误差数据进行建模和预测,得出K1—K6批次的热误差数据如图5所示。不难看出,在跨季过程中,热变形规律差异较大,因此所建补偿模型必须考虑稳健性。

图5 K1—K6批次的Z向热误差曲线
3 温度敏感点的选择
热误差数据建模前需要从诸多温度监测点中选择合适的温度敏感点,以避免过多的输入变量可能存在的共线性问题[16-17]。使用模糊聚类结合灰色关联度的方法[18-19]选择温度敏感点,6批次数据计算结果如表3所示。
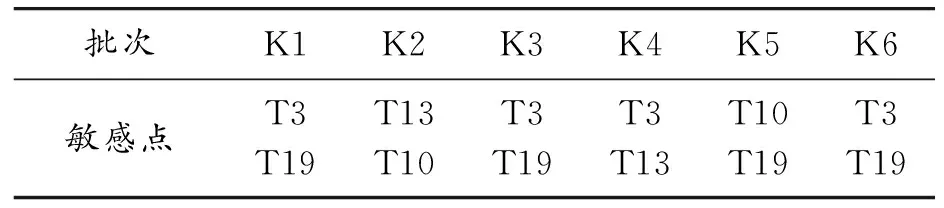
表3 温度敏感点数据计算结果
4 热误差建模及模型稳健性精度分析
针对数控加工中心Z向热误差建模对比分析,先用传统BP神经网络算法建模,分析其预测精度和稳健性。采用本文的PLS-BP神经网络进行建模预测,并与传统BP预测效果进行对比分析,以验证PLS-BP模型的有效性和优越性。
4.1 BP建模
以K1批次数据建模为例,将温度敏感点T3和T19作为模型的输入信号,隐含层节点数设为5,Z向热误差作为输出层,训练得到网络模型。同理,得出K2—K6批次的BP模型。
为验证模型的预测效果,使用模型对其他批次数据进行预测。为判断模型的优劣性,以残余标准差S作为精度评判标准,见式(3)。而模型对其他批次数据预测的残余标准差的平均值Mn能够反映模型预测效果,用来表征模型的预测精度,计算见式(4);残余标准差的标准差Sd反映模型预测效果的波动性,用来表征模型的稳健性,计算见式(5)。
(3)
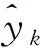
(4)

(5)
式中:Si为数据预测的残余标准差;K为预测数据的批次。
根据所建立的K1—K6批次的BP模型,对其他批次数据进行预测,得到各批次的预测残余标准差S,并计算S的均值Mn和S的标准差Sd用于模型稳健性精度分析,计算结果如表4所示。

表4 BP模型的残余标准差计算结果 μm
由表4可知,BP模型的Mn值分布范围为4.93~6.46 μm,Sd值分布范围为1.33~2.24 μm。
因BP算法在训练过程中易陷入局部最优,导致模型的预测精度下降。故将PLS算法与BP神经网络算法结合,用PLS算法对温度数据进行降维,去除冗余信息,实现对模型预测精度和稳健性的提升。
4.2 PLS-BP建模
以K1批次数据建模为例,对实验数据进行标准化处理,进而计算出主成分对。
(6)
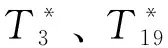
第1个主成分贡献率为85.56%<95%,因此选择2个主成分对,记作t=(t1,t2)。然后,用主成分t作为输入信号,以Z向热误差作为输出层,搭建PLS-BP神经网络模型,如图6所示。

图6 PLS-BP神经网络模型结构
作为参照对比,使用PLS-BP模型与K1批次所建立的BP模型分别预测K2批次数据,预测结果和残差值如图7和图8所示。残差值越小,模型的预测效果越好,计算见式(7)。
(7)
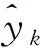

图8 K2预测残差
对比图7和图8的预测结果发现,BP模型残差分布在-3.42~9.42 μm;PLS-BP模型残差分布在-6.23~3.15 μm,波动范围更小。进一步地,计算2种模型的残余标准差S,如表5所示。相比之下,PLS-BP模型的S数值更小,为2.24 μm。由此可见,PLS-BP模型预测精度要优于BP模型。

表5 BP模型与PLS-BP模型预测精度
4.3 PLS-BP模型稳健性分析
为进一步体现PLS-BP模型的稳健性,用K1—K6批次实验数据之间相互预测,并计算残余标准差的平均值Mn和残余标准差的标准差Sd用于模型的稳健性分析,计算结果如表6所示。
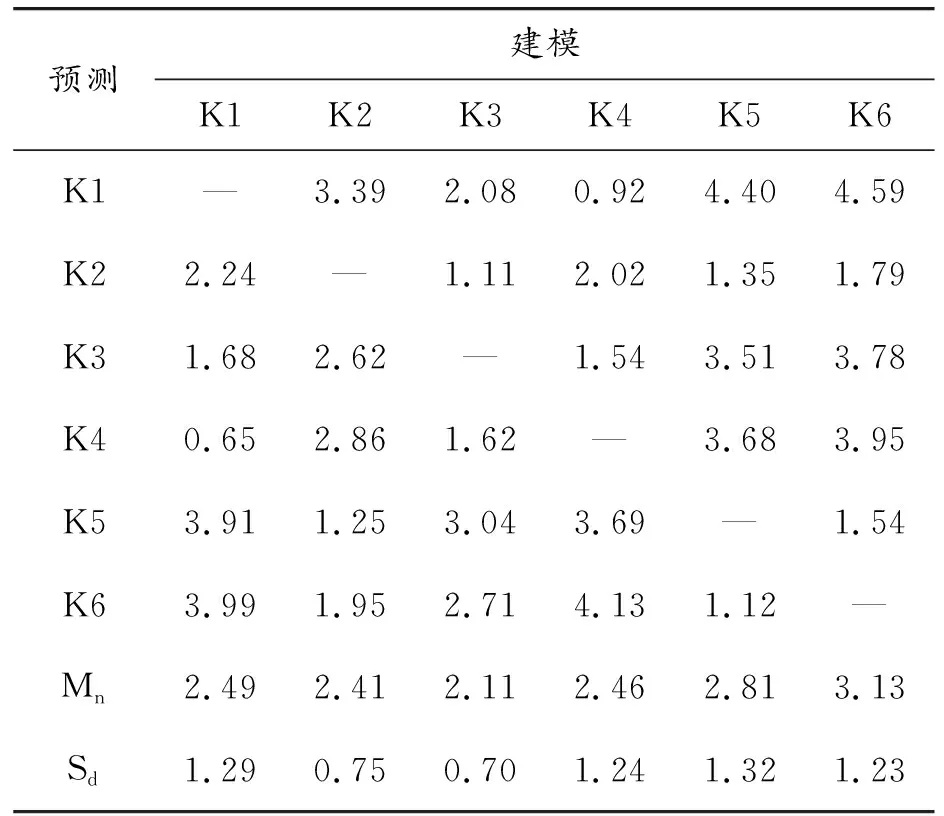
表6 PLS-BP模型的残余标准差计算结果 μm
综合评价PLS-BP模型的稳健性,将表6和表4中BP模型的预测效果进行对比,得出PLS-BP模型的最大Mn和Sd值分别为3.13 μm和1.32 μm,BP模型的最大Mn和Sd值分别为6.46 μm和2.24 μm,PLS-BP模型在数值上具有优势。
进一步绘制K1—K6单批次各模型的Mn和Sd直方图,直观对比模型的预测精度和稳健性,如图9和图10所示。

图9 BP和PLS-BP模型预测效果均值直方图

图10 BP和PLS-BP模型预测效果标准差直方图
通过图9、图10分析得出,PLS-BP模型的Mn和Sd值均低于BP模型,具有更好的预测精度和稳健性,且最大的Mn、Sd值分别出现在K6、K5批次所建的模型中,数值分别为3.13 、1.32 μm,低于BP模型最小的Mn值(4.93μm)和Sd值(1.33 μm)。
结果表明,PLS-BP模型相比于BP模型,稳健性得到较大提升,具有明显优势,能够更好地表达热误差与温度之间的关系。
5 结论
针对BP神经网络热误差模型存在的稳健性差的缺陷,提出基于PLS-BP神经网络的热误差建模方法。通过增加偏最小二乘降维处理,消除冗余信息,从而快速确定最佳权值和阈值,克服陷入局部最优的缺陷,提高模型的预测精度和稳健性,
建立Vcenter-55数控加工中心的热误差模型,多批次预测实验结果表明,所提PLS-BP模型可将预测残余标准差的最大均值和最大标准差分别控制在3.13 和1.32 μm以内,稳健性显著优于BP模型,对进一步提高热误差模型的精度和稳健性具有理论指导意义。
