动力锂离子电池风冷散热CFD仿真

王 盛,任润国,尉庆国,袁文奇

(1.中北大学 能源与动力工程学院, 太原 030051;2.山西新能源汽车工业有限公司, 山西 晋中 030600;3.内蒙古第一机械集团有限公司, 内蒙古 包头 014032)

0 引言

随着新能源汽车在全球范围内的大力推广,基于新能源赛车的汽车竞技运动得到了快速发展。赛车属于极限运动,其行驶工况相对普通民用汽车更加的极端和多变,动力电池系统极易出现过热或散热不良的现象[1-2]。在国外FE方程式世锦赛和国内FSEC方程式汽车大赛中,由于电池温升异常导致赛车失去动力的事件频频发生[3]。

近年来国内外技术人员对风冷散热系统做了大量研究。Saw等[4]和Qin等[5-6]用CFD方法对电池风冷散热系统的散热能力进行了仿真研究,通过实验验证了CFD仿真方法的可行性;Yang等[7-8]和张继华等[9]通过数值仿真的方法发现了电池箱内部空气流道、进出口位置、流体参数等因素会对电池包温升和温差变化有较大的影响;夏博妍[10]采用穷举法和遗传算法探究了进风速度、电池间隙等因素对散热系统的影响,并根据影响次序对于原方案进行了优化,优化后的方案有较好的散热效果,但整个探究过程工作量巨大,仿真实验达40余次;同样是风冷散热优化问题,李淼林等[11]采用正交试验法,通过较少次数的迭代计算,遴选出了较为理想的散热方案。综上,CFD数值仿真和正交实验法在风冷散热优化研究方面应用较为广泛,且可使研究工作效率更高。

为了解决电动赛车在FSEC竞赛中散热不良的问题[12],本文基于赛事工况,采用CFD数值仿真和正交试验相结合的方法,以最高温度和温差最小化作为优化目标,对原散热方案进行优化。同时为了减少非必要的迭代步骤,提高优化效率,本研究在考虑三大优化指标的同时将充分结合电池包温度的均布性和电池箱体热量的聚集情况等因素,对散热方案进行对比遴选和优化分析。最后将通过仿真计算和实车跑动试验相结合的方法,对新散热方案的可行性和仿真结果的可靠性进行验证。

1 电池Pack散热系统初步设计

1.1 电池Pack结构与组成

本文研究的是适配于FSEC电动方程式赛车的动力电池Pack,电池包共由35个单体电池分5个模组,按照35S1P的方式组合而成。所采用的单体电池是由中航锂电公司生产的L148N50B型方壳镍钴锰酸锂电池,长为148 mm,宽为26.8 mm,高为98 mm,额定容量为50 A,标称电压为3.65 V,最大电压为4.3 V,如图1所示。每个模组由7个单体电池串联组成,额定电压为25.55 V。整个电池Pack额定电压为127.75 V,额定能量为6.39 kW·h,最大电压为150 V,最大能量为7.525 kW·h。

图1 电池Pack散热系统的结构及简化模型

1.2 放电工况分析及热管理目标设定

为了近似模拟竞赛实际放电工况,同时考虑到赛事竞争激烈,赛况多变等因素,本文在FSEC常规模拟工况[13](1C 30 min和2C 30 s)的基础上增设了极限放电状态工况,如表1所示。

表1 模拟FSEC赛事放电工况

同时根据所选电池的具体规格和FSEC大赛规则[12]确定了电池Pack热管理计目标,最高温度≤40 ℃,最大温差≤5 ℃。

1.3 电池Pack散热量计算

镍钴锰酸锂电池属于聚合物锂离子电池,在其内部会有微观粒子间的热传导,在其表面会和空气进行热对流。对流热换遵循牛顿冷却定律[3],电芯内部热传导遵循傅里叶传热定律[14],因此不同放电倍率下的总生热量在一定程度上可等效为系统所需的总散热量,可由式(1)进行确定:

Q总=q总V总

(1)

式中:Q总代表动力电池总产热量,W;q总代表所有单体电池生热速率,W/m3;V总代表所有单体电池体积,m3。

本文研究的是电池瞬态生热问题,故选用Bernardi[15]模型对电池的生热速率模型进行建立,同时考虑到可逆热部分在电池总产热值中占比很小,故所研究电池的生热速率公式简化如下:

(2)

式中:q表示电池生热速率,W/m3;I表示放电电流,A;V表示单体电池体积,m3;R表示电池等效内阻,Ω。

在对电池Pack散热系统设计之前,通过HPPC实验对所研究单体电池的等效内阻进行了探究,经实验得到电池等效内阻和SOC在25℃下的函数关系式如下:

R=0.022 5x5-0.0519x4+0.0326x3+

0.002 9x2-0.007 1x+0.002 4

(3)

式中,x即为SOC。

由Cheng等[16]的研究可知,时间与SOC的关系,如式(4)所示。

(4)

式中:SOCold代表初始电荷状态,为1;I为放电电流,A;CR为单体电池的额定容量,Ah。

联立式(1)—式(4),得到生热速率与放电时间的函数关系式,然后依据此函数关系求得电池Pack在2C倍率放电30 s后所需要的散热量为0.525 kW,在1C倍率放电1 800 s后所需散热量为2.103 kW。

1.4 散热风扇风量的计算

根据不同工况下电池组的产热总量,对风扇的散热量进行计算,由式(5)确定。

(5)

式中:CFM为风扇流量,m3/min;ρ为空气密度,1.29 kg/m3;Cp为空气比热容,1 005 J/(kg·k);Δt为电池箱进出口温差,20 K;出风口温度取为 318 K,进风口温度取为298 K。

经计算2C放电30 s所需风量为1.2 m3/min;1C放电30 min所需风量为4.83 m3/min。对于直径50 mm的进风口,进风速度等效为3 m/s。

1.5 电池Pack散热系统初步设计

结合上述物理参数同时考虑到方程式赛车空间的紧凑性,故将5个模组采用3行2列的形式进行排布,同时设置单体电池间隙1 mm;电池模组纵向间隙2 mm,横向间隙10 mm。除了对模组排布外,还对热管理系统其他电气元器件进行了布置,如图1所示。最终箱体尺寸为544 mm×419 mm×164 mm,进风口和散热风扇均设置了1个,箱体背面的出气口设计为6个。

2 电池Pack散热系统初步热仿真

为了分析初始设计的热管理系统的散热能力和存在的问题,对电池Pack在各个工况下的温度变化情况进行仿真研究。

2.1 模型建立与网格划分

对初始设计的散热系统的结构进行必要简化,如图2所示。将简化后的模型在Design Modeler中划分为电池固体区域和箱体空气区域2个 部分,并设置1个进气口和6个出气口。

将处理好的模型更新至Mesh中,对模型进出口流体复杂处采用局部加密,同时在壁面处设置1 mm厚膨胀层。加密后划分的网格总数为 2 857 496,节点数量为778 298个,网格平均正交质量0.63,平均偏斜度为0.26,最小斜度为0.049,均满足要求。

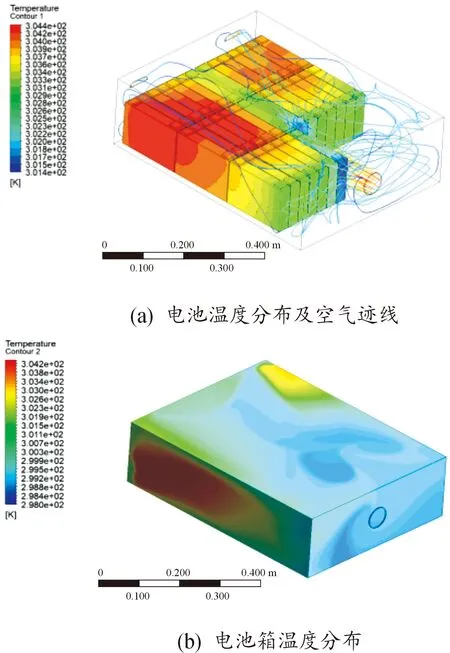
图2 电池Pack在“1C 30 min”工况下仿真结果

2.2 边界条件的设置及求解

根据所研究电池的热物性规格参数,在Fluent中设置电池的等效密度ρ为2 218 kg/m3;比热容cp为1 060 J/(kg·K);等效导热系数λx、λy、λz分别为23.4、5.3、17.4 W/(m·K)。根据式 (1)—式(4)对各个工况下的UDF文件进行编译。将各个工况下的UDF文件加载到电池cell热源中,设置环境温度为25 ℃,进风速度为3 m/s,出口表压为0。设置完成,开始计算。25 ℃下,2C放电倍率时的UDF编译程序如下:

#include"udf.h"

DEFINE_SOURCE(heat_source,cell,thread,dS,eqn)

{

real x,R;

real source,t;

t = RP_Get_Real("flow-time");

x = 1-1*t/1800;

R = 0.0024+0.0225*x*x*x*x*x-

0.0519*x*x*x*x+0.0326*x*x*x

+0.0029*x*x-0.0071*x;

source=10000*R/0.0003915;

dS[eqn] = 0;

return source;

}

2.3 初步热仿真结果分析

通过对电池Pack在1C 30 min、2C 30 s、2C 30 min、3C 40s 4种放电工况下的仿真计算得到电池在各个工况下的温度变化情况,如表2所示。

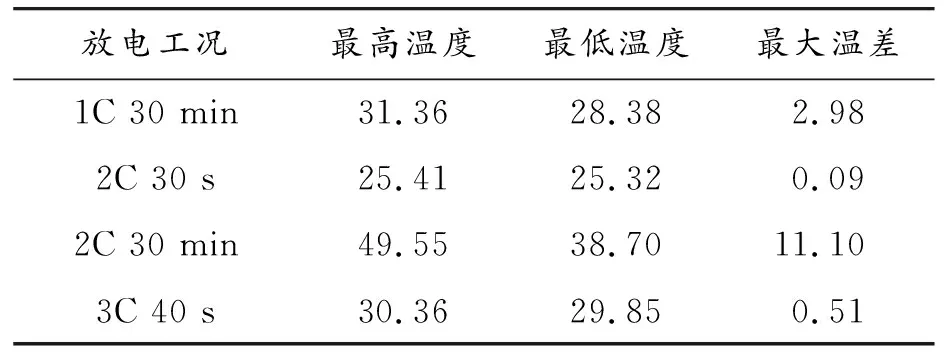
表2 初始散热系统在FSEC 4种放电工况下的热仿真结果 ℃

由结果知,电池包在1C 30min和2C 30 min 2种长时间工况下,温升和温差变化较为明显,故对以上2种工况下的温度场进行详细的对比分析。

2.3.1“1C 30 min”放电工况

从图2可知,当电池Pack以1C放电30 min后,整个电池包最高温度达31.36 ℃,最大温差为2.98 ℃,通过图3(a)可知,在风扇的作用下,电池包各处的温度均有不同程度的下降。在电池箱进风口处和进风口所正对着的纵向位置处的温度明显比电池包左后方和右后方处的温度低,且在电池包左后方,热量有明显的聚集。

2.3.2“2C 30 min”放电工况

当以2C放电30 min后,箱体最高温度达到了49.55 ℃,箱体内最大温差为11.1 ℃,且单体电池的最大温差也将近6 ℃,均超过了所设定的热管理目标值,故初始散热系统在该工况下不达标。

综上分析,初步设计的散热系统在FSEC赛事工况下能起到一定的散热作用,但不能完全达标,尤其是在长时间极限放电工况下,热量积累很明显,无论是最高温度还是温度均一性,都存在显著的问题,同时进出风口位置、风速大小、电池间隙等因素均会对电池箱散热效果产生一定的影响。

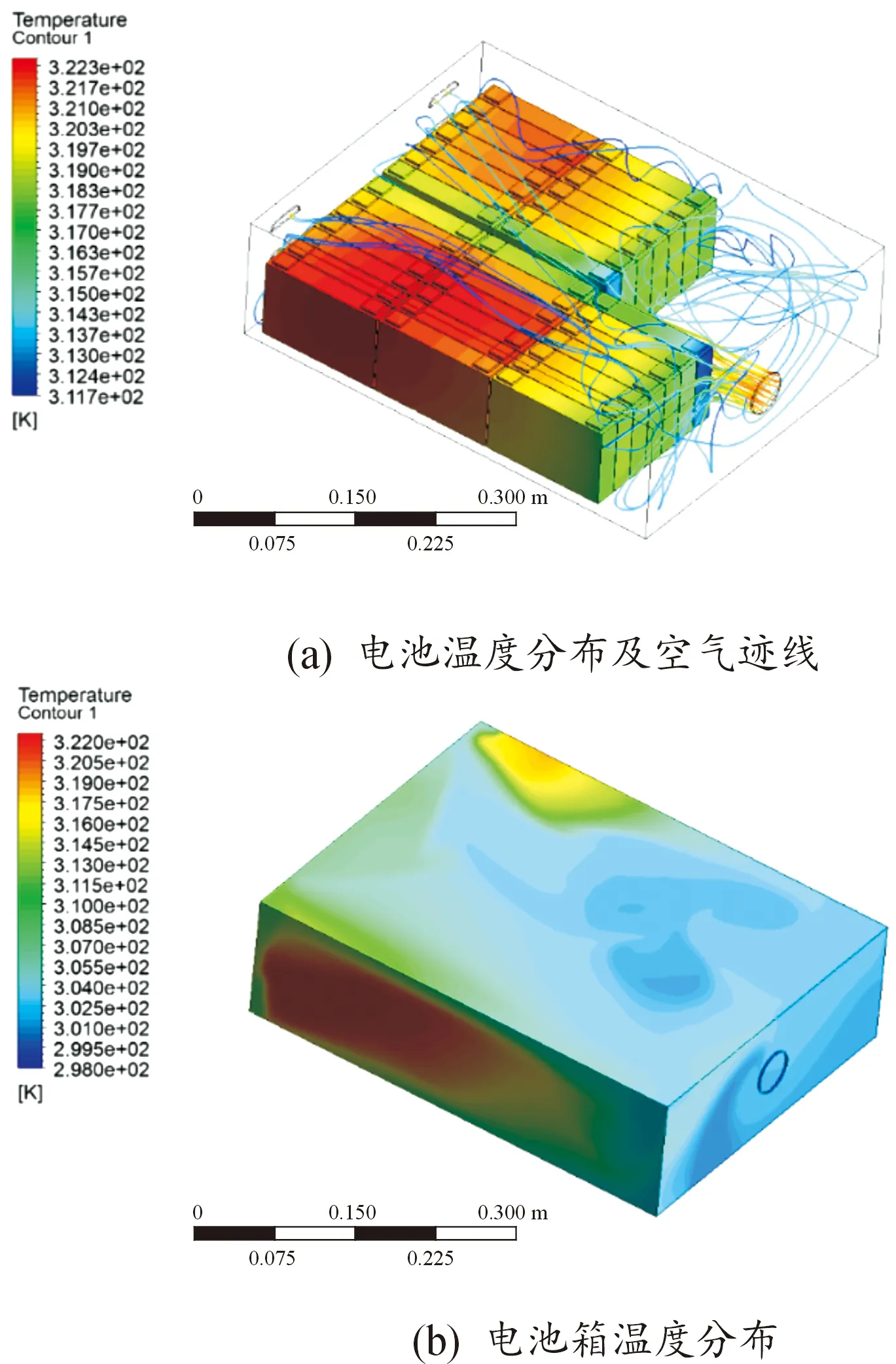
图3 电池Pack在“2C 30min”工况下仿真结果

3 电池Pack散热优化方案探究

通过上述分析影响散热效果的因素较多,故采用正交试验法对电池包散热系统进行优化改进[17]。

3.1 正交试验方案设计

结合初步仿真的结果,挑选进风速度(A)、进风口个数(B)、出风口格栅数(C)、进风口直径(D)、出风口格栅高度(E)、单体电池间隙(F)、模组间隙(G)7个变量作为考量因素,每个因素选取3个水平。查阅正交表规格,选定L18(37)型标准正交表并将最高温度、最低温度及最大温差作为评价指标,如表3所示。

根据表3给出的每个因素的具体水平参数值,按照L18(37)型标准正交表,对本次正交试验的具体方案进行设计,如表4所示。

表3 电池Pack散热仿真方案因素-水平表

表4 电池Pack散热仿真试验方案

3.2 正交试验与结果分析

为了能够直观地查看电池系统的温度分布,所有实验均基于“3C 40s”放电工况进行仿真计算。

3.2.1“最高温度”指标下的结果分析

经计算18组试验在“最高温度”这一指标下的仿真结果,如图4所示。对仿真结果做趋势分析,研究7个因素中三水平的变化对散热系统的影响,找到各个因素在同一水平下的极值,如图5所示。根据仿真结果和极差结果,可知在“最高温度”这一指标下,7个因素对散热系统影响的主次顺序为:B>D>A>F>C>G>E。

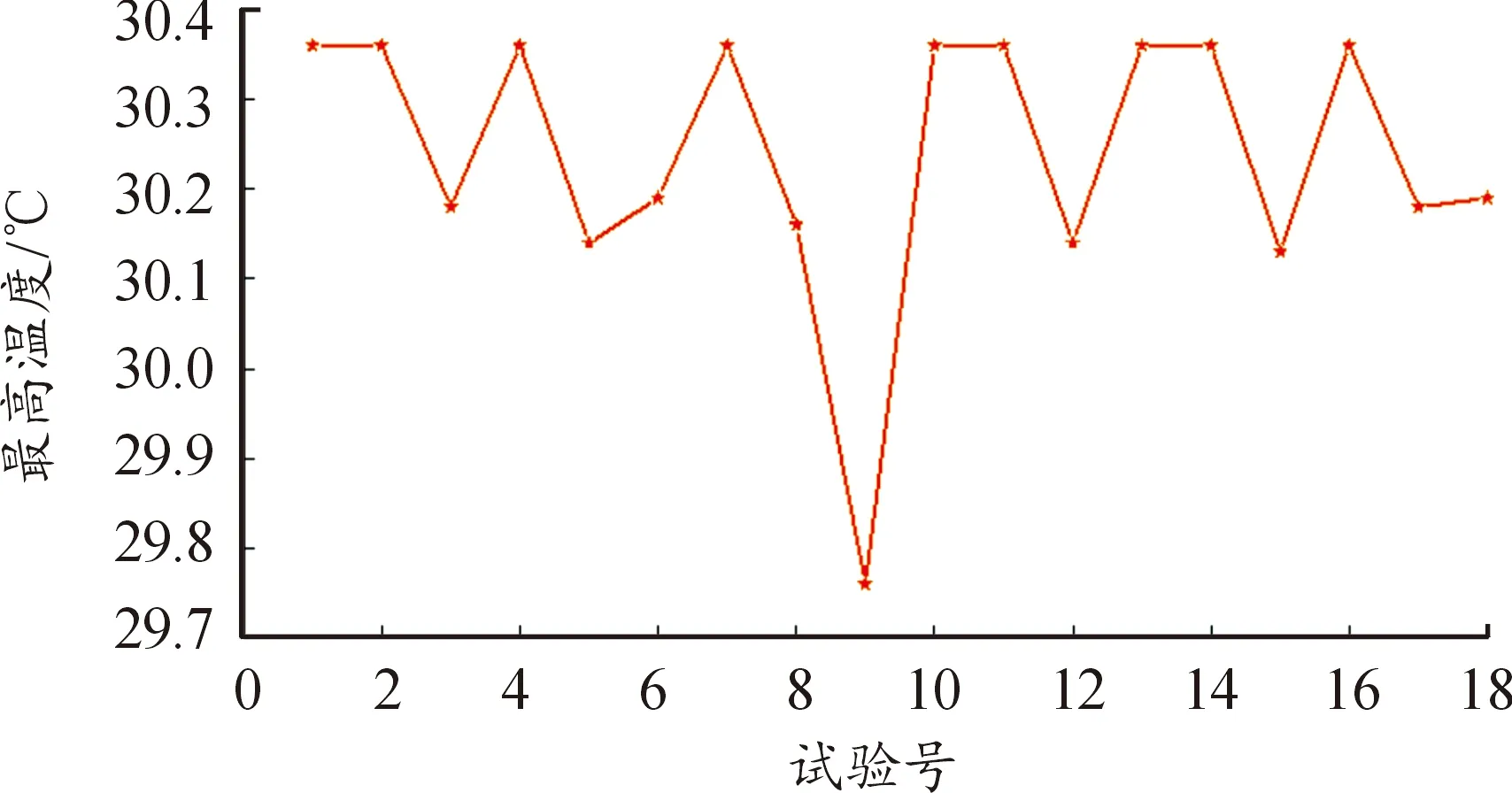
图4 最高温度仿真结果

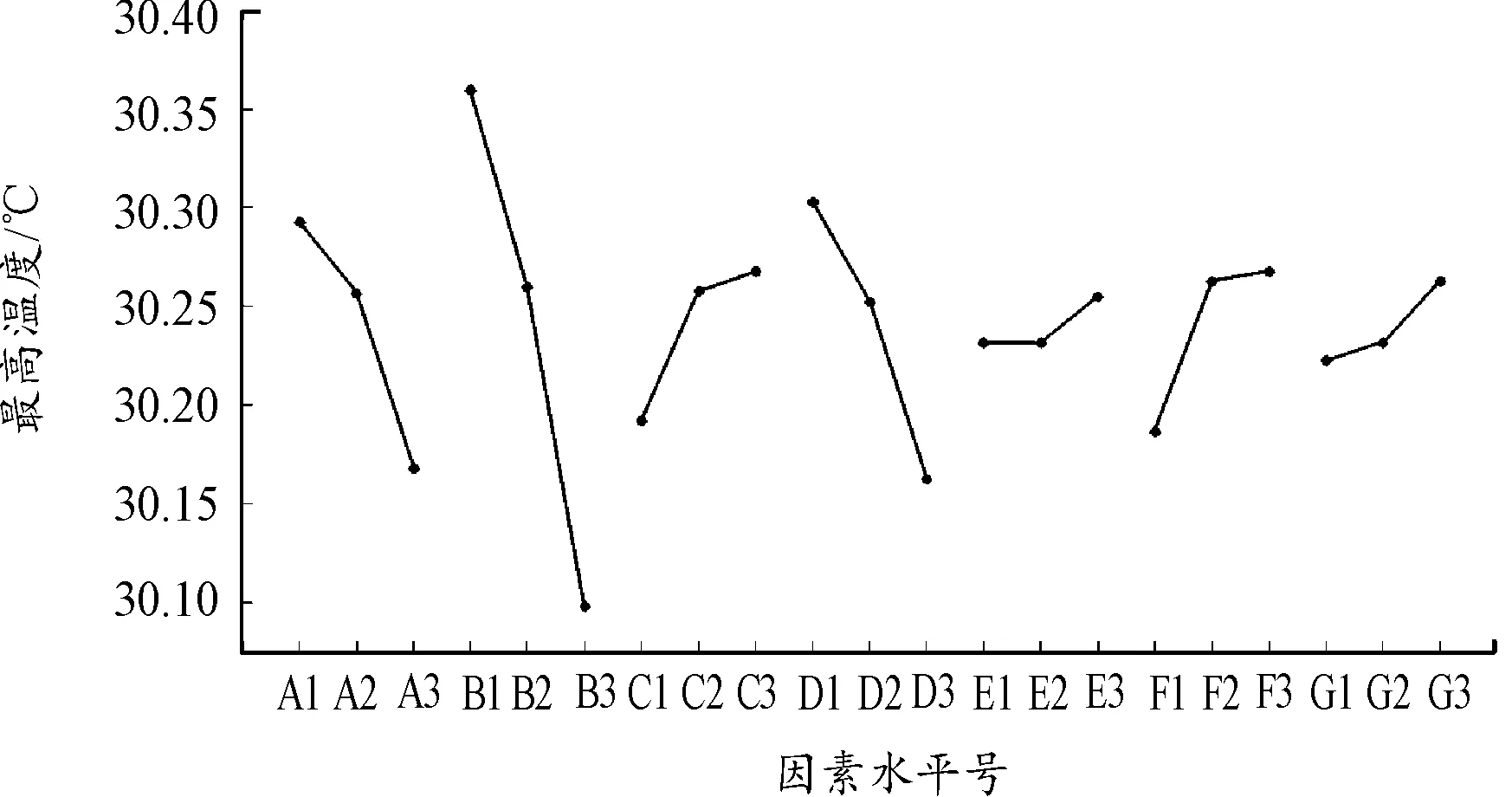
图5 最高温度效应曲线

观察图5可知,因素B(进风口个数)波动范围较大,其次是因素D(进风口直径)。对于散热而言,最高温度越小越好,可知最优方案应该是:B3D3A3F1C1G1E2。

3.2.2最低温度指标

最低温度指标下的仿真结果如图6所示。

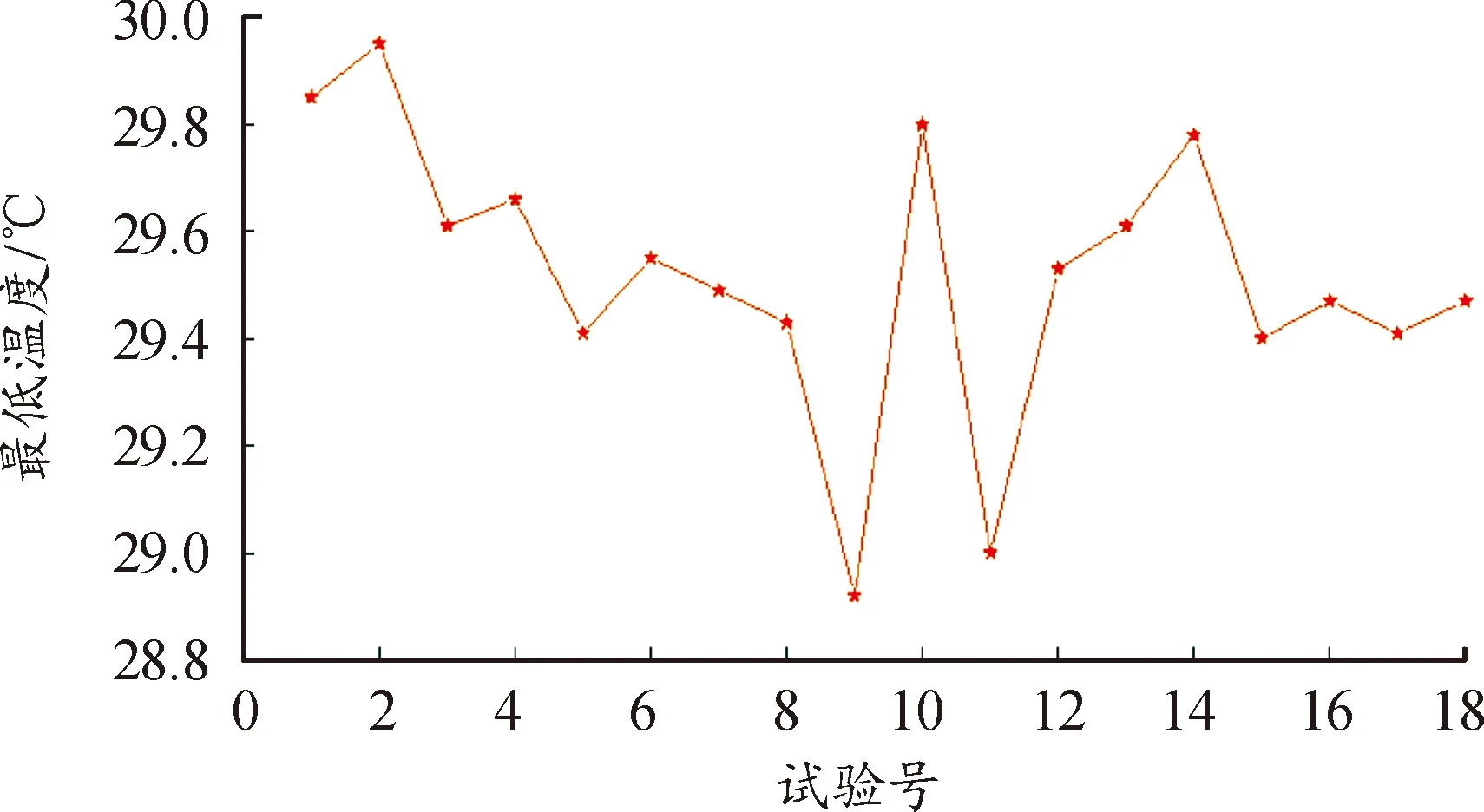
图6 最低温度仿真结果

对仿真结果做趋势分析,如图7所示。根据仿真结果和极差结果,可知道在“最低温度”这一指标下,7个因素的主次顺序为:A>C>B>E>G>F>D。

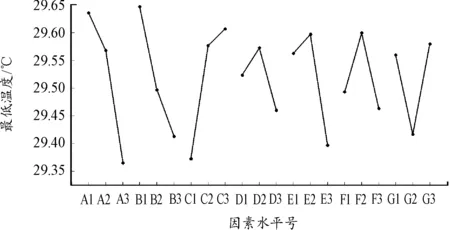
图7 最低温度效应曲线

对于散热而言,最低温度在合理范围内越小越好,由图7可知最优方案应该是A3C1B3E3G2F3D3。

3.2.3最大温差指标

最大温差指标下的仿真结果如图8所示。

图8 最大温差仿真结果

对仿真结果做趋势分析,得到的最大温差效应曲线如图9所示。根据仿真结果和极差结果,可知道在“最大温差”这一指标下,7个因素的主次顺序为:E>C>G>F>A>D>B。

图9 最大温差效应曲线

对于散热而言,最大温差数值越小,温度分布越均一,散热效果越好。由图9可知,最优方案应该是E2C3G1F2A1D2B3。

综上在最高温度、最低温度和最大温差3个评价指标下的最优散热方案分别为B3D3A3F1C1G1E2、A3C1B3E3G2F3D3、E2C3G1F2A1D2B3。

3.3 电池Pack最优散热方案的确定

为了在上述3种方案中遴选出最优散热方案,需要继续从电池组最高温度、最低温度和最大温差3个方面出发,对3种方案的散热指标进行对比分析,如表5所示。

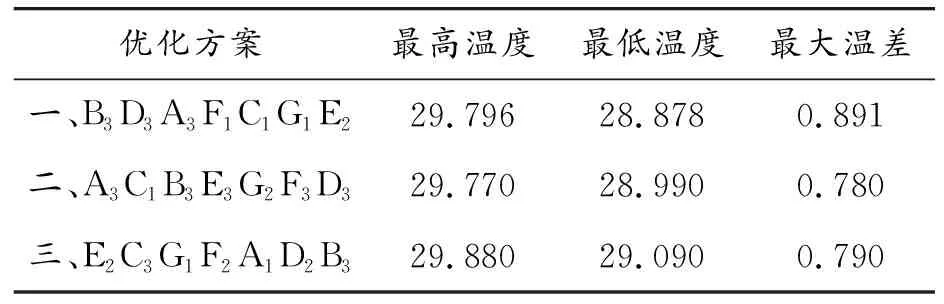
表5 正交试验后的3种优化方案结果 ℃

根据上述热仿真数据结果可知,3种方案的最高温度和最低温度在数值上区别并不明显,而在最大温差方面方案2和方案3明显要优于方案1,故淘汰方案1。因方案2和方案3的三大指标在数值差异并不明显,故需要从温度分布的均一性和电池箱体热量聚集情况两方面出发对最优方案进行遴选。方案2和方案3的电池及电池箱的温度分布情况如图10、11所示。

图10 电池温度分布

由图10可知,方案2和方案3下的电池包高温和低温分布位置大致相仿,但是方案2的温度分布更均匀一些,而且通过图11可知方案3的电池箱整体温度要较方案2要高,且方案3下的电池箱体有明显的热量堆积情况,故方案2的散热情况更理想一些。综上,从散热评价指标、温度均布情况、热量聚集情况三方面综合考虑,确定最优散热方案为A3C1B3E3G2F3D3。

4 电池Pack散热系统优化效果分析

4.1 优化后的散热方案可行性验证

为了验证优化后散热系统的散热能力和优化效果,本节按照优化后的散热方案对电池Pack在FSEC赛事4种工下的温度变化情况进行仿真计算和实车试验。

4.1.1仿真计算

根据优化后的散热方案对电池散热系统重新建模,并对电池Pack在4种工况下的温升情况进行仿真计算及整理统计,如表6所示。

表6 优化后散热系统在FSEC 4种放电工况下的仿真结果 ℃

由表6可知优化后的散热系统在上述4种放工况下,温升和温差变化均在理想变化范围内,均满足设计目标要求。当电池在长时间极限工况(2C 30 min)下放电时,最高温度为33.37 ℃,相对初始散热系统在同样工况下的49.55 ℃,优化了32.65%,优化效果明显。

4.1.2实车试验

根据最优散热方案,对电池散热系统的各零部件进行设计加工及装配,如图12所示,并根据图12对温度传感器进行布置,图13传感器P1-P7位置是根据仿真条件下最高温和最低温出现的位置进行确定的,为的是更为准确地测量电池包的最高和最低温度。

图12 电池箱及电动赛车实物

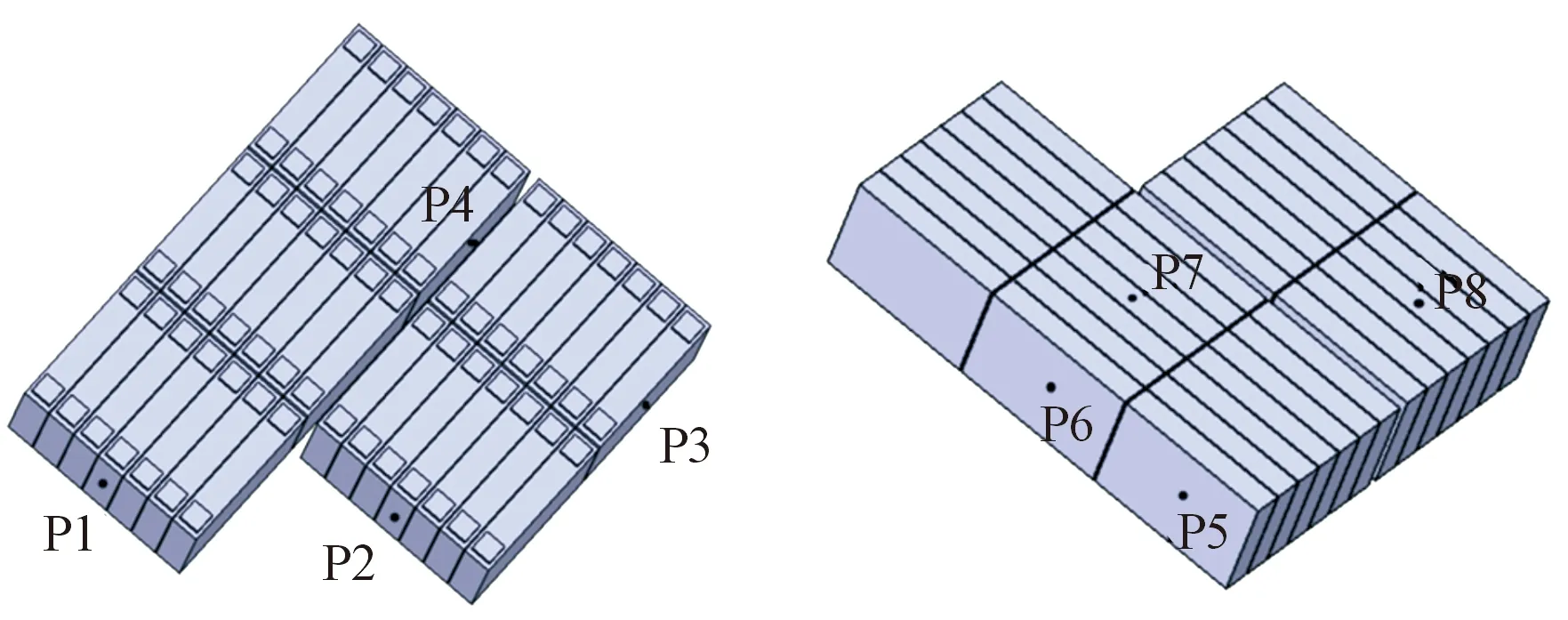
图13 温度传感器布置位置

将制作完成的电池箱安装在电动方程式赛车上,根据FSEC大赛规则和实际竞赛工况,对测试路径及跑动工况进行设计。在风速小于3 m/s,温度为25 ℃的环境下,由2名赛车手分别完成加速工况1(直线加速30 s)和耐久工况2(耐久行驶30 min)2个跑动项目。

两车手测试前,赛车电量保证足够且相等,每个项目跑动间隔要大于30 min。将两车手跑动测试的结果取平均值并与仿真结果对比分析,如图14 和图15所示。

由图14和15可知,在直线加速30 s实车测试后电池包的最高温度27.06 ℃,最大温差0.477 ℃,在耐久行驶30 min后电池包的最高温度30.2 ℃,最大温差2.1 ℃,以上数据均在设定的目标温度范围之内,故优化后的散热系统在实际竞赛过程中能够满足散热要求。同时在直线加速30 s工况下试验和仿真的最大温差不超过2 ℃,误差保持在7.39%之内;在耐久行驶30 min工况下试验和仿真的最大温差不超过2.82 ℃,误差保持在9.34%之内。

综上2种工况下试验和仿真误差均在允许范围内,且各工况下试验和仿真条件下的温度变化趋势基本一致,故优化后的散热系统在实际赛事工况下应用是可行的,且本研究的仿真结果较为准确。

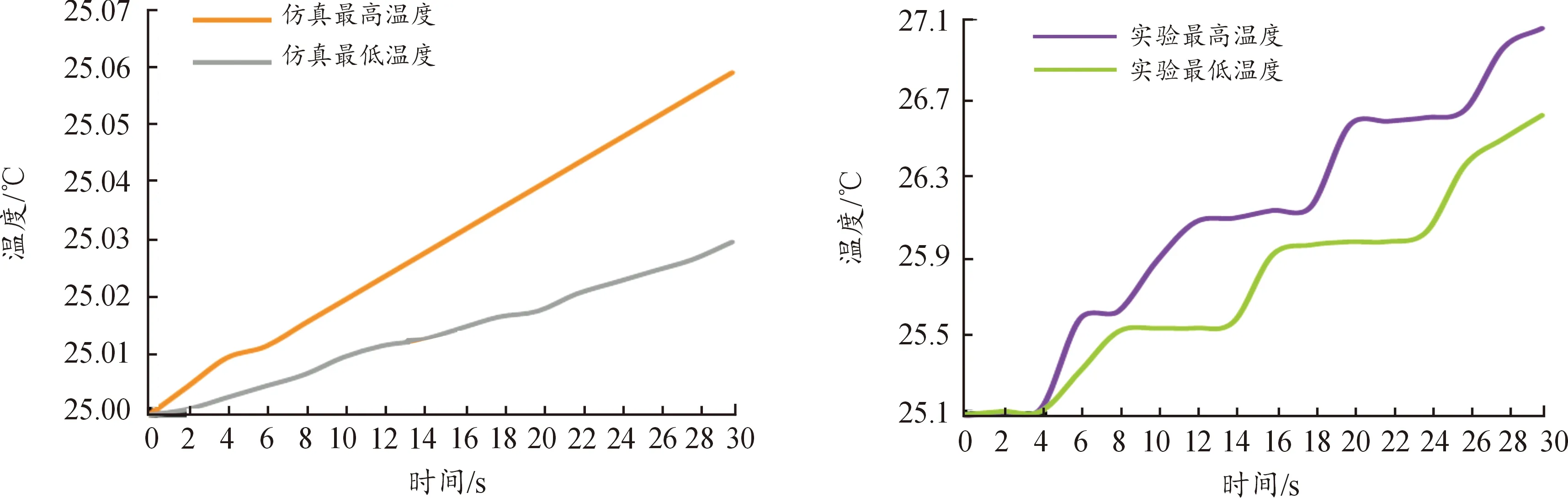
图14 加速工况一(2C 30 s)仿真和试验温度值

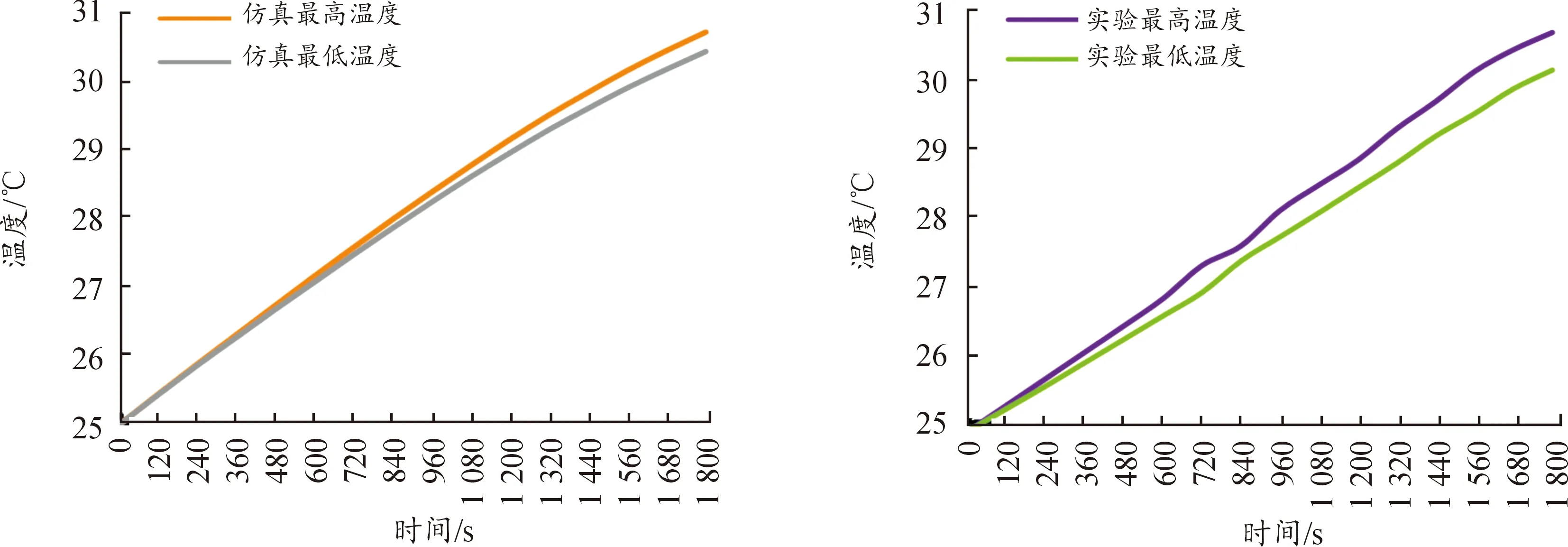
图15 耐久工况二(1C 30 min)仿真和试验温度值

4.2 电池Pack散热系统优化效果

4.2.1电池整体温升和温差方面

基于正常放电状态下的2种工况(1C 30 min和2C 30 s)对优化前后的电池温度场云图进行对比分析,如图16和图17所示。

图17 2C 30 s 工况下优化前后电池温度变化云图

当电池包在1C 30 min工况下,由图16可明显看出优化前的电池包温度在前后2部分温差较大,且电池包整体温度较高,最高温度为31.36 ℃,较环境温度升高了6.36 ℃;而优化后的电池包整体温度较低,最高温度仅为26.63 ℃,较环境温度升高了1.63 ℃,整体温控效果较好。经计算电池散热系统在优化前后在最高温度和最大温差方面分别优化了15.08%和86.58%,有较为明显的优化效果。

当电池组在2C倍率下放电30 s后,由图17可以看出优化前和优化后的电池包的整体温度均不高,温升和温差的变化均不超过1 ℃,但是对比发现,优化后电池包的温度分布更加均匀,并没有出现大面积的热量聚集。经计算,优化后的散热系统在最高温度和最大温差方面分别优化了1.38%和66.67%,故在该工况下电池包温度分布的均一性得到了较好的改善。

4.2.2散热系统内空气迹线分布方面

基于“1C 30 min”工况,对优化前后散热系统内的空气迹线图进行对比分析,如图18所示。

优化前电池箱进风口单一且空气流量较小,冷却空气主要流经电池箱中间位置,在电池箱两侧和单体电池缝隙之间流过的冷却空气很少,电池温度整体较高,散热效果不佳,且在电池箱后部左右2个位置有明显的热量堆积,电池温度均一性较差;优化后的散热系统增加了进风口数量,同时对进风口的位置进行了均布调整,在布置上更有利于冷却空气均匀流向整个电池包组,同时对电池单体和模组间的间隙进行了合理调整,从迹线图可看出在整个放电过程中电池箱内的冷却空气分布比较均匀,即使在持续放电30 min后也并未出现大面积的热量聚集,且温度仅升高了1.63 ℃,综上,优化后的电池热管理系统在结构上布置更为合理,冷却空气在电池箱的分布更加均匀,该结构下的散热系统有较好的温控散热能力。

5 结论

针对所研究的动力锂离子电池的散热系统主要做了4方面的工作。一是基于FSEC赛车电池包组的相关参数,对电池Pack的散热系统进行了初步设计;二是通过CFD仿真的方法对初始散热系统的散热能力及影响因素进行分析研究;三是利用正交试验法,以最高温度和温差最小化作为优化目标,同时结合电池温度分布的均一性和电池箱的热量聚集情况等对最优散热方案进行遴选,相对全面试验法,减少了试验次数,提高了优化效率;四是通过实车跑动试验和CFD仿真相结合的方式,验证了所设计方案在FSEC赛事中应用的可行性且有较好的优化效果,温差最大优化率可达86.58%,证实了本研究的仿真结果较为准确可靠。

在正交试验遴选最优方案以及对优化效果进行对比分析过程中,在考虑最高温度、最低温度和最大温差三大目标因素的同时,充分考虑了电池包温度的均布性和电池箱体热量的聚集情况,不仅使最优方案的遴选过程更加高效,而且在散热效果分析方面更加有据可依。故在处理动态仿真优化问题方面,在选取结果性优化目标的同时,增加一些对试验过程有影响因素作为辅助参照,可能会使优化效果更为理想。

本研究在探究过程中以散热效果最优为最终目标,并未考虑能耗问题。故日后在本研究的基础上可以从散热和能耗相均衡的角度出发,对风冷散热系统进行更深一步的研究。