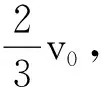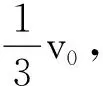对一道经典碰撞习题解析的修正

周洪松

(秦皇岛市第一中学 河北 秦皇岛 066006)

1 原题及解析

如图1所示,水平地面上A、B两个木块用轻弹簧连接在一起,质量分别为2m、3m,静止时弹簧恰好处于原长.一质量为m的木块C以速度v0水平向右运动并与木块A相撞.不计一切摩擦,弹簧始终处于弹性限度内,则碰后弹簧的最大弹性势能不可能为( )

图1 原题题图

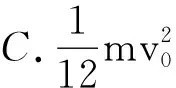
解析:当C与A发生弹性正碰时,根据动量守恒定律和能量守恒定律有

mv0=mv1+2mv2

联立解得

当A、B速度相等时弹簧的弹性势能最大,设共同速度为v3,以A的初速度方向为正方向,则由动量守恒定律得

2mv2=(2m+3m)v3

由机械能守恒定律可知

解得

当C与A发生完全非弹性正碰时,根据动量守恒定

律有

mv0=3mv4

当A、B、C速度相等时弹簧的弹性势能最大,设共同速度为v5,则由动量守恒定律得

3mv4=6mv5

由机械能守恒定律可知

解得

由此可见,碰后弹簧的最大弹性势能范围是

2 对原题解析的修正

上述解析中认为C与A碰撞过程中发生弹性碰撞没有机械能损失,弹簧的弹性势能最大;C与A发生完全非弹性碰撞损失机械能最大,弹簧的弹性势能最小.但是C与A发生完全非弹性碰撞后弹簧的弹性势能就一定是最小的吗?假设两个质点碰撞过程中总动能没有损失,则满足动量和能量守恒定律

m1v1+m2v2=m1v′1+m2v′2

联立解得

为了区别碰撞的性质引入恢复系数e,定义为分离速度和接近速度的比值

则解可以化为

完全弹性碰撞中e=1,完全非弹性碰撞中e=0,当0

本题中m1=m、m2=2m、v2=0、v1=v0,代入上式得A的速度满足

弹簧的弹性势能趋近于

综上所述碰后弹簧的最大弹性势能范围是