基于深度强化学习的柔性作业车间调度方法*
2023-12-11崔雪艳万烂军赵昊鑫李长云
崔雪艳 万烂军 赵昊鑫 李长云
(①湖南工业大学计算机学院,湖南 株洲 412007;②智能信息感知及处理技术湖南省重点实验室,湖南 株洲 412007)
生产调度在制造系统中起着至关重要的作用,有效的调度方案是提高生产效率和提高资源利用率的重要因素。柔性作业车间调度(flexible job shop scheduling,FJSP)问题[1]中每道工序可在多个机台上处理,每个机台可处理多道工序。在FJSP 中,机台的柔性引入更符合制造系统的实际情况,能够提高制造系统的生产效率,但扩大了可行解的范围,进而增加了生产调度的难度和复杂性。
近年来,众多学者已对FJSP 展开了广泛的研究。启发式调度规则[2]可对动态事件做出即时响应,但由于不同调度环境会对调度性能产生影响,因此很难保证找到最优调度方案。元启发式算法通常通过进化算子或粒子运动来迭代地搜索调度方案[3],用于求解FJSP 的元启发式算法主要包括遗传算法[4-7]、粒子群优化[8-9]、人工蜂群[10-11]、鲸鱼优化算法[12-13]以及灰狼算法[14-15]等。Chen N L 等[6]针对具有不确定加工时间的FJSP,提出了一种精英遗传算法。Li Y B 等[11]提出了一种改进的人工蜂群算法来求解FJSP,该算法采用三维编码/解码机制和动态邻域搜索提升了算法的性能。Liu Z F 等[8]提出了一种可变邻域的混合遗传粒子群算法来求解FJSP,将粒子群作为遗传算法的变异算子有效地提升了收敛速度。Yang W Q 等[12]提出了一种混合鲸鱼算法来求解FJSP,其中使用种群多样性机制来确保种群多样性在迭代过程中保持稳定。为了解决FJSP,李宝帅和叶春明[13]提出了一种混合正余弦鲸鱼优化算法。Li X Y 等[14]提出了一种改进的灰狼优化算法来求解分布式FJSP,该算法设计了4 个交叉算子来拓展搜索空间。Lin C R 等[15]提出了一种基于学习的灰狼优化算法来求解具有额外资源和机台准备时间的随机柔性作业车间调度问题。
这些元启发式算法虽然可以获得高质量的调度方案,但当问题规模增大时,求解FJSP 的计算时间迅速增长,导致其难以满足快速调度的需求。此外,一旦问题结构发生变化,需重新调整算法参数。而深度强化学习结合了深度学习的感知能力和强化学习的决策能力,在求解车间调度问题方面具有很大的潜力。因此,本文提出了一种有效求解FJSP的深度演员评论家强化学习方法,并采用不同规模的基准实例对该方法进行了验证。
1 基本理论
强化学习通过智能体与环境的交互,学习从环境状态到行为的映射,从而获得最大的奖励。强化学习的模型框架如图1 所示。在t时刻,从环境中获取当前的状态,智能体在动作空间中选出一个动作,执行动作后,状态更新为下一状态,同时环境给出奖励。
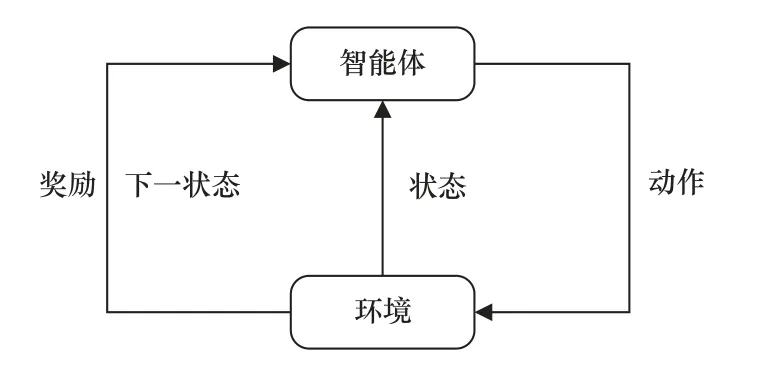
图1 强化学习的模型框架
2 FJSP 转化
2.1 问题定义
FJSP 描述如下:在m台机台M={M1,M2,···,Mm}上可加工n个工件 J={J1,J2,···,Jn}。每个工件Ji由p道连续的工序组成,每道工序Oi,j都可在匹配的机器Mi,j⊆ M 上进行加工,其中Oi,j表示工件Ji的第j道工序,Pi,j,k表示Oi,j在机台Mk上的加工时间。Si,j和Ei,j为工序Oi,j的开始时间和结束时间,Ct为调度t步后FJSP 实例的最大完工时间。
为了简化问题,需满足以下约束条件:每个机台一次只能加工一道工序;每个工件都由一个固定的工序序列组成;工序只能在指定的机台上加工;工序在不同的机台上加工,加工时间可能不同;一旦在机台上开始了一个操作,就不能中断;不考虑机台之间的运输时间。
本文的目标是最小化所有工件的最大完工时间,目标函数为
2.2 问题建模
随着FJSP 规模的增加,单个智能体的集中控制计算复杂度也随之增加,从而导致在解决大规模FJSP 时适应性较差。为了解决这一问题,将FJSP建模为一个多智能体马尔科夫决策过程,其中,将机台视为智能体,并对多智能体马尔科夫决策过程中的状态空间、动作空间以及奖励函数进行设计。
状态空间描述了机台智能体在不同时间的生产加工场景信息,具体来说,状态空间包括状态矩阵Sm、机台可加工矩阵Am和工序加工时间矩阵Pm。Sm表示每道工序的调度状态,“0”表示该工序未被调度,“1”表示该工序已被调度。Am表示机台的加工能力,“1”表示该机台可加工该工序,“0”表示该机台不可加工该工序。Pm表示每道工序在不同机台上的加工时间。这3 个矩阵代表了状态的3 个不同通道,作为卷积神经网络的输入。
动作空间包含了智能体可选择的所有动作。由于目标函数是最小化最大完工时间,因此选择了一些与Ji的总工时以及Oi,j的Pi,j,k相关的调度规则作为动作。表1 展示了动作空间包含的8 个简单的调度规则。
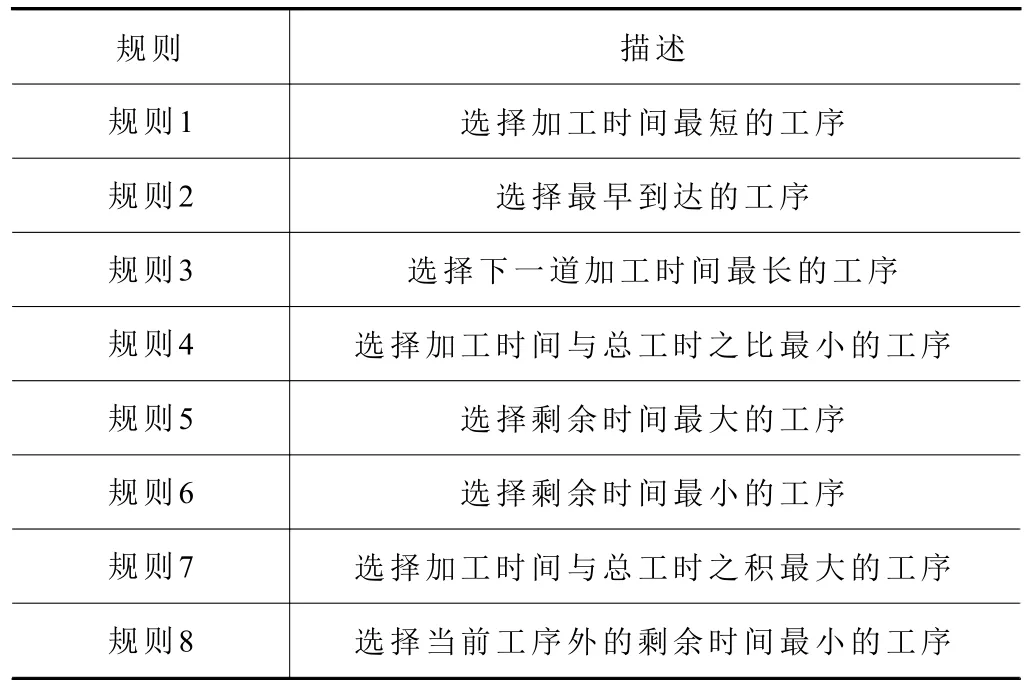
表1 调度规则表
演员网络输出动作at后,机台智能体会根据at对应的调度规则来确定被调度的工序,随后FJSP环境会给予一个即时奖励rt。即时奖励反映了at对调度方案产生的短期影响。即时奖励的计算见式(2)。其中:Ct-1表示当前调度t步的上一步求解FJSP 实例所得的最大完工时间。
3 基于深度强化学习求解FJSP
3.1 网络结构设计
基于深度强化学习求解FJSP 的总体框架如图2所示,在该方法中,构建一个演员评论家(actor critic flexible job shop scheduling,AC-FJSP)模型。其中:演员网络的输入为状态,输出为调度规则。智能体根据输出的调度规则选择合适的工序,当该工序被调度后,环境给出奖励,将状态和奖励输入给评论家网络,评论家网络去评估该调度规则并反馈给演员网络以更好地调整调度策略。

图2 基于深度强化学习求解FJSP 的总体框架
基于深度强化学习的AC-FJSP 模型的网络结构见表2。该模型由2 个卷积层、4 个BN 层、4 个全连接层组成。Conv1 和Conv2 为演员网络与评论家网络共享的卷积层。在Conv1 和Conv2 中,都使用16 个大小为1×1 的卷积核,padding 设置为零填充,以保证卷积后的特征图与输入数据的大小保持一致。在Conv1 和Conv2 后分别采用BN1 和BN2进行二维批归一化处理,可加快网络的训练速度并防止过拟合。FC1、BN3 和FC2 是演员网络的层,用于生成调度策略并输出动作。FC3、BN4 和FC4是评论家网络的层,用于估计状态值函数并输出状态值。FC1、FC2、FC3 和FC4 中都使用100 个神经元。在FC1 和FC3 后分别采用BN3 和BN4 进行一维批归一化处理。此外,在Conv1、Conv2、FC1和FC3 后使用ReLU 激活函数,可增强模型的表达能力。
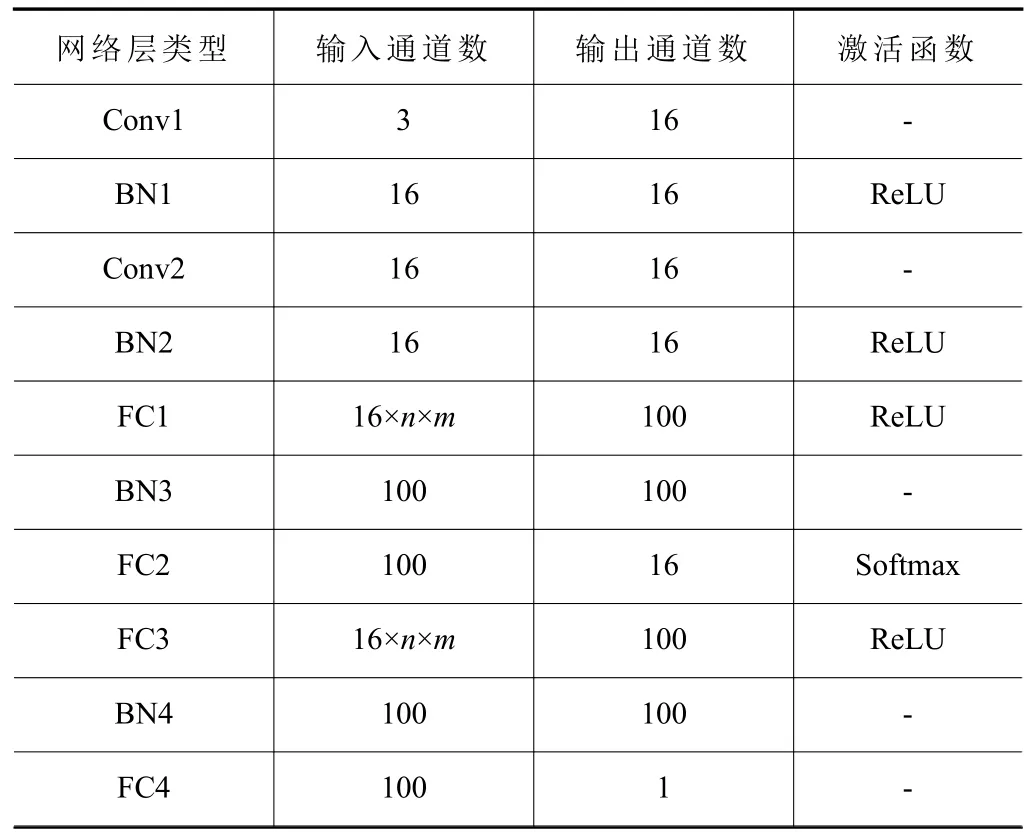
表2 AC-FJSP 模型的网络结构
3.2 模型训练
用于求解FJSP 的AC-FJSP 模型的训练过程,具体步骤如下。
步骤1:确定完整调度次数I、用于模型训练的FJSP 实例、学习率lr。
步骤2:初始化演员网络和评论家网络。
步骤3:根据FJSP 实例构建状态空间中的3 个矩阵Sm、Am和Pm。
步骤4:初始化Sm、Am和Pm。
步骤5:获取可加工工序集合Gset,其中待选的工序Oi,j需满足3 个条件,即Oi,j未被加工、Oi,j的上一道工序Oi,j-1已被加工、Oi,j可被Mk加工。
步骤6:获取当前状态st,演员网络通过Softmax 策略输出动作at。
步骤7:判断Gset是否为空,若是,则即时奖励rt取值为零;若否,根据动作at从Gset中选出符合该调度规则的工序Oi,j。
步骤8:获取每个机台上当前已被加工的最后一道工序的结束时间并取其中的最大值作为当前的最大完工时间。
步骤9:更新下一状态st+1,并根据式(2)计算rt。
步骤10:采用Shared-Adam 优化器进行网络参数的更新。
步骤11:判断当前FJSP 实例的所有工序是否均被调度,若是,结束此次完整调度;否则,重复执行步骤5 至步骤10。
步骤12:重复执行步骤4 至步骤11,直到完成第I次完整调度为止,从而获得训练好的ACFJSP 模型的网络参数,并保存该模型。
4 实验
4.1 实验设置
为验证本文提出的方法求解柔性作业车间调度的有效性,在不同规模的FJSP 实例上进行测试。根据实例的规模大小,分为小规模实例、中规模实例、大规模实例以及超大规模实例4 大组。其中:小规模有10×5、15×5、20×5 和10×10;中规模有10×20、20×10、10×40 和15×15;大规模有20×40、20×60、50×20 和 50×40;超大规模有 50×60、100×20、100×40 和100×60。实例规模为10×5 表示该实例中包含10 个待加工的工件和5 台可加工工件的机台。根据数据来源,分为Hurink J[16]实例和Behnke D[17]实例,加粗体表示求解某实例最佳的最大完工时间。
对比方法:本文提出的方法与加工时间最短(shortest processing time,SPT)、剩余加工时间最长(longest remaining processing time,LRPT)、当前工序的加工时间与总工时之比最小(smallest ratio of processing time to total work,SPT/TW)3 条启发式调度规则,改进遗传算法(improved genetic algorithm,IGA)[4]和混合离散粒子群算法(hybrid discrete particle swarm optimization,HDPSO)[9]进行比较。
完整调度的迭代次数为300 次,学习率为0.005。神经网络的优化器为Share-Adam,其中betas参数设置为0.99,eps参数设置为10-8。
实验平台的硬件配置如下:一个8 核的Intel Core i7-9700K CPU、2560 核NVIDIA GeForce RTX 2070 SUPER GPU 以及64GB 内存。实验平台的软件配置如下:Python 3.7、Pytorch 1.6。
4.2 比较求解质量
为验证AC-FJSP 的有效性,与启发式调度规则、IGA 和HDPSO 比较求解实例的最大完工时间。ACFJSP 相对最优启发式调度规则的优化率Arate的计算式为
AC-FJSP 相对于IGA 和HDPSO 的优化率Brate的计算式为
式中:ZH表示启发式调度规则的最优解,ZA表示AC-FJSP 的解,ZY表示IGA 和HDPSO 的最优解。
表3 展示了启发式调度规则、IGA 和HDPSO求解不同规模的FJSP 实例的最大完工时间。求解10×5、20×5 和10×40 规模实例的最佳调度规则分别是LRPT、SPT/TW 和SPT。由表3 可知,不同规模的FJSP 实例中,启发式调度规则性能不稳定。ACFJSP 求解的结果与启发式调度规则相比较,优化率最高有63.2%,最低也有12.7%。AC-FJSP 求解的结果与IGA 和HDPSO 相比较,求解不同规模FJSP 实例的最大完工时间均相近。上述实验结果表明AC-FJSP 的求解性能稳定且优,泛化性较好。原因在于AC-FJSP 的动作空间包含了多个调度规则,通过训练,AC-FJSP 可自适应地选择合适的调度规则,而不是使用同一个调度规则求解所有的FJSP实例。
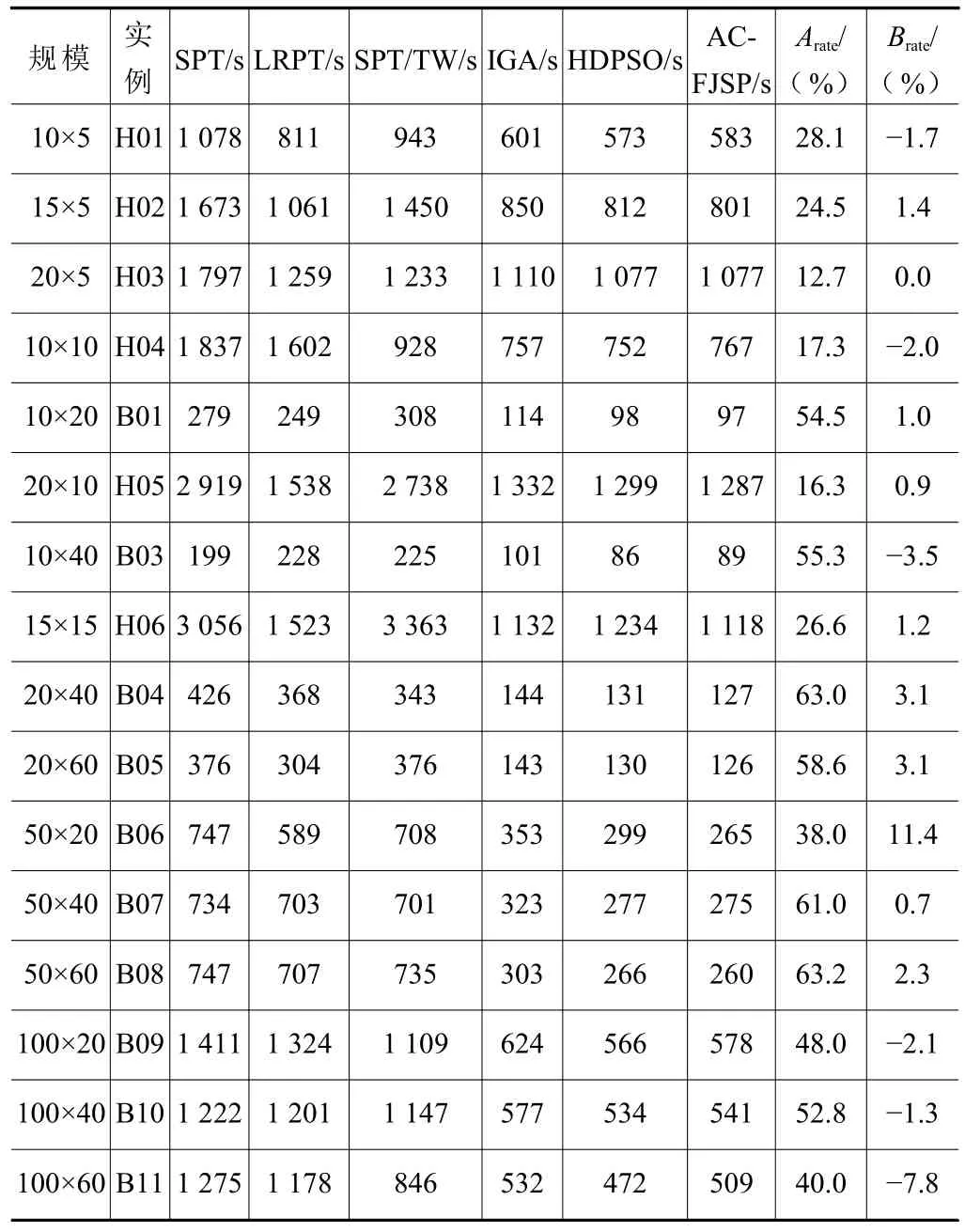
表3 求解FJSP 实例的最大完工时间
4.3 比较求解效率
为进一步验证AC-FJSP 的有效性,与启发式调度规则、IGA 和HDPSO 比较求解效率。AC-FJSP相比启发式调度规则最短计算时间的提升率Crate的计算式为
AC-FJSP 相对于IGA 和HDPSO 的最短计算时间的提升率Drate计算式为
式中:TH为启发式调度规则的最短计算时间;TA为AC-FJSP 的计算时间;TY为IGA 和HDPSO 的最短计算时间。
表4 展示了启发式调度规则、IGA 和HDPSO求解不同规模的FJSP 实例的计算时间。启发式调度规则和AC-FJSP 在求解小规模和中规模FJSP 实例的计算时间均在8 s 内,求解大规模实例的计算时间均在110 s 内。图3 所示为求解超大规模FJSP实例的执行时间。就算求解超大规模的实例,ACFJSP 的计算时间也与启发式调度规则的计算时间相接近。与IGA 和HDPSO 相比较,AC-FJSP 的计算时间的提升率最高有98.1%,在求解超大规模实例时提升率最低也有60.3%。原因在于演员评论家算法可进行单步更新,提高了学习效率。当训练完成后,模型已经学习到最优的参数,可快速地进行调度,从而缩短了计算时间。AC-FJSP 利用大规模实例进行训练,其他实例可利用该模型在较短的时间内得到一个较好的调度方案。
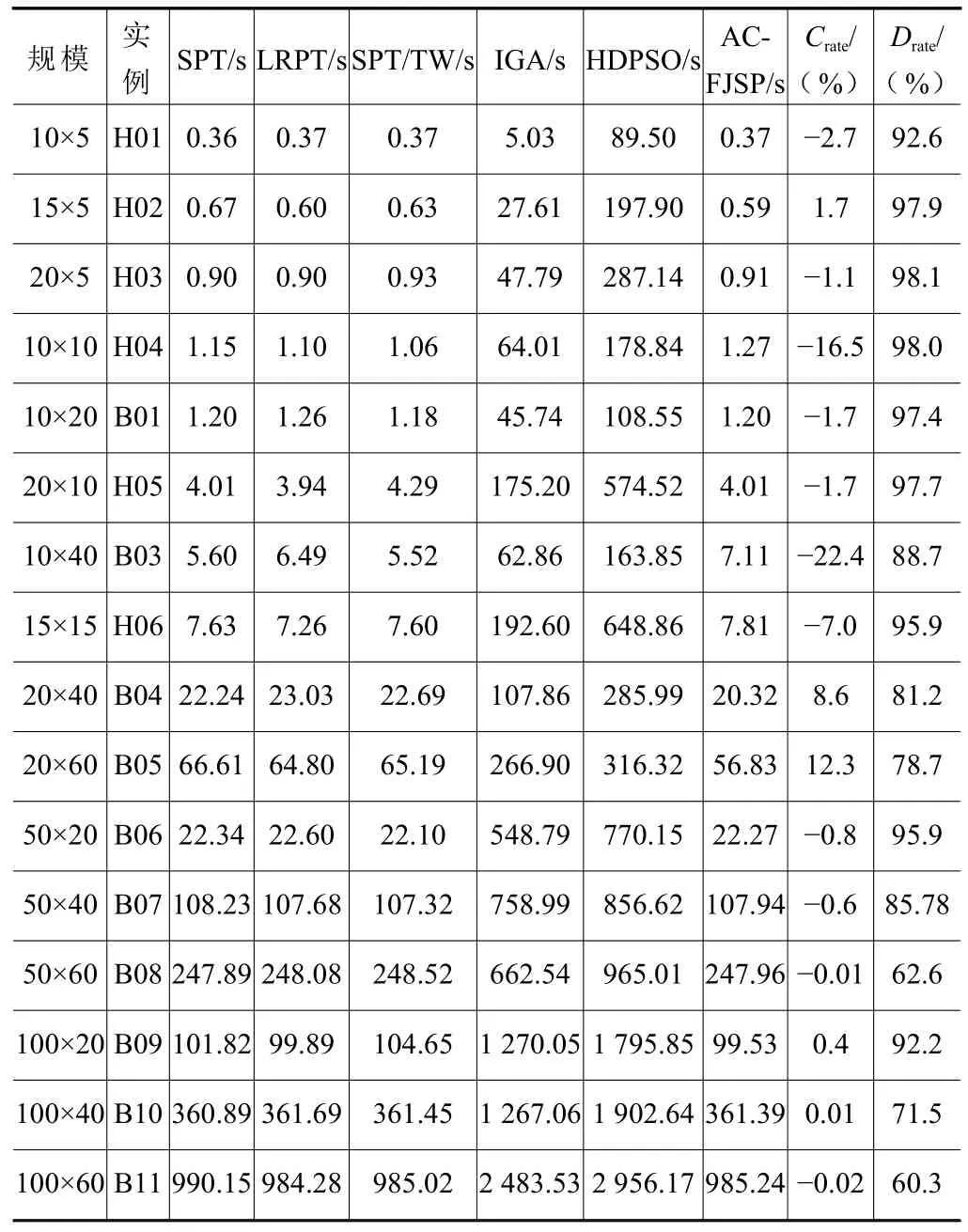
表4 求解FJSP 实例的计算时间
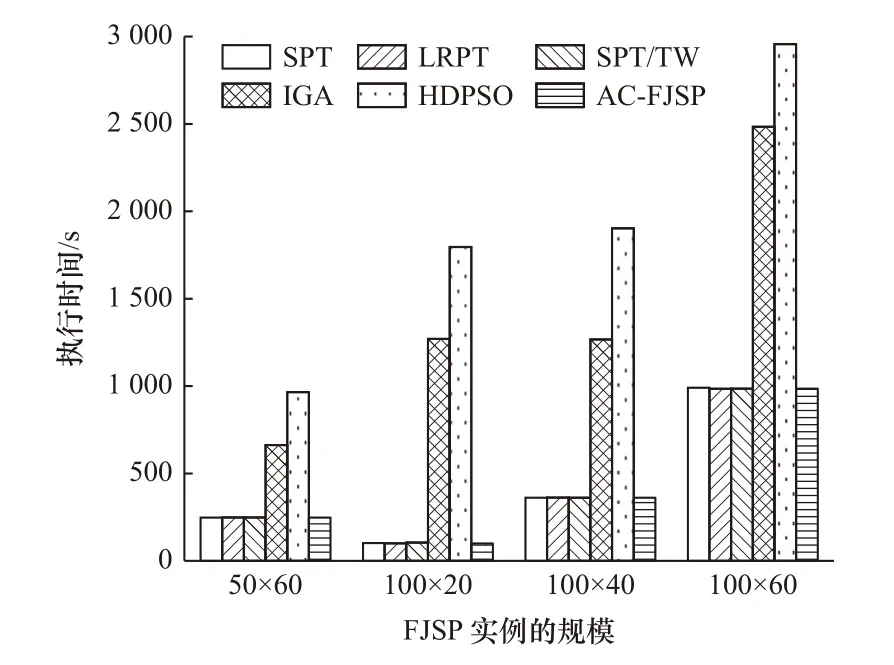
图3 求解超大规模FJSP 实例的执行时间
5 结语
本文提出了一种有效求解大规模柔性作业车间调度问题的深度强化学习方法,以最小化最大完工时间为优化目标构建了一个AC-FJSP 模型,机台智能体根据演员网络输出的调度规则选择合适的工序进行调度。为验证提出方法的有效性,采用启发式调度规则、IGA、HDPSO 和提出的方法开展一系列对比实验。结果表明提出的方法在求解质量方面优于启发式调度规则,在求解效率方面优于元启发式算法。
在实际工业生产中可能存在机器故障和紧急插单等动态事件。TD3 算法具有强大的学习能力和稳定性,适合处理连续动作空间的问题。因此,下一步将采用TD3 算法来求解动态柔性作业车间调度问题。
