基于混合优化算法的船用柴油机脉动装配线平衡优化技术研究*
2023-12-11张胜文陈银娟
陶 帅 张胜文 陈银娟 王 沾 章 振
(江苏科技大学机械工程学院,江苏 镇江 212003)
装配阶段是产品全生命周期中最重要、耗费大量资源与时间的步骤之一,其中,复杂产品的装配过程需要占用整个生产过程中约33%的人力资源、40%以上的生产费用以及40%~60%的总生产工时[1]。装配线平衡是通过合理的任务分配,确保各工作站的工作负荷相对均衡,以此来提高效率和资源利用率、缩短装配周期和降低生产成本。目前,针对装配线平衡问题,许多研究人员已经进行了大量研究。Uğur Ö等[2]考虑并行装配线中工人分配和装配线平衡问题联合周期时间最小化的研究,建立二元线性数学规划模型,并提出了一种基于人工蜂群的大中型问题求解方法,与经典粒子群优化算法相对比验证所提算法的有效性。Lakhdar B 等[3]针对机器人装配线中最小化能源消耗问题,提出了一种基于记忆的布谷鸟搜索算法(MBCSA),得出较好的装配线方案。Marcel A[4]提出了一种基于整数规划的优化方法来解决自动化装配线的动态资源重构问题,实现可重构生产,降低自动化装配线的生产成本,同时提高可持续性。Bao Z K 等[5]针对某型飞机总装线的平衡问题,提出了一种基于构造和改进的两阶段启发式方法,并建立了一个整数线性规划模型,有效降低了平衡工作站周期时间并最小化总资源投资成本。Niroomand S 等[6]通过人工电场算法以及模拟退火算法结合完整的编码方案,解决了直线型装配线平衡问题。Li Z 等[7]针对以成本为导向的装配线平衡问题,提出了一种多目标混合整数规划模型,并与多目标候鸟优化算法相结合,旨在缩短机器人采购周期和降低采购成本。Zhang B 等[8]针对混合模型U 型机器人装配线的平衡与排序问题,建立该双目标问题的数学模型,并对基本蜻蜓算法进行改进,最后与HMODA 算法进行对比体现出所提算法的优越性。Zhong Y[9]提出了一种有效的离散人工鱼群算法来解决以成本为导向的装配线平衡问题,该算法的目标是使建造成本最小化,通过大量的计算实验,验证了所提出的人工鱼群算法的有效性。郑谐等[10]针对飞机脉动式装配线平衡问题,建立飞机脉动式装配线站位内平衡问题模型,并结合改进的遗传算法,实现了脉动式装配线站位内的装配线平衡。
基于以上分析,装配生产线平衡问题的解决方法在不断发展和完善。不同的方法具有不同的特点,并且适用于不同的装配生产线平衡目标。由此,在研究装配生产线平衡问题时,需要综合考虑企业的生产状况、装配流程特点,并利用智能优化算法解决问题。
船用柴油机是典型的复杂产品,在传统固定式装配转型为脉动式装配线的过程中,其结构复杂、零部件繁多、装配工艺复杂等特点往往会导致装配作业分配不均衡、装配周期长、资源利用率较低等问题。基于以上分析,构建站位内装配生产线平衡的数学模型,制定装配作业分配规则,并通过混合优化算法对平衡方案进行求解。
1 脉动式装配线站位内平衡问题数学模型构建
本文主要研究船用柴油机脉动式装配线各站位内装配作业平衡分配问题,主要表现为:在满足工艺优先关系、站位内所有装配作业的完成时间不超过装配生产线节拍等约束条件下,将站位内的装配作业均衡、有序地分配给各个班组,并综合考虑了装配生产线的平衡率和平滑系数,以及本研究的目标是将站位内的装配作业分配实现均衡,并以最大化班组效率为优化目标。考虑船用柴油机脉动式装配流程,构建目标函数和约束条件。
(1)平滑系数(SI)
本文采用站位内所有班组空闲时间的标准差表示平滑系数。
式中:CT为装配生产线节拍;m为站位内班组数量;TTk(k=1,2,···,m)为班组内装配作业总时间。
(2)平衡率η
平衡率反映了产品的装配效率。本文采用装配线节拍与完成站位内所有装配作业的实际时间的比值表示平衡率。
式中:Tk为第k(k=1,2,···,m)个班组的实际装配时间。
为了优化船用柴油机脉动式装配生产线站位内的装配作业分配,选取平滑系数和平衡率作为优化目标,构建目标函数 minF(m)为
约束条件构建如下:
式中:Qk1和 Qk2分别为班组k1 和班组k2 的装配作业集合,k=k1、k2,且k1≠k2;H为站位内可用人员数量;xik表示第i项装配作业被分配到班组k中;Pij为第i项装配作业和第j项装配作业工艺优先关系,i,j=1,2,···,n,且i≠j。
上述公式描述了装配生产线站位内的优化条件,式(4)代表着每个班组不会重复进行相同的操作;根据式(5),每个班组必须遵守装配生产线规定的装配过程时间,以确保其准确性;根据式(6),为了确保每个班组能够顺利完成装配任务,所需的人员数量必须达到规定的标准,以支持并行装配,并且人员数量不会少于班组数;根据式(7)和式(8),每一个装配任务必须仅由一个班组完成并且保证所有装配任务完全分配;根据式(9),装配任务的安排应当遵循工艺优先原则。
2 构建基于遗传算法和蚁群优化算法(GAACO)的混合优化模型
2.1 设计算法流程
本文采用GA-ACO 作为一种混合优化算法,用于解决船用柴油机脉动式装配生产线的平衡问题。算法流程如图1 所示。
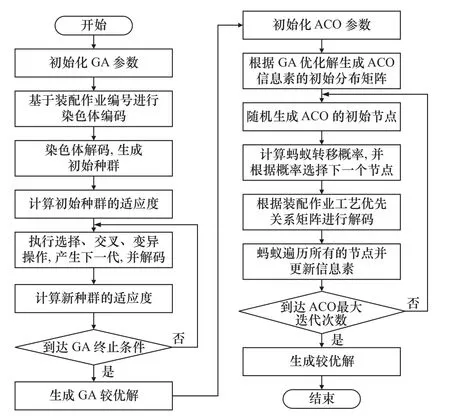
图1 混合优化算法流程
2.2 基于GA-ACO 的求解模型
为了解决脉动式装配线站位内装配作业平衡分配问题,将GA-ACO 与脉动式装配线站位内平衡问题数学模型相结合,以快速生成装配作业平衡分配方案,解决装配线平衡问题。
(1)遗传算法种群初始化
基于装配作业编号进行染色体编码,以避免运算量大的进制转换问题,同时随机生成初始种群用于GA 算法。此外,生成初始种群时需要考虑实际装配作业的工艺优先关系。
装配作业工艺优先关系有向图,如图2 所示。圈中和圈外的数字分别表示站位内装配作业编号以及对应站位内装配作业的工时(h)。
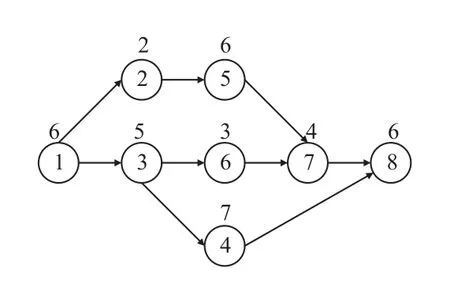
图2 装配作业工艺优先关系有向图
由图2 可知,根据设计的编码方式,生成了染色体序列[3,1,5,2,4,8,6,7]。然而,该序列并不符合装配作业的工艺优先关系。基于以上分析,根据装配作业工艺优先关系矩阵进行解码和调整,得到可行的染色体序列[1,3,2,5,4,6,7,8],具体流程如图3所示。
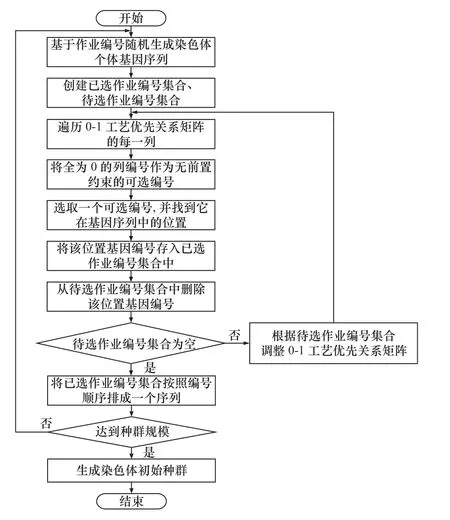
图3 种群初始化流程
(2)制定装配作业的分配规则
制定装配作业分配规则,将可行染色体个体代表的装配作业流程合理地分配到可选班组中,以解决装配生产线平衡问题,规则如下。
规则一:根据站位内所有装配作业累积工时与装配生产线节拍的比值,设置初始班组数量。如果比值包含小数部分,将比值向上取整。
规则二:当前待分配作业应分配到累计作业时间最少的班组中。
规则三:所有作业分配完毕后,若存在班组实际完成时间超过了CT,则重新调整班组数量。
具体流程如图4 所示。
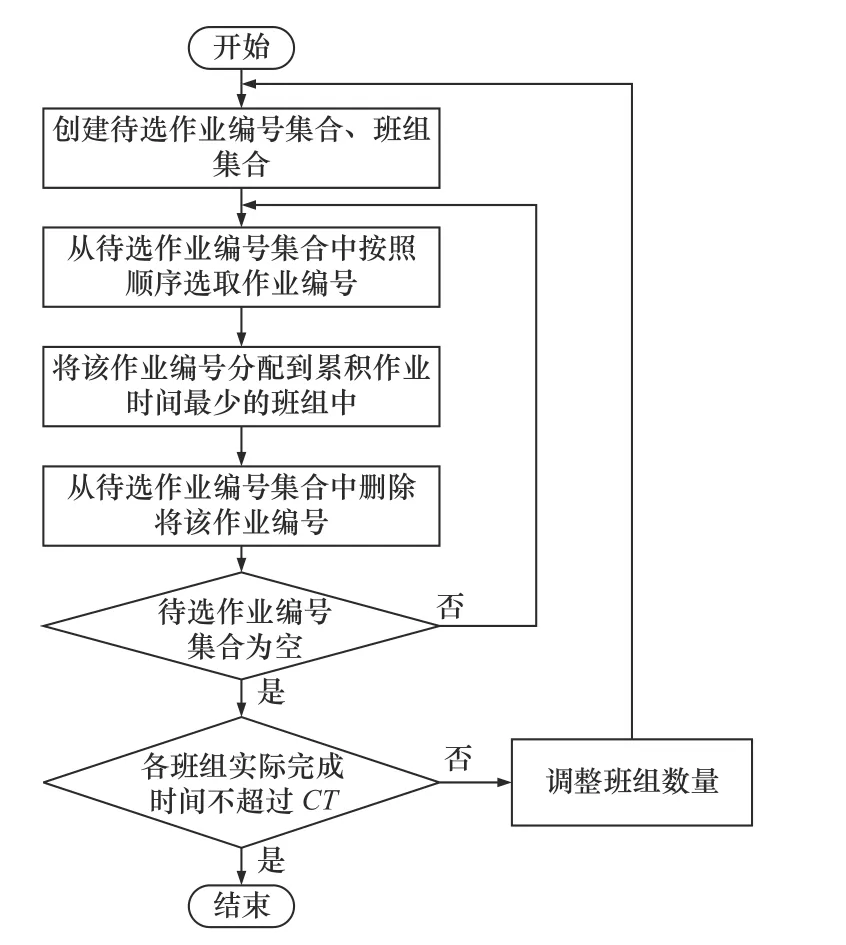
图4 站位内装配作业均衡分配流程
(3)染色体交叉、变异操作
设定交叉率PC,使用双点交叉方式生成新的染色体个体,以更大程度地改变其结构。通过在染色体个体上交换基因位置,以设定的变异率PM 来生成新的个体。
(4)计算蚁群转移概率以及构造路径
通过使用GA 和ACO 算法,创建一个高效的信息素初始分布矩阵,从而帮助蚂蚁找到最优的行进路线。为了更好地实现这一目标,将采用以下步骤。
步骤一:使用遗传算法(GA)得到的优秀解,基于信息素增强因子Q,更新蚁群算法(ACO)的初始信息素矩阵Tau(n阶矩阵)。在信息素矩阵Tau中,需要更新的位置被标记为Tau(bestChrom(i),bestChrom(i+1)),则:
式中:bestChrom(i)、bestChrom(i+1)表示遗传算法求得的较优装配作业排序中的相邻项,其中前者表示第i项作业编号,后者表示第i+1 项作业编号。
步骤二:从装配作业数范围内随机选择蚂蚁的初始节点,以初始化距离信息矩阵dimat。
步骤三:使用信息素矩阵Tau和启发值矩阵Eta,并基于信息素因子Alpha以及启发值因子Beta,构建了蚂蚁转移概率模型p,则有:
式中:currentNode表示当前选中的节点;temporarynextNode表示下一个待选节点;TAU(currentNode,temporarynextNode)表示需要更新信息素矩阵Tau的位置;ETA(currentNode,temporarynextNode)表示需要更新启发值矩阵Eta的位置。
步骤四:在获取节点之后,为其分配转移概率,并计算节点的累积转移概率。
步骤五:将随机数[0,1]与累积概率进行比较,选择下一个节点,更新蚂蚁的搜索路径。
步骤六:随着不断地迭代更新,若节点全部选取完毕,则执行步骤七,否则继续执行步骤五。
步骤七:鉴于蚂蚁路径与装配工艺的优先级不一致,为了使它们达到预期的效果,必须对它们进行解码处理,以此来满足装配工艺的优先关系需求。
步骤八:根据装配生产线的节拍CT约束,将已规划的路径中的装配作业均衡地分配到各班组中。
(5)全局信息素更新
蚂蚁每周遍历所有的装配作业号,生成装配作业序列,并更新最优解的信息素,吸引后者跟随。本文旨在提高算法搜索效率,采用全局信息素更新策略,选择最优蚂蚁对其进行全局信息素更新,并且只将信息素添加到当前的全局最优解中。更新公式:
式中:cost(u) 表示第u个蚂蚁的价值评价函数值;kv表示价值区间的下限;l表示价值区间范围大小;value(u) 表示第u个蚂蚁适应能力值;mincost表 示种群适应度下限;maxcost表示种群适应度上限;route(r) 表示第u个蚂蚁路径中第r个节点;Tau(route(r),route(r+1))代表信息素矩阵Tau中需要更新的位置;rho为信息素挥发系数,取值范围为[0,1]。具体步骤如下。
步骤一:记录 maxcost和 mincost。
步骤二:使用适应度上限 maxcost和适应度下限mincost对价值区间进行归一化,并创建蚂蚁个体的价值评估函数cost(u)。
步骤三:利用增强因子Q、挥发系数rho和价值评价函数cost(u),更新信息素矩阵Tau。
3 实例验证
基于上述数学模型和约束条件,使用GA-ACO混合优化算法进行船用柴油机脉动式装配生产线预装站位内所有装配作业的均衡分配的验证。
表1 详细列出了预装站位内的装配作业,而图5展示了这些装配作业之间的工艺优先关系。根据表1 和图5,将预装站位内的装配作业转化为工艺优先关系矩阵图,如图2 所示。

表1 预装配站位内的装配任务
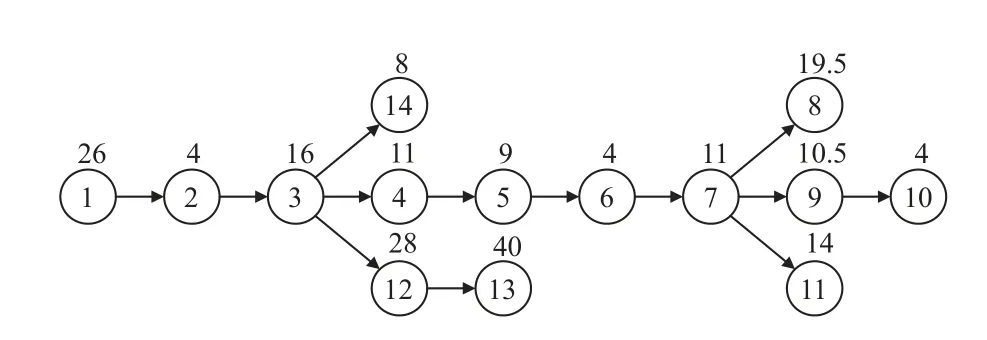
图5 预装站位内装配作业工艺优先关系有向图
假设在给定条件下(预装站位的工期为12 天,每日工时为10 h,可用工人数量为6 人),进行优化方案的计算。这些方案旨在实现装配作业的均衡分配。尽管这些方案可能会在装配作业的顺序安排上存在差异,特别是在非关键路径上的装配作业的分配方式可能有多种选择,但它们都满足了相同的目标和约束条件。图6 所示为一种较优的装配作业均衡分配方案的甘特图,班组分配结果见表2。将算法分配结果与现场人工分配结果进行比较,比较结果见表3。现场人工分配根据装配作业的工艺优先关系和人工经验,确保预装站位内的装配作业完成时间不超过生产节拍(图7)。

表2 预装站位内班组分配结果
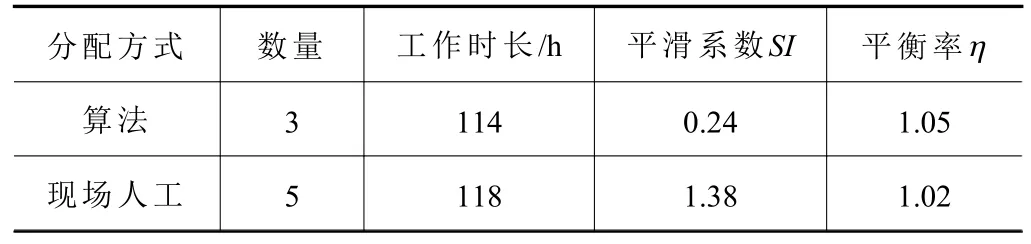
表3 预装站位内装配作业分配方案对比
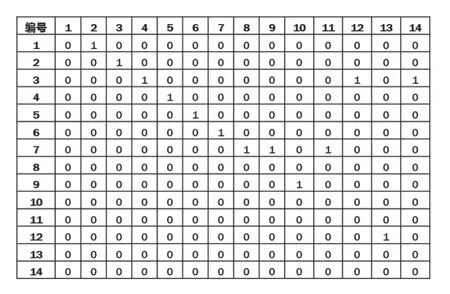
图6 预装站位内装配作业工艺优先关系矩阵图
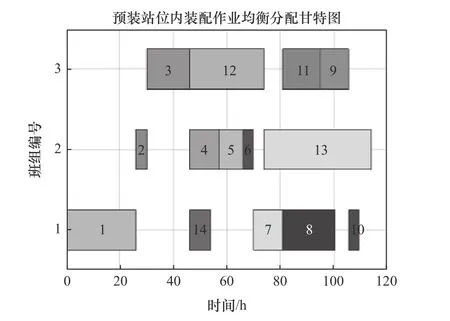
图7 预装站位内装配作业均衡分配甘特图
由图8 可知,本文所提的 GA-ACO 混合优化算法在处理装配作业繁多的装配线平衡问题上,相比单一的 GA 能够更有效且较快地求解出装配线平衡问题的最优解。
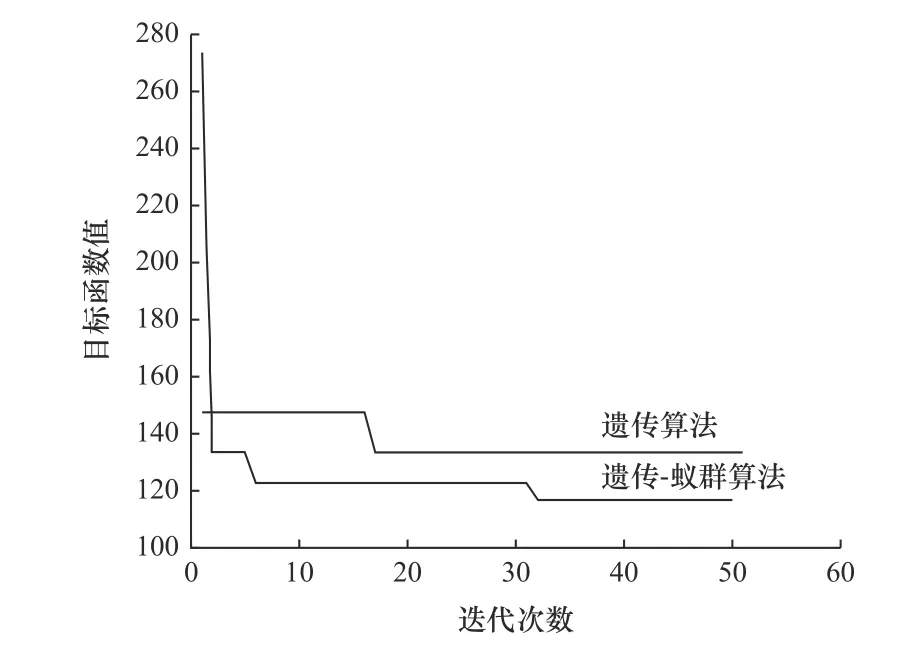
图8 GA、GA-ACO 混合优化算法迭代优化对比图
由表3 数据可见,采用算法分配方式可以节约班组数量2 个,缩短工期4 h,降低了1.14 的平滑系数,提高了3%的平衡率。
基于以上分析可知,通过算法分配方案,可以实现班组数量减少、工期缩短和装配作业更均衡地分配的优势。
4 结语
本文聚焦于解决船用柴油机脉动式装配生产线平衡问题,提出一种基于混合优化算法的脉动生产线站位内装配作业平衡分配方法。
(1)本文致力于解决装配生产线的平衡问题,通过考虑节拍、班组数量和装配作业间的工艺优先关系等约束条件,建立了一个数学模型,并提出了一套装配作业分配规则,以提高班组效率和实现装配作业的均衡分配。
(2)结合数学模型及装配作业分配规则构建了GA-ACO 混合优化算法模型,并以某船用柴油机预装站位内所有装配作业为验证对象,证明了该方法的有效性。
