基于半解析法的面铣削力系数快速标定与验证*
2023-12-11陈荣荣
张 媛 陈荣荣
(西安交通工程学院机械与电气工程学院,陕西 西安 710300)
铣削加工是常见的减材制造方式之一[1],铣削加工具有加工效率高、应用范围广和加工精度好的特性[2-4],广泛应用于航空航天[5]、汽车模具[6]和石油机械[7]等领域。铣削力是铣削过程中重要的输出参数,也是表面完整性、残余应力和刀具磨损的重要影响因素[8-11]。同时,铣削力是选择切削参数的依据,也是优化切削参数的关键。因此,有大量学者从事铣削力的预测研究[12-13]。
铣削力与切削参数、刀具几何角度[14]和工件机械特性密切相关,其映射关系直接体现了铣削力的预测精度和效率。大量学者研究了铣削力的建模方法,用于构建铣削力解析模型[15-17]。Lee P 等利用材料的塑性变形理论,基于屈雷斯卡屈服准则,建立了铣削力解析模型[18],该模型是基于基本的二维直角切削得到。Wang J 等进一步发展了文献[18]的铣削力模型,构建了切削过程中材料的流动速度关系图,给出了基于最小能量原理的剪切角计算方法[19]。高腾等基于赫兹接触理论,建立了复合材料单纤维切削力模型[20]。Baker M 指出尽管上述模型[16-19]反映了铣削过程的刀具几何参数和工件的物理属性[21],但铣削力系数的计算十分复杂,需要求解切屑流动角、法向摩擦角和法向剪切角,且该类解析模型依赖铣削加工实验,否则无法得到相关参数值。因此,一些研究者尝试使用其他方法预测铣削力。
随着计算机技术的快速发展,有限元法求解铣削力引起一些学者的关注。有限元法是基于工件材料的边界条件和本构方程,通过将工件离散为若干个微元,根据微元节点之间的相互关系和材料的塑性行为,构建大型稀疏矩阵。基于矩阵的大规模运算,进而得到铣削力。近些年,随着计算能力的快速提升,有限元法在铣削力预测中的应用日渐广泛[22-23]。有限元方法根据是否需要判定切屑分离分为欧拉法(Eulerian)[24]和拉格朗日法(Lagrangian)[25]。欧拉法不需要判定切屑分离,但是需要预判切屑的形状,这两种方法分别适用于不同的场合。Kim K W分析了加工中的流动应力,采用有限元探讨切削力系数中摩擦因子的变化规律[26]。张耀满等建立了球头铣刀切削Ti-6Al-4V 的有限元仿真模型,研究了铣削力在时域的变化[27]。Gao H 进一步提出了拉格朗日-欧拉组合法,结合了拉格朗日法和欧拉法的各自特点[28]。然而,有限元仿真模拟在二维切削加工中效率尚可,三维加工的模拟效率较低,但现实中的铣削加工均为三维加工。因此,对于复杂刀具和工件的加工,有限元法存在一定的不足。
Engin S 等提出了平均铣削力系数的概念[29]。一些学者采用数据处理的办法,将铣削力表示为系数的指数函数。王刚等使用改进的粒子群模糊系统获取指数铣削力模型的未知参数,并采用钛合金进行铣削加工实验,结果表明预测的切削力和实验值误差较小[30]。丁悦等将铣削力系数表示为切削参数的多项式函数[31]。王海艳等基于全因子实验,研究了复合材料螺旋铣削瞬时切削力系数的识别方法[32]。刘显波等提出了多目标优化算法求解铣削力系数[33]。上述方法均基于铣削加工实验,采集大量的数据并使用算法处理。智能优化算法求解复杂,需要迭代更新。本文提出面铣削力系数的半解析法,基于矩阵运算直接求解铣削力系数。
1 刀齿微元的铣削力建模
铣削包括平面铣、铣槽和仿形铣削,平面铣削加工十分常见,面铣削是其他复杂铣削加工的基础;多轴复杂铣削加工的基本力学机理是面铣削的扩展和延伸。因此,研究面铣削是深入研究其他铣削加工的前提,平面铣削过程如图1 所示。
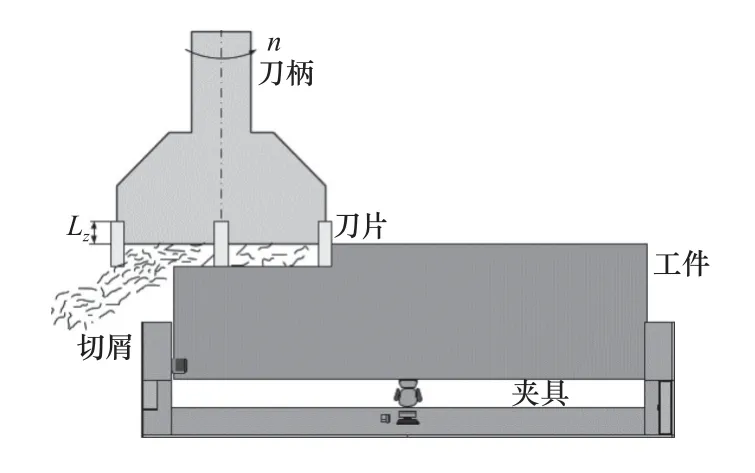
图1 平面铣削示意图
铣削加工是一个断续切削过程,图1 中刀具有四个刀齿,刀具旋转一周,刀齿按时间序列依次切入工件。刀具沿着自身轴线做旋转运动,同时沿着进给方向移动,铣刀刀齿的运动包括旋转运动和进给运动,刀尖点的运动轨迹为周期性的摆线运动。逆铣削通常用于精加工。图1 中用垂直于刀具轴线的平面截切刀具和工件,得到沿着刀具轴向的微元,微元受到的铣削力如图2 所示。在刀具的旋转中心建立刀具坐标系x-y-z,坐标系的原点o位于刀具底端面的旋转中心,x轴垂直于工件表面并指向工件内部,y轴与刀具进给方向相同,z轴正方向是x轴和y轴的矢量积方向。任意瞬时刀齿所在的位置与x轴的夹角定义为啮合角θ,微元受到的铣削力为切向力(θ)、径向力(θ) 和轴向力(θ)。
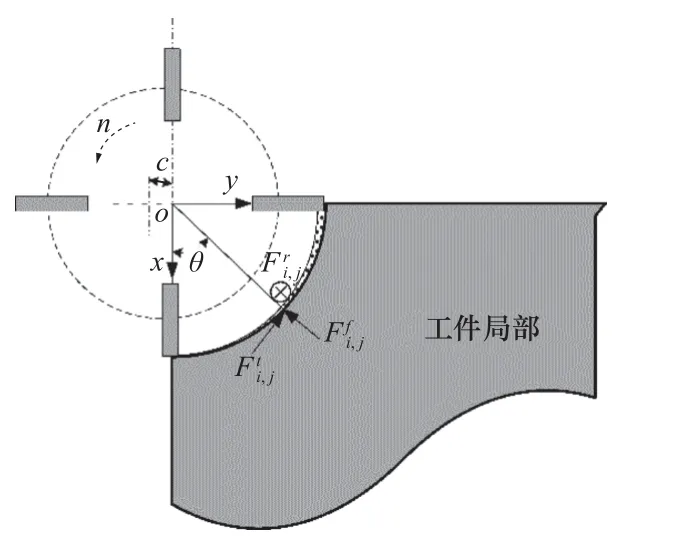
图2 刀具受力示意图
从图2 可知,刀齿刚开始切入工件的未变形切屑厚度为零,随着刀具的旋转和进给,未变形切屑厚度逐渐增加。任意瞬时刀齿的啮合角为θ,刀齿j的第i个微元受力可以表示为[29]
式中:θ为啮合角,(°);Ktc为切向力系数,N/mm2;Kfc为径向力系数,N/mm2;Krc为轴向力系数,N/mm2;bi,j为微元的轴向宽度,mm;hi,j为微元的瞬时未变形切屑厚度,mm;Kte为切向刃口力系数,N/mm;Kfe为径向刃口力系数,N/mm;Kre为轴向刃口力系数,N/mm。
已有的研究表明[34],在铣削加工中刃口力系数很小,故刃口力很小。因此,对于一般的常规铣削加工,刀具的刃口力可以忽略不计,则式(1)可以简化为
式中的瞬时未变形切屑厚度hi,j(θ)可以表示为
式中:c为每齿进给量,mm/f。
根据铣削加工时机床设定的进给速度,可以计算得到每齿进给量c。刀齿微元的接触宽度根据式(4)得到:
式中:Lz为刀具的轴向切深,mm;n为微元数,刀具微元划分得越精细,n的取值越大。
在铣削加工中,现有的实验设备只能测量沿着机床主轴方向的切削力,故将微元力投影到刀具坐标系x-y-z下,则投影后的力为
铣刀的齿间角 θa是相邻两个刀齿切入工件的相位差,齿间角与刀齿数相关,其表达式为
沿着刀具的轴线方向,各个方向微元的总铣削力为
由式(7)可知,总铣削力是全部微元力的叠加。其中,切向力直接影响机床所需的功率。刀具受到的总铣削力合力为
2 铣削力系数的快速标定
2.1 铣削力系数的标定方法
传统的铣削力系数计算需要求解剪切角、摩擦角和切屑流动角,由于多个参数相互耦合,剪切角的计算十分困难。本节提出基于矩阵运算的切削力系数快速标定方法,根据机床-刀具-工件的特性可知,铣削力是设置切削参数的约束条件。由式(2)可得,铣削力的预测需要首先求解铣削力系数Ktc、Kfc和Krc。根据式(5)可以推导出:
则第j个刀齿受到的铣削力可以表示为
对式(10)进一步化简,整理为几何参数与系数矩阵的形式:
式(11)的第一个矩阵反应了铣削中几何参数对切削力的影响,主要由切削深度和每齿进给量共同影响;第二项为铣削力系数,主要由工件的物理特性、屈服极限以及刀具的几何特性影响,式(11)简记为
铣刀所处的位置不断变化,其啮合角也随之改变,任意瞬时对应的铣削力为
式(13)简记为
基于矩阵的计算规则,铣削力系数矩阵K可表示为
式中:右端力矩阵F可由测力仪测量得到,矩阵A由刀具几何角度和切削参数计算得到。通过铣削实验,可以求解得到铣削力系数。
2.2 峰值铣削力系数的修正
铣削加工是断续切削,切削力随着时间周期性变化。随着切削力从零开始逐渐增大,刀具和工件的振动更加剧烈,在切削力的峰值处,刀具和工件的振动最为剧烈,振动将进一步导致切削力发生变化。切削力峰值对刀具寿命、加工误差和变形程度影响极大。由于振动和切削力相互耦合在一起,理论上很难直接分离振动引起的切削力。因此,引入修正因子对式(15)进行修正,使得预测的切削力峰值和真实值更接近。式(15)引入修正因子ξq(q=t,f,r),则有
函数 ξq(q=t,f,r)只对切削力峰值进行修正,在刀齿的其他切削阶段为常数1,则系数 η为
3 实验标定系数及铣削力验证
铣削力实验使用的测力仪为Kislter 9367C,数据采样为三通道,X轴和Y轴方向的灵敏度为-7.6 pc/N,X和Y方向的量程为0~10 kN;Z轴方向的灵敏度为-3.9 pc/N,Z方向的量程为0~60 kN。实验使用的信号放大器为Kislter8050A,放大器零飘低于0.15 mA,实验过程的采样频率为10 kHz。数据采集器为DEWESOFT X3,通道数为8,数据实时显示的计算机为DELL G15 5520。机床为三轴立式铣床,刀柄为机械锁紧刀柄,铣削时不使用冷却液。刀具几何参数见表1,使用两种规格的刀具进行铣削加工实验。为了保证刀具的安装精度,加工前将刀具安装到刀柄,在机外用瑞士Evoset AG 公司生产的TOOL MASTER 对刀仪对刀具进行校准,以减小刀具的安装误差和偏心。
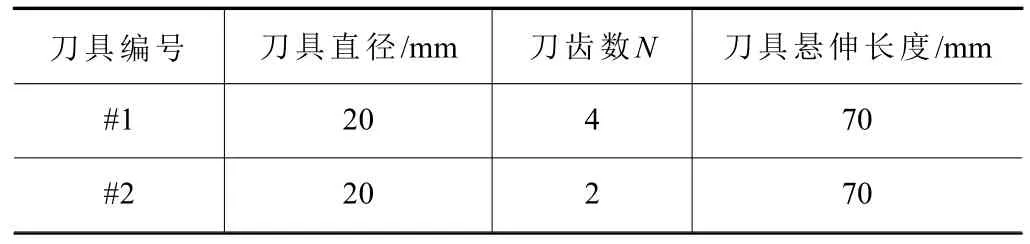
表1 刀具几何参数
工件材料为航空Al 7075,工件尺寸为100 mm×100 mm×50 mm,工件材料的物理特性见表2。铣削方式为逆铣削加工,逆铣加工中刀具受到工件的作用力远离工件的已加工表面,故精加工中常采用逆铣加工。

表2 工件材料的物理特性
铣削力的测量设备连接如图3 所示。在铣削过程中,工具受力传递到测力仪,测力仪通过压电效应传递信号。刀具受到的力经过放大器和数据采集器最终传输到计算机,经过计算机处理得到实时铣削力。为了保证实验的准确性,工件安装完毕后,用刀具首先去除材料表面的余量,对工件表面进行精加工预处理。切削时要保证刀具轴向深度均匀一致,以消除工件安装误差,同时防止工件表面存在的氧化皮导致预测不准。
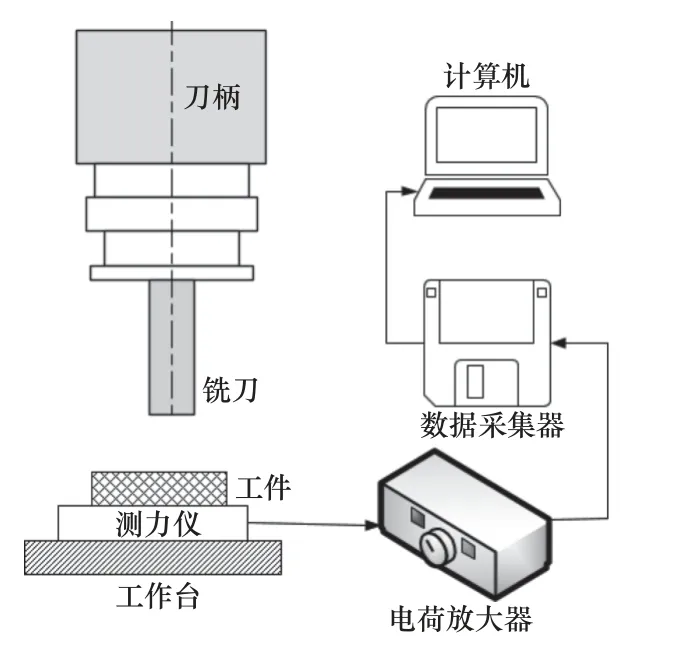
图3 实验设备连接图
切削过程中使用的铣削参数及铣削方式见表3,第1~2 组为实验标定铣削力系数,第3~4 组为对标定的铣削力系数进行检验。
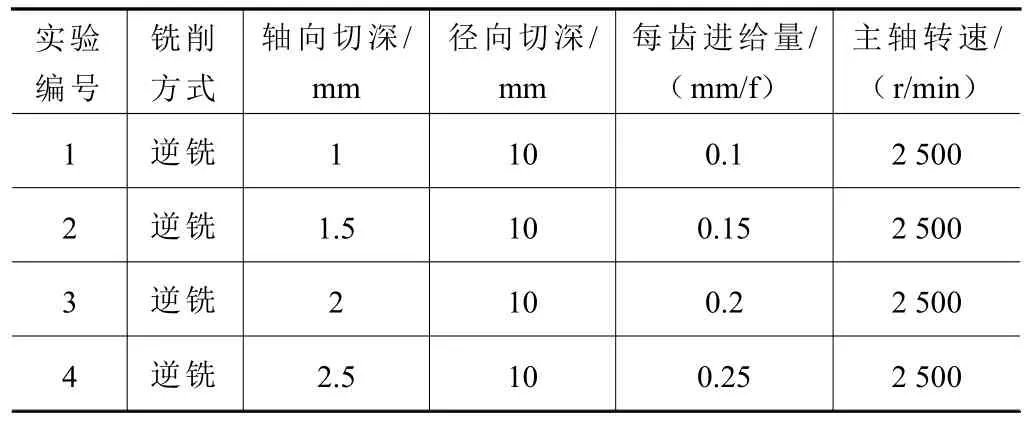
表3 切削参数
通过改变每齿进给量和轴向切深,用测力仪分别测量实时铣削力。刀具#1 铣削力随旋转角度的变化如图4 所示。铣削是周期性的力,刀具铣削力在一个周期内交替变化,其余时间均是第一个周期的延续,故图4 只给出了一个完整周期内铣削力的变化。
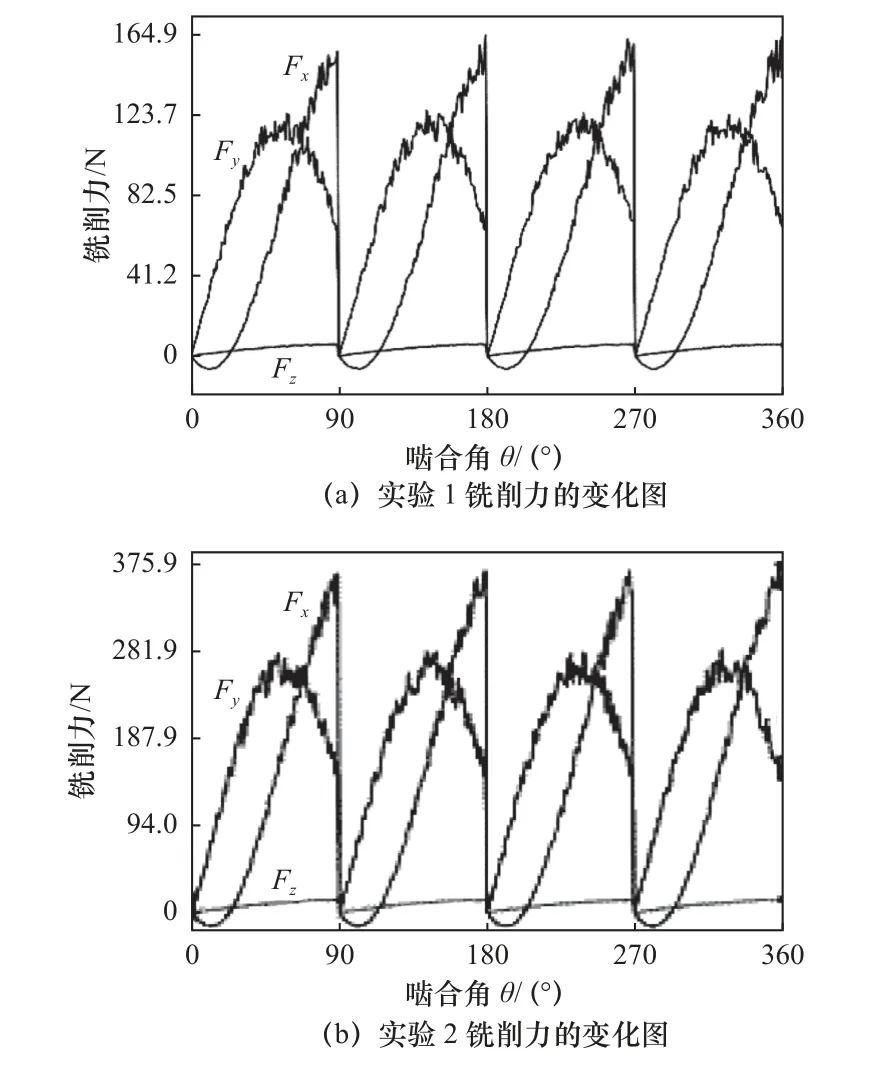
图4 刀具#1 铣削力变化图
实验测量的刀具#2 铣削力的变化如图5 所示,图5 中铣削力出现明显的断续,主要是刀具结构引起的。刀具#2 只有两个刀齿,一个周期中只有一半的时间处于工作状态。两个刀齿相位差为180°,故啮合角在90°~180°没有铣削力。由图4 和图5可知:啮合角从0°开始逐渐增大,铣削力随之增加,达到峰值后逐渐减小;铣削力Fx最大,Fz最小,在平面铣削过程中力Fx为主切削力。
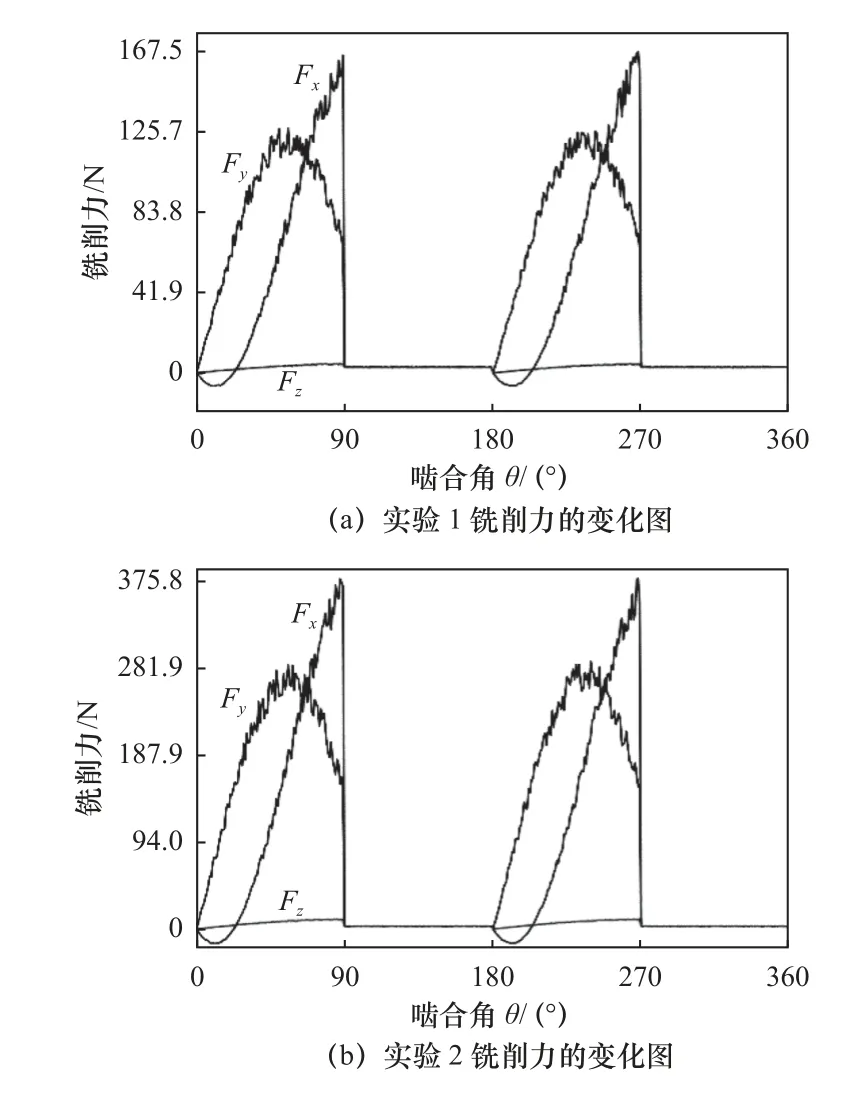
图5 刀具#2 铣削力变化图
刀具#1 铣削合力随啮合角的变化如图6 所示。通过图6a 和图6b 对比可知:铣削合力的图形变化趋势一致,图6b 的铣削力峰值明显高于图6a,表明随着铣削深度和每齿进给量的增加,铣削合力增大。因此,铣削力与切削深度和每齿进给量呈正相关。
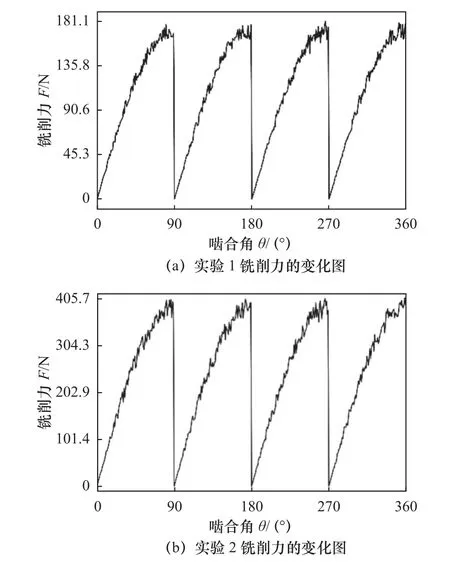
图6 刀具#1 总铣削力变化图
图7 所示为刀具2 铣削力合力随啮合角的变化图,可以看出在刀具旋转的一个周期内,啮合角为0°~90°和180°~270°范围内存在铣削力;图7b的铣削力峰值高于图7a,这是轴向切深和进给量增大引起的,单位时间切除的材料体积增加。因此,切削参数增大引起铣削力升高。
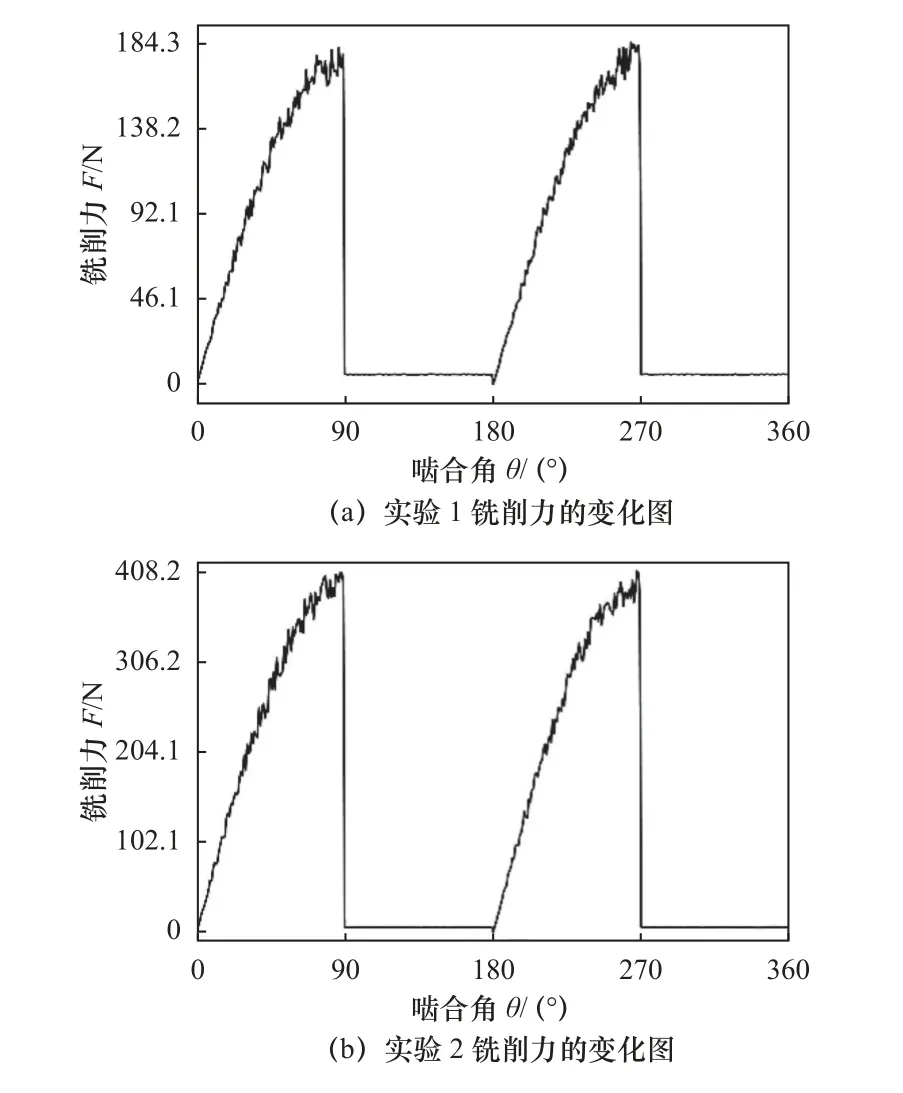
图7 刀具#2 总铣削力变化图
根据式(15),基于测量的铣削力可以推导出刀具#1 和刀具#2 的铣削力系数,见表4。从表4 铣削力系数可知,切向力系数最大,铣削加工轴向力较小。刀具#1 的铣削力系数与刀具#2 的铣削力系数不同,这是刀具的其他几何参数不同导致的。
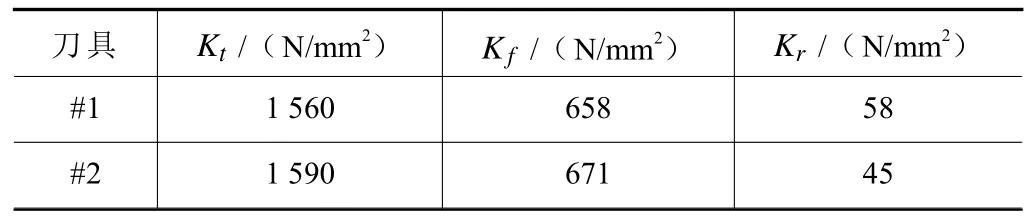
表4 铣削力系数
使用基于表4 得到的铣削力系数预测铣削力。使用不同的每齿进给量和铣削深度进行实验检验,见表3 中的3~4 组参数,分别进行铣削加工实验。刀具#1 铣削力预测值和实验值的对比如图8 所示,刀具#2 铣削力预测值和实验值的对比如图9 所示。通过实验值和预测值,可以得到实验3 切削力系数的修正因子ξq(q=t,f,r)分别为1.14、1.08 和1.05;实验4 切削力系数的修正因子 ξq(q=t,f,r)分别为1.17、1.09 和1.06。
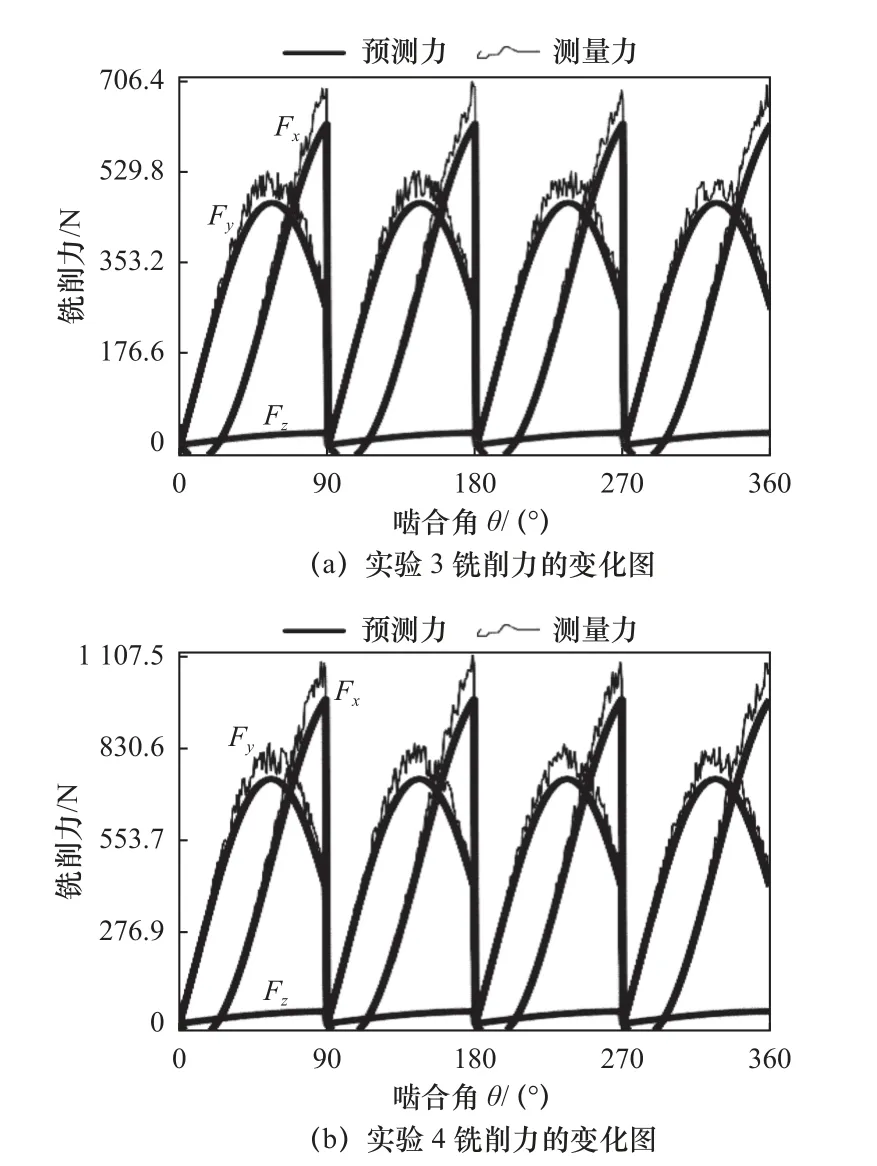
图8 刀具#1 铣削力预测值和实验值对比
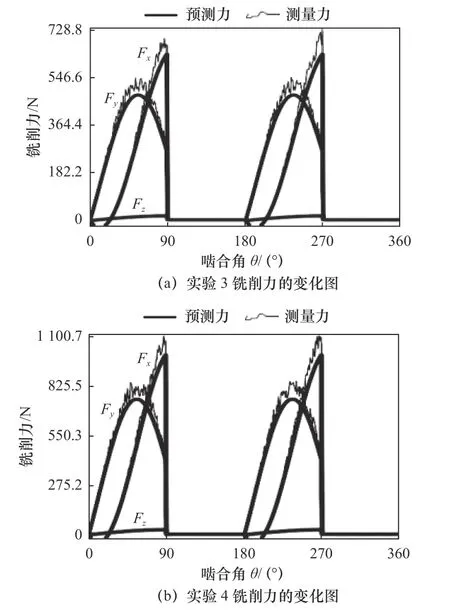
图9 刀具#2 铣削力预测值和实验值对比
刀具#1 铣削力合力预测值和实验值的对比如图10 所示。由图10 可知,铣削力合力的预测值和实验值接近。铣削合力在啮合角为90°、180°、270°时非连续变化,从最大值直接变为0。以啮合角90°为例,刀具啮合角在接近90°时,铣削力逐渐增加到最大值;达到90°时当前工作的刀齿离开工件进入非切削区,下一个邻近的刀齿进入切削区开始切削工件,故铣削力出现突然变化。
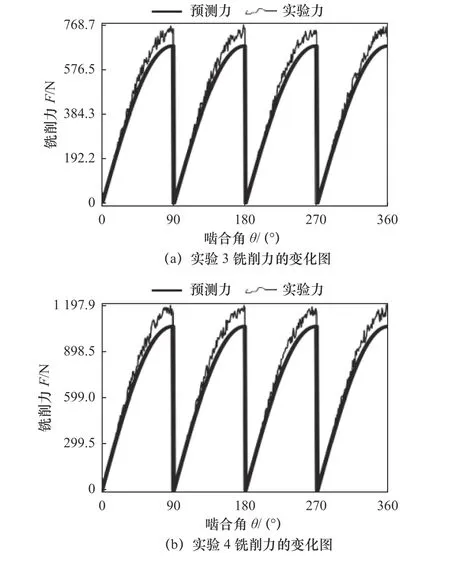
图10 刀具#1 总铣削力预测值和实验值
图11 所示为刀具#2 铣削力合力预测值和实验值的对比图。刀具#2 只有两个刀齿,故在一个周期中啮合角在90°~180°和270°~360°铣削力为零,即不存在铣削力,刀具处于非切削状态。图11b 铣削力峰值比图11a 铣削力峰值大,这主要是铣削参数增大,刀具啮合的材料增多导致的。
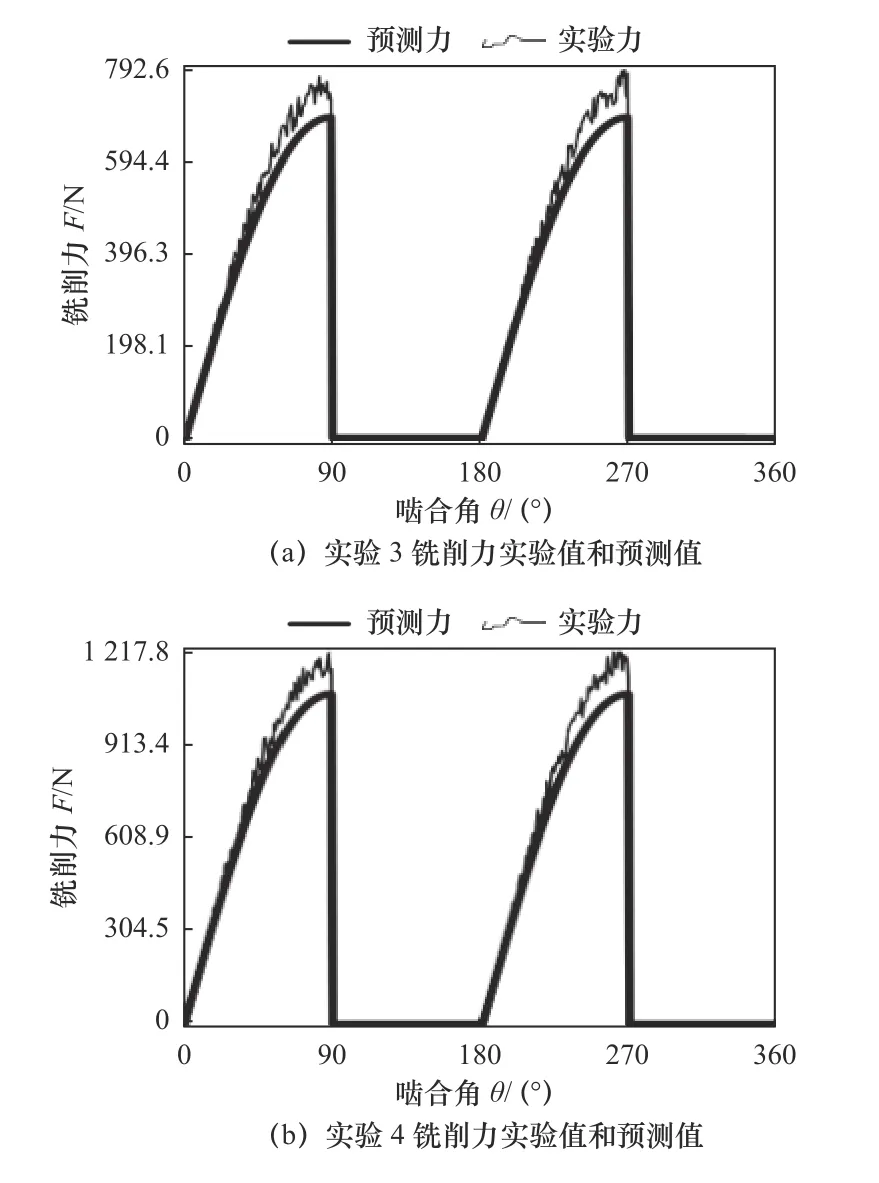
图11 刀具#2 总铣削力预测值和实验值
由图8~11 可知:铣削力的预测值和实验值接近。各次实验测量的铣削力和预测值的最大相对误差见表5,刀具#1 铣削力Fx、Fy和Fz预测值和实验值最大相对误差分别为10.1%、11.4%和9.2%;刀具#2 铣削力Fx、Fy和Fz预测值和实验值最大相对误差分别为9.5%、8.7%和9.4%。因此,本文提出的直齿面铣削加工的铣削力系数快速标定方法精度较高。

表5 铣削力预测值和实验值的误差
4 结语
本文建立了铣削力系数的快速标定方法,通过分析刀具轴向微元的受力,得到总铣削力的表达式。基于实验数据得到铣削力系数,并进行实验验证。基于标定的铣削力系数,设定不同的切削参数进行铣削力的预测,并对铣削力峰值力系数进行了修正。一系列的铣削实验表明:铣削力的预测值和实验值接近,相对误差小。本文研究可以得到以下主要结论:
(1)基于本文的铣削力标定方法,预测的铣削力Fx、Fy和Fz最大误差分别为10.1%、11.4%和9.4%。因此,本文提出的标定方法具有较高的预测精度和可信度。
(2)切向力系数Kt最大,径向力系数Kr最小,切向力系数Kt是进给力系数Kf的2.37 倍。因此,面铣削中的主要切削力来自切向力,铣削加工中应控制切向力的峰值,以便减小刀具磨损和零件变形。
(3)切削深度从1 mm 增加到2.5 mm,每齿进给量从0.1 mm/f 增加到0.25 mm/f,铣削合力F增加6.64 倍。随着切削参数的增大,铣削力增加。因此,铣削力与切削参数正相关。
