基于五次B样条插值在机械手轨迹规划中的研究

2023-12-09郭北涛涂修贤姜旭

机械工程师 2023年11期

郭北涛，涂修贤，姜旭

（沈阳化工大学机械与动力工程学院，沈阳 110142）

0 引言

工业机器人作为由人工智能、电子信息、自动化技术等多门学科交叉融合所产生的智能现代化设备，其不仅可以提高产品质量精度，同时还可以极大地提高工作效率，已经在汽车、航空航天、工程机械、工业铸造等多个领域广泛应用[1]。无损检测技术是指在不损害或者不影响被检测对象性能的前提下，采用涡流、超声、射线等技术对被检测对象进行缺陷、物理、化学等参数检测分析，是工业发展不可或缺的关键技术[2]，已经在各个领域得到了广泛的应用。随着整个社会对产品质量和产品精度的要求越来越严格，提高无损检测的精度和工作效率实现自动化检测俨然已经成为一个发展的必然趋势，而机器人学的发展，正好为实现无损检测自动化提供了巨大的支持，因此将机器人学和无损检测结合实现无损检测自动化成为研究的热点。

在制造业快速发展的今天，各种曲面工件广泛地应用在各种现代化设备中。工件的制造精度直接影响从动件的运动精度[3]，所以为了达到满足工作需求的运动特征，必须要对工件表面进行缺陷检测以保证曲面工件的制造精度，本文提出的机械手与涡流检测装置结合的涡流自动检测系统就是在此情况下应用。但针对曲面工件进行检测时，探头需要与工件保持一个稳定的工作距离以获得稳定的数据，对工作的稳定提出了较高的要求。因此，高精度的轨迹规划研究是很有必要的。

在机械手的轨迹规划方面，袁旭华等[4]提出了改进B样条曲线和优化搜索策略蜂群算法相结合的规划方法；周远非等[5]提出了基于拉格朗日动力学对机械臂建模，并利用均匀5次B样条函数来构建运动轨迹；谢嘉等[6]通过构建5自由度机械臂数学模型，分析计算出其正逆运动算法。

研究中主要对凸轮工件的曲面表面进行五自由度串联机械手跟踪的轨迹规划，首先在任务空间中选取多个所要经过的检测路径点, 在已知多个检测路径点的前提下，通过机械手臂动态运动学的分析，应用逆向运动学对检测路径点的坐标进行求解，得出机械手臂各关节的转动角度，再通过正向运动学进行解正确性的验证，对验证后的关节转动角度进行曲线插值规划，在曲线插值规划之后生成各关节转动角度的检测轨迹函数，完成对机械手臂各个关节的轨迹规划[7]。

1 曲面工件涡流自动检测系统结构

曲面工件涡流自动检测系统由由机械手臂控制系统与涡流缺陷检测采集系统两大部分组成。第一部分为机械手臂控制系统，由上位机、五自由度串联机械手臂等构成。在检测过程中将被检测曲面工件凸轮工件的位姿坐标应用所编写的正向、逆向运动学程序，转化为机械手臂各个关节转动角度，通过五次B样条曲线进行轨迹规划，再应用所提出的算法对机械手臂跟踪的检测轨迹进行时间最优轨迹规划，将规划好的轨迹程序输入上位机中，通过上位机对机械手臂发出控制指令，使得机械手臂夹取涡流探头按照规划的轨迹对凸轮工件表面缺陷进行检测。

第二部分为涡流缺陷检测采集系统，由工控机、涡流采集卡、涡流检测仪器和探头等构成。随着机械手臂按照所规划的轨迹夹持探头对凸轮工件表面缺陷进行检测，涡流采集卡对凸轮工件表面缺陷信息进行实时采集，并将缺陷信息传输到工控机中，由工控机中的检测软件对缺陷信息进行处理，并显示凸轮工件表面缺陷信息，最终完成凸轮工件表面缺陷自动检测工作。

2 机械手轨迹规划分析

2.1 正向运动学求解

正向运动学是在得到机械臂每个杆件长度的情况下，对于机械手臂的每个关节角度的变化量，通过计算得到末端执行器在坐标下的相对位置和姿态。相邻的关节坐标系可用齐次矩阵i-1i T的样式来描述各自的姿态，所以每个关节坐标系本质上是在前一个关节坐标变换后进行下一次变换，所以将矩阵右乘就得到坐标系{Ai-1}向坐标系{Ai}的变换矩阵：

所以i-1i T的表达式如下：

通过上述分析可知，从基底到机械手末端执行器的变换矩阵形式为

则将上述矩阵依次相乘可得机械手臂末端执行器在空间坐标系中的准确位姿，矩阵表达式如下：

通过上述对机械手臂正向运动学的分析，在已知机械手各关节变量、连杆长度、连杆偏移等参数的情况下，可明确机械手臂末端执行器精准的位置和姿态。

2.2 逆向运动学分析

逆向运动学是在已知末端执行器的位置和姿态的基础上，求解出机械手臂各个关节的转动角度。由于逆向运动学的特殊性，往往存在多解甚至存在无解的情况。所以求解机械手臂逆向运动学方程，选取逆向运动学的解，成为分析好逆向运动学的关键，也是机械手臂轨迹规划的重要基础。

本研究结合所研究曲面工件涡流自动检测系统中机械手的结构特性，使用代数法与几何法相结合的方法来求解逆解。

1）几何法求解机械手关节角θ2、θ3、θ4。

将所研究的五自由度串联机械手进行平面投影，投影模型如图1所示。机械手臂的末端点P（x，y）的横纵坐标最终由3个部分组成（x2+x3+x4，y2+y3+y4）。图1中的θ2、θ3、θ4就是我们要求解的机械手舵机的变化角度，即运动学方程的逆解。α为末端执行器与水平面的夹角。

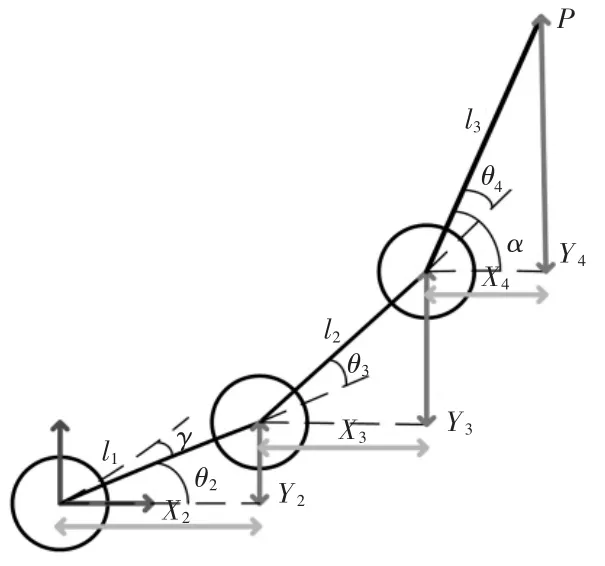
图1 机械手臂平面投影

求解θ3：

设

根据余弦定理，设

则

求解θ2，

当θ3＜0时，

或当θ3＞0时，

求解θ4：

2）代数法求解机械手关节角θ1、θ5。

根据式（12）第2行第4列中对应元素相等即可求得θ1：

根据式（12）中第2中第2列中对应元素相等可知：

至此通过几何法和代数法的分析，已全部求解出五自由度串联机械手臂各关节变化量的函数表达式，在应用机械手臂检测凸轮工件的曲面表面的缺陷实验过程中，通过给定某个末端执行器的姿态，使用上述函数表达式得到机械臂各关节的转动角度。

2.3 五次B样条轨迹规划

B样条曲线对于机械手臂轨迹规划具有较高的契合度，可对机械手进行实时动态控制[8]，能够达到所研究的机械手对凸轮工件表面缺陷进行涡流无损检测的控制要求。B样条函数是一个由节点矢量的非递减参数n的序列所决定的k分段多项式[9]，其曲线的函数表达式如下：

式中，u∈（uk-1，un+1），i=0，1，…n。

B样条曲线对机械手臂各关节角度转动值的轨迹规划是：首先根据逆运动学的分析，将机械手臂末端执行器所经过的检测路径点坐标转换为机械手臂各关节角度的转动值，再通过B样条曲线对各关节角度的变化量进行插值计算，从而求解出机械手臂各关节角位移与时间的关系。求解关于机械手臂各关节角位移的B样条曲线函数表达式，首先必须求解控制顶点Pi与节点向量U。

1）求解节点向量U。

现设关节角位移的时间序列为T（θi，ti），其中i=0，1，…，n，机械手从运动开始到运动结束所用的总时间为ttotal=tf-t0，同时利用累加弦长参数化，根据长度比例关系来对时间进行归一化。这种参数法反映了控制点按弦长的分布情况，可以解决控制点按弦长分布不均匀的情况下采用均匀参数化所出现的问题，其表达式如下：

2）求解控制顶点Pi。

根据在任一确定的区间［ui，ui+1］内，存在不超过k+1个非零基函数Bj，k，即Bi-k，k，…Bi，k的原则。因此在区间［ui，ui+1］上的机械手臂关节角位移θi的B样条曲线函数可改成：

将在节点区间［uk，un+k］内的节点值代入到式（17）中可得到n+1个方程表达式：

式中，ui+k∈［uk，un+k］，n=0，1，…，n。

因为求解n+k个控制点需要有n+k个约束条件，现有n+1个约束条件，故现在增添k-1个约束条件即设起点与终点速度为v0、vf，起点与终点的加速度为a0、af。则表达式如下：

通过式（19）～式（21）可解的方程：

其中五次B样条函数系数矩阵CB形式如下：

3 轨迹仿真分析

现以机械手臂第四关节为例，取10个第四关节所经过的路径点作为插值点，应用逆运动学编写的Matlab程序，将所选取的路径点坐标转化为机械手臂各关节角度转动值，如表1所示。

表1 机械手第四关节转动角度（°）

设置两路径点之间的时间间隔为2 s，编写的三次样条与五次B样条插值函数程序在Matlab中进行轨迹仿真，仿真结果如图2、图3所示。

图2 三次样条运动轨迹曲线

图3 五次B样条运动轨迹曲线

在通过以上几种方式对比分析，如图2所示，三次样条轨迹解决了加速度不连续的问题，但是其加速度曲线变化不平滑易于产生误差，影响检测精度，且其加加速度曲线不连续，容易对机械手臂产生较大的冲击。如图3所示，五次B样条轨迹曲线，在满足机械手臂关节运动约束条件的基础上，不仅具有连续、平滑变化的速度、加速度、加加速度曲线，同时还由于其函数的特性可随时对部分检测轨迹进行局部调整而不影响整段轨迹，这是其他轨迹曲线都不具备的，所以结合上述分析从机械手臂运动动态、使用寿命、轨迹调整能力等方面考虑，五次B样条轨迹曲线作为五自由度串联机械手臂检测工件表面缺陷的检测轨迹是具有很大优势的。