一种基于随机仿真优化的反感知RGPO干扰方法

张泽锐,张天贤,陈锋彬,李健涛

(电子科技大学 信息与通信工程学院, 四川 成都 611731)

0 引 言

近年来,距离门拖引干扰(RGPO)因其被发现概率小、被感知识别风险低以及对雷达干扰效果显著等优点而受到广大研究者的青睐。然而,随着雷达有源欺骗干扰感知技术研究的深入[1-2],传统的匀速拖引策略和匀加速拖引策略越来越容易被识别,这就对干扰方所提供的干扰策略提出了更高的性能需求。

目前,RGPO干扰领域的工作主要集中在信号级上干扰信号的波形设计与生成[3-5],却忽视了在数据级上基于RGPO干扰策略的优化。实际上,数据级上基于干扰策略的优化不仅能够提升干扰成功率,并且能够降低拖引策略被敌方雷达感知识别的可能性,是一种极具研究价值的反感知RGPO干扰方法。文献[6-7]早就指出对时延的设置是影响RGPO干扰策略性能的主要因素,并定性分析了时延对RGPO干扰的影响。此后,利用优化算法对RGPO干扰中的时延设置进行优化成为了研究热点[8-11],文献[8]以平均波门偏移距离作为干扰效果的性能评价指标,建立了RGPO干扰的多帧联合优化模型,提出了基于粒子群优化(PSO)算法的RGPO干扰策略优化方法。文献[10]针对雷达跟踪系统干扰性能不足的问题,以粒子群优化算法为基础提出了一种RGPO干扰策略自适应生成方法。

然而,由于雷达跟踪过程中存在过程噪声和量测噪声,即使干扰策略是固定的,敌方雷达跟踪系统所产生的干扰结果仍然存在不确定性,使得衡量RGPO干扰策略的性能变得更加困难。并且,在真实的战场环境下,干扰方依赖侦察分析雷达发射信号来获得少量的雷达行为特征,准确获得敌方雷达跟踪效果的可能性极小,这就意味着干扰方将难以直接观察到敌方雷达跟踪系统对干扰结果的准确反馈。因此,RGPO干扰的策略优化并不是一个确定性的优化问题,而是一个随机仿真优化问题,现有的各种智能优化算法在随机优化环境下的性能还需要进一步的提升。

基于以上分析,本文首先将RGPO干扰的策略优化问题建模为一个随机仿真优化(SSO)问题,并设计了一个不依赖于敌方雷达跟踪系统信息的RGPO干扰策略评价方案。为了解决干扰策略性能评价的不确定性,可以利用重采样的方法得到干扰策略的评分均值,并以此评价该干扰策略的性能。本文将一种基于假设检验的计算预算分配算法与传统的粒子群优化算法结合,提出了一种基于假设检验的计算预算分配-粒子群优化算法(HTCBA-PSO)。最后,通过数值仿真的方式与PSO-ER、PSO-ERN[12]、PSO-OCBA[13]等传统随机仿真优化算法进行了比较,验证了该算法的有效性。

1 RGPO干扰策略优化模型的建立

1.1 RGPO干扰场景建模

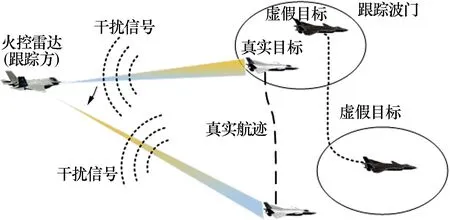
图1 RGPO干扰场景示意图Fig.1 Diagram of RGPO jamming

(1)

因此,在第k个干扰阶段,真实目标与假目标之间的距离dk可以表示为

(2)

式中:c代表光速。

设真实目标的状态方程为

X(k)=f[k,X(k-1)]+ψ[,X(k-1),v[X(k-1)]]

(3)

式中:X(k)表示第k个干扰阶段真实目标的状态向量;f[·]表示当前干扰阶段状态与下一干扰阶段状态之间的状态转换函数;v[·]表示过程噪声序列;ψ[·]表示过程噪声的分布函数。

(4)

式中:θ[·]是将dk投影到状态空间中的投影函数。此时,雷达跟踪系统对真实目标和假目标状态矢量的量测值可以分别表示为

Z(k)=h(k,X(k))+ω[k,X(k)]

(5)

(6)

式中:h[·]表示测量函数;ω[·]表示量测噪声序列。

一般来说,雷达跟踪系统的数据处理过程为

(7)

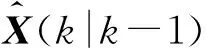
(8)

式中:φ[·]表示关联函数;(k)表示被怀疑来自被跟踪目标的量测集。由此可以得出雷达跟踪系统在第k个干扰阶段的状态估计为

(9)

1.2 基于随机仿真优化的RGPO干扰策略的优化模型

一般情况下,对RGPO干扰结果的评价主要取决于两点:

(1) 真实目标是否离开跟踪波门。

(2) 波门拖引距离(POD),即在有限的干扰阶段内RGPO干扰将雷达距离波门中心拖离真目标位置的距离。

在本文中对RGPO干扰策略性能的评价将基于以上两项指标进行。

首先,定义ξ(k)为真实目标在第k个干扰阶段是否摆脱跟踪波门

(10)

式中:ξ(k)=1表示真实目标已经摆脱跟踪波门,而ξ(k)=0表示真实目标还尚未摆脱跟踪波门。

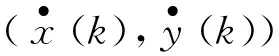
(11)

(12)

据此,定义第k个干扰阶段的拖引距离为

(13)

为了评价在最后一个干扰阶段K的RGPO干扰策略性能,干扰策略性能可以表示为以ξ(K)和拖引距离POD(K)为自变量的函数

(14)

式(14)中包含噪声和杂波序列,RGPO干扰策略的性能存在不确定性。因此,建立随机仿真优化模型为

(15)

式中:Ω代表决策空间。

1.3 干扰策略评价方案的优化

POD(k)属于敌方雷达跟踪系统信息,并不会在电子对抗中被干扰方轻易获取,因此,式(14)所表示的干扰策略评价方案要简化为一种对敌方雷达跟踪系统信息需求更小的评价方案。

一般情况下,干扰方可以通过在干扰停止时感知敌方雷达工作模式是否改变来判断真实目标是否已经摆脱跟踪波门。因此,对于干扰策略性能的评价可以据此分为以下两种情况:

(1) 如果真实目标没有摆脱跟踪波门,即ξ(K)=0,那么该干扰策略的评分将为0。

(2) 如果真实目标已摆脱跟踪波门,即ξ(K)=1,此时的干扰策略评分将取决于POD(K)。

(16)

式中:d1imit表示为防止异常干扰结果影响干扰策略平均性能而设置的参数。

2 RGPO干扰策略优化算法

2.1 算法整体架构

在本节中,图2展示了HTCBA-PSO的总体架构和基本原理。HTCBA-PSO的主体包括两个部分:PSO和基于假设检验的计算预算分配。其中,PSO主要用于搜索解空间并生成N个候选解[14],计算预算分配则主要负责分配有限的计算预算M来估计这些候选解的性能。

图2 HTCBA-PSO流程图Fig.2 Generic diagram of HTCBA-PSO

2.2 PSO粒子更新程序

在PSO的第t次迭代中,每个粒子的位置更新为

(17)

(18)

(19)

式中:tmax表示最大迭代次数,在这里取150;ωmax表示惯性权重的初始值,通常取0.9;ωmin表示迭代结束时的惯性权重值,通常取0.4。

2.3 基于假设检验的计算预算分配程序(HTCBA)

为了对PSO生成的候选RGPO干扰策略性能进行评价,本文采用重采样的方法对候选RGPO干扰策略进行性能估计。显然,采样次数越多,该候选策略的性能估计就越准确。但是在现实工程问题中,重采样次数是重要的计算预算资源,过多的重采样次数会加大时间和计算预算资源上的负担,因此重采样的次数是有限的。本节针对有限的计算预算资源分配问题,提出了一种基于假设检验的计算预算分配方法。

计算预算的分配分为多个阶段,首先,要将初始计算预算m0分配给PSO所生成的每个RGPO干扰策略,以获得下一个分配阶段中必需的的统计信息。在之后的每个阶段,都会根据特定的分配规则面向RGPO干扰策略分配增量计算预算Δ。为了构建一个更为合理的计算预算分配规则,引入了假设检验的相关理论。

(20)

(21)

由于自由度必须为整数,要对计算结果进行取整处理,

(22)

此时,该项假设检验的p值δij可以表示为

(23)

(24)

λb=max(δb,1,…,δb,o,…,δb,N)
(o∈{1,2,…,N},o≠b)

(25)

λo=δb,o(o∈{1,2,…,N},o≠b)

(26)

显然,将更多的计算预算分配给具有更高不确定度的干扰策略是选择最优RGPO干扰策略的关键,即不确定度越高的干扰策略将被分配更多的计算预算,因此,可以得到一个分配规则如式(27)所示。

(27)

3 仿真验证

为了评价HTCBA-PSO在RGPO干扰策略优化上的性能优势,假设跟踪目标在二维平面内作近似匀速(CV)运动,并在该跟踪场景下与其他优化算法进行了对比仿真验证。

3.1 仿真参数设定

假设跟踪目标从[50 km, 55 km]处出发,以[50 m/s, 350 m/s]的速度作近似匀速直线运动,跟踪目标在x轴方向上和y轴方向上的过程噪声均满足N(0.52);跟踪方雷达采用卡尔曼滤波的方式进行跟踪,其在距离向和角度上的量测噪声分别满足N(0,102)和N(0,0.001 752),在x轴方向上和y轴方向上的过程噪声均满足N(0,102),跟踪波门采用椭圆波门,波门参数γ设为16,量测落入波门内概率为0.999 7;干扰方的总拖引帧数为15,d1imit取900 m。

PSO的相关参数已在上一节中介绍。对于HTCBA而言,初始计算预算m0设为100,每一次PSO迭代中所要分配的总计算预算M设为10 000,每个分配阶段需要分配的计算预算Δ设为1 000。由于总计算预算数量有限,粒子群中粒子个数越多,分配给每个粒子的计算预算数量就越少。为了探究粒子个数对算法性能的影响,在本节的算法性能对比实验中粒子个数N将被分别设为40、20和10。

3.2 仿真分析

表1给出了PSO-ER[8,10]、PSO-ERN、PSO-OCBA[9]、HTCBA-PSO四种算法在50次Monte Carlo实验后所得到的最佳RGPO干扰策略的平均最优。

表1 平均最Tab.1

图3给出了PSO-ER、PSO-ERN、PSO-OCBA、HTCBA-PSO四种算法在上述仿真条件下,经过50次Monte Carlo实验后所得到的最佳RGPO干扰策略的平均迭代曲线。

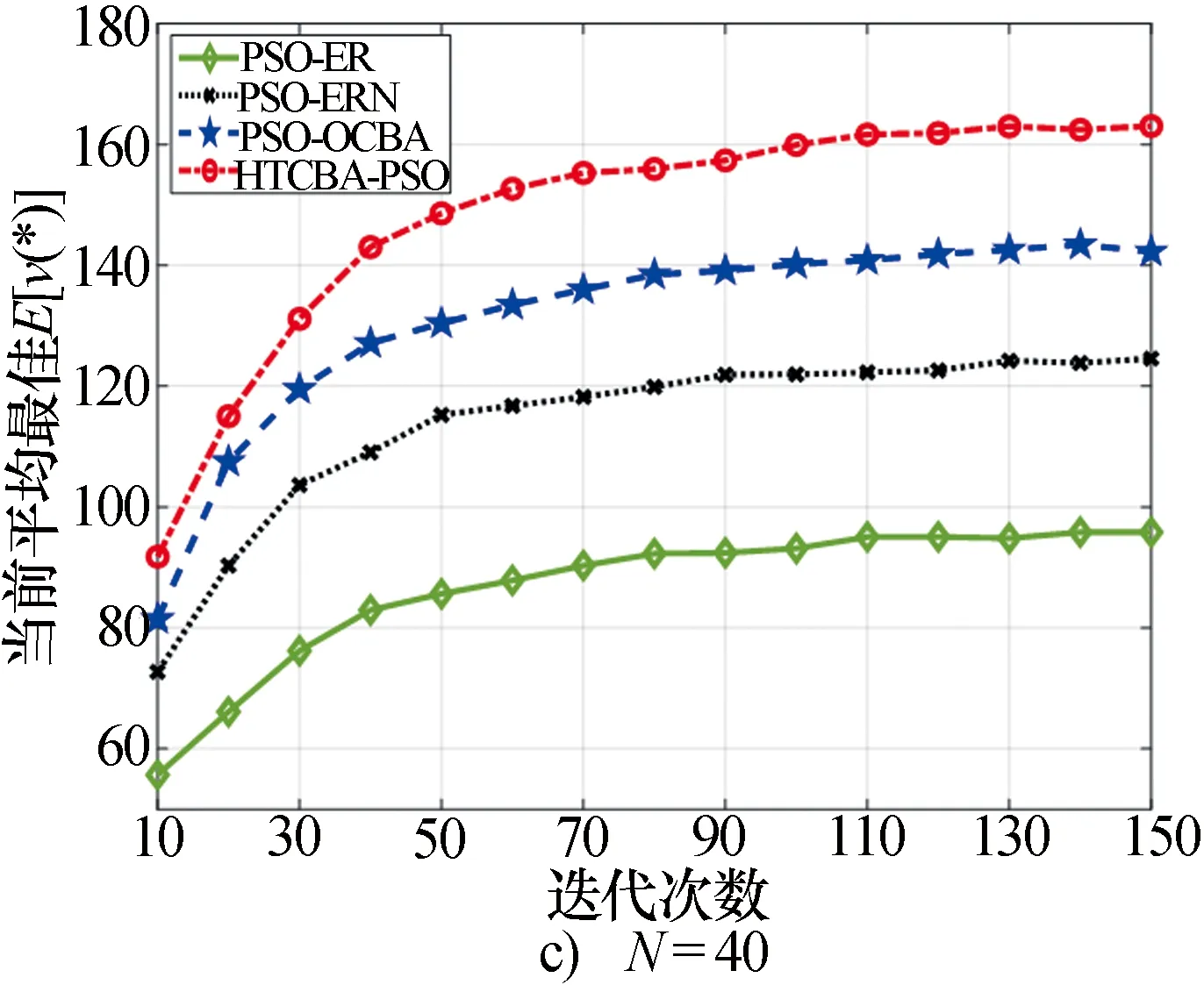
图3 三种情况下的平均迭代曲线Fig.3 Average iteration profile of

从图3中可以发现,当从10变化到40的过程中,HTCBA-PSO的性能均优于其他三种算法。同时结合对表1结果的分析可知,当N=10或N=20时,HTCBA-PSO的初始性能较差,但是随着迭代次数的增加,HTCBA-PSO所得到的RGPO干扰策略性能迅速提高,当N=40时,HTCBA-PSO的初始性能良好,但是性能曲线的提升速度却小于N=10或N=20的情况。这是因为在N比较小时,HTCBA-PSO本身的搜索能力较弱,导致在迭代初期对解空间的搜索不足。因此,有限的计算预算能够分配给更少量的候选解,提升RGPO干扰策略性能的估计准确性。因此,性能曲线会随着迭代次数的增加而迅速提高。但是,这仍然无法弥补在N=10或N=20的情况下HTCBA-PSO对解空间的探索能力不足的问题,所以HTCBA-PSO在N=40时得到的RGPO干扰策略的平均性能要优于其他情况。

上述结果已经可以证明基于HTCBA-PSO的RGPO干扰策略优化算法的性能优于其他算法。但是,通过HTCBA-PSO所得到的RGPO干扰策略的具体干扰效果还需要通过实验加以验证。因此,本文将利用POD和拖引成功率(POR)两项评价指标来测试N=40时通过HTCBA-PSO所得到的RGPO干扰策略的具体干扰效果。传统的匀速拖引策略和匀加速拖引策略就是让假目标相对于真目标做匀速运动或匀加速运动来达到拖引波门离开真目标的目的。为了增加对比效果,本文也展示了传统的匀速干扰策略和匀加速拖引干扰策略在CV场景下的具体干扰效果。

图4绘制了在拖引速度取154 m/s的情况下,匀速拖引策略在CV场景下的POD箱线图和POR曲线。通过观察可知,在匀速拖引策略下,POD箱线图在最后一帧的上四分位数可以达到383 m;POR在最后一帧可以达到15.04%。

图4 匀速拖引策略在CV场景下的POD箱线图和POR曲线Fig.4 Simulation results of POD and POR for uniform velocity pull-off jamming strategy over different jamming stages on CV benchmark

图5绘制了在拖引初速度取86 m/s,加速度取64 m/s2的情况下[9],匀加速拖引策略在CV场景下的POD箱线图和POR曲线。

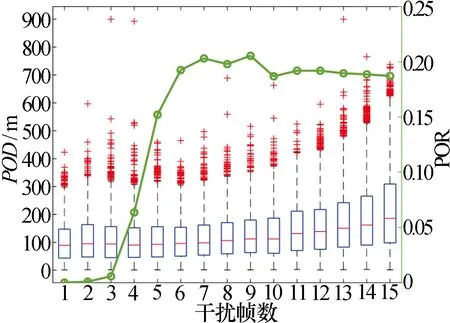
图5 匀加速拖引策略在CV场景下的POD箱线图和POR曲线Fig.5 Simulation results of POD and POR for uniform acceleration pull off jamming strategy over different jamming stages on CV benchmark

通过观察可知,在匀加速拖引策略下,POD箱线图在最后一帧的上四分位数可以达到626 m;POR在最后一帧可以达到18.72%。图6绘制了在HTCBA-PSO所生成的RGPO干扰策略下的POD箱线图和POR曲线。由图6中的箱线图可知,随着干扰帧数的增加,POD的箱线图逐渐发散,其上四分位数最终可以达到725 m。与此同时,随着干扰帧数的增加,POR不断增加,最终达到了接近25%的拖引成功率。然而,在第9帧和第13帧却出现了在POD持续上升的情况下,POR不升反降的情况。这主要是因为在POR较前一帧有了较大提升的情况下,进一步增大POD将可能会降低干扰量测值落入跟踪波门的概率,从而导致了POR的下降。将图6中的两项拖引干扰性能指标与图4、图5对比可知,在HTCBA-PSO所生成的RGPO干扰策略下,POD提升了17.69%,POR提升了9.96%。

图6 N=40时HTCBA-PSO所得到的RGPO干扰策略在CV场景下的POD箱线图和POR曲线Fig.6 Simulation results of POD and POR for the RGPO jamming strategy obtained by HTCBA-PSO at N=40 on CV benchmark

上述结果表明,在HTCBA-PSO所生成的RGPO干扰策略下,被攻击敌方雷达跟踪系统的可靠性显著降低。同时,干扰效果随着干扰帧数的增加而逐渐增加,这也与RGPO干扰的原理一致。

4 结束语

本文针对随机优化环境下RGPO干扰策略优化问题,提出了一种基于HTCBA-PSO的RGPO干扰策略优化算法。首先,通过对雷达跟踪过程的分析,将RGPO干扰策略优化问题建模为一个SSO问题,为了解决干扰方难以获得敌方雷达跟踪系统信息的问题,提出了一种不依赖于敌方雷达跟踪系统信息的RGPO干扰策略评价方案;然后,为了提升传统算法在解决SSO问题时的性能,提出了一种基于HTCBA-PSO的RGPO干扰策略优化算法;最后,在跟踪目标做近似匀速运动的背景下,选择不同种群规模来验证HTCBA-PSO的有效性,并通过POD和POR两个物理量来验证通过HTCBA-PSO所得到的RGPO干扰策略的具体干扰效果。仿真结果表明:在不同种群规模下,HTCBA-PSO的性能均优于其他三种算法,并且与传统算法相比,本文提出的优化方法能提高干扰方的波门拖引距离和拖引成功率,这对于在电子对抗环境下的反感知RGPO干扰研究具有重要意义。