KL散度多模块滑动窗口慢特征分析的故障诊断方法
2023-12-08郭昕刚霍金花许连杰
郭昕刚,霍金花,程 超,许连杰
(长春工业大学 计算机科学与工程学院, 吉林 长春 130012)
随着现代工业的发展,数据驱动方法在过程监控中发挥着重要作用[1-2]。在主流方法中,多元统计过程监控(multivariate statistical process monitoring,MSMP)被用于监控多元复杂工业过程中的故障[3]。传统的多元统计监控主要包括主成分分析法(principal component analysis,PCA)、偏最小二乘法(partial least square,PLS)和独立成分分析[4](independent component analysis,ICA)。
工业过程的复杂性和未知的动态特性使得静态过程的监测效果较差。传统的MSMP方法是静态过程监控方法,即当前时间的样本与过去的样本没有关联,样本数据相互独立,忽略了动态特性。Li等提出了一种部分动态主成分分析(dynamic principal component analysis,DPCA)来提高动态过程监测能力[5]。针对过程动力学和数据非高斯统计的特点,动态独立成分分析(dynamic independent component analysis,DICA)也相继被提出[6-7]。上述方法以消除动力学为目标,往往假设所有变量具有相同的动态特性,然后对原始数据进行扩展,与传统方法相比提高了性能,但产生了大量的冗余信息,处理动态特性较强的变量时性能较差。慢特征分析[8](slow feature analysis, SFA)可以从时间序列中提取缓慢变化的特征,表征变量变化的快慢程度,是一种有效的无监督算法。Shang等提出了基于SFA的动态监控,实现了运行和控制性能的监控[9]。上述方法虽然克服了动态缺陷,但只建立单一模型却忽略了局部信息,导致大规模工业过程的诊断性能较差。
多模块算法最早由Macgregor等提出,有效利用局部信息改进过程分析将整个模型分为多个子模型[10]。Ge等根据主成分分析的不同方向对原始数据进行划分,将线性变量分配到同一个块中,分块过程中存在缺失和重叠的问题[11]。Tong等分别分析了变量与主元子空间和残差空间的相关性,再将变量分配到相应的子空间中实现分块[12]。这些方法都以先验知识作为前提,极大程度限制了该方法的应用。KL(Kullback-Leibler)散度作为一种新的概率测度,可以测量两个统计变量之间的差值,用来解决故障诊断问题[13-14]。Wang等利用KL散度将具有类似统计特征的变量划分为一块,在每个低维子空间中建立PCA模型,使用贝叶斯策略进行融合[15]。周伟等在DPCA建模的基础上,利用 KL 散度量化模型得到分向量概率分布之间的相似度,从而建立多块模型实现对微小故障的诊断[16]。
在实际的工业生产过程中,大多数缓慢变化的过程数据也具有非线性时变的特性,其使正常数据出现偏移,导致出现误警现象。柯亮等提出了基于滑动窗PCA的微小故障检测方法,利用滑动窗口的策略对数据实时更新,使得故障数据与非故障数据分化明显,实现了对微小故障的放大,提高了模型的自适应能力[17]。
综合以上问题,提出一种基于KL散度的多模块滑动窗口慢特征分析故障诊断方法,利用KL散度的统计特性,建立多块模型,在每个块中应用SFA来提取过程数据的不同动态,利用滑动窗口得到最优模型,克服依据先验知识分块的策略、单一模型不稳定等问题。在田纳西伊斯曼(Tennessee Eastman, TE)过程监控中取得了较好的诊断效果。
1 理论基础
1.1 KL散度
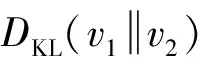
(1)
由于KL散度的定义具有不对称性,不能作用于距离的度量。 在实际的应用中,人们将其改进为对称形式
(2)

1.2 慢特征分析
假设存在m维时间序列输入信号x(t)=[x1(t),x2(t),…,xm(t)]T, SFA的目标是找到一组特征函数g(t)=[g1(t),g2(t),…,gm(t)]T,使得特征s(t)=g(x(t))缓慢变化[2]。s(t)=[s1(t),s2(t),…,sm(t)]T用来表示缓慢变化的特征,SFA的优化问题表示如下
(3)
约束条件为
〈si〉t=0
(4)
(5)
∀i≠j,〈sisj〉t=0
(6)
线性SFA中,每个缓慢变化的特征(slow features, SFs)是所有输入数据的线性组合
s=Wx
(7)
式中,W=[w1,w2,…,wm]T是权重矩阵。
R=〈x(t)x(t)T〉t=UΛUT
(8)
式中,U是R的特征值,Λ是由特征值组成的对角矩阵。白化矩阵可表示为Q=Λ-1/2UT,白化过程为
z=Λ-1/2UTx=Qx
(9)
结合式(7)和式(9),SFs进一步表示为
s=Wx=WQ-1z=Pz
(10)
式中,P=WQ-1,〈zzT〉t=Q〈xxT〉QT=I,〈z〉t=0。优化问题(3)和约束条件进一步表示为
(11)
(12)
(13)
(14)
为了满足式(11)~(14),优化问题再次转化为求解正交矩阵P。
(15)
式中,P=[p1,p2,…,pm]是正交特征向量矩阵,对应的特征值为Ω=diag(λ1,λ2,…,λm),且λ1≤λ2≤…≤λm。
权重W表示为
W=PQ=PΛ-1/2UT
(16)
最后,得到m个缓慢程度由大到小排列的SFs。
s=Wx=PQx=PΛ-1/2UTx
(17)
(18)
2 基于KL散度多模块滑动窗口慢特征分析方法及过程监测
2.1 KL散度分块策略
使用KL散度度量任意两个变量间的相关性,并进一步构造KL散度分量,作为分块的基础。
对于训练数据X=[x1,x2, …,xm]T∈Rn×m,m和n表示变量数和样本个数。取任意两个变量xi和xj,且xi∈X,xj∈X,在正态分布的条件下,KL散度分量表示为
(19)

(20)
最后将训练数据分成两个子模块X=[x1,x2, …,xm]T= [X1,X2]T。
2.2 多模块滑动窗口慢特征分析方法
根据工业过程的动态特性,将子模块X=[X1,X2]T扩展d个时延,使当前样本与过去样本相关联,得到增强的过程矩阵,在SFA建模过程中扩展了动态特性,矩阵增强过程如式(21)所示。
(21)
式中,i是子模块数量,n是过程变量的样本量。
随后进行SFA离线建模,局部建模过程中使用滑动窗口算法训练最优的离线模型,如算法1所示。

算法1 滑动窗口训练最优模型
以上模型通过将样本数据根据欧氏距离升序排列,使用滑动窗口算法对样本进行筛选,得到最优的局部模型及相应的权重矩阵W1,W2,提高了模型的自适应能力。
为了实现对故障的检测,分别构造T2和S2统计量对故障进行在线监测,T2表示统计量在慢特征空间中的静态变化,S2表示过程统计量的动态变化分布。T2统计量定义为
(22)
(23)
其中,子块的SFs为si=Wixi,i=1,2。S2统计量定义为
(24)
(25)
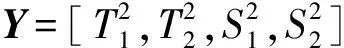

算法2 SVDD建模及监测
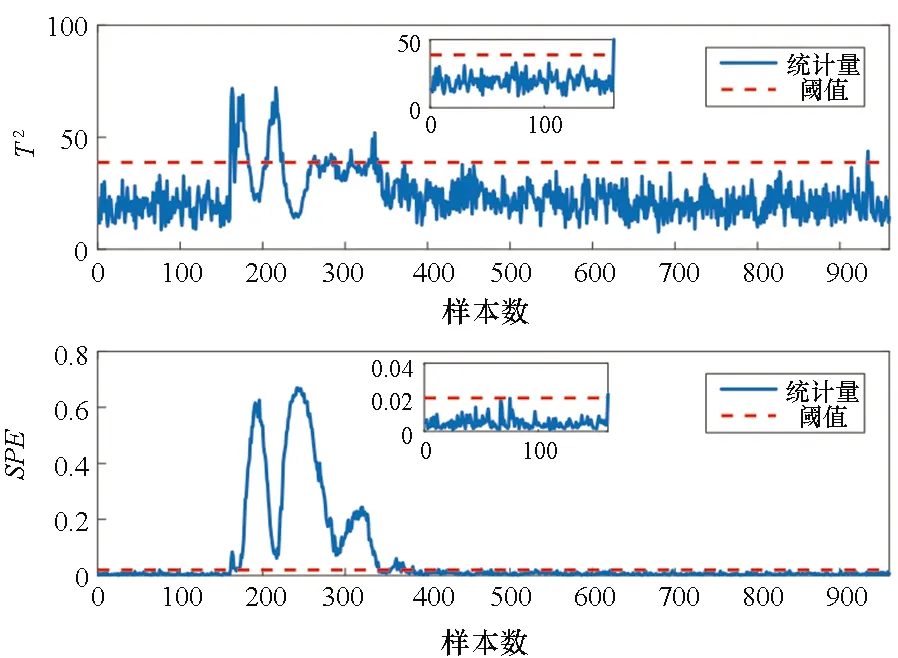
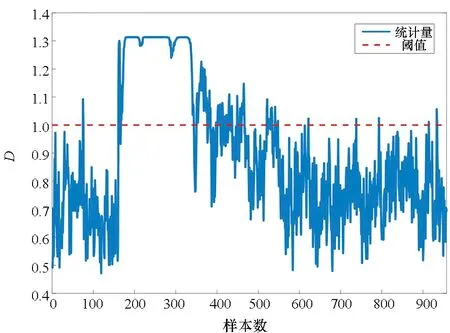
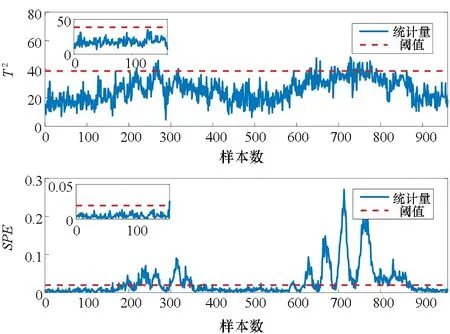
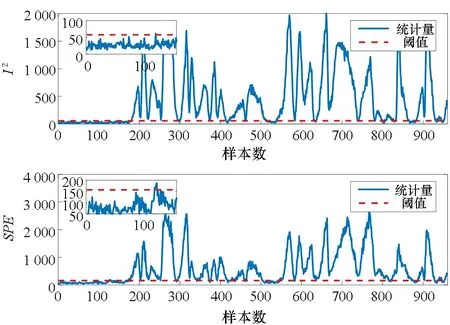
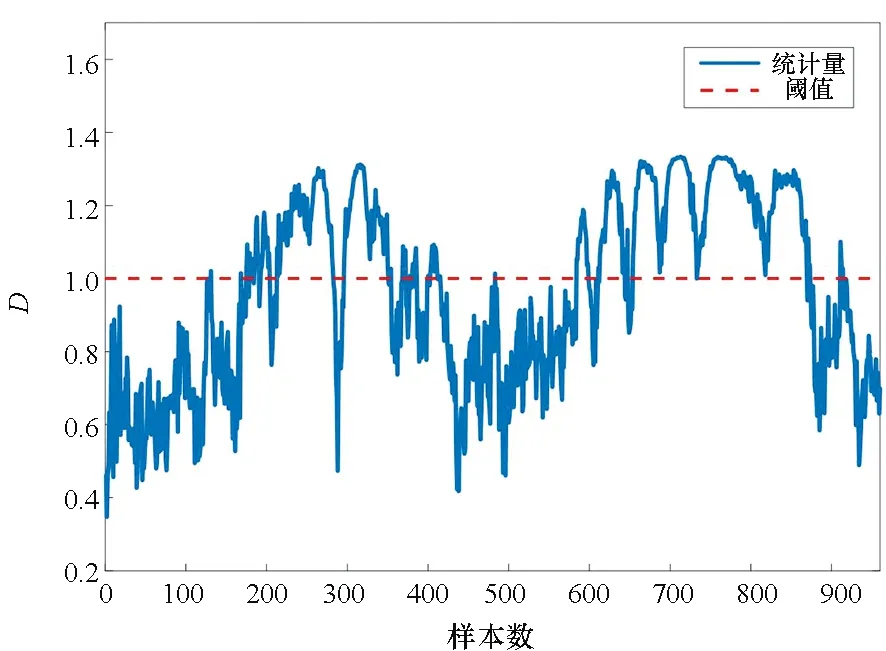
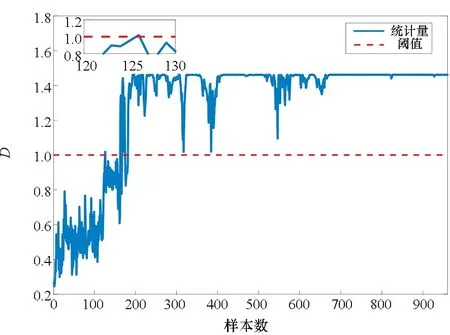
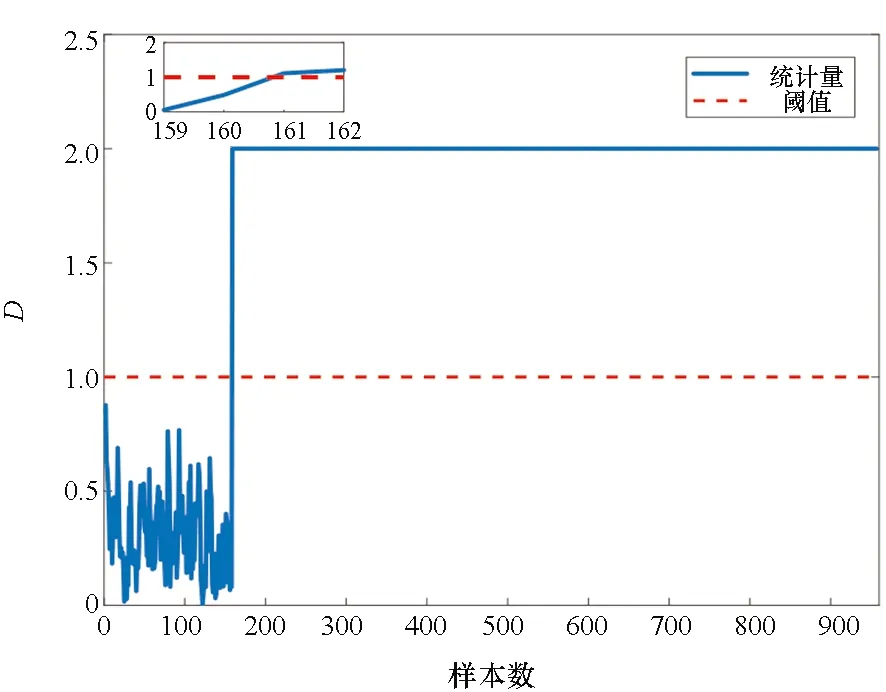
监测结果融合后,得到阈值控制限Dt=1和半径中心DR。当D≥Dt时,检测出故障,反之D 基于KL散度的多模块滑动窗口慢特征分析方法(multi-block moving window slow feature analysis method based on KL divergence,KL-MWSFA)的过程监测详细步骤如下。 离线训练: 步骤1:对训练数据X标准化,计算变量间的KL散度分量dKL。 步骤2:随机取dKL中的两个值作为中心,根据损失函数依次迭代更新中心数值,直到收敛,划分为两个子块X=[X1,X2]T。 步骤3:将子块进行d个时延扩展为动态矩阵,计算与测试数据的欧氏距离,将其升序排列。 步骤4:利用滑动窗口对每个子块进行SFA离线建模,分别计算T2,S2的阈值。 在线监测: 步骤5:对故障数据标准化,扩展d个时延,然后分块。 步骤6:使用SFA进行训练,得到T2,S2的阈值,作为SVDD的输入Y。 步骤7:建立SVDD模型,计算测试向量Yt到超球半径的距离,得到DR。 步骤8:控制限Dt=1,当D≥Dt时,发生故障,反之正常。 TE过程是美国化工公司在大量实际工程经验的基础上,由Downs和Vogel[19]提出的一个化工过程模型,其产生的数据具有时变性、强耦合性以及非线性,广泛应用于过程控制、监测和故障诊断研究,工艺流程如图1所示。主要由反应器、冷凝器、压缩机、气液分离器以及汽提塔5个操作控制部分构成。其共有33个变量,正常情况下的基准数据集包含500个样本。故障数据共有960个样本,前160个是正常数据,第161到960个样本为故障数据。本实验选择22个过程变量和11个操作变量作为输入,用500个正常样本建立模型。仿真共有21个故障类型,其中16种是已知故障,剩余5种是未知故障,实际的建模和监测过程中,一般不包括由搅拌速度引起的故障21,故采用15种已知故障进行测试,具体描述如表1所示。 图1 TE过程流程图Fig.1 TE process flow chart 表1 TE过程故障类型表 随机选取两个变量作为初始中心,计算KL散度分量构成的对称矩阵到初始中心的欧氏距离,离初始中心最近的分量重新确定为新的中心,依次迭代,最后收敛时将变量自动分成两个子块。具体分块策略见第2.1节,变量间的分布如图2所示,分块结果如表2所示。 将KL-MWSFA和核主成分分析(kernel (a) 聚类前的变量分布(a) Distribution of variables before clustering principal component analysis, KPCA),ICA,SVDD进行对比分析,故障检测率如表3所示,可以看出,对于故障1,2,4,5,6,7,8,9,10,11,12,13,KL-MWSFA方法都能有效检测到这些故障。由于故障3,9,15的震级非常小,几乎所有的方法都无法检测到故障。但对于故障5,10,12,该方法具有较好的检测性能。 故障5是冷凝器冷却水入口温度的阶跃变化,导致冷凝器温度发生变化[20]。故障5的监测图如图3所示,图3(a)在第300个采样点以后,无法检测出故障。图3(b)I2统计量在第161个采样点之前发生虚警现象,图3(c)在故障正常检测一段时间后,大部分统计量向控制限下方波动,检测效果一般。图3(d)在第161个采样点检测到故障后,一直持续到最后一个样本,检测效果较好。 表3 KPCA,DICA,SVDD和KL-MWSFA的故障检测率Tab.3 Fault detection rate of KPCA, DICA, SVDD and KL-MWSFA (a) KPCA监测结果(a) Monitoring results of KPCA (b) DICA监测结果(b) Monitoring results of DICA (c) SVDD监测结果(c) Monitoring results of SVDD (d) KL-MWSFA监测结果(d) Monitoring results of KL-MWSFA图3 故障5监测结果Fig.3 Monitoring results for fault 5 故障10是C进料温度的随机变化,主要影响汽提塔压力[21]。图4为KPCA,DICA,SVDD和KL-MWSFA的监测图,图4(a)的T2统计样本大部分在控制限下面,检测效果不佳,图4(c)的监控数据在控制限附近波动,也无法清楚地检测到故障的发生,由表3可见DICA和KL-MWSFA检测效果较好,但在图4(b)的子图中,我们可以看到个别正常样本出现虚警,只有图4(d)在检测故障的同时没有发生虚警状况。 故障12是冷凝器冷却水入口温度的随机变化[22]。由图5(a)可知,T2监测性能不好且在阈值附近上下波动,图5(b)虽然可以检测到故障,但在正常工况时发生虚警,图5(c)在发生虚警的同时监测效果没有图5(b)的效果好,而图5(d)的监测性能在检测中均得到改善,没有虚警并检测到所有故障。 (a) KPCA监测结果(a) Monitoring results of KPCA (b) DICA监测结果(b) Monitoring results of DICA (c) SVDD监测结果(c) Monitoring results of SVDD (d) KL-MWSFA监测结果(d) Monitoring results of KL-MWSFA图4 故障10监测结果Fig.4 Monitoring results for fault 10 (a) KPCA监测结果(a) Monitoring results of KPCA (b) DICA监测结果(b) Monitoring results of DICA (c) SVDD监测结果(c) Monitoring results of SVDD (d) KL-MWSFA监测结果(d) Monitoring results of KL-MWSFA图5 故障12监测结果Fig.5 Monitoring results for fault 12 本文提出了一种基于KL散度的多模块滑动窗口慢特征分析方法,该方法使用KL散度算法度量每两个变量间的相似度,利用最小误差平方和准则对变量间的距离依次迭代,实现了对样本的无监督分块,并在每个子块中建立SFA监测模型,解决了单一模块的不稳定性问题,同时引入滑动窗口建立最优子模型,利用SVDD将子块监测结果融合。并将所提方法应用于TE过程,验证了该方法的有效性。2.3 KL-MWSFA过程监测
3 TE过程仿真实验
3.1 TE过程简要介绍
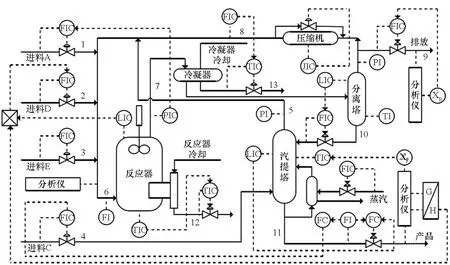

3.2 分块
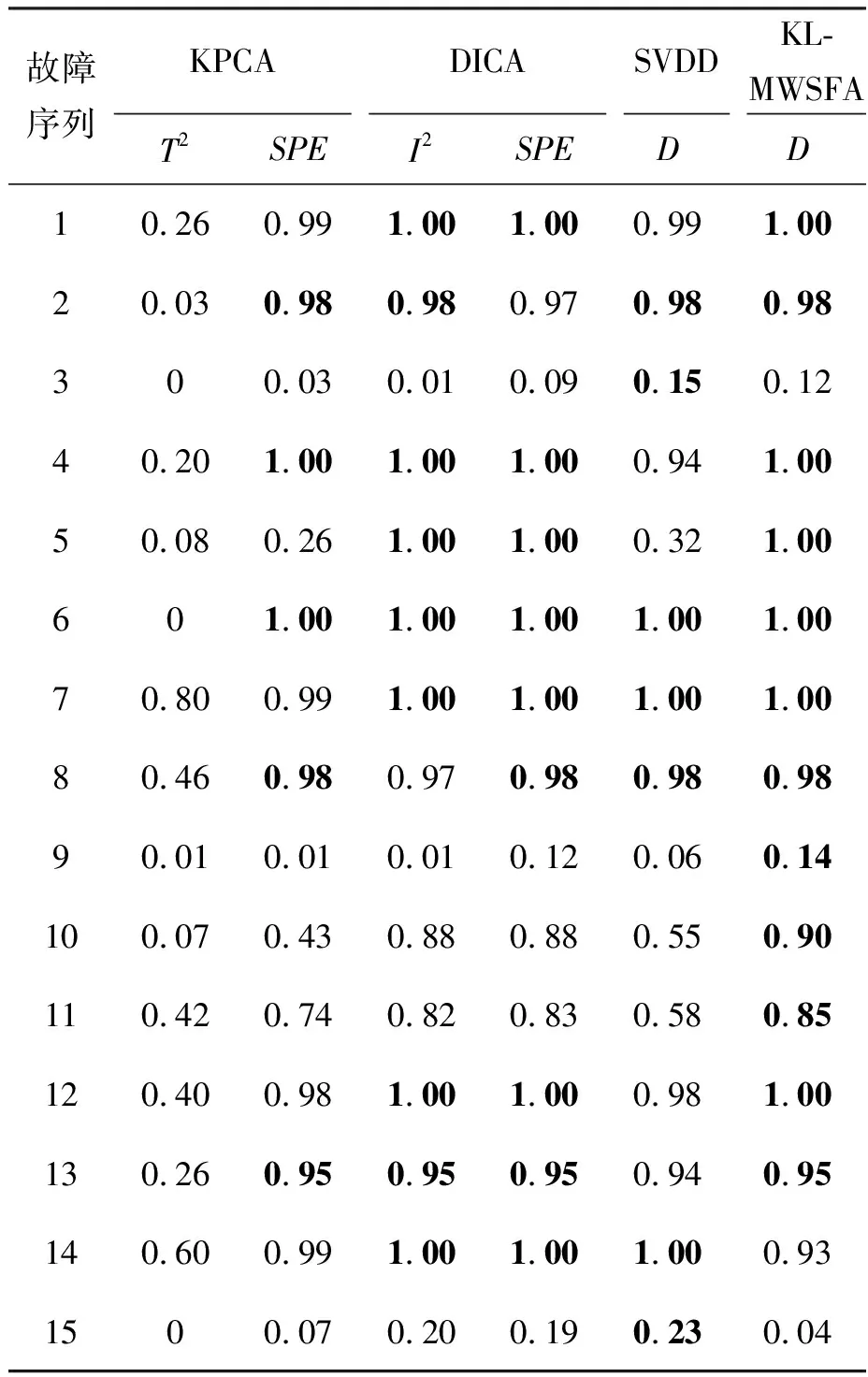
3.3 TE仿真实验结果分析






4 结论
