面向飞行器电磁散射特征诊断的近场频域成像算法
2023-12-08贾高伟
贾高伟,阴 鹏,邵 帅
(国防科技大学 空天科学学院, 湖南 长沙 410073)
飞行器的雷达隐身性能,已经成为先进飞机的重要指标。[1]
无人飞行器没有飞行员座舱、生命维持系统的约束,其机身结构尺寸可以更小,结构形式可以更为灵活,结构材料也可以更为多元化。鉴于飞行器结构样式与材料构成与雷达隐身性能密切相关,无人飞行器在结构和材料方面具有的灵活性,使得无人飞行器相对于有人机具有更大的隐身性能优化空间。但也须重视,无人飞行器具备的更为先进的复合材料、更为精细的外形结构使得基于缩比模型的测量与评估精度变差,而外场全尺寸实物测试存在成本高昂、保密性差、精度受限、易受天气影响等特点,不利于无人飞行器保持成本低廉、研发周期短等优势。因此,在室内或者室外的较小区域内开展全尺寸无人飞行器的近场测量,成为无人飞行器雷达散射特征分析的重要趋势[1-2]。综合上述分析得知,飞行器的极低雷达散射截面(radar cross section, RCS)设计与研制以及更为复杂工况下的RCS评估均需要近场测量技术的支撑。
事实上RCS是在远场条件下衡量目标电磁散射特性的物理量。在近距离开展RCS测量,电磁波不满足远场条件,此时的测量被称之为近场RCS测量。近场测试的核心技术是将近场测量数据转换(亦称外推)为远场数据,并得到RCS。从机理上看,数据外推一般可分为两种技术路线:基于成像原理的外推技术和基于成像结果的外推技术[3]。基于成像结果的外推技术处理流程简洁,且可获得雷达图像用于散射特征诊断,是当前研究热点。从实现过程看,它可以包含两个阶段,首先是近场成像,然后是基于成像结果的RCS外推。
在基于远场假设(即平面波假设)的成像中,根据回波信号模型,回波数据可直接看作图像的谱域采样。因此成像过程可直接经坐标变换或插值后利用逆傅里叶变换实现。具体地,若以ISAR二维成像模式为例,以目标中心为原点建立极坐标系,某一散射点的RCS可以表示为σ(ρ,φ),ρ为目标相关圆心距离,φ为角度。一般地,成像过程可以表述为:
(1)
式中,f是辐射频率,θ是成像积累角,EF(f,θ)是远场回波数据,ξ(f,θ,ρ,φ)为成像因子。由式(1)可知,像σ(ρ,φ)与回波EF(f,θ)之间满足傅里叶变换关系,即σ(ρ,φ)⟺EF(f,θ)。
近场条件下,受球面波几何特征的影响,成像问题变得复杂。回波信号模型中相位与目标坐标位置不再是简单的由波数决定的线性关系。因此回波数据不能直接看成图像的谱域采样,而需经过更多的相位补偿和插值操作。但终究能够通过近场回波数据EN(f,θ)得到目标的像σ(ρ,φ)。这样通过像σ(ρ,φ)就建立了近场回波与远场回波之间的联系[3]。
基于上述介绍可知,近场成像的结果十分重要,直接影响RCS的外推,且近场成像结果能够以图像的形式直观地展示目标强散射点,在飞行器的设计、研制、定型、生产与使用过程中均具有重要意义。
结合成像理论可知,雷达天线相对目标的运动轨迹决定了成像算法的选择。当雷达天线相对于目标做直线运动时,传统的SAR成像算法[4],如尺度变标算法(chirp scaling algorithm, CSA)、频率变标算法(frequency scaling algorithm, FSA)以及距离徙动算法(range migration algorithm, RMA)等均考虑了球面波前的影响,因而可以直接应用于近场条件下的精确成像。
但当扫描方式不是直线轨迹时,如转台成像,则上述算法均不再适用。转台成像是指雷达收发天线不动,目标放置在转台上并沿方位向旋转,该模式使用方便,易于实现对目标360°全方位的电磁散射测量,是评估飞行器电磁散射特性的常用测量模式。按照目标距离天线位置的不同,转台成像又可分为近场条件和远场条件两类典型模式。
针对远场条件下的转台成像,高效率的成像算法包括距离多普勒算法(range Doppler algorithm, RDA)和极坐标格式算法(polar format algorithm, PFA)。RDA适用于小转角成像,在观测时间内散射点的走动不超过一个分辨单元的情况下[5],所获得的频率域目标信号的极坐标数据可近似被认为是直角坐标网格上的数据,对距离和方位向的数据分别进行傅里叶变换即可得到目标的雷达图像。PFA对RD算法成像性能进行了拓展,不再将小角度的极坐标数据近似为直角坐标上的数据,而是通过极坐标采样将数据插值到具有均匀栅格的直角坐标系中,再利用二维傅里叶变换得到目标图像[6]。
针对近场条件下的转台成像,现有的成像算法大多是时域算法。包括时域相关(time domain correlation, TDC)法、后向投影算法(back projection algorithm, BPA)等[4],时域成像算法通常能够适用各类成像几何模型,但其不足是计算量大,成像用时长,对成像处理器要求高。频域处理算法方面,Soumekh提出了一种基于系统核函数共轭转置的波前重建算法[7]。该算法是基于傅里叶变换及匹配滤波的成像算法,其成立的理论条件是系统核函数满足正交性,能够实现斜距平面频谱向地平面频谱的精确投影。但当雷达辐射信号为宽带信号且成像场景较观测半径更大时,基于系统核函数共轭转置的频谱投影会带来相位误差,导致成像失败。概括地说,针对近场条件下的转台成像,现有的频域成像方法仍不成熟,急需新的成像方法在确保成像质量的前提下提高成像效率,这对快速完成相关飞行器的雷达散射特征诊断具有重要意义。
本文基于转台成像几何模型,以线性调频信号为辐射信号,建立了近场成像通用回波模型,基于驻定相位原理得到回波二维频谱解析形式,分析了近场条件下转台成像频域处理的难点,并结合工程实际,提出了近似处理方法。本文的工作着重分析近场条件下的转台成像频域算法,暂不涉及RCS校正与外推。
1 转台成像通用模型
1.1 转台成像几何模型与通用回波模型
转台成像中目标放置于转台之上,雷达收发机及天线固定,雷达天线相位中心(antenna phase center, APC)对应转台中心的下视角为θZ。根据雷达运动-目标不动与雷达不动-目标运动的等效性,该成像模型如图1所示。
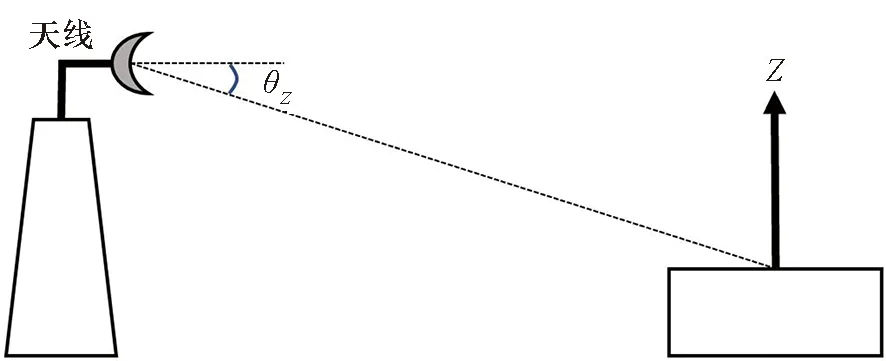
图1 转台成像结构示意图Fig.1 Structural diagram of rotating imaging
对于飞行器目标而言,其电磁散射来自局部效应的散射中心,且多散射中心的矢量合成散射场和雷达散射截面同理论计算得到的散射场以及雷达散射截面吻合较好[8]。本文开展的成像算法分析同样基于散射点模型,考虑的成像策略是在一定角度内相干积累并假定在该积累角范围内散射点具有恒定的散射特性。成像算法致力于实现成像结果中散射点正确的空间位置分布与良好的聚焦质量。相关的成像几何模型定义为:
图2中H代表APC相对于转台的高度,R代表雷达APC与转台中心的水平距离,等效为APC运动半径,Ra代表转台上放置目标的最大半径。设雷达APC相对转台中心的旋转角为θ,相对于转台中心O,雷达APC的三维极坐标为(R,θ,H),可以定义xr=Rcosθ,yr=Rsinθ,则APC的笛卡尔坐标为(xr,yr,H)。不失一般性,设定转台上某散射点P坐标为(r,φ,0),可以等价表示为(x,y,0),其中x=rcosφ,y=rsinφ。
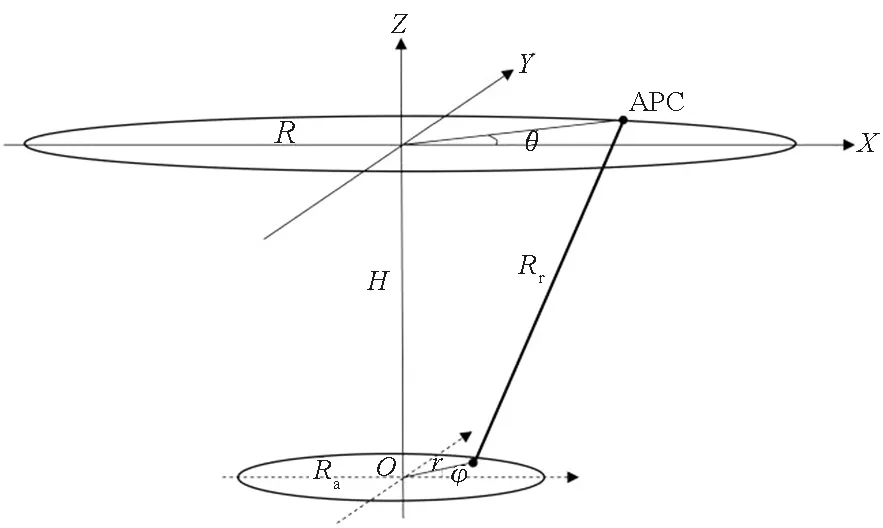
图2 具体的近场转台成像几何模型Fig.2 Detailed imaging geometry model of near-field rotating imaging
基于图2所示成像几何模型,可以得到雷达APC同目标P之间的瞬时斜距为:
(2)
设雷达发射信号为线性调频(linear frequency modulated, LFM)信号:
(3)

(4)

1.2 回波频谱特性解析分析
对式(4)沿方位观测角θ进行傅里叶变换,可以得到:
S(k,ξ)
exp(-jξθ)dθ
(5)
式中,ξ为方位角度域波数,为简便计,下文均称之为角度波数。
针对式(5),基于驻定相位原理,可以通过求解式(6)来获取对应的驻定相位点[10-11]。
(6)
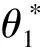

(7)
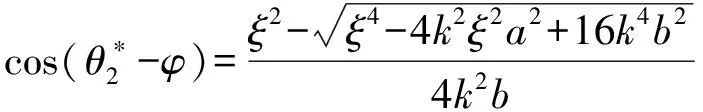
(8)
由此可知,转台成像回波对应两个驻定相位点,其频谱由两部分组成,这同圆周SAR的信号频谱是相似的[11],这也是转台成像在频域实现的难点所在。将由式(7)、式(8)求解得到的驻定相位点代入式(5),可以得到转台成像模式下雷达回波频谱在(k,ξ)域的表示形式为:
S(a,b,k,ξ)=SⅠ(a,b,k,ξ)+SⅡ(a,b,k,ξ)
(9)
式中,SⅠ(a,b,k,ξ)和SⅡ(a,b,k,ξ)分别为不同驻定相位点对应的子频谱[11]。
(10)
针对SⅠ(a,b,k,ξ)和SⅡ(a,b,k,ξ),可以分别构造对应的水平面频谱形式:SⅠg(a,b,k,ξ)和SⅡg(a,b,k,ξ),记为:
(11)
结合圆周SAR成像方面的研究成果[10],将斜距平面对应的频谱转换为水平面频谱是关键环节,后续的成像处理可以通过频域处理高效率完成。一种朴素的处理思想是对SⅠ(a,b,k,ξ)和SⅡ(a,b,k,ξ)分别进行相位补偿ΩⅠ(a,b,k,ξ)和ΩⅡ(a,b,k,ξ),即可得到SⅠg(a,b,k,ξ)和SⅡg(a,b,k,ξ)。
将SⅠg(a,b,k,ξ)与SⅡg(a,b,k,ξ)通过因式分解,总的频谱形式Sg(R,r,k,ξ)可以重写为:
Sg(R,r,k,ξ)
=SⅠg(a,b,k,ξ)+SⅡg(a,b,k,ξ)
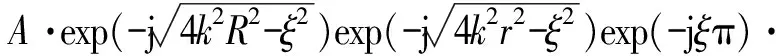
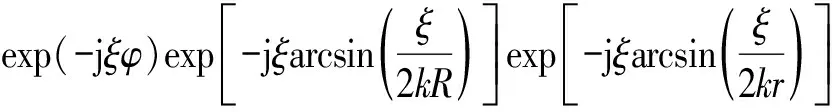
(12)
但在实际的相位补偿处理操作中,需要获知相位项ΩⅠ(a,b,k,ξ)和ΩⅡ(a,b,k,ξ)的解析表达式。以ΩⅠ(a,b,k,ξ)为例,理论上它的取值等于SⅠ(a,b,k,ξ)与SⅠg(a,b,k,ξ)的相位差,对比观察式(10)和式(11)可知,ΩⅠ(a,b,k,ξ)项与目标半径r以及角波数ξ有关,那么ΩⅠ(a,b,k,ξ)项的补偿将是距离及角度空变的,精确的相位补偿效率将很低。一种工程化的处理思路是针对飞行器的近场成像,重点考虑成像几何模型的特殊性,引入近似条件,简化处理流程。
结合图1,常规飞行器一般是纵横向较大,高度向较小,雷达APC与转台高度差不大,即H值通常较小[12];飞行器结构复杂,一般不满足散射中心各向同性且无迁移现象,其RCS具有明显的方位空变性。本文分析的前提是散射点在一定成像积累角度内具有恒定的散射特性。若成像积累角过大,则散射特性恒定的假设不再成立[13-14],因此有必要约束成像的积累角。
上述关于成像几何模型特殊性的描述可以等价为:θz较小且成像积累角Θ较小。在这样的成像约束下,结合美国Howland公司[15]以及意大利IDS公司开发的RCS近场测量系统[16],设定飞行器近场成像几何模型参数,如表1所示。

表1 成像参数设定
结合表1,当雷达波中心频率为0.6 GHz时,补偿函数ΩⅠ(a,b,k,ξ)和ΩⅡ(a,b,k,ξ)对应的相位值如图3所示。由图3可知,在360°全孔径范围内,补偿函数ΩⅠ(a,b,k,ξ)和ΩⅡ(a,b,k,ξ)变化范围大,非线性特点明显,不利于进行泰勒级数展开或者高次函数拟合,因此针对ΩⅠ(a,b,k,ξ)和ΩⅡ(a,b,k,ξ)的精确补偿是困难的。相应地,一种直观的处理办法是通过子孔径处理限制相位误差,即设定子孔径宽度θsub(等同于成像积累角Θ),在子孔径内,如果相位补偿函数对应的相对误差小于π/4,则可以忽略相位补偿函数对成像的影响,并不再补偿。直观地理解,即是将斜距平面谱S(a,b,k,ξ)近似为水平面频谱Sg(a,b,k,ξ),从而忽略了频谱的投影处理。
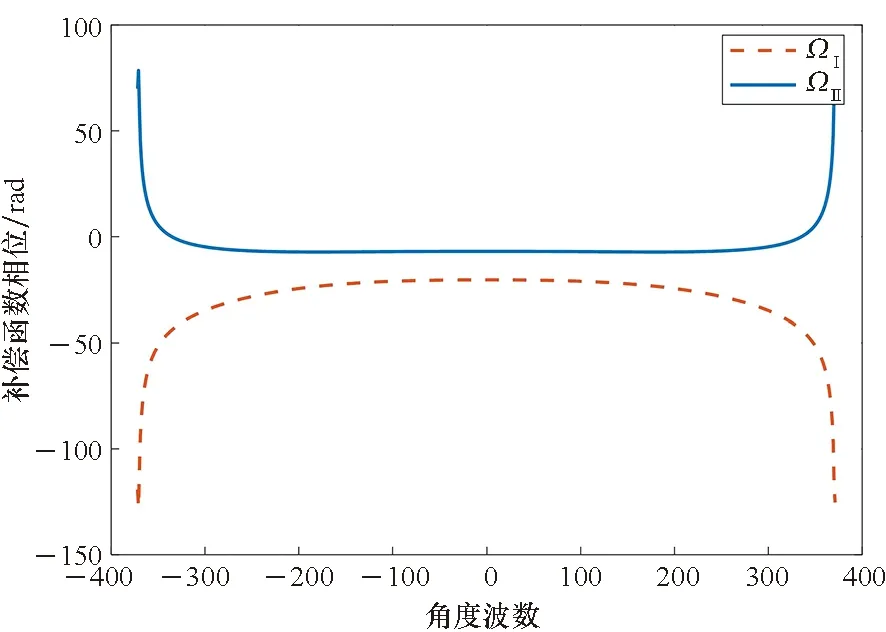
图3 补偿函数相位随角度波数的变化趋势Fig.3 Phase of compensation function variations according to angular wavenumber
以表1为基础,在0.6~35 GHz的频率范围内,以相位相对变化值不超过π/4为约束,可以得到不同频段条件下适合的子孔径宽度选定范围,如图4所示。图4中,横坐标为允许采用的子孔径宽度,纵坐标对应不同的雷达中心频率,图中黄色区域代表子孔径宽度的可行域。直观地,当雷达中心频率低时,所允许的子孔径宽度更大,当雷达中心频率增高,对应的子孔径宽度不断减小。
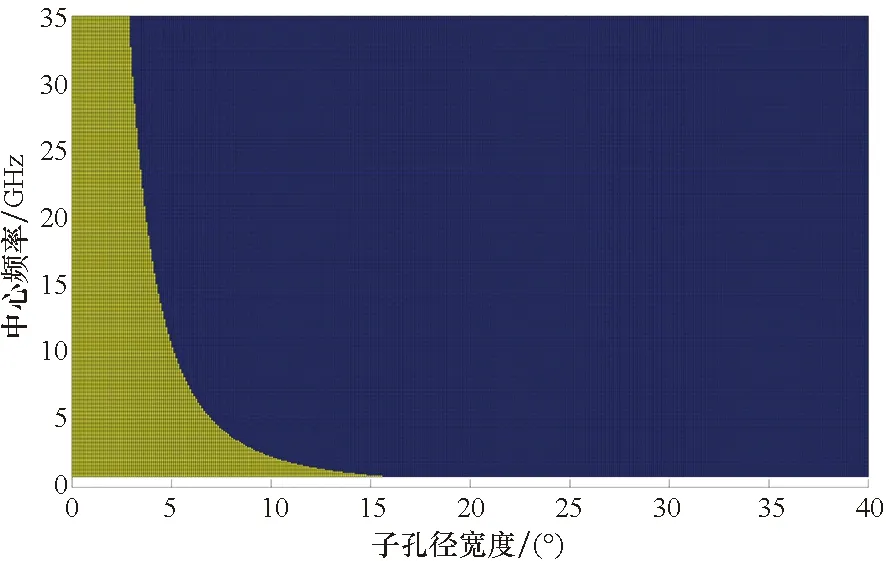
图4 针对不同频段可采用的子孔径频段宽度Fig.4 Acceptable width of sub-aperture according to different wavebands
基于上述处理思路形成本文的成像策略,即采用子孔径处理(等效为小转角)获得雷达图像,并通过处理一系列子孔径数据,评估飞行器全方位的散射特性。
2 频域算法处理流程
结合第1节的理论分析,总结得到近场频域处理流程如图5所示。
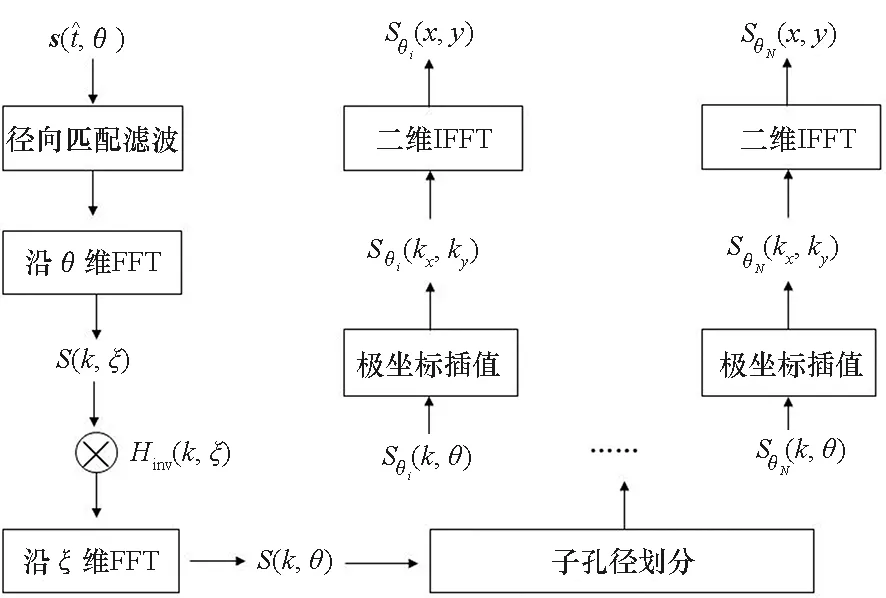
图5 本文算法的成像处理流程Fig.5 Imaging procedure of the proposed method
(13)
经Hinv(k,ξ)补偿后,式(12)演变得到:
S′g(R,r,k,ξ)
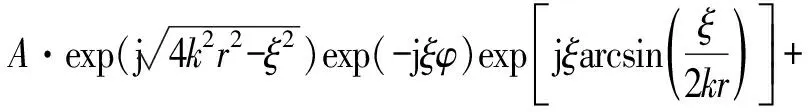
(14)
将S′g(R,r,k,ξ)关于ξ进行逆快速傅里叶变换(inverse fast Fourier transform, IFFT)[11],得到方位时域信号:
S(k,θ)=A·exp(j2krcosθZcosθcosφ)·
exp(j2krcosθZsinθsinφ)
(15)
对S(k,θ)进行子孔径划分,得到Sθi(k,θ),θi(i∈[1,N])对应不同的子孔径积累角(不同的转角区间);随后进行式(16)所示极坐标插值得到Sθi(kx,ky)=exp(jkxrcosφ)exp(jkyrsinφ);再经过二维IFFT得到子孔径图像;通过对序列子孔径图像的后续处理,可得到不同转角区间对应的飞行器近场成像结果。
(16)
值得特意说明的是,在实际的应用中,应考虑近场测量中天线方向图引起的锥削现象,否则将引入较大的幅值误差[17-18]。鉴于本文关注于高效精确成像算法,暂不涉及RCS外推与校正,因此文中的分析未考虑天线方向图的影响。
3 数值分析
在表1所示成像参数的基础上,设定如表2所示的典型成像参数,开展仿真数据的成像分析。
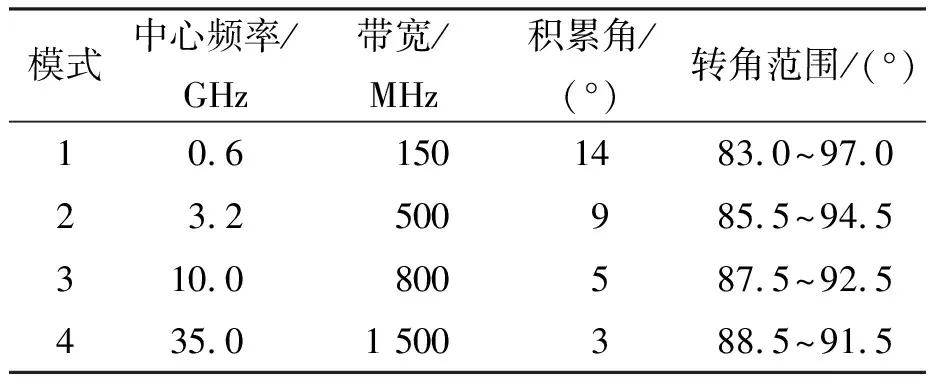
表2 典型成像参数设定
鉴于人们习惯于对径向与横向呈正交状态的图像进行评估,表2中4类模式的转角区间均以90°为中心,并采用PFA和BPA对比不同算法的成像结果。边缘散射点对应最大的成像半径。图6展示了模式1对应的成像结果,图6(a)表示利用本文算法处理得到的散射点成像结果;图6(b)对应PFA处理得到的成像结果;图6(c)代表图6(a)中边缘点(0 m,-15 m)对应的点散布函数分布;图6(d)为图6(a)中边缘点(0 m,-15 m)对应的BPA成像结果;图6(e)为图6(a)的频谱支撑域;图6(f)和(g)分别表示图6(c)所示点散布函数沿横向(Y)和径向(X)的剖面图。
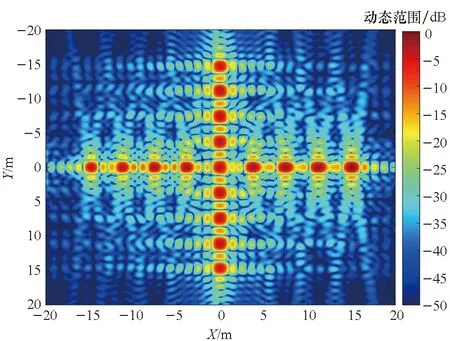
(a) 本文方法得到的结果(a) Result produced by the proposed algorithm
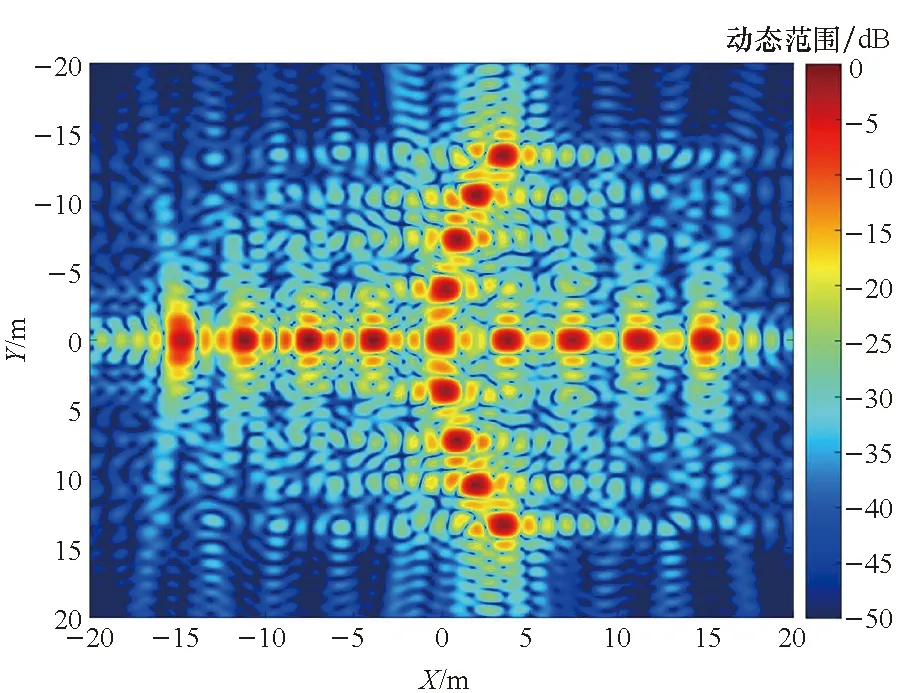
(b) PFA处理得到的成像结果(b) Imaging result produced by the PFA
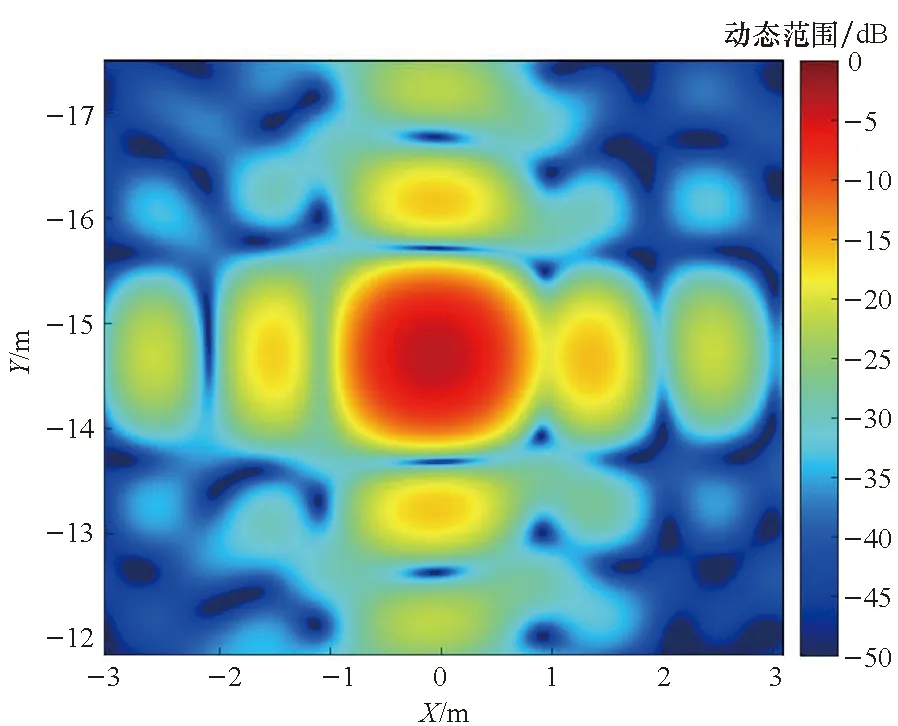
(c) 点目标成像结果的放大展示(c) Enlarged display of point target imaging result
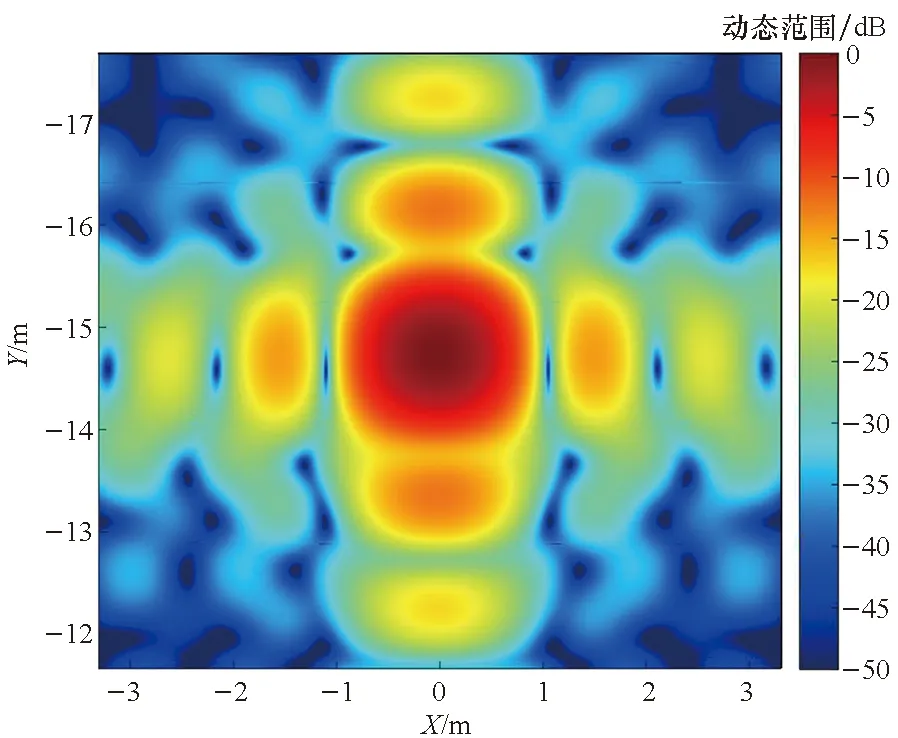
(d) 针对图6
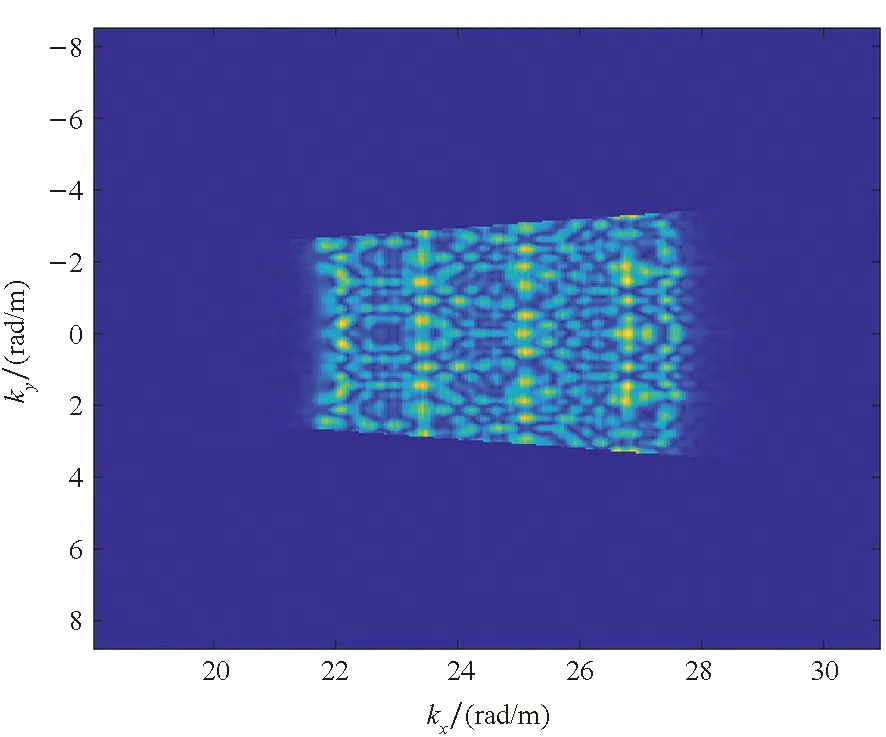
(e) 子孔径数据对应的频谱形状(e) Spectrum shape according to the sub-aperture data
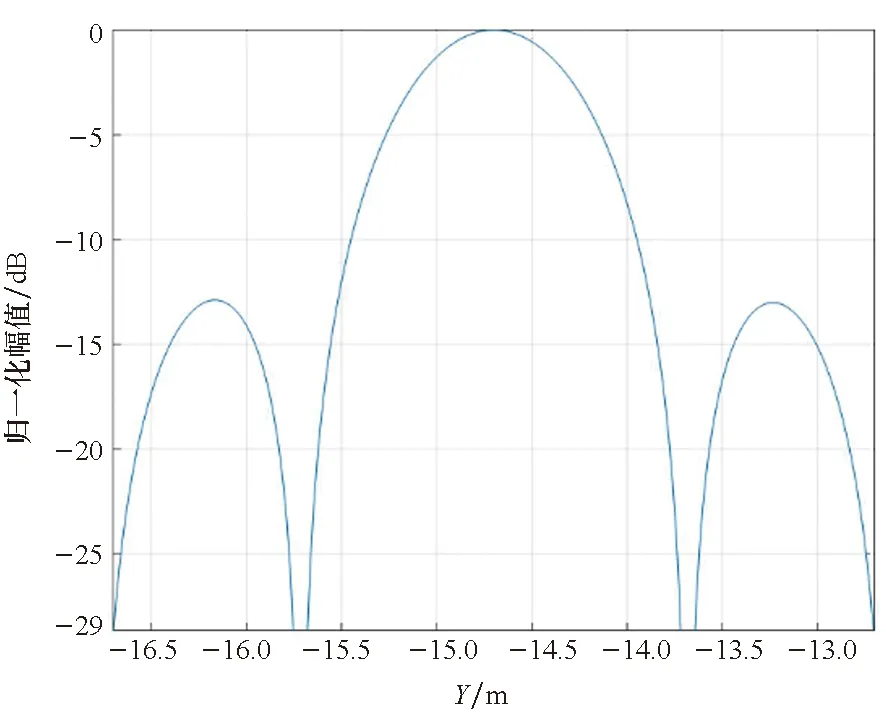
(f) 沿Y方向的剖面图(f) Profile in direction of Y
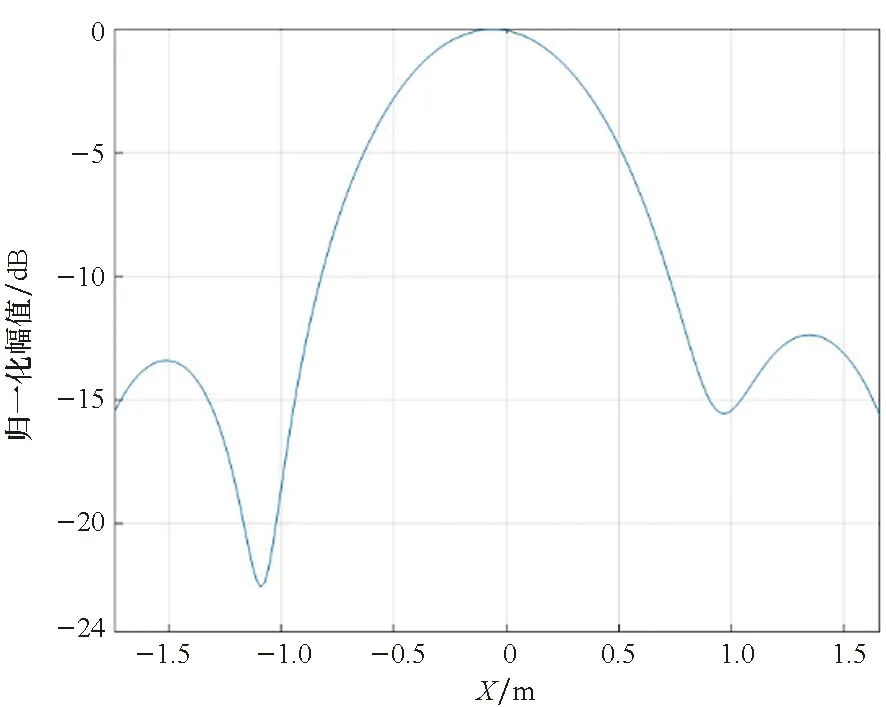
(g) 沿X方向的剖面图
类似地,图7、图8、图9分别展示了模式2、模式3、模式4对应的成像结果。
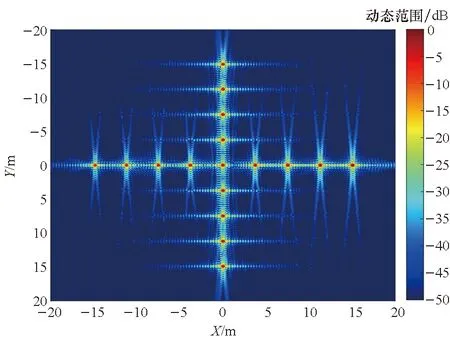
(a) 本文方法得到的结果(a) Result produced by the proposed algorithm
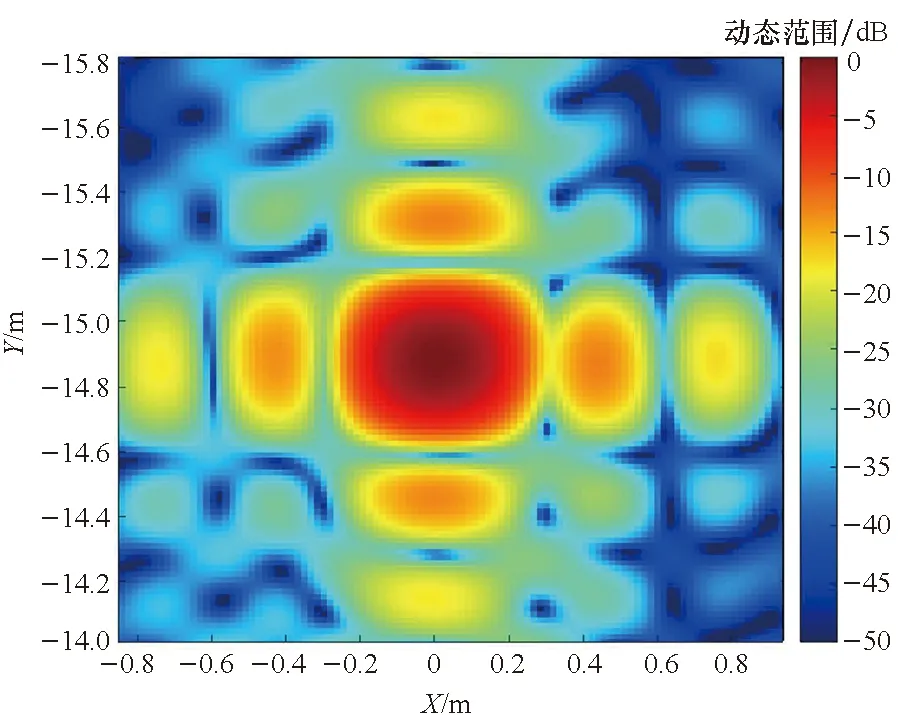
(b) 点目标成像结果的放大展示(b) Enlarged display of point target imaging result
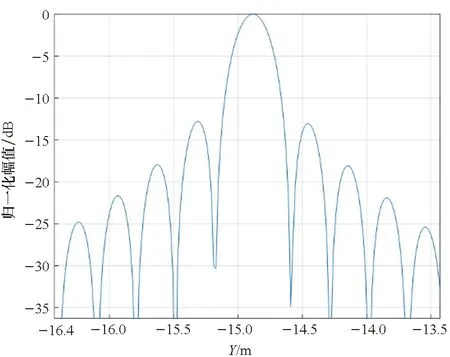
(c) 沿Y方向的剖面图(c) Profile in direction of Y
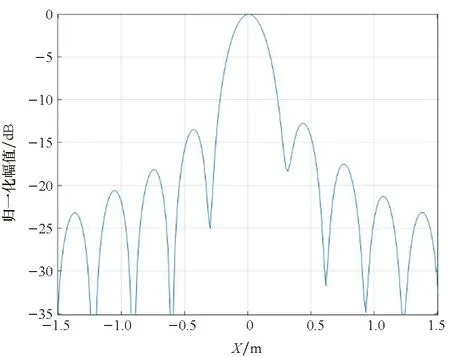
(d) 沿X方向的剖面图
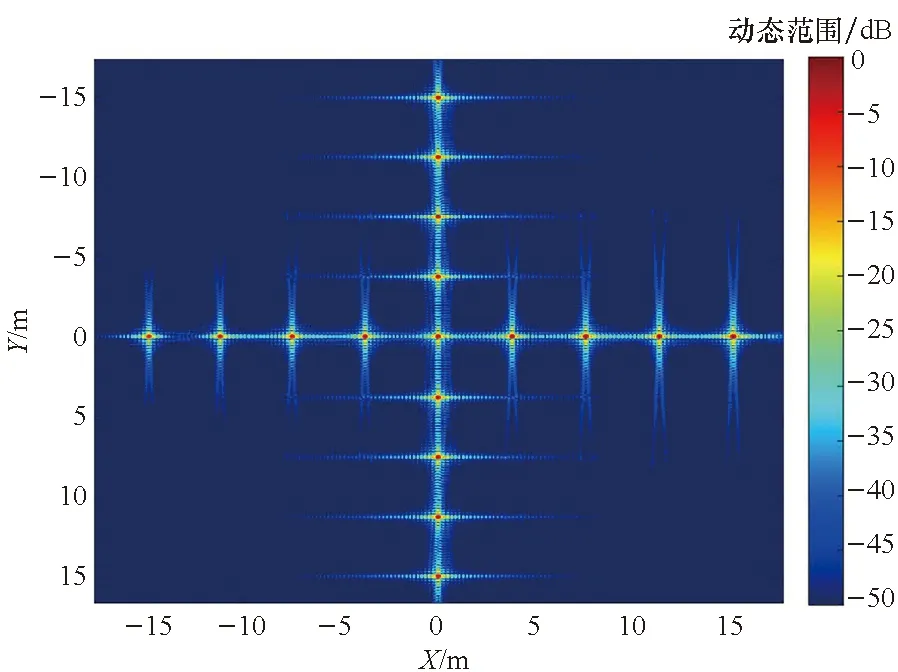
(a) 本文方法得到的结果(a) Result produced by the proposed algorithm
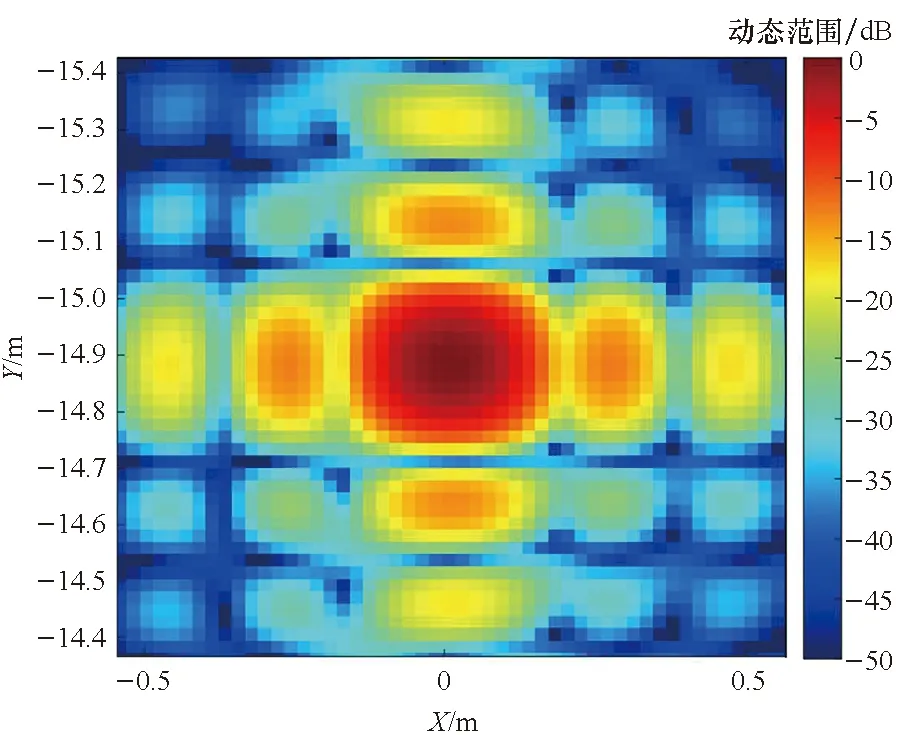
(b) 点目标成像结果的放大展示(b) Enlarged display of point target imaging result

(c) 沿Y方向的剖面图(c) Profile in direction of Y
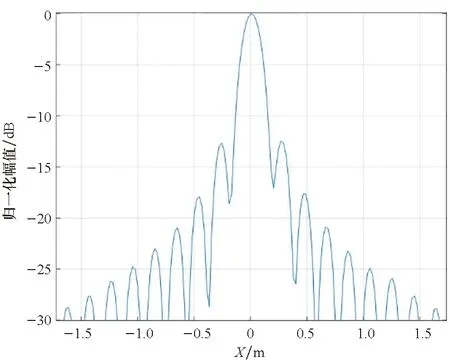
(d) 沿X方向的剖面图

(a) 本文方法得到的结果(a) Result produced by the proposed algorithm
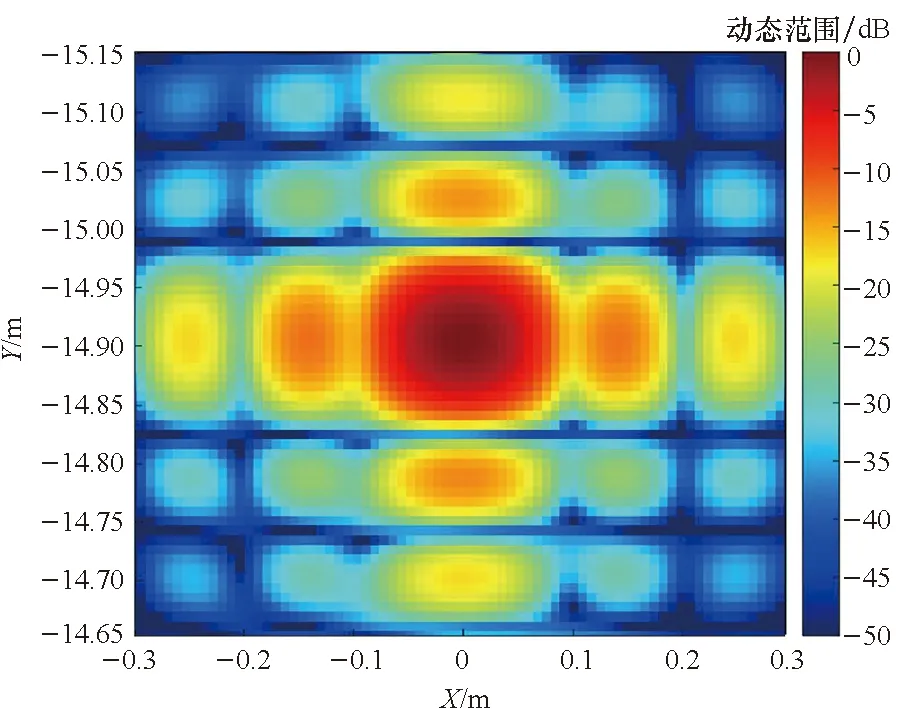
(b) 点目标成像结果的放大展示(b) Enlarged display of point target imaging result
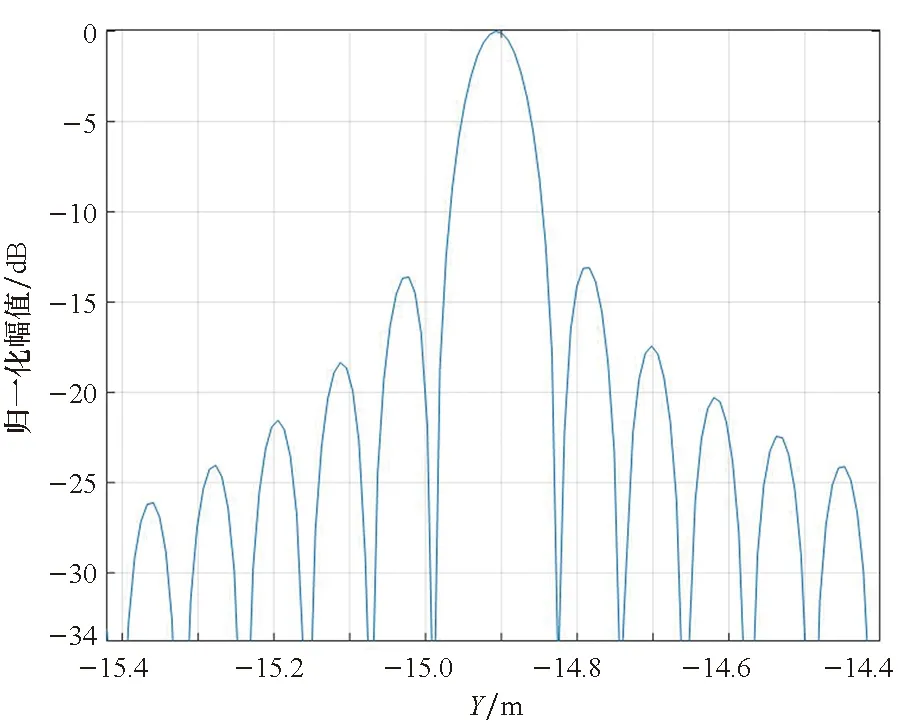
(c) 沿Y方向的剖面图(c) Profile in direction of Y
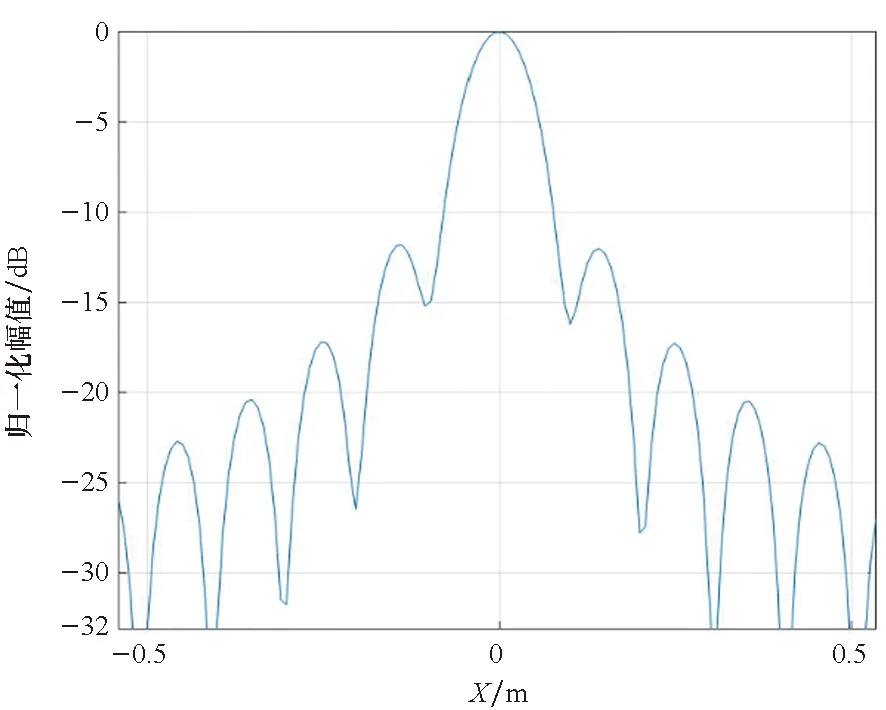
(d) 沿X方向的剖面图(d) Profile in direction of X图9 模式4对应成像结果Fig.9 Imaging results according to model 4
针对图6~9所示剖面图,统计分辨率、峰值旁瓣比等成像质量参数,如表3所示。
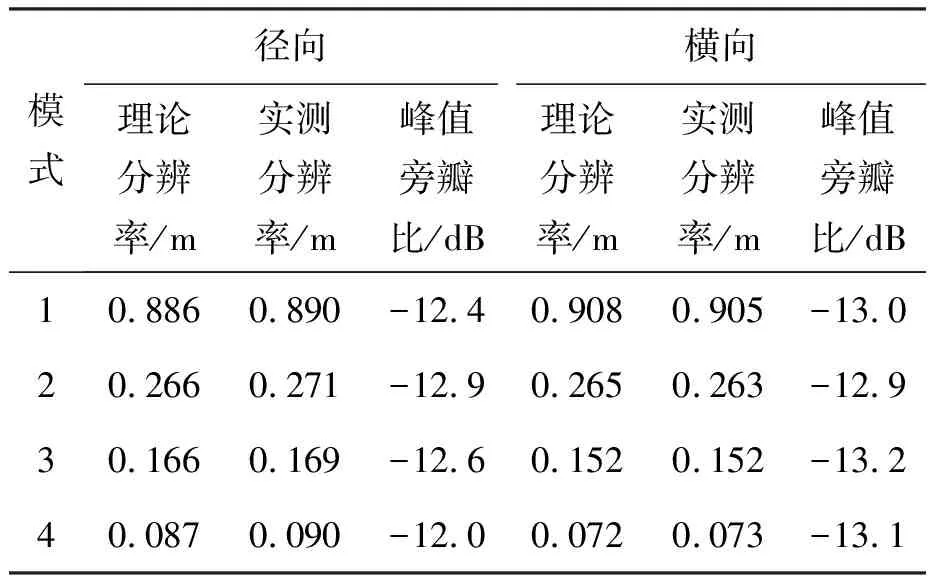
表3 成像结果的详细分析
由图6(a)与图6(b)对比可知,随着观测半径的增大,PFA成像质量下降,并存在明显的位置偏移,这同PFA需满足远场条件的前提是吻合的;由图6(c)和图6(d)对比可知,本文方法得到的成像结果与BPA基本一致;表3所示成像量化分析证实本文方法处理得到的成像结果同理论值吻合。仿真成像分析证实了成像流程的可行性和鲁棒性。
观察图6~9,总体上看,在子孔径成像策略下,点散布函数基本上是二维可分离的sinc函数,这从频谱支撑域的形状上也可以看出。但也应注意到有所差异:
首先,点散布函数的Y向剖面图中,右侧第一旁瓣略高,主瓣与第一旁瓣之间的谷峰电平较理想值高,该现象同采样间隔、插值精度、近似引入的相位误差以及频谱支撑域的形状是否为规则的矩形均相关,但图示结果在实际应用中是可接受的。
其次,在散射点的定位方面,与理想值之间存在较小的偏差,偏差的引入主要由插值处理造成且通常为固定偏差,当偏差值小于分辨率时可以忽略它的影响,也可以进行一致性的校正。
4 结论
结合全尺寸飞行器在室内或者室外较小区域进行雷达散射特征诊断的迫切需要,本文通过简要对比,分析了近场成像的特点,介绍了近场成像算法的研究现状。针对转台成像模型,以获得近场雷达图像为目的,建立了适用于飞行器电磁散射特征诊断的近场成像通用模型,分析了近场测量回波的频谱形式,理论上阐述了转台成像模式下频域成像处理的难点和挑战。针对近场转台成像的典型几何模型,本文基于散射点在较小角域范围内近似恒定的假设,提出了一种频域快速成像算法,并分别针对典型波段进行数值仿真分析。良好的成像质量证实了本文所提出的理论分析与成像算法的可行性。需要指出的是,本文的研究,侧重于成像聚焦质量和近场雷达图像的获取,未考虑天线方向图锥削效应的影响,以及RCS的标定与外推。
