高速铁路网络延误传播分析

王 璞,谭淮锐,郭 宝,周 慧

(中南大学 交通运输工程学院, 湖南 长沙 410075)

高速铁路列车的运行状态可能会受到多种因素(极端天气、设备故障、运营管理不当等)的影响,进而发生列车延误[1]。列车延误不仅会打乱列车运行计划,影响高速铁路的运营管理;而且会使乘客的出行受到影响,降低乘客的乘车满意度。对高速铁路列车延误进行分析研究,理解高速铁路网络中的延误传播机理,对于制定更为科学的列车运行计划、提高运营管理水平具有十分重要的理论和实际意义。下面首先介绍列车延误研究领域的相关研究工作。

根据列车延误发生原因的不同,列车延误可以分为初始延误和连带延误[2]。列车发生初始延误的主要因素包括天气因素、人为因素和系统性因素[3]。列车发生初始延误后,延误传播效应的存在会导致后续列车发生连带延误[4]。Meester等[5]建立了列车延误传播模型,并从列车初始延误的概率分布推导出连带延误的概率分布。胡思继等[6]研究了区段内列车延误传播过程和传播规律,定义了相关延误指标并推导出理论计算公式。庄河等[7]运用广铁集团管辖的6条高速铁路实绩数据建立了不同致因情况下初始延误时长分布模型。Wang等[8]识别了列车延误关键车站,并提出时间间隔阈值用于构建列车延误传播链,识别列车延误传播是否发生。柏赟等[9]考虑了不同运行线路的列车在运行线的交叉区域存在运行干扰的情况,并提出最优接近速度策略使受到延误传播影响的列车迅速通过运行干扰区域,尽快恢复正常运行。曾壹等[10]使用区间锁闭时间模型对列车延误区间增加和传播的范围进行预测,并提出列车节能-延误恢复模型,不仅可以降低列车牵引能耗,还能缓解列车的延误传播。

上述研究针对列车间的延误传播,其延误本因是铁路线路的连通性以及列车共用铁路线路的运行机制[1],所以列车间的延误传播会导致站点间的延误传播。为研究站点间的延误传播关系,Lessan等[11]运用武广高铁实绩运行数据构建了三种贝叶斯网络,发现基于数据驱动和领域专家知识的混合方法构建的贝叶斯网络在预测延误时间方面有更高的精度。Corman等[12]对瑞典铁路一段交通走廊线路中的站点延误传播关系进行了研究,并运用领域专家知识构建了贝叶斯网络。但这些研究都只关注单条铁路线路,而不是铁路网络。相较于某条铁路单线,铁路网络具有更复杂的拓扑结构,所以仅使用领域专家知识难以判别大型铁路网络中站点间的延误传播关系。因此,本文采用数据驱动方法构建高速铁路站点延误传播贝叶斯网络,并运用复杂网络中的渗流理论寻找并分析处于渗流突变状态下的延误传播团簇,以探究高速铁路网络中的延误传播机理。

1 站点延误传播贝叶斯网络模型

1.1 贝叶斯网络理论

贝叶斯网络是一种对因果关系进行推理的概率图模型[13],其中每个节点代表的随机变量可用于表达任何问题的抽象形式,由父节点指向子节点的有向边代表节点之间的相互依赖关系。若贝叶斯网络中存在n个节点(1,2,…,n),每个节点对应的随机变量为X1,X2,…,Xn,则其联合概率分布为

(1)

式中,p(Xj)代表Xj的父节点集合。

1.2 贝叶斯网络结构学习

在研究铁路单线中站点间的延误传播关系时,学者大多结合领域专家知识建立贝叶斯网络[11]。但是在研究大型高速铁路网络中站点间的延误传播关系时,复杂的网络拓扑结构使上述方法难以判别站点间的延误传播关系。本文通过采用NO TEARS贝叶斯网络结构学习算法将有向无环图的结构学习问题表示为一个纯连续优化问题,相较于传统启发式算法更加精准,可以学习到全局最优的贝叶斯网络[14]。贝叶斯网络的结构优化问题在数学上表示为以下形式:

s.t.h(W)=0

(2)

式中,W是给定数据集,F(W)是与数据有关的损失函数,h(W)是一个平滑函数。

对于此非凸优化问题,可以将上式中的无环约束表示为

h(W)=tr(W∘W)-d=0

(3)

式中,tr()表示求矩阵的迹,“∘ ”表示Hadamard积。h(W)的梯度值为

∇h(W)=(eW∘W)T∘ 2W

(4)

得到最终需要进行优化的数学表达式:

s.t.h(W)=0

(5)

式中:ρ是大于0的一个二次惩罚项,以表示惩罚违反约束h(W)=0。至此可以采用NO TEARS算法对问题进行求解,具体步骤如算法1所示。

算法1 NO TEARS算法

1.3 数据处理

通过分析2018年1月20日至3月20日的高速列车实绩运行数据和列车时刻表数据,得到高速列车延误信息,这些信息包括列车车次、日期、到达站点、图定到站时间、实际到站时间、延误时长(见表1)。考虑到海南省和台湾省高铁站点暂时未与其他省份高速铁路网络相连接,所以本文只将上述两者以外省份的高速铁路网络作为研究范围(共543个站点,481 523条列车延误信息)。

1.4 模型构建

将高速列车主要运行时段6:00—24:00分割为18个1 h的时间窗,研究时段内共有1 080个时间窗。通过式(6)计算各站点在各时间窗内所有延误列车的平均延误时长,最后将其整理为NO TEARS贝叶斯网络结构学习算法输入所需的数据矩阵形式,即1 080行、543列的站点平均延误时长矩阵T。

(6)

根据1.2节推导过程,建立高速铁路网络站点延误传播贝叶斯网络模型的目标函数和约束条件:

s.t.h(W)=0

(7)

进一步使用Python 3.8 集成环境Anaconda,同时应用NO TEARS贝叶斯网络结构学习算法对应的causalnex贝叶斯网络库建立高速铁路网络站点延误传播贝叶斯网络,并分别采用causalnex贝叶斯网络库、pympy贝叶斯网络库和Networkx复杂网络库中有向无环图检验模块对所建立的网络结构进行检验,结果显示所建立的贝叶斯网络均通过算法的有向无环图检验。模型结构示意如图1所示。

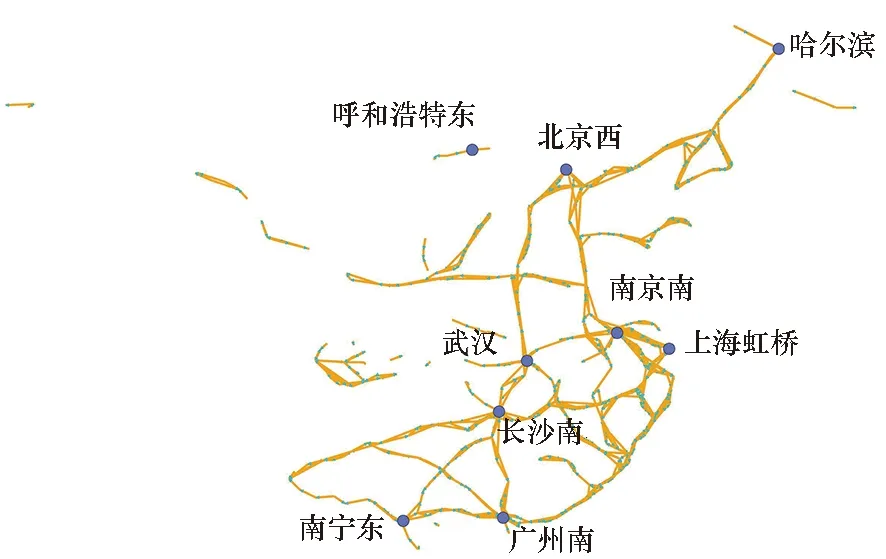
图1 站点延误传播贝叶斯网络示意图Fig.1 Schematic diagram of delay propagation Bayesian network

2 基于渗流理论的延误传播规律分析

在复杂网络中,渗流理论[15]描述了网络中节点或边被移除时,网络结构发生变化的过程。当网络中某一参数发生变化,网络会出现巨大团簇分裂成若干个小团簇的现象;参数变化到某一临界阈值(渗流阈值)时,网络性质会突然发生改变,这种突变称为渗流突变。

2.1 延误传播团簇演变分析

站点延误传播贝叶斯网络模型中边和边的权重由NO TEARS算法获取,模型中的边表示两个站点之间的延误传播关系,边权重wij越大表示父节点站点i对子节点站点j造成的延误传播影响越强。基于渗流理论和已构建的站点延误传播贝叶斯网络,本文设置不同的权重阈值q观察站点延误传播贝叶斯网络的演变情况[16]。对于给定的权重阈值q,站点延误传播贝叶斯网络中各条边根据权重wij被划分为有效边(eij=1)和无效边(eij=0),如式(8)所示。网络中的站点通过有效边相互连接形成团簇,同一团簇中的站点存在有效边互相连接,不同团簇中的站点之间没有边相连。所以在给定权重阈值q下,根据不同团簇之间是否存在有效边连接,网络被划分为多个不同大小的延误传播团簇。

(8)

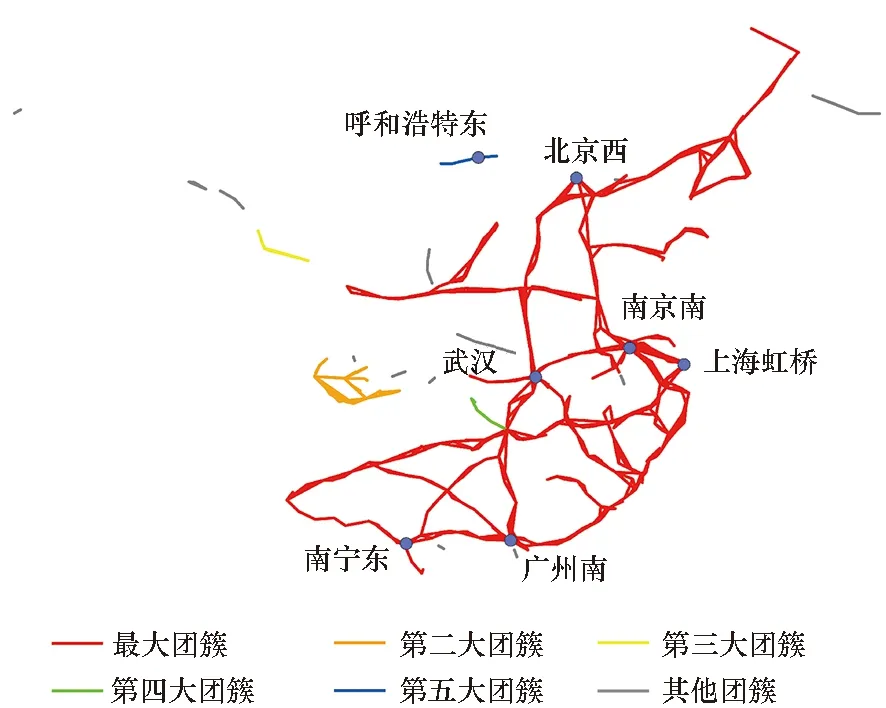
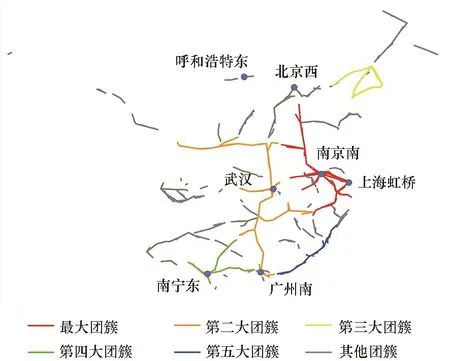
随着权重阈值q的变化,网络发生渗流突变过程。为了展示网络的渗流突变过程,图2展示了在不同权重阈值下网络中延误传播团簇的地理位置分布情况(分别选取小于、等于和大于渗流临界权重阈值的权重q=0.2、q=0.35、q=0.6)。结合图3中不同权重阈值下的延误传播团簇规模可以看出,随着权重阈值q逐渐增大,站点延误传播贝叶斯网络中最大延误传播团簇不断变小,而第二大延误传播团簇规模呈现震荡变大的趋势;当权重阈值q增加到渗流临界权重阈值qc时,第二大延误传播团簇的规模达到峰值,而最大延误传播团簇突然瓦解,此时站点延误传播贝叶斯网络处于渗流突变状态[15];当权重阈值q大于渗流临界权重阈值qc时,整体网络继续瓦解,直至网络全部解体。

(a) q=0.2

(b) q=0.35

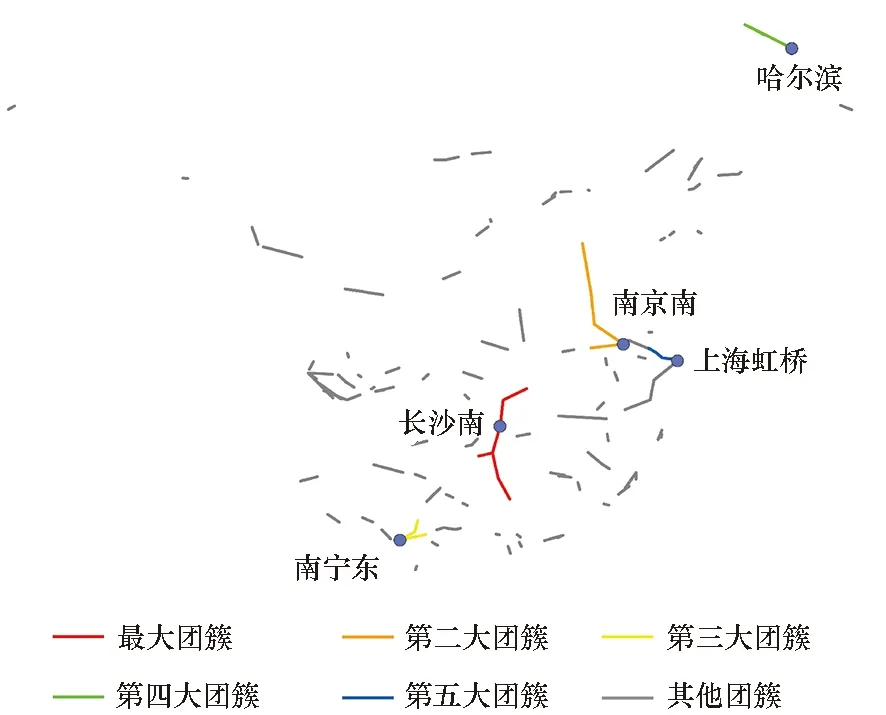
(c) q=0.6图2 不同权重阈值q下延误传播团簇的地理位置Fig.2 Delay propagation clusters′ locations under different weight threshold q values

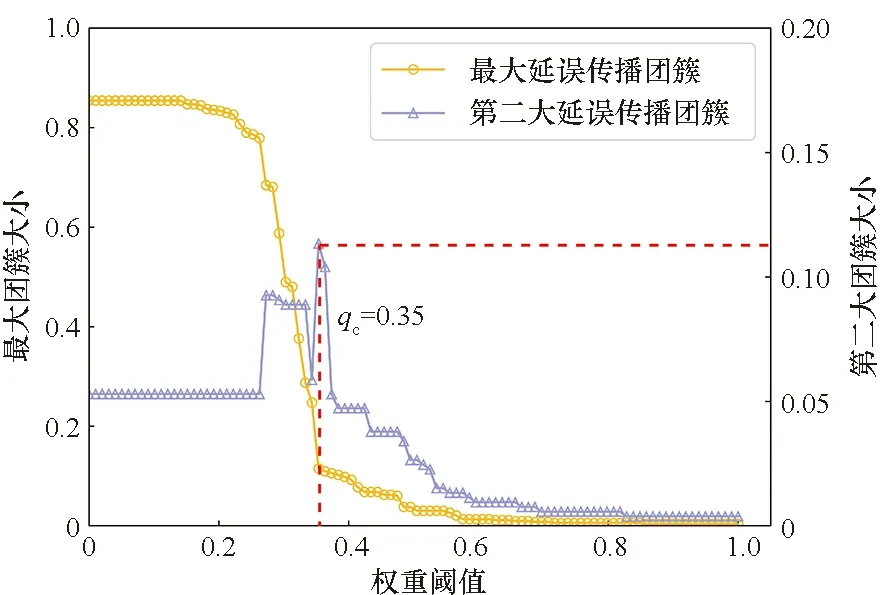
图3 不同权重阈值q下延误传播团簇规模Fig.3 Size of delay propagation clusters under different weight threshold q values

2.2 渗流突变状态下的网络分析

在渗流理论中,网络突变十分关键。Wu等[16]通过分析权重阈值等于渗流阈值的网络结构,发现核心团簇可以以较少的边展现原网络的骨架结构,体现出原网络的核心特征。在其他多数研究中[17-20]也将网络的权重阈值设置为渗流阈值,进而对网络中的核心团簇进行分析,从复杂的网络结构中寻找到重要的边。本节为寻找到网络中重要的延误传播关系,揭示网络中延误传播的核心特征,进一步分析图2(b)中渗流突变状态下站点延误传播贝叶斯网络形成的核心延误传播团簇(qc=0.35)。

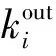
站点延误传播贝叶斯网络模型以有向边连接具有延误传播关系的两个站点,因此,在延误传播团簇中,根据站点的出度和入度,可将站点划分为3类:

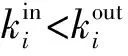
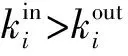
南京南站在最大延误传播团簇内被划分为延误发散站点。图4展示了南京南站产生的延误传播链,从图中可以看出南京南站可以首先将延误传播至附近的合肥南站、蚌埠南站等站点,而合肥南站、蚌埠南站可以进一步将延误分别传播至六安站、徐州东站等站点;在延误传播的过程中,湖州站、徐州东站、济南西站等延误发散站点具有多条延误传播链,进而可以在多方向将延误传播至浙江、河北等与南京南站相距较远地区的站点。这种延误传播模式使大部分延误发散站点成为延误传播中心(如图4中南京南站、济南西站、徐州东站等站点),将延误“辐射式”传播至其他站点。

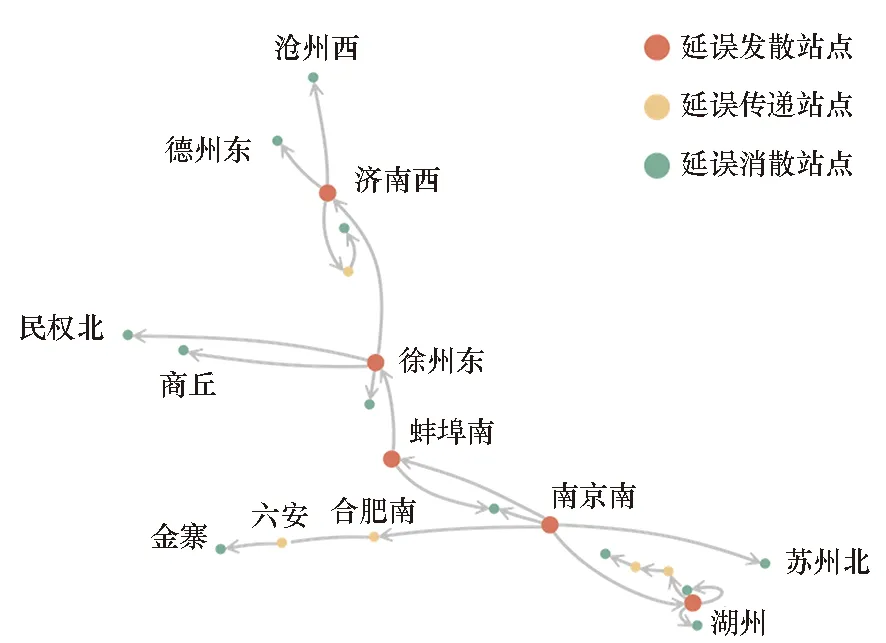
图4 南京南站产生的延误传播链Fig.4 Delay propagation chain generated by Nanjingnan Railway Station

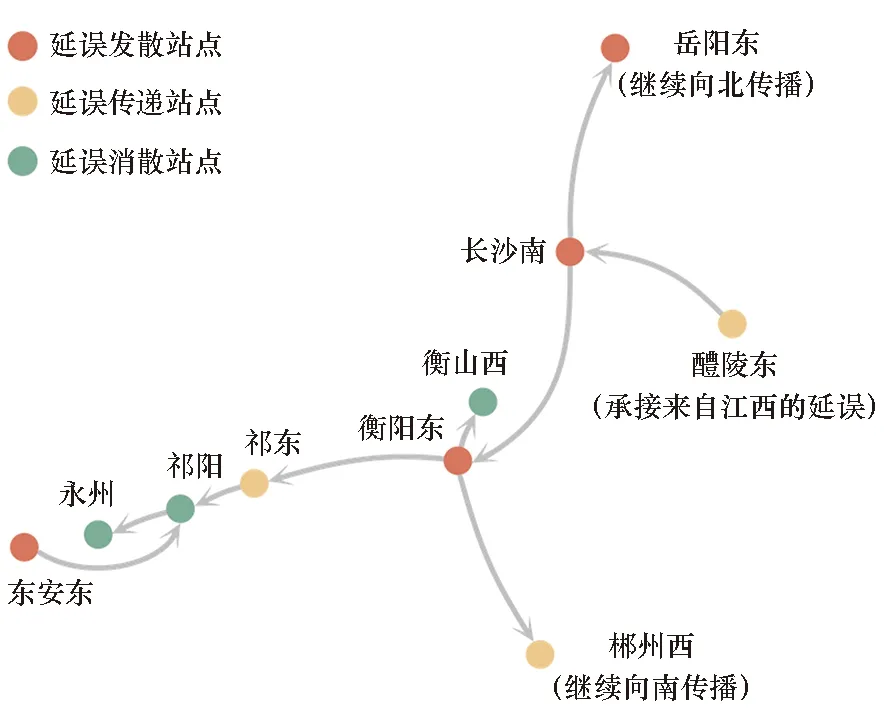
图5 长沙南站产生的延误传播链Fig.5 Delay propagation chain generated by Changshanan Railway Station

其他延误传播团簇具有相似的延误传播规律。以第二大延误传播团簇为例,图5展现了湖南地区的站点延误传播规律,可以看出湖南地区延误传播以长沙南站和衡阳东站这类延误发散站点为延误传播中心,将延误以延误传播链的形式“辐射式”传播至其他站点。其中长沙南站向北可以将延误经岳阳东站继续传播至湖北地区,向南可以传播至衡阳东站;而衡阳东站也具有多条延误传播链,可以将延误传播至祁东站、郴州西站等站点,进而传播至永州和广东地区,向网络继续扩散延误。

为从定量的角度分析网络中的延误传播规律,本文进一步分析了受到延误发散站点延误传播影响的站点数量变化情况。在延误传播的过程中,如果站点j受到站点i延误传播影响,那么存在一条从站点i至站点j的传播路径满足以下要求:延误由站点i开始,随着时间窗的推移,其路径上的站点沿传播路径方向依次发生延误。

图6展示了2018年3月15日网络中受到长沙南站延误传播影响的站点数量变化情况。从图中可以看出:在15:00—18:00时间段,延误处于初始传播阶段,此时新增的延误站点数量不断增加,延误站点减少数量一直为0,致使此时段内每一时间窗的延误站点数量和累计延误站点总数急剧升高。在18:00—21:00时间段,新增的延误站点数量和延误站点减少数量接近平衡,所以各时间窗的延误站点数量基本维持不变;但由于新增的站点数仍然保持在较高值,所以累计延误站点总数仍然急剧升高。在21:00—23:00时间段,由于大部分延误的高速列车在晚间结束全天的运行,延误在网络中扩散被阻碍,所以新增的延误站点数量逐步减少而延误站点总数继续增长,大部分站点从延误状态逐步恢复为正常状态。

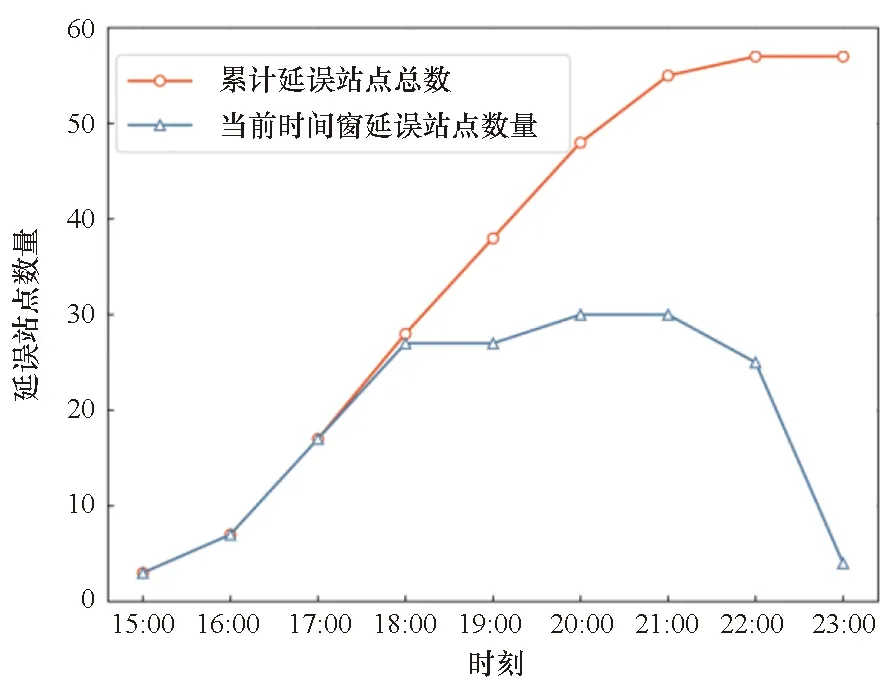
(a) 延误站点数量变化(a) The number of delayed stations

(b) 延误站点增减数量变化(b) Changes of the number of delayed stations 图6 受延误传播影响的站点数量Fig.6 The number of stations affected by delay propagation

3 站点延误状态预测

3.1 预测模型建立

基于渗流突变状态下站点延误传播贝叶斯网络中的核心延误传播团簇,对高速铁路站点延误状态进行预测。为预测下一时间窗目标站点的延误状态,在站点延误状态预测模型中不仅考虑了目标站点的父节点站点延误状态,而且加入了两站点间的列车运行信息,以捕捉延误随列车运行传播到站点的动态变化情况。用于预测站点延误状态的贝叶斯网络模型结构如图7所示(在本图的案例中,待预测站点有两个父节点),其中模型变量集确定如下:

Y={S1j,…,Snj,SAj+1,Z1j+1,…,Znj+1}

式中,SAj+1为待预测站点A在j+1时间窗的延误状态,Snj为站点A的第n个父节点站点在j时间窗的延误状态。中国铁路总公司将小于等于4 min的列车到站晚点视为可被车站运营组织管理所吸收的晚点,不会对列车和车站造成大的影响[22]。因此根据式(9)将站点的延误状态划分为延误状态Sij=1和非延误状态Sij=0。

(9)

式中,Sij为i站点在j时间窗的延误状态,Tij为i站点在j时间窗的列车平均延误时长。

Znj+1表示在j+1时间窗内,站点A的第n个父节点站点与站点A之间是否有列车运行。因为两站点间并不是在所有时段内都会有高速列车运行,所以在预测站点延误状态时加入两站点间的列车运行信息Znj+1,以捕捉列车的运行动态变化情况。Znj+1根据列车时刻表数据和j时间窗的列车运行信息得到,取值为{1,0},其中1表示两站点间有高速列车运行,0表示无高速列车运行。

3.2 预测结果分析

将60天数据集划分为模型的训练集和测试集,以数据集前70%时段即2018年1月20日至2018年3月2日的数据作为模型的训练集,以数据集后30%时段即2018年3月3日至2018年3月20日的数据作为模型的测试集。预测准确率R(计算见式(10))为89.56%,表明基于核心延误传播团簇的预测模型很好地捕捉了网络中核心的延误传播关系。

(10)

式中,N为预测样本数,ytrue为正确预测站点是否处于延误状态的样本数。

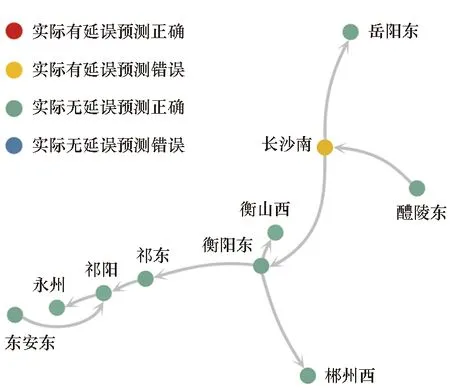
(a) 14:00预测结果(a) Prediction result at 14:00

(b) 15:00预测结果(b) Prediction result at 15:00

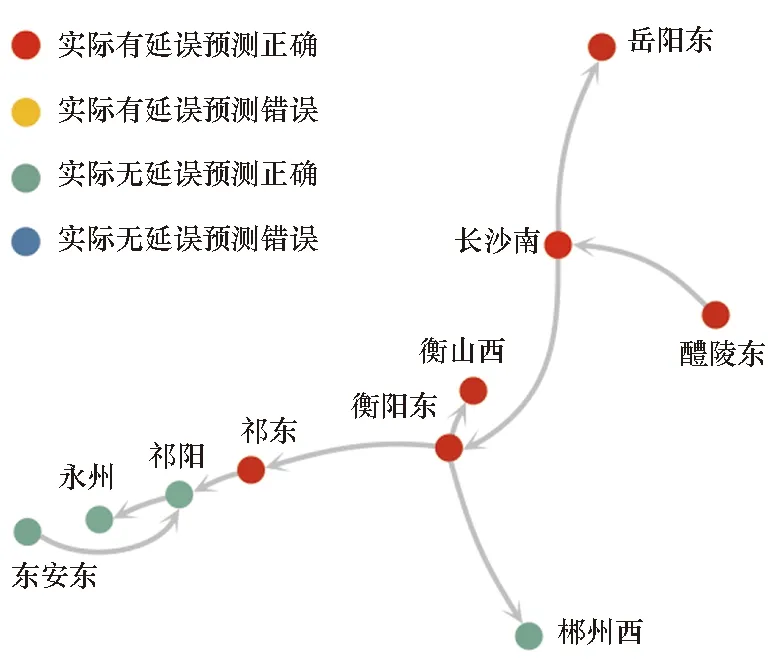
(c) 16:00预测结果(c) Prediction result at 16:00

(d) 17:00预测结果(d) Prediction result at 17:00图8 湖南地区预测结果示例Fig.8 Example prediction result in Hunan province

为进一步说明模型的预测结果和网络中的延误传播规律,选取2018年3月15日的实际案例,对延误在网络中大范围传播的动态过程进行分析。图8展示了延误首先发生在长沙南站逐步传播至湖南地区的动态变化情况和模型的预测结果。从图中可以看出,14:00湖南地区长沙南站首先处于延误状态,附近的其他站点此时都处于非延误状态;随着时间的推移,15:00长沙南站的延误已经传播到了岳阳东站、衡阳东站,进而形成多条延误传播链,在后续时段内将延误传播至郴州西站、衡山西站等更多站点;直到17:00,湖南地区大部分站点都处于延误状态。预测模型虽然未能捕捉到14:00长沙南站产生的突发性延误,但能够精准地预测延误的动态传播趋势,对于网络中站点延误预警有着重要意义。

4 结论

本文建立了高速铁路网络的站点延误传播贝叶斯网络模型,并结合渗流理论对高速铁路网络延误传播规律进行研究,主要得到以下结论:随着权重阈值q增大,站点延误传播贝叶斯网络中最大延误传播团簇不断减小,而第二大延误传播团簇在渗流临界权重阈值qc时达到最大;从延误传播的角度将站点划分成延误发散站点、延误传递站点和延误消散站点,其中延误发散站点产生的延误传播链使网络以部分延误发散站点为延误中心向延误传递站点和延误消散站点进行“辐射式”延误传播。在预测站点延误状态方面,由于延误传播团簇很好地捕捉了网络中核心的延误传播关系,能够用于站点延误状态预警。

研究结果可以帮助管理者从全局性视角理解延误在网络中的传播机理,进而制定更高效的高速铁路行车组织管理方案,以防止延误从局部网络向全网扩散。未来可在现有基础上融合多源数据更深层次地分析站点发生延误的原因,并结合专家领域知识提升模型预测精度。